Focus on Fluids
On the microhydrodynamics of superspreading
-
- Published online by Cambridge University Press:
- 22 February 2011, pp. 1-4
-
- Article
-
- You have access
- Export citation
Papers
On surfactant-enhanced spreading and superspreading of liquid drops on solid surfaces
-
- Published online by Cambridge University Press:
- 25 January 2011, pp. 5-37
-
- Article
- Export citation
Buoyancy-driven instabilities of miscible two-layer stratifications in porous media and Hele-Shaw cells
-
- Published online by Cambridge University Press:
- 31 January 2011, pp. 38-65
-
- Article
- Export citation
The formation and evolution of stratification during transient mixing ventilation
-
- Published online by Cambridge University Press:
- 31 January 2011, pp. 66-84
-
- Article
- Export citation
Steady vortex dipoles with general profile functions
-
- Published online by Cambridge University Press:
- 07 February 2011, pp. 85-95
-
- Article
- Export citation
Takens–Bogdanov bifurcation of travelling-wave solutions in pipe flow
-
- Published online by Cambridge University Press:
- 25 January 2011, pp. 96-129
-
- Article
- Export citation
Non-normality and its consequences in active control of thermoacoustic instabilities
-
- Published online by Cambridge University Press:
- 22 February 2011, pp. 130-149
-
- Article
- Export citation
Particle dispersion by random waves in the rotating Boussinesq system
-
- Published online by Cambridge University Press:
- 12 January 2011, pp. 150-175
-
- Article
- Export citation
Direct numerical simulation of turbulence in injection-driven three-dimensional cylindrical flows
-
- Published online by Cambridge University Press:
- 19 January 2011, pp. 176-203
-
- Article
- Export citation
Variations on Kolmogorov flow: turbulent energy dissipation and mean flow profiles
-
- Published online by Cambridge University Press:
- 22 February 2011, pp. 204-213
-
- Article
- Export citation
An experimental study of the effect of external turbulence on the decay of a single vortex and a vortex pair
-
- Published online by Cambridge University Press:
- 22 February 2011, pp. 214-239
-
- Article
- Export citation
Pulsatile jets
-
- Published online by Cambridge University Press:
- 12 January 2011, pp. 240-259
-
- Article
- Export citation
Break-away separation for high turbulence intensity and large Reynolds number
-
- Published online by Cambridge University Press:
- 22 February 2011, pp. 260-300
-
- Article
- Export citation
Vorticity inversion and action-at-a-distance instability in stably stratified shear flow
-
- Published online by Cambridge University Press:
- 14 January 2011, pp. 301-325
-
- Article
- Export citation
Deformation of a flexible polymer in a random flow with long correlation time
-
- Published online by Cambridge University Press:
- 07 February 2011, pp. 326-336
-
- Article
- Export citation
Flow-induced degradation of drag-reducing polymer solutions within a high-Reynolds-number turbulent boundary layer
-
- Published online by Cambridge University Press:
- 22 February 2011, pp. 337-364
-
- Article
- Export citation
Cross-independence closure for statistical mechanics of fluid turbulence
-
- Published online by Cambridge University Press:
- 26 January 2011, pp. 365-403
-
- Article
- Export citation
Hamiltonian form of the modified nonlinear Schrödinger equation for gravity waves on arbitrary depth
-
- Published online by Cambridge University Press:
- 26 January 2011, pp. 404-426
-
- Article
- Export citation
Universal size and shape of viscous capillary jets: application to gas-focused microjets
-
- Published online by Cambridge University Press:
- 22 February 2011, pp. 427-438
-
- Article
- Export citation
Atwood ratio dependence of Richtmyer–Meshkov flows under reshock conditions using large-eddy simulations
-
- Published online by Cambridge University Press:
- 01 February 2011, pp. 439-480
-
- Article
- Export citation


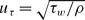 , based on the shear stress derived from the sum of the mean and the root mean square, i.e.
, based on the shear stress derived from the sum of the mean and the root mean square, i.e. 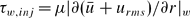 , is proposed for the scaling of turbulent viscosity for turbulent flows with strong injection. We also show that the mean streamwise velocity profile has an inflection point near the injecting surface.
, is proposed for the scaling of turbulent viscosity for turbulent flows with strong injection. We also show that the mean streamwise velocity profile has an inflection point near the injecting surface.