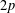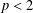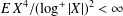507 results in 60Exx
COMPLETE CONVERGENCE FOR ARRAYS AND THE LAW OF THE SINGLE LOGARITHM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 29 August 2017, pp. 333-344
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
On the range of the transient frog model on ℤ
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 26 June 2017, pp. 327-343
- Print publication:
- June 2017
-
- Article
- Export citation
New maximal inequalities for N-demimartingales with scan statistic applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 22 June 2017, pp. 363-378
- Print publication:
- June 2017
-
- Article
- Export citation
Large deviations of means of heavy-tailed random variables with finite moments of all orders
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 66-81
- Print publication:
- March 2017
-
- Article
- Export citation
Stochastic comparisons of interfailure times under a relevation replacement policy
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 134-145
- Print publication:
- March 2017
-
- Article
- Export citation
Corrected discrete approximations for the conditional and unconditional distributions of the continuous scan statistic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 304-319
- Print publication:
- March 2017
-
- Article
- Export citation
Comparison of time-inhomogeneous Markov processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 11 January 2017, pp. 1015-1044
- Print publication:
- December 2016
-
- Article
- Export citation
Improved Chen‒Stein bounds on the probability of a union
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1265-1270
- Print publication:
- December 2016
-
- Article
- Export citation
Order statistics with memory: a model with reliability applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 974-988
- Print publication:
- December 2016
-
- Article
- Export citation
On the double Laplace transform of the truncated variation of a Brownian motion with drift
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 October 2016, pp. 281-292
-
- Article
-
- You have access
- Export citation
One-component regular variation and graphical modeling of extremes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 733-746
- Print publication:
- September 2016
-
- Article
- Export citation
Compound geometric approximation under a failure rate constraint
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 700-714
- Print publication:
- September 2016
-
- Article
- Export citation
Approximating the Laplace transform of the sum of dependent lognormals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 203-215
- Print publication:
- July 2016
-
- Article
- Export citation
A direct approach to the stable distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 261-282
- Print publication:
- July 2016
-
- Article
- Export citation
Stable laws and Beurling kernels
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 239-248
- Print publication:
- July 2016
-
- Article
- Export citation
On comparing coherent systems with heterogeneous components
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 88-111
- Print publication:
- March 2016
-
- Article
- Export citation
Correlated fractional counting processes on a finite-time interval
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1045-1061
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
On the singular components of a copula
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1175-1182
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Erratum to: Mixture representations of residual lifetimes of used systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1183-1186
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
On dynamic mutual information for bivariate lifetimes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 1157-1174
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation