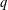507 results in 60Exx
On perpetuities with gamma-like tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 368-389
- Print publication:
- June 2018
-
- Article
- Export citation
Stochastic comparisons of coherent systems under different random environments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 459-472
- Print publication:
- June 2018
-
- Article
- Export citation
On unimodality of the lifetime distribution of coherent systems with failure-dependent component lifetimes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 473-487
- Print publication:
- June 2018
-
- Article
- Export citation
On the significands of uniform random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 353-367
- Print publication:
- June 2018
-
- Article
- Export citation
On the age of a randomly picked individual in a linear birth-and-death process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 82-93
- Print publication:
- March 2018
-
- Article
- Export citation
On stochastic comparisons of k-out-of-n systems with Weibull components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 216-232
- Print publication:
- March 2018
-
- Article
- Export citation
A remark on positive sojourn times of symmetric processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 69-81
- Print publication:
- March 2018
-
- Article
- Export citation
On multivariate records from random vectors with independent components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 43-53
- Print publication:
- March 2018
-
- Article
- Export citation
Univariate and multivariate stochastic comparisons and ageing properties of the generalized Pólya process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 233-253
- Print publication:
- March 2018
-
- Article
- Export citation
Domains of attraction for positive and discrete tempered stable distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 30-42
- Print publication:
- March 2018
-
- Article
- Export citation
FURTHER RESULTS ON QUANTILE ENTROPY IN THE PAST LIFETIME
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 33 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 27 February 2018, pp. 146-159
-
- Article
- Export citation
COMPARISON OF WEAK AND STRONG MOMENTS FOR VECTORS WITH INDEPENDENT COORDINATES
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 211-229
- Print publication:
- 2018
-
- Article
- Export citation
A necessary and sufficient condition for the subexponentiality of the product convolution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 57-73
- Print publication:
- March 2018
-
- Article
- Export citation
On sequences of expected maxima and expected ranges
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1144-1166
- Print publication:
- December 2017
-
- Article
- Export citation
PRESERVATION OF LOG-CONCAVITY UNDER CONVOLUTION
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 32 / Issue 4 / October 2018
- Published online by Cambridge University Press:
- 26 September 2017, pp. 567-579
-
- Article
- Export citation
Stochastic comparison of parallel systems with heterogeneous exponential components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 970-976
- Print publication:
- September 2017
-
- Article
- Export citation
Excursion sets of infinitely divisible random fields with convolution equivalent Lévy measure
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 833-851
- Print publication:
- September 2017
-
- Article
- Export citation
Almost stochastic dominance under inconsistent utility and loss functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 763-772
- Print publication:
- September 2017
-
- Article
- Export citation
Taylor's law, via ratios, for some distributions with infinite mean
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 657-669
- Print publication:
- September 2017
-
- Article
- Export citation
Increasing convex order on generalized aggregation of SAI random variables with applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 685-700
- Print publication:
- September 2017
-
- Article
- Export citation