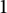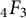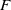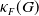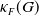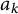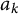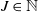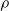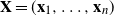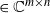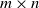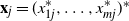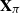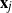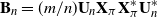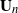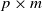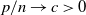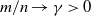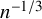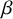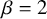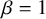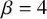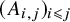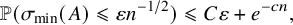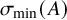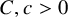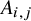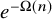171 results in 60Bxx
Moments of the free Jacobi process: A matrix approach
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 10 March 2025, pp. 1-26
-
- Article
- Export citation
Edge Statistics for Lozenge Tilings of Polygons, II: Airy Line Ensemble
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOUNDED CONJUGACY CLASSES AND CONJUGACY CLASSES SUPPORTING INVARIANT MEASURES AND AUTOMORPHISMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 February 2025, pp. 1-6
-
- Article
- Export citation
Large N limit of the Yang–Mills measure on compact surfaces II: Makeenko–Migdal equations and the planar master field
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 January 2025, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal linear sofic approximations of countable groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 24 January 2025, pp. 245-268
- Print publication:
- May 2025
-
- Article
- Export citation
Mean field limits of co-evolutionary signed heterogeneous networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 06 January 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Central Limit Theorem for tensor products of free variables
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 December 2024, pp. 1-33
-
- Article
-
- You have access
- HTML
- Export citation
Gaussian fluctuations for the two-urn model
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STABILITY ANALYSIS FOR STOCHASTIC MCKEAN–VLASOV EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal , First View
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1-13
-
- Article
-
- You have access
- HTML
- Export citation
Cokernel statistics for walk matrices of directed and weighted random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 18 October 2024, pp. 131-150
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partial recovery and weak consistency in the non-uniform hypergraph stochastic block model
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 09 October 2024, pp. 1-51
-
- Article
-
- You have access
- HTML
- Export citation
The full rank condition for sparse random matrices
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 20 September 2024, pp. 643-707
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The limiting spectral distribution of large random permutation matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1301-1318
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Asymptotic expansions relating to the distribution of the length of longest increasing subsequences
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 March 2024, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THERMODYNAMIC FORMALISM FOR AMENABLE GROUPS AND COUNTABLE STATE SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 2647-2711
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic expansion of
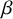 $\beta $ matrix models in the multi-cut regime
$\beta $ matrix models in the multi-cut regime
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 24 January 2024, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The least singular value of a random symmetric matrix
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 23 January 2024, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Max-linear graphical models with heavy-tailed factors on trees of transitive tournaments
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 621-665
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
Local convergence of critical Galton–Watson trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 30 November 2023, pp. 851-857
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
From topological recursion to wave functions and PDEs quantizing hyperelliptic curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 October 2023, e99
-
- Article
-
- You have access
- Open access
- HTML
- Export citation