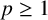1. Introduction
McKean–Vlasov stochastic differential equations (SDEs), originating from the seminal works [Reference McKean15, Reference Vlasov18], are also known as mean-field SDEs or distribution-dependent SDEs which are used to study the interacting particle system and mean-field games. There are numerous works on the well-posedness, ergodicity and large deviations [Reference Hong, Li and Liu10, Reference Liu and Ma13, Reference Reis, Salkeld and Tugaut17, Reference Wang19]. Moreover, there are also several works on the stability of the McKean–Vlasov SDEs. Recently, Ding and Qiao [Reference Ding and Qiao5] considered the stability for the McKean–Vlasov SDEs with non-Lipschitz coefficients
 $$ \begin{align} dX(t)&=b(X(t),\mathcal{L}(X(t)))\,dt+\sigma(X(t),\mathcal{L}(X(t)))\,dW(t),\nonumber\\ X(0)&=x_{0}, \end{align} $$
$$ \begin{align} dX(t)&=b(X(t),\mathcal{L}(X(t)))\,dt+\sigma(X(t),\mathcal{L}(X(t)))\,dW(t),\nonumber\\ X(0)&=x_{0}, \end{align} $$
where
![]() $\mathcal {L}(X(t))$
is the distribution of
$\mathcal {L}(X(t))$
is the distribution of
![]() $X(t)$
,
$X(t)$
,
![]() $W_{\cdot }=(W^{1}_{\cdot },W^{2}_{\cdot },\dots ,W^{l}_{\cdot })$
is a
$W_{\cdot }=(W^{1}_{\cdot },W^{2}_{\cdot },\dots ,W^{l}_{\cdot })$
is a
![]() $\mathcal {F}_{t}$
-adapted standard Brownian motion and the coefficients
$\mathcal {F}_{t}$
-adapted standard Brownian motion and the coefficients
![]() $b: \mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{2}}(\mathbb {R}^{d})\to \mathbb {R}^{d}$
and
$b: \mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{2}}(\mathbb {R}^{d})\to \mathbb {R}^{d}$
and
![]() $\sigma : \mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{2}}(\mathbb {R}^{d})\to \mathbb {R}^{d}\times \mathbb {R}^{l}$
are Borel measurable functions. The definition of
$\sigma : \mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{2}}(\mathbb {R}^{d})\to \mathbb {R}^{d}\times \mathbb {R}^{l}$
are Borel measurable functions. The definition of
![]() $\mathcal {M}_{\lambda ^{2}}(\mathbb {R}^{d})$
is defined in the next section. Sufficient conditions are given for the exponential stability of the second moments for their solutions in terms of a Lyapunov function [Reference Khasminskii12]. Furthermore, the almost surely (a.s.) asymptotic stability of their solutions is also discussed. Lv and Shan [Reference Lv and Shan14] considered the long time behaviour of stochastic McKean–Vlasov equations, and the exponential and logarithmic decay are discussed. Bahlali et al. [Reference Bahlali, Mezerdi and Mezerdi1] discussed the existence and uniqueness of solutions under a non-Lipschitz condition and derived various stability properties with respect to initial data, coefficients and driving processes. Wu et al. [Reference Wu, Hu, Gao and Yuan20] studied the stability of solutions of McKean–Vlasov SDEs via feedback control based on discrete-time state observation and derived the
$\mathcal {M}_{\lambda ^{2}}(\mathbb {R}^{d})$
is defined in the next section. Sufficient conditions are given for the exponential stability of the second moments for their solutions in terms of a Lyapunov function [Reference Khasminskii12]. Furthermore, the almost surely (a.s.) asymptotic stability of their solutions is also discussed. Lv and Shan [Reference Lv and Shan14] considered the long time behaviour of stochastic McKean–Vlasov equations, and the exponential and logarithmic decay are discussed. Bahlali et al. [Reference Bahlali, Mezerdi and Mezerdi1] discussed the existence and uniqueness of solutions under a non-Lipschitz condition and derived various stability properties with respect to initial data, coefficients and driving processes. Wu et al. [Reference Wu, Hu, Gao and Yuan20] studied the stability of solutions of McKean–Vlasov SDEs via feedback control based on discrete-time state observation and derived the
![]() $\mathrm {H}_{\infty }$
stability, asymptotic stability and exponential stability in mean square for the controlled systems.
$\mathrm {H}_{\infty }$
stability, asymptotic stability and exponential stability in mean square for the controlled systems.
In this paper, we first provide a sufficient condition for the pth moment exponential stability and a.s. exponential stability for (1.1) (Theorem 3.2) by using the classical Lyapunov function method. Furthermore, asymptotic stability in distribution is derived by introducing a distribution-dependent operator, together with a similar discussion as that for SDE with Markovian switching [Reference Yuan and Mao21].
There are many recent works on the stability in distribution for stochastic differential equations with distribution-independent coefficients. Yuan et al. [Reference Yuan, Zou and Mao22] discussed the stochastic differential equations with Markovian switching and investigated the stability in distribution of the equations. Further, Du et al. [Reference Du, Dang and Dieu6] improved the result of Yuan et al. [Reference Yuan, Zou and Mao22] by giving a new sufficient condition for stability in distribution. Bao et al. [Reference Bao, Hou and Yuan2] considered a neutral stochastic differential delay equation with Markovian switching and obtained sufficient conditions for stability in distribution. Fei et al. [Reference Fei, Fei, Deng and Mao8] considered the stability in distribution for a highly nonlinear stochastic differential equation driven by G-Brownian motion [Reference Peng16].
The rest of the paper is organized as follows. In Section 2, we recall some preliminary knowledge. The pth moment exponential stability and a.s. exponential stability is presented in Section 3.1. The stability in distribution is established in Section 3.2.
2. Preliminary and main result
Let
![]() $C(\mathbb {R}^{d})$
be the collection of continuous functions on
$C(\mathbb {R}^{d})$
be the collection of continuous functions on
![]() $\mathbb {R}^{d}$
. For convenience, we denote the norm of vectors and matrices by
$\mathbb {R}^{d}$
. For convenience, we denote the norm of vectors and matrices by
![]() $|\cdot |$
and
$|\cdot |$
and
![]() $\|\cdot \|$
, respectively. Furthermore, let
$\|\cdot \|$
, respectively. Furthermore, let
![]() $\langle \cdot ,\cdot \rangle $
denote the scalar product in
$\langle \cdot ,\cdot \rangle $
denote the scalar product in
![]() $\mathbb {R}^{d}$
. Let
$\mathbb {R}^{d}$
. Let
![]() $\mathcal {B}(\mathbb {R}^{d})$
be the Borel
$\mathcal {B}(\mathbb {R}^{d})$
be the Borel
![]() $\sigma $
-algebra on
$\sigma $
-algebra on
![]() $\mathbb {R}^{d}$
and
$\mathbb {R}^{d}$
and
![]() $\mathcal {P}(\mathbb {R}^{d})$
denote the space of all probability measures defined on
$\mathcal {P}(\mathbb {R}^{d})$
denote the space of all probability measures defined on
![]() $\mathcal {B}(\mathbb {R}^{d})$
with the topology of weak convergence.
$\mathcal {B}(\mathbb {R}^{d})$
with the topology of weak convergence.
For
![]() $\lambda (x)=1+|x|$
,
$\lambda (x)=1+|x|$
,
![]() $x\in \mathbb {R}^d$
, define the Banach space
$x\in \mathbb {R}^d$
, define the Banach space
 $$ \begin{align*} C_{\lambda}(\mathbb{R}^{d})=\bigg\{\phi\in C(\mathbb{R}^{d})\bigg| \|\phi\|_{C_{\lambda}(\mathbb{R}^{d})}=\sup_{x\in \mathbb{R}^{d}}\frac{|\phi(x)|}{\lambda^2(x)}+\sup_{x\neq y}\frac{|\phi(x)-\phi(y)|}{|x-y|}<\infty\bigg\}. \end{align*} $$
$$ \begin{align*} C_{\lambda}(\mathbb{R}^{d})=\bigg\{\phi\in C(\mathbb{R}^{d})\bigg| \|\phi\|_{C_{\lambda}(\mathbb{R}^{d})}=\sup_{x\in \mathbb{R}^{d}}\frac{|\phi(x)|}{\lambda^2(x)}+\sup_{x\neq y}\frac{|\phi(x)-\phi(y)|}{|x-y|}<\infty\bigg\}. \end{align*} $$
Let
![]() $\mathcal {M}_{\lambda ^{p}}^{s}(\mathbb {R}^{d})$
be the space of signed measures m on
$\mathcal {M}_{\lambda ^{p}}^{s}(\mathbb {R}^{d})$
be the space of signed measures m on
![]() $\mathcal {B}(\mathbb {R}^{d})$
satisfying
$\mathcal {B}(\mathbb {R}^{d})$
satisfying
where
![]() $|m|=m^{+}+m^{-}$
, and
$|m|=m^{+}+m^{-}$
, and
![]() $m=m^{+}-m^{-}$
is the Jordan decomposition of m. Let
$m=m^{+}-m^{-}$
is the Jordan decomposition of m. Let
![]() $\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})=\mathcal {M}_{\lambda ^{p}}^{s}(\mathbb {R}^{d})\cap \mathcal {P}(\mathbb {R}^{d})$
be the set of probability measures on
$\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})=\mathcal {M}_{\lambda ^{p}}^{s}(\mathbb {R}^{d})\cap \mathcal {P}(\mathbb {R}^{d})$
be the set of probability measures on
![]() $\mathcal {B}(\mathbb {R}^{d})$
with finite pth moments equipped with the metric,
$\mathcal {B}(\mathbb {R}^{d})$
with finite pth moments equipped with the metric,
 $$ \begin{align*} \rho(\mu,\nu)\triangleq\sup_{\|\phi\|_{C_{\lambda}(\mathbb{R}^{d})}\leq1}\bigg|\!\int_{\mathbb{R}^{d}}\phi(x)\mu(dx)-\int_{\mathbb{R}^{d}}\phi(x)\nu(dx)\bigg|. \end{align*} $$
$$ \begin{align*} \rho(\mu,\nu)\triangleq\sup_{\|\phi\|_{C_{\lambda}(\mathbb{R}^{d})}\leq1}\bigg|\!\int_{\mathbb{R}^{d}}\phi(x)\mu(dx)-\int_{\mathbb{R}^{d}}\phi(x)\nu(dx)\bigg|. \end{align*} $$
Then,
![]() $(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}),\rho )$
is a complete metric space.
$(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}),\rho )$
is a complete metric space.
Given a complete filtered probability space
![]() $(\Omega , \mathcal {F}, \{\mathcal {F}_{t}\}_{t\in [0,\infty )},\mathbb {P})$
, we recall the definition of the derivative for a function with respect to a probability measure [Reference Cardaliaguet4]. A function
$(\Omega , \mathcal {F}, \{\mathcal {F}_{t}\}_{t\in [0,\infty )},\mathbb {P})$
, we recall the definition of the derivative for a function with respect to a probability measure [Reference Cardaliaguet4]. A function
![]() $f: \mathcal {M}_{\lambda ^{p}}^{s}(\mathbb {R}^{d})\to \mathbb {R}$
is differential at
$f: \mathcal {M}_{\lambda ^{p}}^{s}(\mathbb {R}^{d})\to \mathbb {R}$
is differential at
![]() $\mu \in \mathcal {M}_{\lambda ^{p}}^{s}(\mathbb {R}^{d})$
if for
$\mu \in \mathcal {M}_{\lambda ^{p}}^{s}(\mathbb {R}^{d})$
if for
![]() $\tilde {f}(\xi )\triangleq f(\mathbb {P}_{\xi }), \xi \in L^{p}(\Omega; \mathbb {R}^{d})$
, there exists some
$\tilde {f}(\xi )\triangleq f(\mathbb {P}_{\xi }), \xi \in L^{p}(\Omega; \mathbb {R}^{d})$
, there exists some
![]() $\zeta \in L^{p}(\Omega; \mathbb {R}^{d})$
with
$\zeta \in L^{p}(\Omega; \mathbb {R}^{d})$
with
![]() $\mathbb {P}_{\zeta }=\mu $
such that
$\mathbb {P}_{\zeta }=\mu $
such that
![]() $\tilde {f}$
is the Fréchet differential at
$\tilde {f}$
is the Fréchet differential at
![]() $\zeta $
, that is, there exists a linear continuous mapping
$\zeta $
, that is, there exists a linear continuous mapping
![]() $D\tilde {f}(\zeta ): L^{p}(\Omega; \mathbb {R}^{d})\to \mathbb {R}$
such that for all
$D\tilde {f}(\zeta ): L^{p}(\Omega; \mathbb {R}^{d})\to \mathbb {R}$
such that for all
![]() $\eta \in L^{p}(\Omega; \mathbb {R}^{d})$
,
$\eta \in L^{p}(\Omega; \mathbb {R}^{d})$
,
Since
![]() $D\tilde {f}(\zeta )\in L(L^{p}(\Omega; \mathbb {R}^{d}),\mathbb {R})$
, by the Riesz representation theorem [Reference Brezis3], there exists a
$D\tilde {f}(\zeta )\in L(L^{p}(\Omega; \mathbb {R}^{d}),\mathbb {R})$
, by the Riesz representation theorem [Reference Brezis3], there exists a
![]() $\mathbb {P}$
-a.s. unique random variable
$\mathbb {P}$
-a.s. unique random variable
![]() $\mathcal {\theta }\in L^{p}(\Omega; \mathbb {R}^{d})$
such that for
$\mathcal {\theta }\in L^{p}(\Omega; \mathbb {R}^{d})$
such that for
![]() $\eta \in L^{p}(\Omega; \mathbb {R}^{d})$
,
$\eta \in L^{p}(\Omega; \mathbb {R}^{d})$
,
Thus, there exists a Borel measurable function
![]() $h: \mathbb {R}^{d}\to \mathbb {R}^{d}$
which depends on the distribution
$h: \mathbb {R}^{d}\to \mathbb {R}^{d}$
which depends on the distribution
![]() $\mathbb {P}_{\zeta }$
rather than
$\mathbb {P}_{\zeta }$
rather than
![]() $\zeta $
itself such that
$\zeta $
itself such that
![]() $\mathcal {\theta }=h(\zeta )$
, and for
$\mathcal {\theta }=h(\zeta )$
, and for
![]() $\xi \in L^{2}(\Omega; \mathbb {R}^{d})$
,
$\xi \in L^{2}(\Omega; \mathbb {R}^{d})$
,
We call
![]() $\partial _{\mu }f(\mathbb {P}_{\zeta })(y)\triangleq h(y), y\in \mathbb {R}^{d}$
as the derivative of
$\partial _{\mu }f(\mathbb {P}_{\zeta })(y)\triangleq h(y), y\in \mathbb {R}^{d}$
as the derivative of
![]() $f: \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})\to \mathbb {R}$
at
$f: \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})\to \mathbb {R}$
at
![]() $\mathbb {P}_{\zeta }, \zeta \in L^{p}(\Omega; \mathbb {R}^{d})$
.
$\mathbb {P}_{\zeta }, \zeta \in L^{p}(\Omega; \mathbb {R}^{d})$
.
Definition 2.1. Function f is said to be in
![]() $C^{1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
if for each
$C^{1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
if for each
![]() $\xi \in L^{2}(\Omega; \mathbb {R}^{d})$
, there exists a
$\xi \in L^{2}(\Omega; \mathbb {R}^{d})$
, there exists a
![]() $\mathbb {P}_{\xi }$
-modification of
$\mathbb {P}_{\xi }$
-modification of
![]() $\partial _{\mu }f(\mathbb {P}_{\zeta })(\cdot )$
which is denoted by
$\partial _{\mu }f(\mathbb {P}_{\zeta })(\cdot )$
which is denoted by
![]() $\partial _{\mu }f(\mathbb {P}_{\zeta })(\cdot )$
again, such that
$\partial _{\mu }f(\mathbb {P}_{\zeta })(\cdot )$
again, such that
![]() $\partial _{\mu }f: \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})\times \mathbb {R}^{d}\to \mathbb {R}^{d}$
is continuous and we identify the function
$\partial _{\mu }f: \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})\times \mathbb {R}^{d}\to \mathbb {R}^{d}$
is continuous and we identify the function
![]() $\partial _{\mu }f$
with the derivative of f.
$\partial _{\mu }f$
with the derivative of f.
Definition 2.2. A function f belongs to
![]() $C_{b}^{1,1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
if
$C_{b}^{1,1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
if
![]() $f\in C^{1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
, and
$f\in C^{1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
, and
![]() $\partial _{\mu }f$
is bounded and Lipschitz continuous, that is there exists a real number
$\partial _{\mu }f$
is bounded and Lipschitz continuous, that is there exists a real number
![]() $C>0$
such that:
$C>0$
such that:
-
(i)
 $\partial _{\mu }f(\mu )(x)|\leq C,\ \mu \in \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})$
;
$\partial _{\mu }f(\mu )(x)|\leq C,\ \mu \in \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})$
; -
(ii)
 $\partial _{\mu }f(\mu )(x)-\partial _{\mu }f(\nu )(y)|\leq C(\rho (\mu ,\nu )+|x-y|), \ \mu ,\nu \in \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}) $
$\partial _{\mu }f(\mu )(x)-\partial _{\mu }f(\nu )(y)|\leq C(\rho (\mu ,\nu )+|x-y|), \ \mu ,\nu \in \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}) $
for
![]() $x,y\in \mathbb {R}^{d}.$
$x,y\in \mathbb {R}^{d}.$
Definition 2.3. The function f is said to be in
![]() $C^{2}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
if for every
$C^{2}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
if for every
![]() $\mu \in \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})$
,
$\mu \in \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})$
,
![]() $f\in C^{1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
and
$f\in C^{1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
and
![]() $\partial _{\mu }f(\mathbb {P}_{\xi })(\cdot )$
is differentiable and its derivative
$\partial _{\mu }f(\mathbb {P}_{\xi })(\cdot )$
is differentiable and its derivative
![]() $\partial _{y}\partial _{\mu }f: \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})\times \mathbb {R}^{d}\to \mathbb {R}^{d}\times \mathbb {R}^{d}$
is continuous.
$\partial _{y}\partial _{\mu }f: \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})\times \mathbb {R}^{d}\to \mathbb {R}^{d}\times \mathbb {R}^{d}$
is continuous.
Definition 2.4. The function f is said to be in
![]() $C_{b}^{2,1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
if
$C_{b}^{2,1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
if
![]() $f\in C^{2}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))\cap C_{b}^{1,1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
and its derivative
$f\in C^{2}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))\cap C_{b}^{1,1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
and its derivative
![]() $\partial _{y}\partial _{\mu }f$
is bounded and continuous.
$\partial _{y}\partial _{\mu }f$
is bounded and continuous.
Definition 2.5. The function
![]() $\Phi \in C_{b}^{2,2,1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})\times \mathbb {R}^{d})$
if:
$\Phi \in C_{b}^{2,2,1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})\times \mathbb {R}^{d})$
if:
-
(i)
 $\Phi $
is bi-continuous with respect to
$\Phi $
is bi-continuous with respect to
 $(x,\mu )$
;
$(x,\mu )$
; -
(ii) for any x,
 $\Phi (x,\cdot )\in C_{b}^{2,1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
and for any
$\Phi (x,\cdot )\in C_{b}^{2,1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
and for any
 $\mu \in \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})$
,
$\mu \in \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})$
,
 $\Phi (\cdot ,\mu )\in C^{2}(\mathbb {R}^{d})$
.
$\Phi (\cdot ,\mu )\in C^{2}(\mathbb {R}^{d})$
.
If
![]() $\Phi \in C_{b}^{2,2,1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}\times \mathbb {R}^{d}))$
and
$\Phi \in C_{b}^{2,2,1}(\mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}\times \mathbb {R}^{d}))$
and
![]() $\Phi \geq 0$
, then we say
$\Phi \geq 0$
, then we say
![]() $\Phi \in C_{b+}^{2,2,1}(\mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
.
$\Phi \in C_{b+}^{2,2,1}(\mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
.
Definition 2.6. The function
![]() $\Phi \in \mathcal {C}(\mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
, if
$\Phi \in \mathcal {C}(\mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
, if
![]() $\Phi \in C^{2,2}(\mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
and for every compact set
$\Phi \in C^{2,2}(\mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
and for every compact set
![]() $K\subseteq \mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})$
,
$K\subseteq \mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})$
,
 $$ \begin{align*} \sup_{(x,\mu)\in K}\int_{\mathbb{R}^{d}}(\|\partial_{y}\partial_{\mu}\Phi(x,\mu)(y)\|^{2}+|\partial_{\mu}\Phi(x,\mu)(y)|^{2})\mu(dy)<\infty. \end{align*} $$
$$ \begin{align*} \sup_{(x,\mu)\in K}\int_{\mathbb{R}^{d}}(\|\partial_{y}\partial_{\mu}\Phi(x,\mu)(y)\|^{2}+|\partial_{\mu}\Phi(x,\mu)(y)|^{2})\mu(dy)<\infty. \end{align*} $$
If
![]() $\Phi \in \mathcal {C}(\mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
and
$\Phi \in \mathcal {C}(\mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
and
![]() $\Phi \geq 0$
, then we say that
$\Phi \geq 0$
, then we say that
![]() $\Phi \in \mathcal {C}_{+}(\mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
.
$\Phi \in \mathcal {C}_{+}(\mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d}))$
.
For (1.1), we make the following assumptions.
Assumption 2.7. Functions
![]() $b,\sigma $
are continuous with respect to
$b,\sigma $
are continuous with respect to
![]() $(x,\mu )\kern1.4pt{\in}\kern1.4pt \mathbb {R}^{d}\kern1.4pt{\times}\kern1.4pt \mathcal {M}_{\lambda ^{2}}(\mathbb {R}^{d})$
, and there is a constant
$(x,\mu )\kern1.4pt{\in}\kern1.4pt \mathbb {R}^{d}\kern1.4pt{\times}\kern1.4pt \mathcal {M}_{\lambda ^{2}}(\mathbb {R}^{d})$
, and there is a constant
![]() $L_1>0$
such that
$L_1>0$
such that
Assumption 2.8. There is a constant
![]() $L_2>0$
such that
$L_2>0$
such that
Assumption 2.9. There exists a function
![]() $v(\cdot ,\cdot ): \mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})\to \mathbb {R}$
such that:
$v(\cdot ,\cdot ): \mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{p}}(\mathbb {R}^{d})\to \mathbb {R}$
such that:
-
(i)
 $v\in \mathcal {C}_{+}(\mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{2}}(\mathbb {R}^{d}))$
;
$v\in \mathcal {C}_{+}(\mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{2}}(\mathbb {R}^{d}))$
; -
(ii)
 $\int _{\mathbb {R}^{d}}(L^{\mu }v(x,\mu )+\gamma v(x,\mu ))\mu (dx)\leq 0$
;
$\int _{\mathbb {R}^{d}}(L^{\mu }v(x,\mu )+\gamma v(x,\mu ))\mu (dx)\leq 0$
; -
(iii) for some
 $p\geq 1$
,
$p\geq 1$
,
 $a_{1}\int _{\mathbb {R}^{d}}|x|^{p}\mu (dx)\leq \int _{\mathbb {R}^{d}}v(x,\mu )\mu (dx)\leq a_{2}\int _{\mathbb {R}^{d}}|x|^{p}\mu (dx)$
.
$a_{1}\int _{\mathbb {R}^{d}}|x|^{p}\mu (dx)\leq \int _{\mathbb {R}^{d}}v(x,\mu )\mu (dx)\leq a_{2}\int _{\mathbb {R}^{d}}|x|^{p}\mu (dx)$
.
By the classical result of Wang [Reference Wang19], under Assumptions 2.7–2.9, there exists a unique strong solution
![]() $X_t^{x_0}$
, with initial value
$X_t^{x_0}$
, with initial value
![]() $x_0$
, to (1.1), and for
$x_0$
, to (1.1), and for
![]() $p\geq 2$
,
$p\geq 2$
,
![]() $\mathbb {E}\sup _{0\leq t\leq T}|X^{x_0}_{t}|^{p}<\infty $
. Let
$\mathbb {E}\sup _{0\leq t\leq T}|X^{x_0}_{t}|^{p}<\infty $
. Let
![]() $C^{2}(\mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{2}}(\mathbb {R}^{d});\mathbb {R}^{+})$
denote the space of nonnegative functions which are continuous and twice differentiable. For
$C^{2}(\mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{2}}(\mathbb {R}^{d});\mathbb {R}^{+})$
denote the space of nonnegative functions which are continuous and twice differentiable. For
![]() $V\in C^{2}(\mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{2}}(\mathbb {R}^{d});\mathbb {R}^{+})$
, we have the following generator of (1.1):
$V\in C^{2}(\mathbb {R}^{d}\times \mathcal {M}_{\lambda ^{2}}(\mathbb {R}^{d});\mathbb {R}^{+})$
, we have the following generator of (1.1):
 $$ \begin{align*} L^{\mu}V(x,\mu)&=(b^{i}\partial_{x_{i}})(x,\mu)+\frac{1}{2}((\sigma\sigma^{*})^{ij}\partial^{2}_{x_{i}x_{j}})(x,\mu)+\int_{\mathbb{R}^{d}}b^{i}(y,\mu)(\partial_{\mu}V)_{i}(x,\mu)(y)\mu(dy)\nonumber\\&\quad+\frac{1}{2}\int_{\mathbb{R}^{d}}(\sigma\sigma^{*})^{ij}(y,\mu)\partial_{y_{i}}(\partial_{\mu}V)_{j}(y)\mu(dy)\,. \end{align*} $$
$$ \begin{align*} L^{\mu}V(x,\mu)&=(b^{i}\partial_{x_{i}})(x,\mu)+\frac{1}{2}((\sigma\sigma^{*})^{ij}\partial^{2}_{x_{i}x_{j}})(x,\mu)+\int_{\mathbb{R}^{d}}b^{i}(y,\mu)(\partial_{\mu}V)_{i}(x,\mu)(y)\mu(dy)\nonumber\\&\quad+\frac{1}{2}\int_{\mathbb{R}^{d}}(\sigma\sigma^{*})^{ij}(y,\mu)\partial_{y_{i}}(\partial_{\mu}V)_{j}(y)\mu(dy)\,. \end{align*} $$
Remark 2.10. In fact, the strong solution to (1.1) defines a Markov process [Reference Wang19]. Let
![]() $p(t,x_{0},dz)$
be the transition probability distribution to process
$p(t,x_{0},dz)$
be the transition probability distribution to process
![]() $X_{t}^{x_{0}}$
and
$X_{t}^{x_{0}}$
and
![]() $p(t,x_{0},\Gamma )$
be the probability for the event
$p(t,x_{0},\Gamma )$
be the probability for the event
![]() $\{X^{x_0}_{t}\in \Gamma \}$
with the initial value
$\{X^{x_0}_{t}\in \Gamma \}$
with the initial value
![]() $x_{0}$
, that is,
$x_{0}$
, that is,
Definition 2.11. The process
![]() $X_{t}^{x_{0}}$
with initial value
$X_{t}^{x_{0}}$
with initial value
![]() $x_{0}$
is called stable in distribution if there exists a probability measure
$x_{0}$
is called stable in distribution if there exists a probability measure
![]() $\Pi (\cdot )$
such that for any initial value
$\Pi (\cdot )$
such that for any initial value
![]() $x_{0}$
, its transition probability
$x_{0}$
, its transition probability
![]() $p(t,x_{0},dz)$
weakly converges to
$p(t,x_{0},dz)$
weakly converges to
![]() $\Pi (\cdot )$
, as
$\Pi (\cdot )$
, as
![]() $t\to \infty $
. Equation (1.1) is said to be stable in distribution if
$t\to \infty $
. Equation (1.1) is said to be stable in distribution if
![]() $X_{t}^{x_{0}}$
is stable in distribution.
$X_{t}^{x_{0}}$
is stable in distribution.
To study the stability in distribution, we need the following assumption. First, for a given function
![]() $U\in C^{2}(\mathbb {R}^{d}; \mathbb {R})$
, we define the operator
$U\in C^{2}(\mathbb {R}^{d}; \mathbb {R})$
, we define the operator
 $$ \begin{align*} L(x,y,\mu,\nu)U(x-y)&=[b(x,\mu)-b(y,\nu)]U_{x}(x-y)\nonumber\\ &\quad +\tfrac{1}{2}Tr[(\sigma(x,\mu)-\sigma(y,\nu))^{*}U_{xx}(x-y)(\sigma(x,\mu)-\sigma(y,\nu))]. \end{align*} $$
$$ \begin{align*} L(x,y,\mu,\nu)U(x-y)&=[b(x,\mu)-b(y,\nu)]U_{x}(x-y)\nonumber\\ &\quad +\tfrac{1}{2}Tr[(\sigma(x,\mu)-\sigma(y,\nu))^{*}U_{xx}(x-y)(\sigma(x,\mu)-\sigma(y,\nu))]. \end{align*} $$
Assumption 2.12. There exist a function
![]() $U\in C^{2}(\mathbb {R}^{d};\mathbb {R}_{+})$
and a constant
$U\in C^{2}(\mathbb {R}^{d};\mathbb {R}_{+})$
and a constant
![]() $K>0$
, such that for any two solutions
$K>0$
, such that for any two solutions
![]() $(X_{t}^{x_{0}})_{t\geq 0}$
and
$(X_{t}^{x_{0}})_{t\geq 0}$
and
![]() $(X_{t}^{y_{0}})_{t\geq 0}$
with its distributions
$(X_{t}^{y_{0}})_{t\geq 0}$
with its distributions
![]() $\mathcal {L}(X_{t}^{x_{0}})=\mu _{t}$
and
$\mathcal {L}(X_{t}^{x_{0}})=\mu _{t}$
and
![]() $\mathcal {L}(X_{t}^{y_{0}})=\nu _{t}$
, and for all couplings
$\mathcal {L}(X_{t}^{y_{0}})=\nu _{t}$
, and for all couplings
![]() $\pi \in \Pi (\mu _{t},\nu _{t})$
,
$\pi \in \Pi (\mu _{t},\nu _{t})$
,
3. Stability analysis
3.1. Exponential stability
This section gives the exponential stability in the pth moment and in a.s. sense.
Definition 3.1. Let
![]() $p\geq 1$
. The solution
$p\geq 1$
. The solution
![]() $X_{t}^{x_{0}}$
of (1.1) is said to be pth moment exponentially stable if there is a pair of constants
$X_{t}^{x_{0}}$
of (1.1) is said to be pth moment exponentially stable if there is a pair of constants
![]() $\gamma>0$
and
$\gamma>0$
and
![]() $C>0$
such that
$C>0$
such that
Further, it is said to be a.s. exponentially stable if
 $$ \begin{align*} \limsup_{t\to\infty}\frac{\mathrm{\log}|X_{t}^{x_{0}}|}{t}\leq -\gamma,\quad \text{a.s}. \end{align*} $$
$$ \begin{align*} \limsup_{t\to\infty}\frac{\mathrm{\log}|X_{t}^{x_{0}}|}{t}\leq -\gamma,\quad \text{a.s}. \end{align*} $$
For this, we further assume that for some constant
![]() $N>0$
and
$N>0$
and
![]() $p\geq 1$
,
$p\geq 1$
,
Theorem 3.2. Assume that Assumptions
2.7–2.9
hold. For every
![]() $x_{0}\in \mathbb {R}^{d}$
,
$x_{0}\in \mathbb {R}^{d}$
,
![]() $X_{t}^{x_{0}}$
is pth moment exponentially stable and a.s. exponentially stable. Furthermore, for every
$X_{t}^{x_{0}}$
is pth moment exponentially stable and a.s. exponentially stable. Furthermore, for every
![]() ${\epsilon>0}$
, there exists an
${\epsilon>0}$
, there exists an
![]() $R>0$
such that for all
$R>0$
such that for all
![]() $t\geq 0$
,
$t\geq 0$
,
![]() $\mathbb {P}\{|X_{t}^{x_{0}}|\geq R\}<\epsilon $
.
$\mathbb {P}\{|X_{t}^{x_{0}}|\geq R\}<\epsilon $
.
Proof. For
![]() $x_{0}\in \mathbb {R}^{d}$
, let
$x_{0}\in \mathbb {R}^{d}$
, let
![]() $X_{t}^{x_{0}}$
be the solution of (1.1), for positive integer k, define the stopping times
$X_{t}^{x_{0}}$
be the solution of (1.1), for positive integer k, define the stopping times
then obviously,
![]() $\rho _{k}\to \infty $
, a.s. as
$\rho _{k}\to \infty $
, a.s. as
![]() $k\to \infty $
. Then for the stopped processes
$k\to \infty $
. Then for the stopped processes
![]() $(X_{t\wedge \rho _{k}}^{x_{0}})_{t\geq 0}$
, function v and distribution processes
$(X_{t\wedge \rho _{k}}^{x_{0}})_{t\geq 0}$
, function v and distribution processes
![]() $\mathcal {L}(X_{t}^{x_{0}})_{t\geq 0}$
, by It
$\mathcal {L}(X_{t}^{x_{0}})_{t\geq 0}$
, by It
![]() $\mathrm {\hat {o}}$
’s formula [Reference Hammersley, Siska and Szpruch9],
$\mathrm {\hat {o}}$
’s formula [Reference Hammersley, Siska and Szpruch9],
 $$ \begin{align*} e^{\gamma(t\wedge\rho_{k})}v(X_{t\wedge\rho_{k}}^{x_{0}},\ &\mathcal{L}(X_{t}^{x_{0}}))-v(x_{0},\delta_{x_{0}}) \\ &=\int_{0}^{t}\gamma e^{\gamma(s\wedge\rho_{k})}v(X_{s\wedge\rho_{k}}^{x_{0}},\mathcal{L}(X_{s}^{x_{0}}))\,ds \\ &\quad +\int_{0}^{t}e^{\gamma(s\wedge\rho_{k})}(b^{i}\partial_{x_{i}}v)(X_{s\wedge\rho_{k}}^{x_{0}},\mathcal{L}(X_{s}^{x_{0}}))\,ds\nonumber\\ &\quad+\frac{1}{2}\int_{0}^{t}e^{\gamma(s\wedge\rho_{k})}((\sigma\sigma^{*})^{ij}\partial_{x_{i}x_{j}}^{2}v)(X_{s\wedge\rho_{k}}^{x_{0}},\mathcal{L}(X_{s}^{x_{0}}))\,ds\nonumber\\ &\quad+\int_{0}^{t}e^{\gamma(s\wedge\rho_{k})}(\partial_{x_{i}}v\sigma^{ij})(X_{s\wedge\rho_{k}}^{x_{0}},\mathcal{L}(X_{s}^{x_{0}}))\,dW_{s}^{j}\nonumber\\ &\quad+\int_{0}^{t}\int_{\mathbb{R}^{d}}e^{\gamma(s\wedge\rho_{k})}((b^{i}\partial_{x_{i}}v)(X_{s\wedge\rho_{k}}^{x_{0}},\mathcal{L}(X_{s}^{x_{0}}))(y)\mathcal{L}(X_{s}^{x_{0}})(dy)\,ds\nonumber\\ &\quad+\frac{1}{2}\int_{0}^{t}\int_{\mathbb{R}^{d}}e^{\gamma(s\wedge\rho_{k})}(\sigma\sigma^{*})^{ij}(X_{s\wedge\rho_{k}}^{x_{0}},\mathcal{L}(X_{s}^{x_{0}}))(y)\mathcal{L}(X_{s}^{x_{0}})(dy)\,ds. \end{align*} $$
$$ \begin{align*} e^{\gamma(t\wedge\rho_{k})}v(X_{t\wedge\rho_{k}}^{x_{0}},\ &\mathcal{L}(X_{t}^{x_{0}}))-v(x_{0},\delta_{x_{0}}) \\ &=\int_{0}^{t}\gamma e^{\gamma(s\wedge\rho_{k})}v(X_{s\wedge\rho_{k}}^{x_{0}},\mathcal{L}(X_{s}^{x_{0}}))\,ds \\ &\quad +\int_{0}^{t}e^{\gamma(s\wedge\rho_{k})}(b^{i}\partial_{x_{i}}v)(X_{s\wedge\rho_{k}}^{x_{0}},\mathcal{L}(X_{s}^{x_{0}}))\,ds\nonumber\\ &\quad+\frac{1}{2}\int_{0}^{t}e^{\gamma(s\wedge\rho_{k})}((\sigma\sigma^{*})^{ij}\partial_{x_{i}x_{j}}^{2}v)(X_{s\wedge\rho_{k}}^{x_{0}},\mathcal{L}(X_{s}^{x_{0}}))\,ds\nonumber\\ &\quad+\int_{0}^{t}e^{\gamma(s\wedge\rho_{k})}(\partial_{x_{i}}v\sigma^{ij})(X_{s\wedge\rho_{k}}^{x_{0}},\mathcal{L}(X_{s}^{x_{0}}))\,dW_{s}^{j}\nonumber\\ &\quad+\int_{0}^{t}\int_{\mathbb{R}^{d}}e^{\gamma(s\wedge\rho_{k})}((b^{i}\partial_{x_{i}}v)(X_{s\wedge\rho_{k}}^{x_{0}},\mathcal{L}(X_{s}^{x_{0}}))(y)\mathcal{L}(X_{s}^{x_{0}})(dy)\,ds\nonumber\\ &\quad+\frac{1}{2}\int_{0}^{t}\int_{\mathbb{R}^{d}}e^{\gamma(s\wedge\rho_{k})}(\sigma\sigma^{*})^{ij}(X_{s\wedge\rho_{k}}^{x_{0}},\mathcal{L}(X_{s}^{x_{0}}))(y)\mathcal{L}(X_{s}^{x_{0}})(dy)\,ds. \end{align*} $$
Then taking expectation, by Assumption 2.9,
Let
![]() $k\to \infty $
and together with the Fatou lemma [Reference Ethier and Kurtz7],
$k\to \infty $
and together with the Fatou lemma [Reference Ethier and Kurtz7],
Furthermore, by Assumption 2.7,
Thus,
Then by Chebyshev’s inequality [Reference Ethier and Kurtz7], for
![]() $R>0$
,
$R>0$
,
Noticing that from (1.1),
 $$ \begin{align*} X_{t+s}^{x_{0}}=X_{t}^{x_{0}}+\int_{t}^{t+s}b(X_{u}^{x_{0}},\mathcal{L}(X_{u}^{x_{0}}))\,du+\int_{t}^{t+s}\sigma(X_{u}^{x_{0}},\mathcal{L}(X_{u}^{x_{0}}))\,dW_{u}, \end{align*} $$
$$ \begin{align*} X_{t+s}^{x_{0}}=X_{t}^{x_{0}}+\int_{t}^{t+s}b(X_{u}^{x_{0}},\mathcal{L}(X_{u}^{x_{0}}))\,du+\int_{t}^{t+s}\sigma(X_{u}^{x_{0}},\mathcal{L}(X_{u}^{x_{0}}))\,dW_{u}, \end{align*} $$
and for
![]() $p\geq 1$
,
$p\geq 1$
,
![]() $\tau>0$
, by (3.1),
$\tau>0$
, by (3.1),
 $$ \begin{align*} \mathbb{E}\sup_{0\leq s\leq \tau}|X_{t+s}^{x_{0}}|^{p}&\leq C_{p}\mathbb{E}|X_{t}^{x_{0}}|^{p}+C_{p}\mathbb{E}\sup_{0\leq s\leq \tau}\Big|\int_{t}^{t+s}b(X_{u}^{x_{0}},\mathcal{L}(X_{u}^{x_{0}}))\,du\Big|^{p}\nonumber\\&\quad +C_{p}\mathbb{E}\sup_{0\leq s\leq \tau}\Big|\int_{t}^{t+s}\sigma(X_{u}^{x_{0}},\mathcal{L}(X_{u}^{x_{0}}))\,dW_{u}\Big|^{p}\nonumber\\&\leq C_{p}\mathbb{E}|X_{t}^{x_{0}}|^{p}+C_{p,\tau}\mathbb{E}\int_{t}^{t+\tau}|b(X_{u}^{x_{0}},\mathcal{L}(X_{u}^{x_{0}}))|^{p}\,du \\&\quad +C_{p}\mathbb{E}\int_{t}^{t+\tau}|\sigma(X_{u}^{x_{0}},\mathcal{L}(X_{u}^{x_{0}}))|^{p}\,du\nonumber\\&\leq C_{p}\mathbb{E}|X_{t}^{x_{0}}|^{p} +C_{p,\tau,N}\mathbb{E}\int_{t}^{t+\tau}\bigg(|X_{u}^{x_{0}}|^{p}+\int_{\mathbb{R}^{d}}|x|^{p}\mathcal{L}(X_{u}^{x_{0}})(dx)\bigg)\,du\nonumber\\&\leq C_{p}\mathbb{E}|X_{t}^{x_{0}}|^{p}+C_{p,\tau,N}\int_{t}^{t+\tau}\mathbb{E}|X_{u}^{x_{0}}|^{p}\,du\nonumber\\&\leq C_{p,x_{0}}e^{-\gamma t}+C_{p,\tau,x_{0},N}\int_{t}^{t+\tau}e^{-\gamma u}\,du\leq C_{p,\tau,x_{0},\gamma,N}e^{-\gamma t}. \end{align*} $$
$$ \begin{align*} \mathbb{E}\sup_{0\leq s\leq \tau}|X_{t+s}^{x_{0}}|^{p}&\leq C_{p}\mathbb{E}|X_{t}^{x_{0}}|^{p}+C_{p}\mathbb{E}\sup_{0\leq s\leq \tau}\Big|\int_{t}^{t+s}b(X_{u}^{x_{0}},\mathcal{L}(X_{u}^{x_{0}}))\,du\Big|^{p}\nonumber\\&\quad +C_{p}\mathbb{E}\sup_{0\leq s\leq \tau}\Big|\int_{t}^{t+s}\sigma(X_{u}^{x_{0}},\mathcal{L}(X_{u}^{x_{0}}))\,dW_{u}\Big|^{p}\nonumber\\&\leq C_{p}\mathbb{E}|X_{t}^{x_{0}}|^{p}+C_{p,\tau}\mathbb{E}\int_{t}^{t+\tau}|b(X_{u}^{x_{0}},\mathcal{L}(X_{u}^{x_{0}}))|^{p}\,du \\&\quad +C_{p}\mathbb{E}\int_{t}^{t+\tau}|\sigma(X_{u}^{x_{0}},\mathcal{L}(X_{u}^{x_{0}}))|^{p}\,du\nonumber\\&\leq C_{p}\mathbb{E}|X_{t}^{x_{0}}|^{p} +C_{p,\tau,N}\mathbb{E}\int_{t}^{t+\tau}\bigg(|X_{u}^{x_{0}}|^{p}+\int_{\mathbb{R}^{d}}|x|^{p}\mathcal{L}(X_{u}^{x_{0}})(dx)\bigg)\,du\nonumber\\&\leq C_{p}\mathbb{E}|X_{t}^{x_{0}}|^{p}+C_{p,\tau,N}\int_{t}^{t+\tau}\mathbb{E}|X_{u}^{x_{0}}|^{p}\,du\nonumber\\&\leq C_{p,x_{0}}e^{-\gamma t}+C_{p,\tau,x_{0},N}\int_{t}^{t+\tau}e^{-\gamma u}\,du\leq C_{p,\tau,x_{0},\gamma,N}e^{-\gamma t}. \end{align*} $$
Then for
![]() $n=1,2, \dots $
,
$n=1,2, \dots $
,
thus, for
![]() $\epsilon \in (0,\gamma )$
and
$\epsilon \in (0,\gamma )$
and
![]() $n\in \mathbb {N}$
, by Chebychev’s inequality,
$n\in \mathbb {N}$
, by Chebychev’s inequality,
 $$ \begin{align*} \mathbb{P}\bigg(\omega: \sup_{n\tau\leq t\leq (n+1)\tau}|X_{t}^{x_{0}}|^{p}>e^{-(\gamma-\epsilon)n\tau}\bigg)\leq C_{p,\tau,x_{0},\gamma,N}e^{-\epsilon n\tau}. \end{align*} $$
$$ \begin{align*} \mathbb{P}\bigg(\omega: \sup_{n\tau\leq t\leq (n+1)\tau}|X_{t}^{x_{0}}|^{p}>e^{-(\gamma-\epsilon)n\tau}\bigg)\leq C_{p,\tau,x_{0},\gamma,N}e^{-\epsilon n\tau}. \end{align*} $$
By the Borel–Cantelli lemma [Reference Kallenberg11], there exists a random constant
![]() $n_{0}(\omega )$
such that for almost all
$n_{0}(\omega )$
such that for almost all
![]() $\omega \in \Omega $
, for
$\omega \in \Omega $
, for
![]() $n>n_{0}(\omega )$
,
$n>n_{0}(\omega )$
,
Thus, for any
![]() $n\tau \leq t\leq (n+1)\tau $
,
$n\tau \leq t\leq (n+1)\tau $
,
 $$ \begin{align*} \frac{\mathrm{\log}|X_{t}^{x_{0}}|}{t}=\frac{\mathrm{\log}|X_{t}^{x_{0}}|^{p}}{pt}\leq \frac{\mathrm{\log}\sup_{n\tau\leq t\leq (n+1)\tau}|X_{t}^{x_{0}}|^{p}}{pn\tau}\leq -\frac{\gamma-\epsilon}{p},\quad\text{a.s.}, \end{align*} $$
$$ \begin{align*} \frac{\mathrm{\log}|X_{t}^{x_{0}}|}{t}=\frac{\mathrm{\log}|X_{t}^{x_{0}}|^{p}}{pt}\leq \frac{\mathrm{\log}\sup_{n\tau\leq t\leq (n+1)\tau}|X_{t}^{x_{0}}|^{p}}{pn\tau}\leq -\frac{\gamma-\epsilon}{p},\quad\text{a.s.}, \end{align*} $$
and
 $$ \begin{align*} \limsup_{t\to\infty}\frac{\mathrm{\log}|X_{t}^{x_{0}}|}{t}\leq -\frac{\gamma-\epsilon}{p},\quad \text{a.s.} \end{align*} $$
$$ \begin{align*} \limsup_{t\to\infty}\frac{\mathrm{\log}|X_{t}^{x_{0}}|}{t}\leq -\frac{\gamma-\epsilon}{p},\quad \text{a.s.} \end{align*} $$
Now letting
![]() $\epsilon \to 0$
, the proof is complete.
$\epsilon \to 0$
, the proof is complete.
Remark 3.3. From Theorem 3.2, the transition probability family
![]() $\{p(t,x_{0},dz)\mid t\geq 0\}$
is tight, that is, for
$\{p(t,x_{0},dz)\mid t\geq 0\}$
is tight, that is, for
![]() $\epsilon>0$
, there exists a compact set
$\epsilon>0$
, there exists a compact set
![]() $\mathcal {K}=\mathcal {K}(x_{0},\epsilon )$
such that
$\mathcal {K}=\mathcal {K}(x_{0},\epsilon )$
such that
3.2. Stability in distribution
Next, we consider the stability in distribution. For this, we need to consider the difference between two solutions with different initial values, that is,
 $$ \begin{align*} X_{t}^{x_{0}}-X_{t}^{y_{0}}&=x_{0}-y_{0}+\int_{0}^{t}[b(X_{s}^{x_{0}},\mathcal{L}(X_{s}^{x_{0}}))-b(X_{s}^{y_{0}},\mathcal{L}(X_{s}^{y_{0}}))]\,ds\nonumber\\ &\quad +\int_{0}^{t}[\sigma(X_{s}^{x_{0}},\mathcal{L}(X_{s}^{x_{0}}))-\sigma(X_{s}^{y_{0}},\mathcal{L}(X_{s}^{y_{0}}))]\,dW_{s}. \end{align*} $$
$$ \begin{align*} X_{t}^{x_{0}}-X_{t}^{y_{0}}&=x_{0}-y_{0}+\int_{0}^{t}[b(X_{s}^{x_{0}},\mathcal{L}(X_{s}^{x_{0}}))-b(X_{s}^{y_{0}},\mathcal{L}(X_{s}^{y_{0}}))]\,ds\nonumber\\ &\quad +\int_{0}^{t}[\sigma(X_{s}^{x_{0}},\mathcal{L}(X_{s}^{x_{0}}))-\sigma(X_{s}^{y_{0}},\mathcal{L}(X_{s}^{y_{0}}))]\,dW_{s}. \end{align*} $$
We need two more notation. Let
![]() $\mathcal {H}$
be the set consisting of nondecreasing functions
$\mathcal {H}$
be the set consisting of nondecreasing functions
![]() $K: \mathbb {R}_{+}\to \mathbb {R}_{+}$
such that
$K: \mathbb {R}_{+}\to \mathbb {R}_{+}$
such that
![]() $K(0)=0$
, and
$K(0)=0$
, and
![]() $\mathcal {H}_{\infty }$
be the set of functions
$\mathcal {H}_{\infty }$
be the set of functions
![]() $K\in \mathcal {H}$
such that
$K\in \mathcal {H}$
such that
![]() $K(x)\to \infty $
as
$K(x)\to \infty $
as
![]() $x\to \infty $
.
$x\to \infty $
.
Lemma 3.4. If there exists a function
![]() $U\in C^{2}(\mathbb {R}^{d};\mathbb {R}_{+})$
satisfying
$U\in C^{2}(\mathbb {R}^{d};\mathbb {R}_{+})$
satisfying
![]() $U(0)=0$
and a function
$U(0)=0$
and a function
![]() $\alpha _{1}\in \mathcal {H}_{\infty }$
such that
$\alpha _{1}\in \mathcal {H}_{\infty }$
such that
then for every
![]() $\epsilon>0$
and compact set
$\epsilon>0$
and compact set
![]() $\mathcal {K}$
on
$\mathcal {K}$
on
![]() $\mathbb {R}^{d}$
, there exists
$\mathbb {R}^{d}$
, there exists
![]() $T=T(\mathcal {K},\epsilon )>0$
such that
$T=T(\mathcal {K},\epsilon )>0$
such that
For the convenience of presentation in the following, we rewrite (1.1) as
 $$ \begin{align} X_{t}^{x_{0}}=x_{0}+\int_{0}^{t}\tilde{b}(u,X_{u}^{x_{0}})\, du+\int_{0}^{t}\tilde{\sigma}(u,X_{u}^{x_{0}})\,dW_{u}, \quad t\geq0, \end{align} $$
$$ \begin{align} X_{t}^{x_{0}}=x_{0}+\int_{0}^{t}\tilde{b}(u,X_{u}^{x_{0}})\, du+\int_{0}^{t}\tilde{\sigma}(u,X_{u}^{x_{0}})\,dW_{u}, \quad t\geq0, \end{align} $$
where
![]() $\tilde {b}(u,X_{u}^{x_{0}})=b(X_{u}^{x_{0}},\mathcal {L}(X_{u}^{x_{0}}))$
and
$\tilde {b}(u,X_{u}^{x_{0}})=b(X_{u}^{x_{0}},\mathcal {L}(X_{u}^{x_{0}}))$
and
![]() $\tilde {\sigma }(u,X_{u}^{x_{0}})=\sigma (X_{u}^{x_{0}},\mathcal {L}(X_{u}^{x_{0}}))$
. Since (1.1) has a unique strong solution
$\tilde {\sigma }(u,X_{u}^{x_{0}})=\sigma (X_{u}^{x_{0}},\mathcal {L}(X_{u}^{x_{0}}))$
. Since (1.1) has a unique strong solution
![]() $(X_{t}^{x_{0}})_{t\geq 0}$
with the initial distribution
$(X_{t}^{x_{0}})_{t\geq 0}$
with the initial distribution
![]() $\delta _{x_{0}}$
, the distribution of process
$\delta _{x_{0}}$
, the distribution of process
![]() $(X_{t}^{x_{0}})_{t\geq 0}$
is known, and (3.2) is a classic SDE. Then, the solution of (3.2) is a strong Markov process [Reference Ding and Qiao5, Lemma 5.3].
$(X_{t}^{x_{0}})_{t\geq 0}$
is known, and (3.2) is a classic SDE. Then, the solution of (3.2) is a strong Markov process [Reference Ding and Qiao5, Lemma 5.3].
Proof of Lemma 3.4.
For
![]() $\epsilon>0$
, by the continuity of function U with
$\epsilon>0$
, by the continuity of function U with
![]() $U(0)=0$
, we choose
$U(0)=0$
, we choose
![]() $\alpha \in (0,\epsilon )$
small enough such that
$\alpha \in (0,\epsilon )$
small enough such that
 $$ \begin{align*} \frac{\sup_{|x|\leq \alpha}U(x)}{\mu_{1}(\epsilon)}<\frac{\epsilon}{2}. \end{align*} $$
$$ \begin{align*} \frac{\sup_{|x|\leq \alpha}U(x)}{\mu_{1}(\epsilon)}<\frac{\epsilon}{2}. \end{align*} $$
Let
![]() $\mathcal {K}$
be a compact set on
$\mathcal {K}$
be a compact set on
![]() $\mathbb {R}^{d}$
and for fixed
$\mathbb {R}^{d}$
and for fixed
![]() $x_{0}$
,
$x_{0}$
,
![]() $y_{0}\in \mathcal {K}$
and
$y_{0}\in \mathcal {K}$
and
![]() $\beta>\alpha $
, we define two stopping times
$\beta>\alpha $
, we define two stopping times
 $$ \begin{align*} \tau_{\alpha}&=\inf\{t\geq0\mid |X_{t}^{x_{0}}-X_{t}^{y_{0}}|\leq \alpha\}, \\[.1cm] \tau_{\beta}&=\inf\{t\geq0\mid |X_{t}^{x_{0}}-X_{t}^{y_{0}}|\geq \beta\}. \end{align*} $$
$$ \begin{align*} \tau_{\alpha}&=\inf\{t\geq0\mid |X_{t}^{x_{0}}-X_{t}^{y_{0}}|\leq \alpha\}, \\[.1cm] \tau_{\beta}&=\inf\{t\geq0\mid |X_{t}^{x_{0}}-X_{t}^{y_{0}}|\geq \beta\}. \end{align*} $$
By It
![]() $\mathrm {\hat {o}}$
’s formula for the stopped process
$\mathrm {\hat {o}}$
’s formula for the stopped process
![]() $U(X_{\tau _{\beta }\wedge t}^{x_{0}}-X_{\tau _{\beta }\wedge t}^{y_{0}})$
and Assumption 2.12,
$U(X_{\tau _{\beta }\wedge t}^{x_{0}}-X_{\tau _{\beta }\wedge t}^{y_{0}})$
and Assumption 2.12,
 $$ \begin{align*} \mathbb{E}U(X_{\tau_{\beta}\wedge t}^{x_{0}}-X_{\tau_{\beta}\wedge t}^{y_{0}})&\leq U(x_{0}-y_{0})-K\int_{0}^{\tau_{\beta}\wedge t}U(X_{s}^{x_{0}}-X_{s}^{y_{0}})\,ds\nonumber\\ &\quad +\mathbb{E}\int_{0}^{\tau_{\beta}\wedge t}U_{x}(X_{s}^{x_{0}}-X_{s}^{y_{0}})(\tilde{\sigma}(s,X_{s}^{x_{0}})-\tilde{\sigma}(u,X_{s}^{y_{0}}))\,dW_{s}\nonumber\\ &=U(x_{0}-y_{0})-K\int_{0}^{\tau_{\beta}\wedge t}U(X_{s}^{x_{0}}-X_{s}^{y_{0}})\,ds. \end{align*} $$
$$ \begin{align*} \mathbb{E}U(X_{\tau_{\beta}\wedge t}^{x_{0}}-X_{\tau_{\beta}\wedge t}^{y_{0}})&\leq U(x_{0}-y_{0})-K\int_{0}^{\tau_{\beta}\wedge t}U(X_{s}^{x_{0}}-X_{s}^{y_{0}})\,ds\nonumber\\ &\quad +\mathbb{E}\int_{0}^{\tau_{\beta}\wedge t}U_{x}(X_{s}^{x_{0}}-X_{s}^{y_{0}})(\tilde{\sigma}(s,X_{s}^{x_{0}})-\tilde{\sigma}(u,X_{s}^{y_{0}}))\,dW_{s}\nonumber\\ &=U(x_{0}-y_{0})-K\int_{0}^{\tau_{\beta}\wedge t}U(X_{s}^{x_{0}}-X_{s}^{y_{0}})\,ds. \end{align*} $$
Then,
that is,
Notice that for all
![]() $x_{0}, y_{0}\in \mathcal {K}$
and
$x_{0}, y_{0}\in \mathcal {K}$
and
![]() $U(x_{0}-y_{0})$
bounded, there exists
$U(x_{0}-y_{0})$
bounded, there exists
![]() $\beta =\beta (\mathcal {K},\epsilon )>0$
such that
$\beta =\beta (\mathcal {K},\epsilon )>0$
such that
Fix the
![]() $\beta $
and let
$\beta $
and let
![]() $t_{\alpha }=\tau _{\alpha }\wedge \tau _{\beta }\wedge t$
, then similar discussion yields
$t_{\alpha }=\tau _{\alpha }\wedge \tau _{\beta }\wedge t$
, then similar discussion yields
 $$ \begin{align*} \mathbb{E}U(X_{t_{\alpha}}^{x_{0}}-X_{t_{\alpha}}^{y_{0}})&\leq U(x_{0}-y_{0})-K\mathbb{E}\int_{0}^{t_{\alpha}}U(X_{s}^{x_{0}}-X_{s}^{y_{0}})\,ds\nonumber\\ &\leq U(x_{0}-y_{0})-K\mathbb{E}\int_{0}^{t_{\alpha}}\alpha_{1}(|X_{s}^{x_{0}}-X_{s}^{y_{0}}|)\,ds\nonumber\\ &\leq U(x_{0}-y_{0})-K\alpha_{1}(\alpha)\mathbb{E}(\tau_{\alpha}\wedge\tau_{\beta}\wedge t), \end{align*} $$
$$ \begin{align*} \mathbb{E}U(X_{t_{\alpha}}^{x_{0}}-X_{t_{\alpha}}^{y_{0}})&\leq U(x_{0}-y_{0})-K\mathbb{E}\int_{0}^{t_{\alpha}}U(X_{s}^{x_{0}}-X_{s}^{y_{0}})\,ds\nonumber\\ &\leq U(x_{0}-y_{0})-K\mathbb{E}\int_{0}^{t_{\alpha}}\alpha_{1}(|X_{s}^{x_{0}}-X_{s}^{y_{0}}|)\,ds\nonumber\\ &\leq U(x_{0}-y_{0})-K\alpha_{1}(\alpha)\mathbb{E}(\tau_{\alpha}\wedge\tau_{\beta}\wedge t), \end{align*} $$
which implies that
Moreover, this implies that for a given
![]() $\epsilon \in (0,1)$
, there exists
$\epsilon \in (0,1)$
, there exists
![]() $T=T(\mathcal {K},\epsilon )>0$
such that
$T=T(\mathcal {K},\epsilon )>0$
such that
Thus,
 $$ \begin{align*} 1-\frac{\epsilon}{4}<\mathbb{P}\{\tau_{\alpha}\wedge\tau_{\beta}\leq T\}&\leq \mathbb{P}\{\tau_{\alpha}\leq T\}+\mathbb{P}(\tau_{\beta}\leq T)\nonumber\\ &\leq \mathbb{P}\{\tau_{\alpha}\leq T\}+\mathbb{P}(\tau_{\beta}\leq\infty)\nonumber\\ &\leq \mathbb{P}\{\tau_{\alpha}\leq T\}+\frac{\epsilon}{4} \end{align*} $$
$$ \begin{align*} 1-\frac{\epsilon}{4}<\mathbb{P}\{\tau_{\alpha}\wedge\tau_{\beta}\leq T\}&\leq \mathbb{P}\{\tau_{\alpha}\leq T\}+\mathbb{P}(\tau_{\beta}\leq T)\nonumber\\ &\leq \mathbb{P}\{\tau_{\alpha}\leq T\}+\mathbb{P}(\tau_{\beta}\leq\infty)\nonumber\\ &\leq \mathbb{P}\{\tau_{\alpha}\leq T\}+\frac{\epsilon}{4} \end{align*} $$
and
Now we define the stopping time
Let
![]() $t>T$
, then
$t>T$
, then
 $$ \begin{align*} \mathbb{P}({\tau_{\alpha}\leq T}\cap{\sigma\leq t})\mu_{1}(\epsilon)&\leq\mathbb{E}(I_{\tau_{\alpha}\leq T,\sigma\leq t}U(X_{t\wedge\sigma}^{x_{0}}-X_{t\wedge\sigma}^{y_{0}}))\nonumber\\ &\leq\mathbb{E}(I_{\tau_{\alpha}\leq T}U(X_{t\wedge\tau_{\alpha}}^{x_{0}}-X_{t\wedge\tau_{\alpha}}^{y_{0}}))\nonumber\\ &\leq\mathbb{E}(I_{\tau_{\alpha}\leq T}U(X_{\tau_{\alpha}}^{x_{0}}-X_{\tau_{\alpha}}^{y_{0}}))\leq\mathbb{P}({\tau_{\alpha}\leq T})\sup_{|x|\leq\alpha}U(x). \end{align*} $$
$$ \begin{align*} \mathbb{P}({\tau_{\alpha}\leq T}\cap{\sigma\leq t})\mu_{1}(\epsilon)&\leq\mathbb{E}(I_{\tau_{\alpha}\leq T,\sigma\leq t}U(X_{t\wedge\sigma}^{x_{0}}-X_{t\wedge\sigma}^{y_{0}}))\nonumber\\ &\leq\mathbb{E}(I_{\tau_{\alpha}\leq T}U(X_{t\wedge\tau_{\alpha}}^{x_{0}}-X_{t\wedge\tau_{\alpha}}^{y_{0}}))\nonumber\\ &\leq\mathbb{E}(I_{\tau_{\alpha}\leq T}U(X_{\tau_{\alpha}}^{x_{0}}-X_{\tau_{\alpha}}^{y_{0}}))\leq\mathbb{P}({\tau_{\alpha}\leq T})\sup_{|x|\leq\alpha}U(x). \end{align*} $$
Thus,
and
Let
![]() $t\to \infty $
, then
$t\to \infty $
, then
This indicates that for all
![]() $x_{0}$
,
$x_{0}$
,
![]() $y_{0}\in \mathcal {K}$
,
$y_{0}\in \mathcal {K}$
,
![]() $t\geq T$
,
$t\geq T$
,
This completes the proof.
Lemma 3.5. For every compact set
![]() $\mathcal {K}$
,
$\mathcal {K}$
,
Proof. We only need to show that there exists
![]() $T>0$
, such that for all
$T>0$
, such that for all
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $x_{0}$
,
$x_{0}$
,
![]() $y_{0}\in \mathcal {K}$
,
$y_{0}\in \mathcal {K}$
,
It is equivalent to show that
However, notice that for every
![]() $\phi \in C_{\lambda }(\mathbb {R}^{d})$
,
$\phi \in C_{\lambda }(\mathbb {R}^{d})$
,
By Lemma 3.4, there exists a
![]() $T_{1}>0$
such that
$T_{1}>0$
such that
Due to the arbitrariness of
![]() $\phi \in C_{\lambda }(\mathbb {R}^{d})$
,
$\phi \in C_{\lambda }(\mathbb {R}^{d})$
,
The proof is now complete.
Lemma 3.6. Under the assumptions of Theorem
3.2
and Lemma
3.4
, for
![]() $x_0\in \mathbb {R}^d$
,
$x_0\in \mathbb {R}^d$
,
![]() $\{p(t,x_{0},\cdot )\,, t\geq 0\}$
is a Cauchy sequence.
$\{p(t,x_{0},\cdot )\,, t\geq 0\}$
is a Cauchy sequence.
Proof. We need to show that for every
![]() $x_{0}\in \mathbb {R}^{d}$
and
$x_{0}\in \mathbb {R}^{d}$
and
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $T>0$
such that for
$T>0$
such that for
![]() $t\geq T$
and
$t\geq T$
and
![]() $s>0$
,
$s>0$
,
which is equivalent that for every
![]() $\phi \in C_{\lambda }(\mathbb {R}^{d})$
,
$\phi \in C_{\lambda }(\mathbb {R}^{d})$
,
By Lemma 3.2, there exists a compact set
![]() $\mathcal {K}$
on
$\mathcal {K}$
on
![]() $\mathbb {R}^{d}$
such that for
$\mathbb {R}^{d}$
such that for
![]() $\epsilon>0$
,
$\epsilon>0$
,
Furthermore, by the strong Markov property of
![]() $X_{t}^{x_{0}}$
, for
$X_{t}^{x_{0}}$
, for
![]() $\phi \in C_{\lambda }(\mathbb {R}^{d})$
and t,
$\phi \in C_{\lambda }(\mathbb {R}^{d})$
and t,
![]() $s>0$
,
$s>0$
,
 $$ \begin{align*} |\mathbb{E}\phi(X_{t+s}^{x_{0}})-\mathbb{E}\phi(X_{t}^{x_{0}})|&=|\mathbb{E}[\mathbb{E}(\phi(X_{t+s}^{x_{0}})|\mathcal{F}_{s})]-\mathbb{E}\phi(X_{t}^{x_{0}})|\nonumber\\ &=|\mathbb{E}[\mathbb{E}\phi(X_{t}^{s,X_{s}^{x_{0}}})]-\mathbb{E}\phi(X_{t}^{x_{0}})|\nonumber\\ &=\Big|\!\int_{\mathbb{R}^{d}}\mathbb{E}\phi(X_{t}^{z})p(s,x_{0},dz)-\mathbb{E}\phi(X_{t}^{x_{0}})\Big|\nonumber\\ &\leq\int_{\mathbb{R}^{d}}\mathbb{E}|\phi(X_{t}^{z})-\phi(X_{t}^{x_{0}})|p(s,x_{0},dz)\nonumber\\ &=\int_{\mathcal{K}}\mathbb{E}|\phi(X_{t}^{z})-\phi(X_{t}^{x_{0}})|p(s,x_{0},dz)\nonumber\\ &\quad+\int_{\mathbb{R}^{d}-\mathcal{K}}\mathbb{E}|\phi(X_{t}^{z})-\phi(X_{t}^{x_{0}})|p(s,x_{0},dz)\nonumber\\ &\leq\int_{\mathcal{K}}\mathbb{E}|\phi(X_{t}^{z})-\phi(X_{t}^{x_{0}})|p(s,x_{0},dz)+\frac{\epsilon}{4}. \end{align*} $$
$$ \begin{align*} |\mathbb{E}\phi(X_{t+s}^{x_{0}})-\mathbb{E}\phi(X_{t}^{x_{0}})|&=|\mathbb{E}[\mathbb{E}(\phi(X_{t+s}^{x_{0}})|\mathcal{F}_{s})]-\mathbb{E}\phi(X_{t}^{x_{0}})|\nonumber\\ &=|\mathbb{E}[\mathbb{E}\phi(X_{t}^{s,X_{s}^{x_{0}}})]-\mathbb{E}\phi(X_{t}^{x_{0}})|\nonumber\\ &=\Big|\!\int_{\mathbb{R}^{d}}\mathbb{E}\phi(X_{t}^{z})p(s,x_{0},dz)-\mathbb{E}\phi(X_{t}^{x_{0}})\Big|\nonumber\\ &\leq\int_{\mathbb{R}^{d}}\mathbb{E}|\phi(X_{t}^{z})-\phi(X_{t}^{x_{0}})|p(s,x_{0},dz)\nonumber\\ &=\int_{\mathcal{K}}\mathbb{E}|\phi(X_{t}^{z})-\phi(X_{t}^{x_{0}})|p(s,x_{0},dz)\nonumber\\ &\quad+\int_{\mathbb{R}^{d}-\mathcal{K}}\mathbb{E}|\phi(X_{t}^{z})-\phi(X_{t}^{x_{0}})|p(s,x_{0},dz)\nonumber\\ &\leq\int_{\mathcal{K}}\mathbb{E}|\phi(X_{t}^{z})-\phi(X_{t}^{x_{0}})|p(s,x_{0},dz)+\frac{\epsilon}{4}. \end{align*} $$
By Lemma 3.4, there exists
![]() $T>0$
such that for every
$T>0$
such that for every
![]() $\epsilon>0$
,
$\epsilon>0$
,
Thus,
which completes the proof.
Proof. By Definition 2.11, we need to show that there exists a probability measure
![]() $\pi (\cdot )$
such that for every
$\pi (\cdot )$
such that for every
![]() $x_{0}\in \mathbb {R}^{d}$
, the transition probability family
$x_{0}\in \mathbb {R}^{d}$
, the transition probability family
![]() $\{p(t,x_{0},\cdot ): t\geq 0\}$
weakly converges to
$\{p(t,x_{0},\cdot ): t\geq 0\}$
weakly converges to
![]() $\pi (\cdot )$
. In fact, we show that for every
$\pi (\cdot )$
. In fact, we show that for every
![]() $x\in \mathbb {R}^{d}$
,
$x\in \mathbb {R}^{d}$
,
By Lemma 3.6,
![]() $\{p(t,0,\cdot ): t\geq 0\}$
is a Cauchy sequence in
$\{p(t,0,\cdot ): t\geq 0\}$
is a Cauchy sequence in
![]() $\mathcal {P}(\mathbb {R}^{d})$
with the metric
$\mathcal {P}(\mathbb {R}^{d})$
with the metric
![]() $\rho $
. Since
$\rho $
. Since
![]() $\mathcal {P}(\mathbb {R}^{d})$
is a complete metric space, there exists a probability measure
$\mathcal {P}(\mathbb {R}^{d})$
is a complete metric space, there exists a probability measure
![]() $\pi (\cdot )\in \mathcal {P}(\mathbb {R}^{d})$
such that
$\pi (\cdot )\in \mathcal {P}(\mathbb {R}^{d})$
such that
By a triangle inequality,
 $$ \begin{align*} \lim_{t\to\infty}\rho(p(t,x,\cdot),\pi(\cdot))&\leq \lim_{t\to\infty}\rho(p(t,x,\cdot),p(t,0,\cdot))+\lim_{t\to\infty}\rho(p(t,0,\cdot),\pi(\cdot)) \\ &=0. \end{align*} $$
$$ \begin{align*} \lim_{t\to\infty}\rho(p(t,x,\cdot),\pi(\cdot))&\leq \lim_{t\to\infty}\rho(p(t,x,\cdot),p(t,0,\cdot))+\lim_{t\to\infty}\rho(p(t,0,\cdot),\pi(\cdot)) \\ &=0. \end{align*} $$
The proof is complete.
4. Conclusions
In the study, we first prove the pth moment exponential stability and a.s. exponential stability of the solution of (1.1) by using the distribution-dependent It
![]() $\mathrm {\hat {o}}$
's formula, and then obtain the tightness of the transition probability family corresponding to the solution of (1.1). Based on this, we introduce a distribution-dependent operator, that is, Assumption 2.12, and combined with the method of Yuan and Mao [Reference Yuan and Mao21], we get that when the time is long enough, the transition probability family tends to a unique probability measure, that is, the solution of (1.1) is asymptotically stable in distribution. It would be valuable to use a similar method to analyse the long time behaviour of (1.1) with jump noise.
$\mathrm {\hat {o}}$
's formula, and then obtain the tightness of the transition probability family corresponding to the solution of (1.1). Based on this, we introduce a distribution-dependent operator, that is, Assumption 2.12, and combined with the method of Yuan and Mao [Reference Yuan and Mao21], we get that when the time is long enough, the transition probability family tends to a unique probability measure, that is, the solution of (1.1) is asymptotically stable in distribution. It would be valuable to use a similar method to analyse the long time behaviour of (1.1) with jump noise.
Acknowledgements
This research is supported by the Natural Science Foundation of Jiangsu Province (BK20230899) and the National Natural Science Foundation of China (11771207).