19 results
On approximation of the analytic fixed finite time large t probability distributions in an extreme renewal process with no-mean inter-renewals
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 20 May 2022, pp. 695-710
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scattering by PEC half-plane and disk placed on parallel planes
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 15 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 19 April 2022, pp. 311-321
-
- Article
- Export citation
2 - Mathematical Preliminaries
-
- Book:
- Introduction to the Finite Element Method and Implementation with MATLAB®
- Published online:
- 09 December 2020
- Print publication:
- 30 July 2020, pp 16-51
-
- Chapter
- Export citation
INTEGRAL EQUATION FORMULATION FOR SHOUT OPTIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 60 / Issue 1 / July 2018
- Published online by Cambridge University Press:
- 08 August 2018, pp. 65-85
-
- Article
-
- You have access
- Export citation
Explicit flock solutions for Quasi-Morse potentials
-
- Journal:
- European Journal of Applied Mathematics / Volume 25 / Issue 5 / October 2014
- Published online by Cambridge University Press:
- 15 April 2014, pp. 553-578
-
- Article
-
- You have access
- Open access
- Export citation
Electromagnetic scattering at composite objects : a novelmulti-trace boundary integral formulation
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 46 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 31 May 2012, pp. 1421-1445
- Print publication:
- November 2012
-
- Article
- Export citation
INTEGRAL EQUATION METHODS IN CHANGE-POINT DETECTION PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 28 February 2012, pp. 518-520
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Exponential convergence of hp quadraturefor integral operators with Gevrey kernels
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 45 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 11 October 2010, pp. 387-422
- Print publication:
- May 2011
-
- Article
- Export citation
On constant-sign periodic solutions in modelling the spread of interdependent epidemics
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 3 / January 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 309-332
-
- Article
-
- You have access
- Export citation
THE SET OF SOLUTIONS OF INTEGRODIFFERENTIAL EQUATIONS IN BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 507-522
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Approximation by generalized impedance boundary conditions of atransmission problem in acoustic scattering
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 5 / September 2005
- Published online by Cambridge University Press:
- 15 September 2005, pp. 1041-1059
- Print publication:
- September 2005
-
- Article
- Export citation
SYSTEMS OF INTEGRAL EQUATIONS WITH WEIGHTED DIFFERENCE KERNELS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 47 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 27 May 2004, pp. 205-230
-
- Article
-
- You have access
- Export citation
On the time-dependent occupancy and backlog distributions for the GI/G/∞ queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 558-569
- Print publication:
- June 1999
-
- Article
- Export citation
On the Compound Generalized Poisson Distributions
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 24 / Issue 2 / November 1994
- Published online by Cambridge University Press:
- 29 August 2014, pp. 255-263
- Print publication:
- November 1994
-
- Article
-
- You have access
- Export citation
Boundaries with negative jumps for the Brownian motion
-
- Journal:
- Journal of Applied Probability / Volume 22 / Issue 4 / December 1985
- Published online by Cambridge University Press:
- 14 July 2016, pp. 964-970
- Print publication:
- December 1985
-
- Article
- Export citation
Analysis of two parallel queues by common exit service and infinite queue size
-
- Journal:
- Advances in Applied Probability / Volume 13 / Issue 1 / March 1981
- Published online by Cambridge University Press:
- 01 July 2016, pp. 147-166
- Print publication:
- March 1981
-
- Article
- Export citation
Sequential random packing in the plane
-
- Journal:
- Journal of Applied Probability / Volume 15 / Issue 4 / December 1978
- Published online by Cambridge University Press:
- 14 July 2016, pp. 803-814
- Print publication:
- December 1978
-
- Article
- Export citation
Conditional moments in a critical age-dependent branching process
-
- Journal:
- Journal of Applied Probability / Volume 12 / Issue 3 / September 1975
- Published online by Cambridge University Press:
- 14 July 2016, pp. 581-587
- Print publication:
- September 1975
-
- Article
- Export citation
On the limiting behaviour of a basic stochastic process
-
- Journal:
- Journal of Applied Probability / Volume 9 / Issue 1 / March 1972
- Published online by Cambridge University Press:
- 14 July 2016, pp. 202-207
- Print publication:
- March 1972
-
- Article
- Export citation

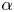
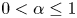
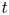
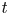
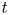
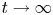
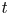
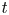




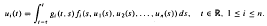
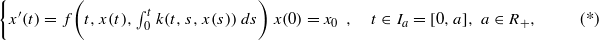
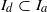 .
.
