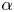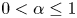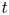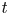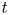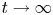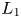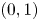1. Introduction
The analytic fixed finite time ![]() $t\gt0$ probability density functions (pdfs) of excess, age, and total life in a renewal process, are of interest theoretically, and to applied probabilists, engineers, and scientists (see Figure 1 in Section 2.1). Feller [Reference Feller8], Smith [Reference Smith20], Cox [Reference Cox7], Karlin and Taylor [Reference Karlin and Taylor11], Ross [Reference Ross15] pp. 44–45, and others have usually considered these pdfs when the inter-renewals are continuous variates with a finite mean. Recent work in applied probability and stochastic modeling has generated interest in the analytic fixed finite time
$t\gt0$ probability density functions (pdfs) of excess, age, and total life in a renewal process, are of interest theoretically, and to applied probabilists, engineers, and scientists (see Figure 1 in Section 2.1). Feller [Reference Feller8], Smith [Reference Smith20], Cox [Reference Cox7], Karlin and Taylor [Reference Karlin and Taylor11], Ross [Reference Ross15] pp. 44–45, and others have usually considered these pdfs when the inter-renewals are continuous variates with a finite mean. Recent work in applied probability and stochastic modeling has generated interest in the analytic fixed finite time ![]() $t$ pdfs of excess, age, and total life in a renewal processes where the inter-renewals are no-mean, heavy-tailed Pareto(II) variates [Reference Arnold2] p. 49 and [Reference Kleiber and Kotz12]. Real-world applications of the Pareto(II) distribution are given in, for example, Huang et al. [Reference Huang, Coia and Brill10] and Harris et al. [Reference Harris, Brill and Fischer9]. (Note: The Pareto(II) distribution is also called the Lomax distribution [Reference Lomax13].)
$t$ pdfs of excess, age, and total life in a renewal processes where the inter-renewals are no-mean, heavy-tailed Pareto(II) variates [Reference Arnold2] p. 49 and [Reference Kleiber and Kotz12]. Real-world applications of the Pareto(II) distribution are given in, for example, Huang et al. [Reference Huang, Coia and Brill10] and Harris et al. [Reference Harris, Brill and Fischer9]. (Note: The Pareto(II) distribution is also called the Lomax distribution [Reference Lomax13].)

Figure 1. One-dimensional illustration showing the fixed finite time ![]() $t$ excess, age, and total life—
$t$ excess, age, and total life—![]() $Z_{N(t)+1}$ (
$Z_{N(t)+1}$ (![]() $=$ age
$=$ age ![]() $+$ excess). Figure shows
$+$ excess). Figure shows ![]() $Z_{N(t)+1}$ relative to the fixed finite time
$Z_{N(t)+1}$ relative to the fixed finite time ![]() $t$ in the extreme renewal process
$t$ in the extreme renewal process ![]() $\{ {Z}_{ {n}}\}_{{n=1,2,\ldots }}$.
$\{ {Z}_{ {n}}\}_{{n=1,2,\ldots }}$.
Here, the extreme renewal process of interest has no-mean Pareto(II) inter-renewals with a shape parameter ![]() $\alpha \in (0,1]$, (formula (3.5), p. 60 in [Reference Kleiber and Kotz12]; formula (1.3.5), p. 11 with
$\alpha \in (0,1]$, (formula (3.5), p. 60 in [Reference Kleiber and Kotz12]; formula (1.3.5), p. 11 with ![]() $\mu =0$ and
$\mu =0$ and ![]() $\sigma =1$ in [Reference Arnold2]). We propose a method to approximate the analytic fixed finite time
$\sigma =1$ in [Reference Arnold2]). We propose a method to approximate the analytic fixed finite time ![]() $t$ pdfs of excess, age, and total life for large
$t$ pdfs of excess, age, and total life for large ![]() $t$ in this extreme renewal process. In that process, the analytic fixed finite time
$t$ in this extreme renewal process. In that process, the analytic fixed finite time ![]() $t$ pdfs exist (
$t$ pdfs exist (![]() $0\lt t\lt\infty$), but the corresponding limiting pdfs as
$0\lt t\lt\infty$), but the corresponding limiting pdfs as ![]() $t\rightarrow \infty$ do not exist because the inter-renewals have no mean (Section 2.2).
$t\rightarrow \infty$ do not exist because the inter-renewals have no mean (Section 2.2).
Generally, two steps involving extensive computations are required to derive integral expressions for the analytic pdfs of the fixed finite time ![]() $t$ excess, age, and total life. Step 1 creates and solves a Volterra integral equation of the second kind for the limiting pdf of a basic underlying regenerative process, denoted by
$t$ excess, age, and total life. Step 1 creates and solves a Volterra integral equation of the second kind for the limiting pdf of a basic underlying regenerative process, denoted by ![]() $\{ X_{{\rm RG}}(s)\}_{s\geq 0}$ (subscript
$\{ X_{{\rm RG}}(s)\}_{s\geq 0}$ (subscript ![]() ${\rm RG}$ indicates “regenerative process”). Process
${\rm RG}$ indicates “regenerative process”). Process ![]() $\{ X_{{\rm RG}}(s)\}_{s\geq 0}$ is used to derive integral expressions for all three fixed finite time
$\{ X_{{\rm RG}}(s)\}_{s\geq 0}$ is used to derive integral expressions for all three fixed finite time ![]() $t$ pdfs (see Figure 3 in Section 3). It has a threshold at the state-space fixed finite level
$t$ pdfs (see Figure 3 in Section 3). It has a threshold at the state-space fixed finite level ![]() $t$ of interest. Process
$t$ of interest. Process ![]() $\{ X_{{\rm RG}}(s)\}_{s\geq 0}$ is built of an infinite sequence of i.i.d. (independent and identically distributed) realizations of the extreme renewal process
$\{ X_{{\rm RG}}(s)\}_{s\geq 0}$ is built of an infinite sequence of i.i.d. (independent and identically distributed) realizations of the extreme renewal process ![]() $\{Z_{n}\}_{n=1,2,\ldots }$. In
$\{Z_{n}\}_{n=1,2,\ldots }$. In ![]() $\{ X_{{\rm RG}}(s)\}_{s\geq 0}$, the stationary mixed pdf as
$\{ X_{{\rm RG}}(s)\}_{s\geq 0}$, the stationary mixed pdf as ![]() $s\rightarrow \infty$ exists (e.g., [Reference Sigman and Wolff18,Reference Smith20]). We denote this mixed pdf by
$s\rightarrow \infty$ exists (e.g., [Reference Sigman and Wolff18,Reference Smith20]). We denote this mixed pdf by ![]() $\{ \pi _{{\rm RG},0}^{(t)},f_{{\rm RG}}^{(t)}(x)\}_{x\in (0,t)}$, where
$\{ \pi _{{\rm RG},0}^{(t)},f_{{\rm RG}}^{(t)}(x)\}_{x\in (0,t)}$, where ![]() $\pi _{{\rm RG},0}^{(t)} = \lim _{s\rightarrow \infty } P(X_{{\rm RG}}(s)=0)$; it is derived using a stochastic LC method (Section 3). Step 2 derives integral expressions for all three analytic fixed finite time
$\pi _{{\rm RG},0}^{(t)} = \lim _{s\rightarrow \infty } P(X_{{\rm RG}}(s)=0)$; it is derived using a stochastic LC method (Section 3). Step 2 derives integral expressions for all three analytic fixed finite time ![]() $t$ pdfs in
$t$ pdfs in ![]() $\{Z_{n}\}_{n=1,2,\ldots }$, in terms of
$\{Z_{n}\}_{n=1,2,\ldots }$, in terms of ![]() $\{ \pi _{{\rm RG},0}^{(t)},f_{{\rm RG}}^{(t)}(x)\}_{0\lt x\lt t}$ (Section 3.2).
$\{ \pi _{{\rm RG},0}^{(t)},f_{{\rm RG}}^{(t)}(x)\}_{0\lt x\lt t}$ (Section 3.2).
Our goal is to approximate the analytic fixed finite time large ![]() $t$ pdfs by applying the corresponding limiting pdfs of a companion renewal process where the inter-renewals are right-truncated Pareto(II) variates. These limiting pdfs have well-known formulas, so their derivations require no computations (see Section 2.5).
$t$ pdfs by applying the corresponding limiting pdfs of a companion renewal process where the inter-renewals are right-truncated Pareto(II) variates. These limiting pdfs have well-known formulas, so their derivations require no computations (see Section 2.5).
We approximate the analytic fixed finite time ![]() $t$ pdfs of excess, age, and total life in
$t$ pdfs of excess, age, and total life in ![]() $\{Z_{n}\}_{n=1,2,\ldots }$ for large
$\{Z_{n}\}_{n=1,2,\ldots }$ for large ![]() $t$ using the corresponding limiting pdfs in the companion renewal process
$t$ using the corresponding limiting pdfs in the companion renewal process ![]() $\{Z_{K\!,n}^{{\rm TR}}\}_{{n=1,2,\ldots }}$ having right-truncated inter-renewals. The right truncation point
$\{Z_{K\!,n}^{{\rm TR}}\}_{{n=1,2,\ldots }}$ having right-truncated inter-renewals. The right truncation point ![]() $K$ of
$K$ of ![]() $Z_{K}^{{\rm TR}}$ is selected to satisfy a “plausible criterion” for the approximation to be “close” over a nontrivial subset of
$Z_{K}^{{\rm TR}}$ is selected to satisfy a “plausible criterion” for the approximation to be “close” over a nontrivial subset of ![]() $( 0,K)$ (Section 4).
$( 0,K)$ (Section 4).
Section 5.1 gives a measure of distance between the analytic fixed finite time ![]() $t$ pdfs in
$t$ pdfs in ![]() $\{Z_{n}\}_{n=1,2,\ldots }$ and the approximating limiting pdfs in
$\{Z_{n}\}_{n=1,2,\ldots }$ and the approximating limiting pdfs in ![]() $\{Z_{K\!,n}^{{\rm TR}}\}_{{n=1,2,\ldots }}$, using an
$\{Z_{K\!,n}^{{\rm TR}}\}_{{n=1,2,\ldots }}$, using an ![]() $L_{1}$ metric taking values in
$L_{1}$ metric taking values in ![]() $(0,1)$. We choose a measure equal to one-half of the area between the two pdfs, because it conveniently takes values in
$(0,1)$. We choose a measure equal to one-half of the area between the two pdfs, because it conveniently takes values in ![]() $(0,1)$. A distance measure “near
$(0,1)$. A distance measure “near ![]() $0$” indicates that the approximation is “close”. A distance measure “near
$0$” indicates that the approximation is “close”. A distance measure “near ![]() $1$” indicates that the approximation is “far”.
$1$” indicates that the approximation is “far”.
Section 2 on preliminaries gives notation and properties about the standard Pareto(II) variable, which are used later in the paper; and for the renewal process whose inter-renewals are Pareto(II) variates. It also gives similar details about the right-truncated Pareto(II) distribution. Section 2.1 defines the fixed finite time-![]() $t$ random variables. Section 2.2 further details the extreme renewal process. Section 2.3 describes the right-truncated Pareto(II) random variables. Section 2.4 gives the expected value of the truncated Pareto(II) random variable, required for the limiting pdfs of the excess, age, and total life variables. Section 2.5 further details the renewal process with right-truncated Pareto(II) inter-renewals, giving the very simple formulas for the limiting pdfs of excess, age, and total life. Section 3 details the underlying regenerative process
$t$ random variables. Section 2.2 further details the extreme renewal process. Section 2.3 describes the right-truncated Pareto(II) random variables. Section 2.4 gives the expected value of the truncated Pareto(II) random variable, required for the limiting pdfs of the excess, age, and total life variables. Section 2.5 further details the renewal process with right-truncated Pareto(II) inter-renewals, giving the very simple formulas for the limiting pdfs of excess, age, and total life. Section 3 details the underlying regenerative process ![]() $\{ X_{{\rm RG}}(s)\}_{s\geq 0}$. Section 4 approximates the analytic fixed finite time
$\{ X_{{\rm RG}}(s)\}_{s\geq 0}$. Section 4 approximates the analytic fixed finite time ![]() $t$ pdfs (large
$t$ pdfs (large ![]() $t$) of the extreme renewal process. Section 5 gives an
$t$) of the extreme renewal process. Section 5 gives an ![]() $L_{1}$ measure of distance between the analytic fixed finite time
$L_{1}$ measure of distance between the analytic fixed finite time ![]() $t$ pdfs for large
$t$ pdfs for large ![]() $t$ in the extreme renewal process, and in the corresponding approximating limiting pdfs in the renewal process with right-truncated Pareto(II) inter-renewals.
$t$ in the extreme renewal process, and in the corresponding approximating limiting pdfs in the renewal process with right-truncated Pareto(II) inter-renewals.
2. Preliminaries
This section presents preliminary results which are useful in the sequel. It describes the positions of the three fixed finite time ![]() $t$ random variables of interest in the extreme renewal process
$t$ random variables of interest in the extreme renewal process ![]() $\{ Z_{n}\}_{n=1,2,\ldots }$ (Figure 1); specifies the probability distributions of Pareto(II)
$\{ Z_{n}\}_{n=1,2,\ldots }$ (Figure 1); specifies the probability distributions of Pareto(II)![]() $(x,\alpha )$, and right-truncated Pareto(II)
$(x,\alpha )$, and right-truncated Pareto(II)![]() $(x,\alpha )$ when the truncation point is
$(x,\alpha )$ when the truncation point is ![]() $K\gt0$; details the limiting pdfs of excess, age, and total life in the renewal process with right-truncated inter-renewals (denoted by
$K\gt0$; details the limiting pdfs of excess, age, and total life in the renewal process with right-truncated inter-renewals (denoted by ![]() $\{Z_{K\!,n}^{{\rm TR}}\}_{{n=1,2,\ldots }}$).
$\{Z_{K\!,n}^{{\rm TR}}\}_{{n=1,2,\ldots }}$).
2.1. The three fixed finite time  $t$ pdfs in the extreme renewal process
$t$ pdfs in the extreme renewal process
Figure 1 shows a sketch of an extreme renewal process where the inter-renewal times are i.i.d. Pareto(II) r.v.s (random variables) ![]() $\{ Z_{n}\}_{n=1,2,\ldots }$, showing the variates of interest: excess, age, and total life with respect to fixed finite time
$\{ Z_{n}\}_{n=1,2,\ldots }$, showing the variates of interest: excess, age, and total life with respect to fixed finite time ![]() $t$.
$t$.
2.2. The Pareto(II) probability distribution for inter-renewals of the extreme renewal process  ${\{Z_{n}\}_{n=1,2,\ldots }}$
${\{Z_{n}\}_{n=1,2,\ldots }}$
Consider the Pareto(II) inter-renewals of the extreme renewal process. Denote the cdf, ccdf (complementary cdf), and pdf of each inter-renewal in ![]() $\{Z_{n}\}_{n=1,2,\ldots }$ by:
$\{Z_{n}\}_{n=1,2,\ldots }$ by: ![]() $B(x)$;
$B(x)$; ![]() $\bar {B}(x) := 1-B(x)$,
$\bar {B}(x) := 1-B(x)$, ![]() $0\leq x\lt\infty$; and
$0\leq x\lt\infty$; and ![]() $b(x)$,
$b(x)$, ![]() $0\lt x\lt\infty,$ respectively. The inter-renewals
$0\lt x\lt\infty,$ respectively. The inter-renewals ![]() $Z_{ {n}} \overset {d}{=} Z \overset {d}{=} {\rm Pareto(II)}(x,\alpha ),\ 0\leq x\lt\infty,$
$Z_{ {n}} \overset {d}{=} Z \overset {d}{=} {\rm Pareto(II)}(x,\alpha ),\ 0\leq x\lt\infty,$ ![]() $\alpha \in (0,1]$, where
$\alpha \in (0,1]$, where
 \begin{equation} \left.\begin{array}{l} B(x) = 1-( 1+x)^{-\alpha },\quad 0\leq x\lt\infty, \\ \bar{B}(x) =1-B(x)=( 1+x)^{-\alpha },\quad 0\leq x\lt\infty, \\ b(x)=\dfrac{d}{dx}B(x)=\alpha ( {1+x})^{-{\alpha -1} },\quad 0\lt x\lt\infty, \end{array}\right\} \end{equation}
\begin{equation} \left.\begin{array}{l} B(x) = 1-( 1+x)^{-\alpha },\quad 0\leq x\lt\infty, \\ \bar{B}(x) =1-B(x)=( 1+x)^{-\alpha },\quad 0\leq x\lt\infty, \\ b(x)=\dfrac{d}{dx}B(x)=\alpha ( {1+x})^{-{\alpha -1} },\quad 0\lt x\lt\infty, \end{array}\right\} \end{equation}where ![]() $B(x)\equiv P(Z\leq x)$. Then,
$B(x)\equiv P(Z\leq x)$. Then, ![]() $Z$ is heavy-tailed [Reference Sigman17]. Since
$Z$ is heavy-tailed [Reference Sigman17]. Since ![]() $\alpha \in (0,1]$,
$\alpha \in (0,1]$, ![]() $Z$ has no mean, implying that the limiting pdfs of excess, age, and total life do not exist.
$Z$ has no mean, implying that the limiting pdfs of excess, age, and total life do not exist.
We will use the shape parameter ![]() $\alpha =0.5$ throughout for illustrative purposes. For any value of
$\alpha =0.5$ throughout for illustrative purposes. For any value of ![]() $\alpha \in (0,1]$, the analysis would be similar.
$\alpha \in (0,1]$, the analysis would be similar.
Consider the 1-dimensional illustration of the extreme renewal process ![]() $\{Z_{n}\}_{n=1,2,\ldots }$ in Figure 1. The fixed finite time point of interest is
$\{Z_{n}\}_{n=1,2,\ldots }$ in Figure 1. The fixed finite time point of interest is ![]() $t\gt0$. Also,
$t\gt0$. Also, ![]() $N(t)$ := number of renewals in the interval
$N(t)$ := number of renewals in the interval ![]() $(0,t)$. Let
$(0,t)$. Let ![]() $N_{t}$ := number of renewals required to first exceed
$N_{t}$ := number of renewals required to first exceed ![]() $t$, that is,
$t$, that is, ![]() $N_{t} := \min \{n|\sum _{{i=1}}^{{n}}Z_{{i}} \gt t\}$. Then,
$N_{t} := \min \{n|\sum _{{i=1}}^{{n}}Z_{{i}} \gt t\}$. Then, ![]() $N_{t}$ is a stopping time for
$N_{t}$ is a stopping time for ![]() $\{Z_{n}\}_{n=1,2,\ldots }$. Also,
$\{Z_{n}\}_{n=1,2,\ldots }$. Also, ![]() $N_{t}= N(t)+1$, and
$N_{t}= N(t)+1$, and ![]() $E[ N_{t}] = E[ N(t)] +1 \equiv M(t)+1$, where
$E[ N_{t}] = E[ N(t)] +1 \equiv M(t)+1$, where ![]() $M(t)\equiv E[ N(t)]$ is the “renewal function” (see, e.g., [Reference Karlin and Taylor11] pp. 167–169).
$M(t)\equiv E[ N(t)]$ is the “renewal function” (see, e.g., [Reference Karlin and Taylor11] pp. 167–169).
In ![]() $\{Z_{n}\}_{n=1,2,\ldots }$, the fixed finite time
$\{Z_{n}\}_{n=1,2,\ldots }$, the fixed finite time ![]() $t$ pdfs of excess, age, and total life exist [Reference Brill4]. But the corresponding limiting pdfs of excess, age, and total life as
$t$ pdfs of excess, age, and total life exist [Reference Brill4]. But the corresponding limiting pdfs of excess, age, and total life as ![]() $t\rightarrow \infty$, do not exist because
$t\rightarrow \infty$, do not exist because ![]() $Z_{n}$ has no mean.
$Z_{n}$ has no mean.
2.3. The truncated Pareto(II) probability distribution in the companion renewal process
Define a companion renewal process ![]() $\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$ related to, but distinct from
$\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$ related to, but distinct from ![]() $\{ Z_{n}\}_{n=1,2,\ldots }$, where the inter-renewals are:
$\{ Z_{n}\}_{n=1,2,\ldots }$, where the inter-renewals are: ![]() $Z_{K\!,n}^{\textrm {TR}}\overset {d}{=}Z_{K}^{\textrm {TR}}\overset {d}{=} \textrm {right-truncated Pareto(II)}(x,\alpha ),\ 0\lt x\lt K$. The superscript “
$Z_{K\!,n}^{\textrm {TR}}\overset {d}{=}Z_{K}^{\textrm {TR}}\overset {d}{=} \textrm {right-truncated Pareto(II)}(x,\alpha ),\ 0\lt x\lt K$. The superscript “![]() $\textrm {TR}$” indicates that
$\textrm {TR}$” indicates that ![]() $K := \textrm {right truncation point of}\ Z$. In
$K := \textrm {right truncation point of}\ Z$. In ![]() $\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$, the limiting pdfs of excess, age, and total life, as
$\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$, the limiting pdfs of excess, age, and total life, as ![]() $t\rightarrow \infty$, do exist because
$t\rightarrow \infty$, do exist because ![]() $E[ Z_{K}^{\textrm {TR}}]\lt\infty$ (finite). Importantly, the limiting pdfs of excess, age, and total life in
$E[ Z_{K}^{\textrm {TR}}]\lt\infty$ (finite). Importantly, the limiting pdfs of excess, age, and total life in ![]() $\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$ have relatively simple formulas (Section 2.5).
$\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$ have relatively simple formulas (Section 2.5).
We use the limiting pdfs of excess, age, and total life in ![]() $\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$ to approximate the analytic fixed finite time
$\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$ to approximate the analytic fixed finite time ![]() $t$ pdfs of interest (large
$t$ pdfs of interest (large ![]() $t$) in the extreme renewal process
$t$) in the extreme renewal process ![]() $\{ Z_{n}\}_{n=1,2,\ldots }$. No computations are required since the theoretical formulas of the limiting pdfs are well known. This approximation method saves a great deal of computer time required for the computational derivation of the analytic fixed finite time
$\{ Z_{n}\}_{n=1,2,\ldots }$. No computations are required since the theoretical formulas of the limiting pdfs are well known. This approximation method saves a great deal of computer time required for the computational derivation of the analytic fixed finite time ![]() $t$ pdfs, for even a single large
$t$ pdfs, for even a single large ![]() $t$.
$t$.
Substituting from formula (1) in Section 2.2, we obtain the truncated cdf ![]() $B_{K}^{\textrm {TR}}(x)$, ccdf
$B_{K}^{\textrm {TR}}(x)$, ccdf ![]() $\overline {B_{K}^{\textrm {TR}}}(x)$, and pdf
$\overline {B_{K}^{\textrm {TR}}}(x)$, and pdf ![]() $b_{K}^{\textrm {TR}}(x)$, of
$b_{K}^{\textrm {TR}}(x)$, of ![]() $Z_{K}^{\textrm {TR}}$ to be, respectively:
$Z_{K}^{\textrm {TR}}$ to be, respectively:
 \begin{equation} \left.\begin{array}{l} B_{K}^{{\rm TR}}(x)=\dfrac{B(x)}{B(K)}=\dfrac{1-( 1+x)^{-\alpha }}{ 1-( 1+K)^{-\alpha }},\quad 0\lt x\lt K, \\ \overline{B_{K}^{{\rm TR}}}(x) =1-B_{K}^{{\rm TR}}(x)=1-\dfrac{1-( 1+x)^{-\alpha }}{1-( 1+K)^{-\alpha }},\quad 0\lt x\lt K, \\ b_{K}^{{\rm TR}}(x)=\dfrac{d}{dx}B_{K}^{{\rm TR}}(x)=\dfrac{\alpha ( {1+x})^{-{\alpha -1}}}{1-( 1+K)^{-\alpha }},\quad 0\lt x\lt K\text{.} \end{array}\right\} \end{equation}
\begin{equation} \left.\begin{array}{l} B_{K}^{{\rm TR}}(x)=\dfrac{B(x)}{B(K)}=\dfrac{1-( 1+x)^{-\alpha }}{ 1-( 1+K)^{-\alpha }},\quad 0\lt x\lt K, \\ \overline{B_{K}^{{\rm TR}}}(x) =1-B_{K}^{{\rm TR}}(x)=1-\dfrac{1-( 1+x)^{-\alpha }}{1-( 1+K)^{-\alpha }},\quad 0\lt x\lt K, \\ b_{K}^{{\rm TR}}(x)=\dfrac{d}{dx}B_{K}^{{\rm TR}}(x)=\dfrac{\alpha ( {1+x})^{-{\alpha -1}}}{1-( 1+K)^{-\alpha }},\quad 0\lt x\lt K\text{.} \end{array}\right\} \end{equation}2.4. The expected value of the right-truncated Pareto(II) at level  $K$
$K$
For all ![]() $\alpha \in ( 0,1]$,
$\alpha \in ( 0,1]$, ![]() $Z_{K}^{\textrm {TR}}$ has a finite mean which is given in formulas (3), when using
$Z_{K}^{\textrm {TR}}$ has a finite mean which is given in formulas (3), when using ![]() $\overline {B_{K}^{\textrm {TR}}}(x)$ in (2).
$\overline {B_{K}^{\textrm {TR}}}(x)$ in (2).
 \begin{equation} \left.\begin{aligned} E(Z_{K}^{{\rm TR}}) & =\int_{x=0}^{K}\overline{B_{K}^{{\rm TR}}}(x)\,dx=\int_{x=0}^{K}\left( 1-\dfrac{1-( 1+x)^{-\alpha }}{1-( 1+K)^{-\alpha }} \right) dx \\ & = \int_{x=0}^{K}\left( \dfrac{( 1+x)^{-\alpha }-( 1+K)^{-\alpha }}{1-( 1+K)^{-\alpha }}\right) dx\\ & = K-\dfrac{( -\alpha +1) K-( 1+K)^{-\alpha +1}+1}{ ( -\alpha +1) ( 1-( 1+K)^{-\alpha }) },\quad \text{if }0\lt\alpha \lt1; \\ E(Z_{K}^{{\rm TR}}) & =\left(1+\dfrac{1}{K}\right)\ln (1+K)-1,\quad \text{if }\alpha =1. \end{aligned}\right\} \end{equation}
\begin{equation} \left.\begin{aligned} E(Z_{K}^{{\rm TR}}) & =\int_{x=0}^{K}\overline{B_{K}^{{\rm TR}}}(x)\,dx=\int_{x=0}^{K}\left( 1-\dfrac{1-( 1+x)^{-\alpha }}{1-( 1+K)^{-\alpha }} \right) dx \\ & = \int_{x=0}^{K}\left( \dfrac{( 1+x)^{-\alpha }-( 1+K)^{-\alpha }}{1-( 1+K)^{-\alpha }}\right) dx\\ & = K-\dfrac{( -\alpha +1) K-( 1+K)^{-\alpha +1}+1}{ ( -\alpha +1) ( 1-( 1+K)^{-\alpha }) },\quad \text{if }0\lt\alpha \lt1; \\ E(Z_{K}^{{\rm TR}}) & =\left(1+\dfrac{1}{K}\right)\ln (1+K)-1,\quad \text{if }\alpha =1. \end{aligned}\right\} \end{equation}In (3), ![]() $0\lt E(Z_{K}^{\textrm {TR}})\lt K$ (finite) when
$0\lt E(Z_{K}^{\textrm {TR}})\lt K$ (finite) when ![]() $K\gt0$. (Note: When
$K\gt0$. (Note: When ![]() $\alpha =1$,
$\alpha =1$, ![]() $\inf E(Z_{K}^{\textrm {TR}})=\inf _{K\downarrow 0}E(Z_{K}^{\textrm {TR}})=0$). Thus, the limiting pdfs of excess, age, and total life in
$\inf E(Z_{K}^{\textrm {TR}})=\inf _{K\downarrow 0}E(Z_{K}^{\textrm {TR}})=0$). Thus, the limiting pdfs of excess, age, and total life in ![]() $\{Z_{K\!,n}^{\textrm {TR}}\}_{n=1,2,\ldots }$ exist as time
$\{Z_{K\!,n}^{\textrm {TR}}\}_{n=1,2,\ldots }$ exist as time ![]() $\rightarrow \infty$ (Section 2.5).
$\rightarrow \infty$ (Section 2.5).
We explore using the limiting pdfs of ![]() $\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$ to approximate the analytic fixed finite time
$\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$ to approximate the analytic fixed finite time ![]() $t$ pdfs of excess, age, and total life for large
$t$ pdfs of excess, age, and total life for large ![]() $t$ in the extreme renewal process
$t$ in the extreme renewal process ![]() $\{Z_{n}\}_{{n=1,2,\ldots }}$. When constructing the renewal process
$\{Z_{n}\}_{{n=1,2,\ldots }}$. When constructing the renewal process ![]() $\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$ we will need to determine the value of a right truncation point
$\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$ we will need to determine the value of a right truncation point ![]() $K$ such that the limiting pdfs of excess, age, and total life approximate the corresponding analytic fixed finite time
$K$ such that the limiting pdfs of excess, age, and total life approximate the corresponding analytic fixed finite time ![]() $t$ pdfs in
$t$ pdfs in ![]() $\{Z_{n}\}_{n=1,2,\ldots }$ on a nontrivial subset of the interval
$\{Z_{n}\}_{n=1,2,\ldots }$ on a nontrivial subset of the interval ![]() $( 0,K)$ (Section 4). The quality of the approximation will be measured by an
$( 0,K)$ (Section 4). The quality of the approximation will be measured by an ![]() $L_{1}$ distance measure between the analytic fixed finite time
$L_{1}$ distance measure between the analytic fixed finite time ![]() $t$ pdfs in
$t$ pdfs in ![]() $\{Z_{n}\}_{n=1,2,\ldots }$ and the corresponding (approximating) limiting pdfs in
$\{Z_{n}\}_{n=1,2,\ldots }$ and the corresponding (approximating) limiting pdfs in ![]() $\{Z_{K\!,n}^{\textrm {TR}} \}_{{n=1,2,\ldots }}$ (Section 5).
$\{Z_{K\!,n}^{\textrm {TR}} \}_{{n=1,2,\ldots }}$ (Section 5).
2.5. The limiting pdfs of excess, age, and total life in the renewal process with right-truncated inter-renewals  ${\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}}$
${\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}}$
Denote the limiting excess, age, and total life by ![]() $\gamma _{K}^{\textrm {TR}}$,
$\gamma _{K}^{\textrm {TR}}$, ![]() $\delta _{K}^{\textrm {TR}}$, and
$\delta _{K}^{\textrm {TR}}$, and ![]() $\beta _{K}^{\textrm {TR}}$, respectively; with corresponding pdfs
$\beta _{K}^{\textrm {TR}}$, respectively; with corresponding pdfs ![]() $f_{\gamma _{{K}}}^{\textrm {TR}}(x)$,
$f_{\gamma _{{K}}}^{\textrm {TR}}(x)$, ![]() $0\lt x\lt K$;
$0\lt x\lt K$; ![]() $f_{\delta _{K}}^{\textrm {TR}}(x)$,
$f_{\delta _{K}}^{\textrm {TR}}(x)$, ![]() $0\lt x\lt t$;
$0\lt x\lt t$; ![]() $f_{\beta _{K}}^{\textrm {TR}}(x)$,
$f_{\beta _{K}}^{\textrm {TR}}(x)$, ![]() $0\lt x\lt K$, where
$0\lt x\lt K$, where ![]() $K\gt t$. We use the well-known formulas for the limiting pdfs of a standard renewal process where the inter-renewals have a finite mean (e.g., formulas (6.2), (6.5) and (6.6), pp. 193–194, in [Reference Karlin and Taylor11]) and substitute from the formulas in (2). This gives for the renewal process
$K\gt t$. We use the well-known formulas for the limiting pdfs of a standard renewal process where the inter-renewals have a finite mean (e.g., formulas (6.2), (6.5) and (6.6), pp. 193–194, in [Reference Karlin and Taylor11]) and substitute from the formulas in (2). This gives for the renewal process ![]() $\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$:
$\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$:
 \begin{align} f_{\beta_{K}}^{{\rm TR}}(x)& =\frac{1}{E[ Z_{K_{\beta }}^{{\rm TR}}] } xb_{K_{\beta }}^{{\rm TR}}(x)=\frac{1}{E[ Z_{K_{\beta }}^{{\rm TR}}] }x\left( \frac{\alpha ( {1+x})^{-{\alpha -1}}}{1-( 1+K_{\beta })^{-\alpha }}\right),\quad x\in ( 0,K_{\beta }),\ K_{\beta }\gt t, \end{align}
\begin{align} f_{\beta_{K}}^{{\rm TR}}(x)& =\frac{1}{E[ Z_{K_{\beta }}^{{\rm TR}}] } xb_{K_{\beta }}^{{\rm TR}}(x)=\frac{1}{E[ Z_{K_{\beta }}^{{\rm TR}}] }x\left( \frac{\alpha ( {1+x})^{-{\alpha -1}}}{1-( 1+K_{\beta })^{-\alpha }}\right),\quad x\in ( 0,K_{\beta }),\ K_{\beta }\gt t, \end{align}where ![]() $E[ Z_{K\zeta }^{\textrm {TR}}]$ is given in (3) on replacing
$E[ Z_{K\zeta }^{\textrm {TR}}]$ is given in (3) on replacing ![]() $K$ by
$K$ by ![]() $K_{\zeta }$, where
$K_{\zeta }$, where ![]() $\zeta =\gamma$,
$\zeta =\gamma$, ![]() $\delta$, or
$\delta$, or ![]() $\beta$.
$\beta$.
We can quickly check formulas (4)–(6) using the elementary renewal theorem (e.g., [Reference Ross16] pp. 432–433) and the renewal reward theorem (e.g., [Reference Tijms21] p. 33ff). Note that the sample paths of all three regenerative processes have the same rate out of level ![]() $0$ (see Figure 2), and have the same expected cycle, for example,
$0$ (see Figure 2), and have the same expected cycle, for example, ![]() $E [ Z_{K_{\zeta }}^{\textrm {TR}}]$. That is, by the elementary renewal theorem the rate out of level
$E [ Z_{K_{\zeta }}^{\textrm {TR}}]$. That is, by the elementary renewal theorem the rate out of level ![]() $0$ is
$0$ is ![]() $1/E[ Z_{K\zeta }^{\textrm {TR}}]$,
$1/E[ Z_{K\zeta }^{\textrm {TR}}]$, ![]() $\zeta =\gamma$,
$\zeta =\gamma$, ![]() $\delta$.
$\delta$. ![]() $\beta$ and all three regenerative cycles are equal.
$\beta$ and all three regenerative cycles are equal.

Figure 2. In figure ![]() $Z_{n} \overset {d}{=}Z_{K_{ \varsigma }}^{\textrm {TR}}$,
$Z_{n} \overset {d}{=}Z_{K_{ \varsigma }}^{\textrm {TR}}$, ![]() $\varsigma = \gamma, \delta, \beta$.
$\varsigma = \gamma, \delta, \beta$. ![]() $\gamma _{Z}(t)$ (slope
$\gamma _{Z}(t)$ (slope ![]() $-1$) := limiting excess.
$-1$) := limiting excess. ![]() $\delta _{Z}(t)$ (slope
$\delta _{Z}(t)$ (slope ![]() $+1$) := limiting age.
$+1$) := limiting age. ![]() $\beta _{Z}(t)$ (slope
$\beta _{Z}(t)$ (slope ![]() $0$) := limiting total life. Expected regenerative cycles
$0$) := limiting total life. Expected regenerative cycles ![]() $E[ Z_{K \zeta }^{\textrm {TR}}]$ are all equal.
$E[ Z_{K \zeta }^{\textrm {TR}}]$ are all equal.
Clarifying formula (4), the limiting pdf of excess at time ![]() $t$ (same as the limiting pdf of remaining service time at instant
$t$ (same as the limiting pdf of remaining service time at instant ![]() $t$ (see Figure 2)). The expected number of upcrossings of arbitrary state-space level
$t$ (see Figure 2)). The expected number of upcrossings of arbitrary state-space level ![]() $x$, (
$x$, (![]() $0\lt x\lt K$) in a regenerative cycle is equal to
$0\lt x\lt K$) in a regenerative cycle is equal to ![]() $1$ with probability
$1$ with probability ![]() $\overline {B_{K_{\gamma }}^{\textrm {TR}}}(x)$ (probability that an upward jump representing a service time overshoots level
$\overline {B_{K_{\gamma }}^{\textrm {TR}}}(x)$ (probability that an upward jump representing a service time overshoots level ![]() $x$). By the renewal reward theorem (first two equalities immediately below) and the basic level crossing theorem (third equality immediately below [Reference Brill3]):
$x$). By the renewal reward theorem (first two equalities immediately below) and the basic level crossing theorem (third equality immediately below [Reference Brill3]):
 $$\frac{E[ \text{No. of }x\text{-upcrossings in cycle}] }{E[ \text{cycle}] }=\frac{\overline{B_{K_{\gamma }}^{{\rm TR}}}(x)}{E[ Z_{K_{\gamma }}^{{\rm TR}}] }=\lim_{s\rightarrow \infty }\frac{\mathcal{D}_{s}(x)}{s}=f_{\gamma_{K}}^{{\rm TR}}(x),\quad 0\lt x\lt K_{\gamma },$$
$$\frac{E[ \text{No. of }x\text{-upcrossings in cycle}] }{E[ \text{cycle}] }=\frac{\overline{B_{K_{\gamma }}^{{\rm TR}}}(x)}{E[ Z_{K_{\gamma }}^{{\rm TR}}] }=\lim_{s\rightarrow \infty }\frac{\mathcal{D}_{s}(x)}{s}=f_{\gamma_{K}}^{{\rm TR}}(x),\quad 0\lt x\lt K_{\gamma },$$where ![]() $\mathcal {D}_{s}(x)$ is the number of sample-path downcrossings of level
$\mathcal {D}_{s}(x)$ is the number of sample-path downcrossings of level ![]() $x$ during a time interval
$x$ during a time interval ![]() $( 0,s)$.
$( 0,s)$.
The age at time ![]() $t$ is the time that a customer has been in service at instant
$t$ is the time that a customer has been in service at instant ![]() $t$ (Figure 2). The sample path of the regenerative process for limiting age at
$t$ (Figure 2). The sample path of the regenerative process for limiting age at ![]() $t$ overlays the sample path of the limiting excess at time
$t$ overlays the sample path of the limiting excess at time ![]() $t$. Using the renewal reward theorem and basic LC theorem similarly as for the limiting excess at time
$t$. Using the renewal reward theorem and basic LC theorem similarly as for the limiting excess at time ![]() $t$ yields the formula
$t$ yields the formula
 $$\frac{\overline{B_{K_{\delta }}^{{\rm TR}}}(x)}{E[ Z_{K_{\delta }}^{{\rm TR}}] }=\lim_{s\rightarrow \infty }\frac{\mathcal{U}_{s}(x)}{s}=f_{\delta_{K}}^{{\rm TR}}(x),\quad 0\lt x\lt K_{\delta},$$
$$\frac{\overline{B_{K_{\delta }}^{{\rm TR}}}(x)}{E[ Z_{K_{\delta }}^{{\rm TR}}] }=\lim_{s\rightarrow \infty }\frac{\mathcal{U}_{s}(x)}{s}=f_{\delta_{K}}^{{\rm TR}}(x),\quad 0\lt x\lt K_{\delta},$$where ![]() $\mathcal {U}_{s}(x)$ is the number of sample path upcrossings of level
$\mathcal {U}_{s}(x)$ is the number of sample path upcrossings of level ![]() $x$ during time interval
$x$ during time interval ![]() $( 0,s)$.
$( 0,s)$.
The limiting total life at time ![]() $t$ is equal to limiting excess
$t$ is equal to limiting excess ![]() $+$ limiting age. It is constant during the service time of the customer in service at time
$+$ limiting age. It is constant during the service time of the customer in service at time ![]() $t$. It is also a regenerative process (Figure 2). The sample path of limiting total life overlays the sample paths of the limiting excess and limiting age. The renewal reward theorem gives:
$t$. It is also a regenerative process (Figure 2). The sample path of limiting total life overlays the sample paths of the limiting excess and limiting age. The renewal reward theorem gives:
 $$\frac{\overline{B_{K_{\beta }}^{{\rm TR}}}(x)}{E[ Z_{K_{\beta }}^{{\rm TR}}] } =\lim_{t\rightarrow \infty }\frac{\mathcal{U}_{t}(x)}{t}=\lim_{t\rightarrow \infty }\frac{\mathcal{D}_{t}(x)}{t}=\int_{y=x}^{K}\frac{1}{y} f_{\beta_{K}}^{{\rm TR}}(y)\,dy,\quad 0\lt x\lt K_{\beta }.$$
$$\frac{\overline{B_{K_{\beta }}^{{\rm TR}}}(x)}{E[ Z_{K_{\beta }}^{{\rm TR}}] } =\lim_{t\rightarrow \infty }\frac{\mathcal{U}_{t}(x)}{t}=\lim_{t\rightarrow \infty }\frac{\mathcal{D}_{t}(x)}{t}=\int_{y=x}^{K}\frac{1}{y} f_{\beta_{K}}^{{\rm TR}}(y)\,dy,\quad 0\lt x\lt K_{\beta }.$$Taking ![]() $d/dx$ in the left-most and right-most terms in the immediately-above formula gives
$d/dx$ in the left-most and right-most terms in the immediately-above formula gives
 $$-\frac{b_{K_{\beta }}^{{\rm TR}}(x)}{E[ Z_{K_{\delta }}^{{\rm TR}}] }={-}\frac{1 }{x}f_{\beta_{K}}^{{\rm TR}}(x),\quad 0\lt x\lt K_{\beta },$$
$$-\frac{b_{K_{\beta }}^{{\rm TR}}(x)}{E[ Z_{K_{\delta }}^{{\rm TR}}] }={-}\frac{1 }{x}f_{\beta_{K}}^{{\rm TR}}(x),\quad 0\lt x\lt K_{\beta },$$or
 $$f_{\beta_{K}}^{{\rm TR}}(x)=\frac{xb_{K_{\beta }}^{{\rm TR}}(x)}{E[ Z_{K_{\delta }}^{{\rm TR}}] },\quad 0\lt x\lt K_{\beta }.$$
$$f_{\beta_{K}}^{{\rm TR}}(x)=\frac{xb_{K_{\beta }}^{{\rm TR}}(x)}{E[ Z_{K_{\delta }}^{{\rm TR}}] },\quad 0\lt x\lt K_{\beta }.$$3. Underlying regenerative process and its limiting mixed pdf  ${\{ \pi _{\textrm {RG},0}^{(t)},f_{\textrm {RG}}^{(t)}(x)\}_{0\lt x\lt t}}$
${\{ \pi _{\textrm {RG},0}^{(t)},f_{\textrm {RG}}^{(t)}(x)\}_{0\lt x\lt t}}$
Construct a sample path of the regenerative process ![]() $\{ X_{\textrm {RG}}(s)\}_{s\geq 0}$ with state space
$\{ X_{\textrm {RG}}(s)\}_{s\geq 0}$ with state space ![]() $[0,\infty )$ having a threshold at the fixed finite level of interest
$[0,\infty )$ having a threshold at the fixed finite level of interest ![]() $t$. The sample path is built of i.i.d. probabilistic replicas of the extreme renewal process
$t$. The sample path is built of i.i.d. probabilistic replicas of the extreme renewal process ![]() $\{ Z_{n}\}_{n=1,\ldots,N_{t}}$ (Figure 3).
$\{ Z_{n}\}_{n=1,\ldots,N_{t}}$ (Figure 3).

Figure 3. Sample path of underlying regenerative process ![]() $\{X_{{\rm RG}}(s)\}_{S\geq 0}$ with i.i.d. renewal processes
$\{X_{{\rm RG}}(s)\}_{S\geq 0}$ with i.i.d. renewal processes ![]() $\{ Z_{n}\}_{n=1,2,\ldots}$ in the vertical direction within the horizontal regenerative cycles. When an inter-renewal jumps over level
$\{ Z_{n}\}_{n=1,2,\ldots}$ in the vertical direction within the horizontal regenerative cycles. When an inter-renewal jumps over level ![]() $t$ it “double jumps” immediately down to level 0, beginning a new regenerative cycle. The
$t$ it “double jumps” immediately down to level 0, beginning a new regenerative cycle. The ![]() $a_{i}$s are the times between vertical jumps. The vertical-jump sizes are inter-renewal times. The
$a_{i}$s are the times between vertical jumps. The vertical-jump sizes are inter-renewal times. The ![]() $a_{i}$s are
$a_{i}$s are ![]() $\overset{ d}{=} {\rm Exp}_{1}$ random variables, where
$\overset{ d}{=} {\rm Exp}_{1}$ random variables, where ![]() ${\rm Exp}_{\mu }$ is an exponential random variable with rate
${\rm Exp}_{\mu }$ is an exponential random variable with rate ![]() $\mu$. Also shows SP (system point—leading point of the sample path).
$\mu$. Also shows SP (system point—leading point of the sample path).
The properties of the sample path of ![]() $\{ X_{\textrm {RG}}(s)\}_{s\geq 0}$ are: (1)
$\{ X_{\textrm {RG}}(s)\}_{s\geq 0}$ are: (1) ![]() $X(0)=0$; (2) SP (system point—leading point of the sample path which can jump vertically in the state space, for example, “not in Time”; see Chapter 2 in [Reference Brill5]) makes upward jumps
$X(0)=0$; (2) SP (system point—leading point of the sample path which can jump vertically in the state space, for example, “not in Time”; see Chapter 2 in [Reference Brill5]) makes upward jumps ![]() $\overset {d}{=}Z$ (Pareto(II) variate with shape parameter
$\overset {d}{=}Z$ (Pareto(II) variate with shape parameter ![]() $\alpha \in ( 0,1]$) at an arbitrary Poisson rate
$\alpha \in ( 0,1]$) at an arbitrary Poisson rate ![]() $1/a$ (we select
$1/a$ (we select ![]() $a$ :=
$a$ := ![]() $1$ for simplicity). (3) Whenever a sample-path upward jump upcrosses level
$1$ for simplicity). (3) Whenever a sample-path upward jump upcrosses level ![]() $t$, the sample path of
$t$, the sample path of ![]() $\{ X_{\textrm {RG}}(s)\}_{s\geq 0}$ is prescribed to jump downward instantaneously into level
$\{ X_{\textrm {RG}}(s)\}_{s\geq 0}$ is prescribed to jump downward instantaneously into level ![]() $0$, completing a regenerative cycle, and immediately beginning a new independent regenerative cycle. (4) The sample path on each regenerative cycle is a nondecreasing random step function starting at level
$0$, completing a regenerative cycle, and immediately beginning a new independent regenerative cycle. (4) The sample path on each regenerative cycle is a nondecreasing random step function starting at level ![]() $0$ during every cycle. (5) The sample path's structure rotates the time axis of the extreme renewal process
$0$ during every cycle. (5) The sample path's structure rotates the time axis of the extreme renewal process ![]() $\{ Z_{n}\}_{n=1,2,\ldots }$ in Figure 3 by
$\{ Z_{n}\}_{n=1,2,\ldots }$ in Figure 3 by ![]() $90^{\circ }$ counterclockwise. This construction results in a sequence of adjoining independent realizations of
$90^{\circ }$ counterclockwise. This construction results in a sequence of adjoining independent realizations of ![]() $\{ Z_{n}\}_{n=1,2,\ldots }$ comprising the regenerative cycles (see [Reference Brill4]; also discussed in Section 10.3.1 in [Reference Brill5]).
$\{ Z_{n}\}_{n=1,2,\ldots }$ comprising the regenerative cycles (see [Reference Brill4]; also discussed in Section 10.3.1 in [Reference Brill5]).
The process ![]() $\{X_{\textrm {RG}}(s)\}_{{s\geq 0}}$ has a key limiting mixed pdf (e.g., [Reference Sigman and Wolff18,Reference Smith20]). The limiting mixed pdf is denoted by
$\{X_{\textrm {RG}}(s)\}_{{s\geq 0}}$ has a key limiting mixed pdf (e.g., [Reference Sigman and Wolff18,Reference Smith20]). The limiting mixed pdf is denoted by ![]() $\{ \pi _{\textrm {RG},0}^{(t)},f_{\textrm {RG}}^{(t)}(x)\}_{0\lt x\lt t}$, where
$\{ \pi _{\textrm {RG},0}^{(t)},f_{\textrm {RG}}^{(t)}(x)\}_{0\lt x\lt t}$, where ![]() $\pi _{\textrm {RG},0}^{(t)}:=\lim _{s\rightarrow \infty }P(X_{\textrm {RG}}(s)=0)$ and
$\pi _{\textrm {RG},0}^{(t)}:=\lim _{s\rightarrow \infty }P(X_{\textrm {RG}}(s)=0)$ and ![]() $f_{\textrm {RG}}^{(t)}(x),\ 0\lt x\lt t$, is the absolutely continuous part.
$f_{\textrm {RG}}^{(t)}(x),\ 0\lt x\lt t$, is the absolutely continuous part.
The limiting mixed pdf ![]() $\{ \pi _{\textrm {RG},0}^{(t)},f_{\textrm {RG}}^{(t)}(x)\}_{0\lt x\lt t}$ is the time-average limiting pdf. It is the same as the limiting pdf at the sample-path upward jump instants due to the prescribed Poisson arrivals of renewal upward jumps, by the PASTA principle (Poisson Arrivals See Time Averages, Wolff [Reference Wolff22]). The limiting cdf of
$\{ \pi _{\textrm {RG},0}^{(t)},f_{\textrm {RG}}^{(t)}(x)\}_{0\lt x\lt t}$ is the time-average limiting pdf. It is the same as the limiting pdf at the sample-path upward jump instants due to the prescribed Poisson arrivals of renewal upward jumps, by the PASTA principle (Poisson Arrivals See Time Averages, Wolff [Reference Wolff22]). The limiting cdf of ![]() $\{X_{\textrm {RG}}(s)\}_{{s\geq 0}}$ as
$\{X_{\textrm {RG}}(s)\}_{{s\geq 0}}$ as ![]() $s\rightarrow \infty$, is
$s\rightarrow \infty$, is
with normalizing condition
The pdf ![]() $\{ \pi _{\textrm {RG},0}^{(t)},f_{\textrm {RG}}^{(t)}(x)\}_{0\lt x\lt t}$ is the basis for deriving integral expressions for the analytic fixed finite time
$\{ \pi _{\textrm {RG},0}^{(t)},f_{\textrm {RG}}^{(t)}(x)\}_{0\lt x\lt t}$ is the basis for deriving integral expressions for the analytic fixed finite time ![]() $t$ pdfs of the excess, age, and total life in the extreme renewal process
$t$ pdfs of the excess, age, and total life in the extreme renewal process ![]() $\{ Z_{n}\}_{n=1,2,\ldots }$. (An advantage of the method used here to derive the integral expressions is: the connection with the sample path of the underlying regenerative process gives concrete meaning to the derivations of the integral expressions.)
$\{ Z_{n}\}_{n=1,2,\ldots }$. (An advantage of the method used here to derive the integral expressions is: the connection with the sample path of the underlying regenerative process gives concrete meaning to the derivations of the integral expressions.)
3.1. Obtaining an integral equation for the key limiting mixed pdf  ${\{ \pi _{{\bf RG},0}^{(t)},f_{{\bf RG}}^{(t)}(x)\}_{0\lt x\lt t}}$ in the underlying regenerative process
${\{ \pi _{{\bf RG},0}^{(t)},f_{{\bf RG}}^{(t)}(x)\}_{0\lt x\lt t}}$ in the underlying regenerative process  ${\{ X_{{\bf RG}}(s)\}_{s\geq 0}}$
${\{ X_{{\bf RG}}(s)\}_{s\geq 0}}$
Applying the stochastic level crossing method in Sections 3.2.1–3.2.2, p. 198, in Brill [Reference Brill4] (or Section 10.3 in [Reference Brill5]), leads to the Volterra integral equation of the second kind for ![]() $f_{\textrm {RG}}^{{(}t{)}}(x)$:
$f_{\textrm {RG}}^{{(}t{)}}(x)$:
and the normalizing condition
Formulas (3.13) and (3.14) in Brill [Reference Brill4] connect the solution of Eqs. (9) and (10) to the classical renewal function ![]() $M(x)$ (e.g., [Reference Karlin and Taylor11] p. 169):
$M(x)$ (e.g., [Reference Karlin and Taylor11] p. 169):
where ![]() $M(t)$ is equal to a series of self-convolutions of the inter-renewal cdf
$M(t)$ is equal to a series of self-convolutions of the inter-renewal cdf ![]() $B(x)$. This series may be time-consuming computationally, and tedious to derive, especially for large
$B(x)$. This series may be time-consuming computationally, and tedious to derive, especially for large ![]() $t$.
$t$.
Therefore, we use a relatively straightforward numerical procedure (Section 3.2) to obtain a computational solution for the pdf ![]() $f_{\textrm {RG}}^{({t})}(x)$,
$f_{\textrm {RG}}^{({t})}(x)$, ![]() $0\lt x\lt t$ by solving integral Eq. (9). This is followed by the application of Eq. (10) to obtain a computational solution for
$0\lt x\lt t$ by solving integral Eq. (9). This is followed by the application of Eq. (10) to obtain a computational solution for ![]() $\pi _{\textrm {RG},0}^{(t)}$. (As a by-product, this also gets a computational solution for
$\pi _{\textrm {RG},0}^{(t)}$. (As a by-product, this also gets a computational solution for ![]() $M(t)$ by virtue of formula (11).)
$M(t)$ by virtue of formula (11).)
This proposed numerical procedure used here is sufficient to gain insight into the approximation of the analytic fixed finite time ![]() $t$ pdfs of excess, age, and total life in the renewal process
$t$ pdfs of excess, age, and total life in the renewal process ![]() $\{ Z_{n}\}_{n=1,2\ldots }$ for large
$\{ Z_{n}\}_{n=1,2\ldots }$ for large ![]() $t$ by applying the corresponding computational limiting pdfs in the companion renewal process
$t$ by applying the corresponding computational limiting pdfs in the companion renewal process ![]() $\{Z_{K\!,n}^{\textrm {TR}} \}_{{n=1,2,\ldots }}$.
$\{Z_{K\!,n}^{\textrm {TR}} \}_{{n=1,2,\ldots }}$.
Section 5 considers a plausible ![]() $L_{1}$ measure of the distance (discrepancy) between these two pdfs for each time-
$L_{1}$ measure of the distance (discrepancy) between these two pdfs for each time-![]() $t$ random variable, and gives a computed numerical value of the corresponding measure of distance.
$t$ random variable, and gives a computed numerical value of the corresponding measure of distance.
(The literature contains various numerical solution techniques to solve Volterra integral equations of the second kind, e.g., [Reference Brunner6,Reference Press and Teukolsky14]—and references therein.)
3.2. Details about solving for the limiting mixed pdf  ${\{ \pi _{{\bf RG},0}^{(t)},f_{{\bf RG},}^{(t)}(x)\}_{x\in (0,t)}}$ of the regenerative process
${\{ \pi _{{\bf RG},0}^{(t)},f_{{\bf RG},}^{(t)}(x)\}_{x\in (0,t)}}$ of the regenerative process  ${\{ X_{{\bf RG}}(s)\}_{s\geq 0}}$
${\{ X_{{\bf RG}}(s)\}_{s\geq 0}}$
We solve Eq. (9) with the normalizing condition (10) to derive ![]() $\{ \pi _{\textrm {RG},0}^{(t)},f_{\textrm {RG},}^{(t)}(x)\}_{x\in (0,t)}$ using directly the Riemann–Stieltjes definition of an integral on a finite interval (e.g., [Reference Apostol1] p. 141). The resulting numerical solution is a step function with respect to a preassigned partition of state-space interval
$\{ \pi _{\textrm {RG},0}^{(t)},f_{\textrm {RG},}^{(t)}(x)\}_{x\in (0,t)}$ using directly the Riemann–Stieltjes definition of an integral on a finite interval (e.g., [Reference Apostol1] p. 141). The resulting numerical solution is a step function with respect to a preassigned partition of state-space interval ![]() $(0,t)$ with a norm
$(0,t)$ with a norm ![]() $h\gt0$. To get a good computational solution for
$h\gt0$. To get a good computational solution for ![]() $\{ \pi _{\textrm {RG},0}^{(t)},f_{\textrm {RG}}^{(t)}(x)\}_{x\in (0,t)}$, we choose small
$\{ \pi _{\textrm {RG},0}^{(t)},f_{\textrm {RG}}^{(t)}(x)\}_{x\in (0,t)}$, we choose small ![]() $h$ such that
$h$ such that ![]() $t = Nh$ where
$t = Nh$ where ![]() $N$ is a positive integer.
$N$ is a positive integer.
3.2.1. Use of Pareto(II) shape parameter  $\alpha = 0.5$ and large fixed finite time
$\alpha = 0.5$ and large fixed finite time  ${t}={400}$
${t}={400}$
In the remainder of this paper, we consider a generic case where the shape parameter ![]() $\alpha$ of the Pareto(II)-distributed inter-renewals of the process
$\alpha$ of the Pareto(II)-distributed inter-renewals of the process ![]() $\{ Z_{n}\}_{n=1,2,\ldots }$ is
$\{ Z_{n}\}_{n=1,2,\ldots }$ is ![]() $\alpha = 0.5$ and the “large fixed finite time of interest” is
$\alpha = 0.5$ and the “large fixed finite time of interest” is ![]() $t := 400$, unless otherwise stated. These values help to increase insight in approximating the analytic fixed finite time
$t := 400$, unless otherwise stated. These values help to increase insight in approximating the analytic fixed finite time ![]() $t$ pdfs of excess, age, and total life for large
$t$ pdfs of excess, age, and total life for large ![]() $t$ in the renewal process
$t$ in the renewal process ![]() $\{ Z_{n}\}_{n=1,2\ldots }$ by using the limiting pdfs in the companion renewal process
$\{ Z_{n}\}_{n=1,2\ldots }$ by using the limiting pdfs in the companion renewal process ![]() $\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$, given in formulas (4)–(6) in Section 2.5.
$\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$, given in formulas (4)–(6) in Section 2.5.
3.2.2. Details about computer program to compute limiting mixed pdf  $\{ \pi _{\textrm {RG},0}^{(t)},f_{\textrm {RG},}^{(t)}(x)\}_{x\in (0,t)}$ of the regenerative process
$\{ \pi _{\textrm {RG},0}^{(t)},f_{\textrm {RG},}^{(t)}(x)\}_{x\in (0,t)}$ of the regenerative process  $\{ X_{\textrm {RG}}(s)\}_{s\geq 0}$
$\{ X_{\textrm {RG}}(s)\}_{s\geq 0}$
Let ![]() $f_{\textrm {RG}\ast }^{(t)}(x) ={f_{\textrm {RG}}^{({t})}(x)}/{\pi _{\textrm {RG},0}^{(t)}}$,
$f_{\textrm {RG}\ast }^{(t)}(x) ={f_{\textrm {RG}}^{({t})}(x)}/{\pi _{\textrm {RG},0}^{(t)}}$, ![]() $x\in (0,t)$. This transforms Eq. (9) into the following integral equation for
$x\in (0,t)$. This transforms Eq. (9) into the following integral equation for ![]() $f_{\textrm {RG}\ast }^{({t})}(x)$:
$f_{\textrm {RG}\ast }^{({t})}(x)$:
The computation consists of the following five steps.
Step 1. Compute and store in computer memory:
(13) \begin{equation} b(ih):=\alpha (1+ih)^{{-\alpha -1}},\quad i=0,\ldots,N,\ h\gt0. \end{equation}
\begin{equation} b(ih):=\alpha (1+ih)^{{-\alpha -1}},\quad i=0,\ldots,N,\ h\gt0. \end{equation}Step 2. Using Eq. (12), start the computation with
 $i=0$, that is,
(14)Compute for
$i=0$, that is,
(14)Compute for \begin{equation} f_{{\rm RG}\ast }^{({t})}(x)=b(0)+0=\alpha,\quad 0\lt x\lt h. \end{equation}
\begin{equation} f_{{\rm RG}\ast }^{({t})}(x)=b(0)+0=\alpha,\quad 0\lt x\lt h. \end{equation} $i = 1,\ldots,N$,
(15)where
$i = 1,\ldots,N$,
(15)where \begin{align} f_{{\rm RG}\ast }^{(t)}(ih)& =\alpha (1+ih)^{{-\alpha -1} }+\int_{y=0}^{ih}\alpha (1+ih-y)^{{-\alpha -1}}f_{{\rm RG}\ast }^{(t)}(y)\,dy \nonumber\\ & =\alpha (1+ih)^{{-\alpha -1}}+\sum_{j=1}^{i}\int _{y=(j-1)h}^{jh}\alpha (1+ih-y)^{{-\alpha -1}}f_{{\rm RG}\ast }^{(t)}(y)\,dy,\quad i=1,\ldots,N. \end{align}
\begin{align} f_{{\rm RG}\ast }^{(t)}(ih)& =\alpha (1+ih)^{{-\alpha -1} }+\int_{y=0}^{ih}\alpha (1+ih-y)^{{-\alpha -1}}f_{{\rm RG}\ast }^{(t)}(y)\,dy \nonumber\\ & =\alpha (1+ih)^{{-\alpha -1}}+\sum_{j=1}^{i}\int _{y=(j-1)h}^{jh}\alpha (1+ih-y)^{{-\alpha -1}}f_{{\rm RG}\ast }^{(t)}(y)\,dy,\quad i=1,\ldots,N. \end{align} $f_{\textrm {RG}\ast }^{(t)}(y) = f_{\textrm {RG}\ast }^{(t)}(( i-1) h)$,
$f_{\textrm {RG}\ast }^{(t)}(y) = f_{\textrm {RG}\ast }^{(t)}(( i-1) h)$,  $( i-1) h\lt y\lt ih,$
$( i-1) h\lt y\lt ih,$  $i = 1,\ldots,N$.
$i = 1,\ldots,N$.
This gives the values of
 $f_{\textrm {RG}\ast }^{(t)}(ih),$
$f_{\textrm {RG}\ast }^{(t)}(ih),$  $i =1,\ldots,N$.
$i =1,\ldots,N$.Step 3. From Step 2, construct the step function
(16) \begin{equation} f_{{\rm RG}\ast }^{(t)}(x)=f_{{\rm RG}\ast }^{(t)}((i-1)h),\quad x\in ( ( i-1) h,ih) ,\quad i=1,\ldots,N. \end{equation}
\begin{equation} f_{{\rm RG}\ast }^{(t)}(x)=f_{{\rm RG}\ast }^{(t)}((i-1)h),\quad x\in ( ( i-1) h,ih) ,\quad i=1,\ldots,N. \end{equation}Step 4. Compute the estimation for
(17) \begin{equation} \int_{x=0}^{t}f_{{\rm RG}\ast }^{(t)}(x)\,dx\approx h\sum_{i=1}^{N}f_{{\rm RG}\ast }^{(t)}(ih). \end{equation}
\begin{equation} \int_{x=0}^{t}f_{{\rm RG}\ast }^{(t)}(x)\,dx\approx h\sum_{i=1}^{N}f_{{\rm RG}\ast }^{(t)}(ih). \end{equation}Step 5. Denote the computational solution for
 $\{ \pi _{\textrm {RG},0}^{(t)},f_{\textrm {RG}}^{(t)}(x)\}_{x\in (0,t)}$ by
$\{ \pi _{\textrm {RG},0}^{(t)},f_{\textrm {RG}}^{(t)}(x)\}_{x\in (0,t)}$ by  $\{ \widehat {\pi _{\textrm {RG},0}^{(t)}},\widehat {f_{\textrm {RG}}^{(t)}}(x)\}_{x\in (0,t)}$. Then,
(18)
$\{ \widehat {\pi _{\textrm {RG},0}^{(t)}},\widehat {f_{\textrm {RG}}^{(t)}}(x)\}_{x\in (0,t)}$. Then,
(18) \begin{align} \widehat{f_{{\rm RG}}^{(t)}}(x)& =\widehat{\pi_{{\rm RG},0}^{(t)}} \widehat{f_{{{\rm RG}}\ast }^{(t)}}(x),\quad 0\lt x\lt t, \\ \widehat{\pi_{{\rm RG},0}^{(t)}}+\int_{0}^{t}\widehat{f_{{\rm RG}}^{(t)}}(x)\,dx& = \widehat{\pi_{{\rm RG},0}^{(t)}}+\widehat{\pi_{{\rm RG},0}^{(t)}}\int_{0}^{t}\widehat{ f_{{\rm RG}\ast }^{(t)}}(x)\,dx=1 \nonumber \end{align}(19)giving
\begin{align} \widehat{f_{{\rm RG}}^{(t)}}(x)& =\widehat{\pi_{{\rm RG},0}^{(t)}} \widehat{f_{{{\rm RG}}\ast }^{(t)}}(x),\quad 0\lt x\lt t, \\ \widehat{\pi_{{\rm RG},0}^{(t)}}+\int_{0}^{t}\widehat{f_{{\rm RG}}^{(t)}}(x)\,dx& = \widehat{\pi_{{\rm RG},0}^{(t)}}+\widehat{\pi_{{\rm RG},0}^{(t)}}\int_{0}^{t}\widehat{ f_{{\rm RG}\ast }^{(t)}}(x)\,dx=1 \nonumber \end{align}(19)giving \begin{align} & \approx \widehat{\pi_{{\rm RG},0}^{(t)}}+\widehat{\pi_{{\rm RG},0}^{(t)}} h\sum_{i=1}^{N}\widehat{f_{{\rm RG}\ast }^{(t)}}(ih)\,dx=1, \end{align}(20)
\begin{align} & \approx \widehat{\pi_{{\rm RG},0}^{(t)}}+\widehat{\pi_{{\rm RG},0}^{(t)}} h\sum_{i=1}^{N}\widehat{f_{{\rm RG}\ast }^{(t)}}(ih)\,dx=1, \end{align}(20) \begin{equation} \widehat{\pi_{{\rm RG},0}^{(t)}}\approx \frac{1}{1+h\sum_{i=1}^{N}\widehat{ f_{{\rm RG}\ast }^{(t)}}(ih)}. \end{equation}
\begin{equation} \widehat{\pi_{{\rm RG},0}^{(t)}}\approx \frac{1}{1+h\sum_{i=1}^{N}\widehat{ f_{{\rm RG}\ast }^{(t)}}(ih)}. \end{equation}
To make the computational solutions concrete, we assume, in addition to ![]() $\alpha = 0.5$,
$\alpha = 0.5$, ![]() $t= 400$, that
$t= 400$, that ![]() $h = 0.1$,
$h = 0.1$, ![]() $N = 4000$.
$N = 4000$.
In the sequel, we denote pdfs and related quantities which we derive computationally, by using a “hat”, for example, “![]() $\widehat {\textrm {pdf}}$”. Quantities which are known or derived from theory will not have a “hat”.
$\widehat {\textrm {pdf}}$”. Quantities which are known or derived from theory will not have a “hat”.
The computational mixed pdf ![]() $\{ \widehat {\pi _{\textrm {RG},0}^{(t)}},\widehat { f_{\textrm {RG}}^{(t)}}(x)\} _{0\lt x\lt t}$ is plotted in Figure 4.
$\{ \widehat {\pi _{\textrm {RG},0}^{(t)}},\widehat { f_{\textrm {RG}}^{(t)}}(x)\} _{0\lt x\lt t}$ is plotted in Figure 4.

Figure 4. Computational mixed limiting pdf of the regenerative process ![]() $\{\widehat {\pi _{\textrm {RG},0}^{(t)}}, \widehat {f_{\textrm {RG}}^{(t)}(x)}\}_{{x\in (0,t)}}$ (see Eq. (9)).
$\{\widehat {\pi _{\textrm {RG},0}^{(t)}}, \widehat {f_{\textrm {RG}}^{(t)}(x)}\}_{{x\in (0,t)}}$ (see Eq. (9)). ![]() $\alpha =0.5$,
$\alpha =0.5$, ![]() $t=400$;
$t=400$; ![]() $\widehat {\pi _{\textrm {RG},0}^{(t)}}= 0.072996.$
$\widehat {\pi _{\textrm {RG},0}^{(t)}}= 0.072996.$
The computational solutions can be improved in various ways, for example, making the norm size ![]() $h$ smaller and the corresponding
$h$ smaller and the corresponding ![]() $N$ larger; using trapezoidal areas instead of rectangular areas in intervals
$N$ larger; using trapezoidal areas instead of rectangular areas in intervals ![]() $( (i-1)h,ih)$,
$( (i-1)h,ih)$, ![]() $i = 1,\ldots,N$; etc. (see [Reference Brunner6]). Section 4 displays the analytic fixed finite time
$i = 1,\ldots,N$; etc. (see [Reference Brunner6]). Section 4 displays the analytic fixed finite time ![]() $t$ pdfs of excess, age, and total life in the extreme renewal process
$t$ pdfs of excess, age, and total life in the extreme renewal process ![]() $\{ Z_{n}\}_{n=1,2\ldots }$, with the corresponding limiting pdfs of the companion renewal process
$\{ Z_{n}\}_{n=1,2\ldots }$, with the corresponding limiting pdfs of the companion renewal process ![]() $\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$, given in Section 2.5. (Note: The limiting pdfs are known from theory and do not require any extra computation here.)
$\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$, given in Section 2.5. (Note: The limiting pdfs are known from theory and do not require any extra computation here.)
3.3. Obtaining integral expressions for the analytic fixed finite time  $t$ pdfs in the extreme renewal process
$t$ pdfs in the extreme renewal process  ${\{ Z_{n}\}_{n=1,2,\ldots },0\lt t\lt\infty}$
${\{ Z_{n}\}_{n=1,2,\ldots },0\lt t\lt\infty}$
Using the computational solutions for the mixed pdf ![]() $\{ \widehat {\pi _{\textrm {RG},0}^{(t)}},\widehat {f_{\textrm {RG}}^{(t)}}(x)\}_{0\lt x\lt t}$ of the regenerative process
$\{ \widehat {\pi _{\textrm {RG},0}^{(t)}},\widehat {f_{\textrm {RG}}^{(t)}}(x)\}_{0\lt x\lt t}$ of the regenerative process ![]() $\{ X_{\textrm {RG}}(s)\}_{s\geq 0}$, we create integral expressions of the analytic fixed finite time
$\{ X_{\textrm {RG}}(s)\}_{s\geq 0}$, we create integral expressions of the analytic fixed finite time ![]() $t$ pdfs in
$t$ pdfs in ![]() $\{ Z_{n}\}_{n=1,2\ldots }$.
$\{ Z_{n}\}_{n=1,2\ldots }$.
Denote the analytic fixed finite time ![]() $t$ excess, age, and total life by
$t$ excess, age, and total life by ![]() $\gamma _{t}$,
$\gamma _{t}$, ![]() $\delta _{t}$, and
$\delta _{t}$, and ![]() $\beta _{t}$, respectively, with corresponding pdfs:
$\beta _{t}$, respectively, with corresponding pdfs: ![]() $\widehat {f_{\gamma _{t}}}(x),$
$\widehat {f_{\gamma _{t}}}(x),$ ![]() $0\lt x\lt\infty$;
$0\lt x\lt\infty$; ![]() $\{ \widehat {\pi _{\delta _{t}}},\widehat {f_{\delta _{t}}}(x)\}_{0\lt x\lt t}$ (Note: the atom
$\{ \widehat {\pi _{\delta _{t}}},\widehat {f_{\delta _{t}}}(x)\}_{0\lt x\lt t}$ (Note: the atom ![]() $\widehat {\pi _{\delta _{t}}}\approx P(\delta _{t}=t)$; the computational pdf of total life is denoted by
$\widehat {\pi _{\delta _{t}}}\approx P(\delta _{t}=t)$; the computational pdf of total life is denoted by ![]() $\widehat { f_{\beta _{t}}}(x)$,
$\widehat { f_{\beta _{t}}}(x)$, ![]() $0\lt x\lt\infty$.)
$0\lt x\lt\infty$.)
For each large ![]() $t\gt0$, evaluating the pdf
$t\gt0$, evaluating the pdf ![]() $\{ \widehat {\pi _{\textrm {RG},0}^{(t)}},\widehat {f_{\textrm {RG}}^{(t)}}(x)\}_{0\lt x\lt t}$ may require a time-consuming computational solution of a Volterra integral equation of the second kind, due to the nature of the Pareto(II) distribution. Increasing values of
$\{ \widehat {\pi _{\textrm {RG},0}^{(t)}},\widehat {f_{\textrm {RG}}^{(t)}}(x)\}_{0\lt x\lt t}$ may require a time-consuming computational solution of a Volterra integral equation of the second kind, due to the nature of the Pareto(II) distribution. Increasing values of ![]() $t$ require corresponding increasing computation times.)
$t$ require corresponding increasing computation times.)
Formulas (21)–(23) are obtained from formulas derived in Brill [Reference Brill4]. For example, formula (4.4a) in [Reference Brill4] gives
 \begin{equation} f_{\gamma_{t}}(x)=b(t+x)+\int_{y=0}^{t}b(t+x-y)\frac{f_{{\rm RG}}^{( t) }(y)}{\pi_{{\rm RG},0}^{(t)}}\,dy,\quad 0\lt x\lt\infty. \end{equation}
\begin{equation} f_{\gamma_{t}}(x)=b(t+x)+\int_{y=0}^{t}b(t+x-y)\frac{f_{{\rm RG}}^{( t) }(y)}{\pi_{{\rm RG},0}^{(t)}}\,dy,\quad 0\lt x\lt\infty. \end{equation}Formula (4.11) in [Reference Brill4] gives
 \begin{equation} f_{\delta_{t}}(x)=\bar{B}(x)\frac{f_{{\rm RG}}^{(t)}(t-x)}{\pi_{{\rm RG},0}^{(t)}} ,\quad 0\lt x\lt t;\quad \pi_{\delta_{t}}=\bar{B}(t). \end{equation}
\begin{equation} f_{\delta_{t}}(x)=\bar{B}(x)\frac{f_{{\rm RG}}^{(t)}(t-x)}{\pi_{{\rm RG},0}^{(t)}} ,\quad 0\lt x\lt t;\quad \pi_{\delta_{t}}=\bar{B}(t). \end{equation}The formula for ![]() $f_{\beta _{t}}(x),0\lt x\lt\infty$, is given in formula (4.13) in [Reference Brill4], and also in formula (23) for convenience.
$f_{\beta _{t}}(x),0\lt x\lt\infty$, is given in formula (4.13) in [Reference Brill4], and also in formula (23) for convenience.
 \begin{equation} f_{\beta_{t}}(x)=\left\{\begin{array}{l} \displaystyle b(x)\int_{y=t-x}^{t}\dfrac{f_{{\rm RG}}^{(t)}(y)}{\pi_{{\rm RG}}^{(t)},_{0}}\,dy,\quad 0\lt x\lt t, \\[6pt] \displaystyle b(x)\left( 1+\int_{y=t-x}^{t}\dfrac{f_{{\rm RG}}^{(t)}(y)}{\pi_{{\rm RG},0}^{(t)}} \,dy\right) ,\quad t\leq x\lt\infty. \end{array}\right. \end{equation}
\begin{equation} f_{\beta_{t}}(x)=\left\{\begin{array}{l} \displaystyle b(x)\int_{y=t-x}^{t}\dfrac{f_{{\rm RG}}^{(t)}(y)}{\pi_{{\rm RG}}^{(t)},_{0}}\,dy,\quad 0\lt x\lt t, \\[6pt] \displaystyle b(x)\left( 1+\int_{y=t-x}^{t}\dfrac{f_{{\rm RG}}^{(t)}(y)}{\pi_{{\rm RG},0}^{(t)}} \,dy\right) ,\quad t\leq x\lt\infty. \end{array}\right. \end{equation} The formulas (21)–(23), and those for ![]() $\bar {B}(x)$ and
$\bar {B}(x)$ and ![]() $b(x)$ in formula (1), are valid when the inter-renewals are
$b(x)$ in formula (1), are valid when the inter-renewals are ![]() $\overset {d}{=}$ Pareto(II) variate with shape parameter
$\overset {d}{=}$ Pareto(II) variate with shape parameter ![]() $\alpha \in ( 0,1]$.
$\alpha \in ( 0,1]$.
Remark 1 Formula (22) shows that ![]() $\delta _{t}$ has an atom at level
$\delta _{t}$ has an atom at level ![]() $t$ with probability
$t$ with probability ![]() $\pi _{\delta _{t}} = ( 1+t)^{-\alpha }$. Formula (23) shows that
$\pi _{\delta _{t}} = ( 1+t)^{-\alpha }$. Formula (23) shows that ![]() $f_{\beta _{t}}(x)$ has a discontinuity at level
$f_{\beta _{t}}(x)$ has a discontinuity at level ![]() $x=t$ of size
$x=t$ of size
We obtain computational results for the analytic fixed finite time ![]() $t$ pdfs in formulas (21)–(23) by substituting in them the computational step function
$t$ pdfs in formulas (21)–(23) by substituting in them the computational step function ![]() $\{ \widehat {\pi _{\textrm {RG},0}^{(t)}}, \widehat {f_{\textrm {RG}}^{(t{)}}}(x)\} _{0\lt x\lt t}$ given in formulas (18) and (20) for the pdf of the regenerative process
$\{ \widehat {\pi _{\textrm {RG},0}^{(t)}}, \widehat {f_{\textrm {RG}}^{(t{)}}}(x)\} _{0\lt x\lt t}$ given in formulas (18) and (20) for the pdf of the regenerative process ![]() $\{ \widehat {\pi _{\textrm {RG},0}^{(t)}},\widehat {f_{\textrm {RG}}^{(t {)}}}(x)\}_{0\lt x\lt t}$, where
$\{ \widehat {\pi _{\textrm {RG},0}^{(t)}},\widehat {f_{\textrm {RG}}^{(t {)}}}(x)\}_{0\lt x\lt t}$, where ![]() $t \in (0,\infty )$.
$t \in (0,\infty )$.
The computational analytic fixed finite time ![]() $t$ pdfs in
$t$ pdfs in ![]() $\{ Z_{n}\}_{n=1,2,\ldots }: \widehat {f_{\gamma _{t}}}(x)$,
$\{ Z_{n}\}_{n=1,2,\ldots }: \widehat {f_{\gamma _{t}}}(x)$, ![]() $x\gt0$,
$x\gt0$, ![]() $\{ \widehat {\pi _{\delta _{t}}},\widehat {f_{\delta _{t}}}(x)\}_{0\lt x\lt t}$, and
$\{ \widehat {\pi _{\delta _{t}}},\widehat {f_{\delta _{t}}}(x)\}_{0\lt x\lt t}$, and ![]() $\widehat {f_{\beta _{t}}}(x)$,
$\widehat {f_{\beta _{t}}}(x)$, ![]() $x\gt0$, are specified directly in terms of
$x\gt0$, are specified directly in terms of ![]() $\{ \widehat {\pi _{\textrm {RG},0}^{(t)}},\widehat {f_{\textrm {RG}}^{(t {)}}}(x)\} _{0\lt x\lt t}$ in
$\{ \widehat {\pi _{\textrm {RG},0}^{(t)}},\widehat {f_{\textrm {RG}}^{(t {)}}}(x)\} _{0\lt x\lt t}$ in ![]() $\{ X_{\textrm {RG}}(s)\}_{s\geq 0}$ (Section 3.2.2). Examples of these estimated analytic fixed finite time
$\{ X_{\textrm {RG}}(s)\}_{s\geq 0}$ (Section 3.2.2). Examples of these estimated analytic fixed finite time ![]() $t$ pdfs are plotted in Figures 5, 6, and 7, respectively.
$t$ pdfs are plotted in Figures 5, 6, and 7, respectively.

Figure 5. ![]() $\widehat {f_{ \gamma _{t}}}(x)$,
$\widehat {f_{ \gamma _{t}}}(x)$, ![]() $0\lt x\lt800$,
$0\lt x\lt800$, ![]() $\alpha =0.5$,
$\alpha =0.5$, ![]() $t=400$,
$t=400$, ![]() $h=0.1$,
$h=0.1$, ![]() $N=4000$.
$N=4000$.

Figure 6. ![]() $\{ \widehat {\pi _{\delta _{t}}},\widehat {f_{\delta _{t}}}(x)\} _{0\lt x\lt t}$,
$\{ \widehat {\pi _{\delta _{t}}},\widehat {f_{\delta _{t}}}(x)\} _{0\lt x\lt t}$, ![]() $\alpha =0.5$,
$\alpha =0.5$, ![]() $t=400$,
$t=400$, ![]() $h=0.1$,
$h=0.1$, ![]() $N=4000$.
$N=4000$. ![]() $\widehat {\pi _{\delta _{t}}}=0.049938$.
$\widehat {\pi _{\delta _{t}}}=0.049938$.

Figure 7. ![]() $\widehat {f_{\beta _{t}}}(x)$,
$\widehat {f_{\beta _{t}}}(x)$, ![]() $0\lt x\lt800$,
$0\lt x\lt800$, ![]() $\alpha =0.5$,
$\alpha =0.5$, ![]() $t=400$,
$t=400$, ![]() $h=0.1$,
$h=0.1$, ![]() $N=4000$. Discontinuity at time point
$N=4000$. Discontinuity at time point ![]() $t$ is equal to
$t$ is equal to ![]() $b(t)=\alpha (1+t)^{-\alpha -1}$.
$b(t)=\alpha (1+t)^{-\alpha -1}$.
4. Using limiting pdfs of  ${\{Z_{K\!,n}^{\textrm {TR}} \}_{{n=1,2,\ldots }}}$ to approximate analytic fixed finite time
${\{Z_{K\!,n}^{\textrm {TR}} \}_{{n=1,2,\ldots }}}$ to approximate analytic fixed finite time  $t$ pdfs of
$t$ pdfs of  ${\{Z_{n}\}_{n=1,2,\ldots }}$ (fixed finite large
${\{Z_{n}\}_{n=1,2,\ldots }}$ (fixed finite large  ${t}$)
${t}$)
We use the limiting pdfs ![]() $f_{\zeta _{K}}^{\textrm {TR}}(x)$,
$f_{\zeta _{K}}^{\textrm {TR}}(x)$, ![]() $0\lt x\lt\zeta _{K}$, (
$0\lt x\lt\zeta _{K}$, (![]() $\zeta =\gamma$,
$\zeta =\gamma$, ![]() $\delta$,
$\delta$, ![]() $\beta$) given by formulas (4)–(6) in Section 2.5, to approximate the corresponding analytic fixed finite time
$\beta$) given by formulas (4)–(6) in Section 2.5, to approximate the corresponding analytic fixed finite time ![]() $t$ pdfs
$t$ pdfs ![]() $\widehat {f_{\zeta _{{t}}}}(x)$,
$\widehat {f_{\zeta _{{t}}}}(x)$, ![]() $0\lt x\lt K_{\zeta }$ (
$0\lt x\lt K_{\zeta }$ (![]() $\zeta = \gamma$,
$\zeta = \gamma$, ![]() $\delta,\beta$) in the extreme renewal process
$\delta,\beta$) in the extreme renewal process ![]() $\{Z_{n}\}_{n=1,2,\ldots }$ (
$\{Z_{n}\}_{n=1,2,\ldots }$ (![]() $t$ large). Computing analytic pdfs
$t$ large). Computing analytic pdfs ![]() $\widehat {f_{\zeta _{{t}}}}(x)$,
$\widehat {f_{\zeta _{{t}}}}(x)$, ![]() $\zeta =\gamma$,
$\zeta =\gamma$, ![]() $\delta _{t}$,
$\delta _{t}$, ![]() $\beta _{t}$, for
$\beta _{t}$, for ![]() $\{Z_{n}\}_{n=1,2,\ldots }$ is time-consuming, requiring numerical solutions of Volterra integral equations and related quantities (Section 3.3). This tediousness increases motivation to apply the no-computation well-known limiting pdfs
$\{Z_{n}\}_{n=1,2,\ldots }$ is time-consuming, requiring numerical solutions of Volterra integral equations and related quantities (Section 3.3). This tediousness increases motivation to apply the no-computation well-known limiting pdfs ![]() $f_{\zeta _{K}}^{\textrm {TR}}(x)$s to approximate
$f_{\zeta _{K}}^{\textrm {TR}}(x)$s to approximate ![]() $\widehat {f_{\zeta _{{t}}}}(x)$,
$\widehat {f_{\zeta _{{t}}}}(x)$, ![]() $\zeta =\gamma, \delta, \beta$, (
$\zeta =\gamma, \delta, \beta$, (![]() $t$ large).
$t$ large).
4.1. Selecting right truncation points of the inter-renewals in the renewal process  ${\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}}$
${\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}}$
We derive the right truncation points of the Pareto(II) variate, ![]() $K_{\gamma }$,
$K_{\gamma }$, ![]() $K_{\delta,}$, and
$K_{\delta,}$, and ![]() $K_{\beta }$, which are useful for approximating the fixed finite
$K_{\beta }$, which are useful for approximating the fixed finite ![]() $t$ pdfs of excess, age, and total life, respectively. The resulting right-truncated inter-renewals, denoted by
$t$ pdfs of excess, age, and total life, respectively. The resulting right-truncated inter-renewals, denoted by ![]() $Z_{K_{\gamma }}^{\textrm {TR}}$,
$Z_{K_{\gamma }}^{\textrm {TR}}$, ![]() $Z_{K_{\delta,}}^{\textrm {TR}}$, and
$Z_{K_{\delta,}}^{\textrm {TR}}$, and ![]() $Z_{K_{\beta }}^{\textrm {TR}}$, respectively, have pdfs given by formulas (4)–(6) on interval
$Z_{K_{\beta }}^{\textrm {TR}}$, respectively, have pdfs given by formulas (4)–(6) on interval ![]() $( 0,K_{\zeta })$,
$( 0,K_{\zeta })$, ![]() $\zeta =\gamma, \delta, \beta$. The
$\zeta =\gamma, \delta, \beta$. The ![]() $Z_{K_{\zeta }}^{\textrm {TR}}$s in the renewal process
$Z_{K_{\zeta }}^{\textrm {TR}}$s in the renewal process ![]() $\{Z_{K_{\varsigma },n}^{\textrm {TR}}\}_{n=1,2,\ldots }$have the same shape parameter
$\{Z_{K_{\varsigma },n}^{\textrm {TR}}\}_{n=1,2,\ldots }$have the same shape parameter ![]() $\alpha$ as the Pareto(II) variate in the original extreme renewal process of interest
$\alpha$ as the Pareto(II) variate in the original extreme renewal process of interest ![]() $\{ Z_{n}\} _{n=1,2\ldots }$.
$\{ Z_{n}\} _{n=1,2\ldots }$.
4.2. Details for approximating the analytic fixed finite time pdfs of  ${\gamma _{t}}$,
${\gamma _{t}}$,  ${\delta _{t}}$, and
${\delta _{t}}$, and  ${\beta_{t}}$
${\beta_{t}}$
4.2.1. Details for approximating the pdf of  $\gamma _{t}$
$\gamma _{t}$
Letting ![]() $x\downarrow 0$ in formula (21) gives
$x\downarrow 0$ in formula (21) gives
 \begin{equation} f_{{\gamma }_{t}}(0^{+})=\alpha (1+t)^{-\alpha -1}+\alpha \int_{{y=0}}^{{t}}(1+t-y)^{{-\alpha -1}}\dfrac{ {f}_{{\rm RG}}^{(t)}{(y)}}{{\pi }_{{\rm RG},{0}}^{({t})}}\,dy,\quad 0\lt t\lt\infty. \end{equation}
\begin{equation} f_{{\gamma }_{t}}(0^{+})=\alpha (1+t)^{-\alpha -1}+\alpha \int_{{y=0}}^{{t}}(1+t-y)^{{-\alpha -1}}\dfrac{ {f}_{{\rm RG}}^{(t)}{(y)}}{{\pi }_{{\rm RG},{0}}^{({t})}}\,dy,\quad 0\lt t\lt\infty. \end{equation}Since ![]() $\overline {B_{K_{\gamma }}^{\textrm {TR}}}(0) = 1$ in (4), we equate the values of formula (25) and (4) at
$\overline {B_{K_{\gamma }}^{\textrm {TR}}}(0) = 1$ in (4), we equate the values of formula (25) and (4) at ![]() $x=0^{+}$ and solve for
$x=0^{+}$ and solve for ![]() $K_{\gamma }$ in the equation
$K_{\gamma }$ in the equation
where ![]() $E[ Z_{K\gamma }^{\textrm {TR}}]$ is given in formula (3). The solution of (26) is
$E[ Z_{K\gamma }^{\textrm {TR}}]$ is given in formula (3). The solution of (26) is ![]() $K_{\gamma }$ for the inter-renewals in
$K_{\gamma }$ for the inter-renewals in ![]() $\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$. We shall use the Policy expressed by Eq. (26) for the approximation procedure because it is plausible and of theoretical interest.
$\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$. We shall use the Policy expressed by Eq. (26) for the approximation procedure because it is plausible and of theoretical interest.
When ![]() $t = 400$ (considered here as a large
$t = 400$ (considered here as a large ![]() $t$) and
$t$) and ![]() $\alpha =0.5$, Eq. (26) gives
$\alpha =0.5$, Eq. (26) gives ![]() $K_{\gamma } = 3877.5672$ and
$K_{\gamma } = 3877.5672$ and ![]() $E(Z_{K}^{\textrm {TR}}) = 61.2781$. The right truncation point
$E(Z_{K}^{\textrm {TR}}) = 61.2781$. The right truncation point ![]() $K_{\gamma }$ is significantly greater than
$K_{\gamma }$ is significantly greater than ![]() $t=400$. Pdf
$t=400$. Pdf ![]() $\widehat {f_{\gamma _{t}}}(x)$ versus pdf
$\widehat {f_{\gamma _{t}}}(x)$ versus pdf ![]() $f_{\gamma _{K}}^{\textrm {TR}}(x)$ is plotted in Figure 8. The closeness of the two pdfs appears to be good.
$f_{\gamma _{K}}^{\textrm {TR}}(x)$ is plotted in Figure 8. The closeness of the two pdfs appears to be good.

Figure 8. Analytical time ![]() $t$ pdf of excess
$t$ pdf of excess ![]() $\widehat {f_{\gamma _{t}}}(x)$ (solid blue line) versus approximating pdf
$\widehat {f_{\gamma _{t}}}(x)$ (solid blue line) versus approximating pdf ![]() $f_{\gamma _{K}}^{\textrm {TR}}(x)$ (red line),
$f_{\gamma _{K}}^{\textrm {TR}}(x)$ (red line), ![]() $0\lt x\lt800$.
$0\lt x\lt800$. ![]() $\alpha =0.5$, fixed finite
$\alpha =0.5$, fixed finite ![]() $t=400$.
$t=400$.
4.2.2. Details for approximating the pdf of  $\delta _{t}$
$\delta _{t}$
From the discussion in Section 2.5 and Figure 2, we have
Note that ![]() $K_{\delta }=K_{\gamma }=3877.5672$. In pdf,
$K_{\delta }=K_{\gamma }=3877.5672$. In pdf, ![]() $\{ \widehat {\pi _{\delta _{t}}},\widehat {f_{\delta _{t}}}(x)\}_{0\lt x\lt t}$,
$\{ \widehat {\pi _{\delta _{t}}},\widehat {f_{\delta _{t}}}(x)\}_{0\lt x\lt t}$, ![]() $\widehat { \pi _{\delta _{t}}}\gt0$ is a small probability when
$\widehat { \pi _{\delta _{t}}}\gt0$ is a small probability when ![]() $t$ is large. The absolutely continuous part of the pdf
$t$ is large. The absolutely continuous part of the pdf ![]() $\widehat {f_{\delta _{t}}}(x)$ versus
$\widehat {f_{\delta _{t}}}(x)$ versus ![]() $f_{\delta _{K}}^{\textrm {TR}}(x)$,
$f_{\delta _{K}}^{\textrm {TR}}(x)$, ![]() $0\lt x\lt t$ (
$0\lt x\lt t$ (![]() $t=400)$, is plotted in Figure 9. The closeness between the two pdfs appears to be good on the nontrivial interval
$t=400)$, is plotted in Figure 9. The closeness between the two pdfs appears to be good on the nontrivial interval ![]() $( 0,200)$, the discrepancy increases rapidly on
$( 0,200)$, the discrepancy increases rapidly on ![]() $( 200,400).$
$( 200,400).$

Figure 9. Analytic time ![]() $t$ pdf of
$t$ pdf of ![]() $\widehat {f_{\delta _{t}}}(x)$ (solid blue line) versus
$\widehat {f_{\delta _{t}}}(x)$ (solid blue line) versus ![]() $f_{\delta _{K}}^{\textrm {TR}}(x)$ (red line),
$f_{\delta _{K}}^{\textrm {TR}}(x)$ (red line), ![]() $0\lt x\lt400$.
$0\lt x\lt400$. ![]() $\alpha =0.5$, fixed finite
$\alpha =0.5$, fixed finite ![]() $t=400$.
$t=400$.
4.2.3. Details for approximating the pdf of  $\beta _{t}$
$\beta _{t}$
Using an equation similar to Eq. (26) and letting ![]() $x=0$ gives “
$x=0$ gives “![]() $0=0$”, which does not provide an equation directly for
$0=0$”, which does not provide an equation directly for ![]() $K_{\beta }$. Hence, we will use a plausible
$K_{\beta }$. Hence, we will use a plausible ![]() $K_{\beta }\gt0$. We now compare analytic pdf
$K_{\beta }\gt0$. We now compare analytic pdf ![]() $\widehat {f_{{\beta }_{ {t}}}}(x)$ with the corresponding approximating pdf
$\widehat {f_{{\beta }_{ {t}}}}(x)$ with the corresponding approximating pdf ![]() $f_{\beta _{K}}^{\textrm {TR}}(x)$. When
$f_{\beta _{K}}^{\textrm {TR}}(x)$. When ![]() $t = 400$ and
$t = 400$ and ![]() $\alpha =0.5$, we use
$\alpha =0.5$, we use ![]() $K_{{\beta }} = 3877.5672$; giving
$K_{{\beta }} = 3877.5672$; giving ![]() $E [Z_{{K}_{{\beta }}}] = 61.2781$, the same as for
$E [Z_{{K}_{{\beta }}}] = 61.2781$, the same as for ![]() $K_{\gamma }$ and for
$K_{\gamma }$ and for ![]() $K_{\delta }$. Pdf
$K_{\delta }$. Pdf ![]() $\widehat { f_{{\beta }_{t}}}(x)$ versus limiting pdf
$\widehat { f_{{\beta }_{t}}}(x)$ versus limiting pdf ![]() $f_{{K}_{ {\beta }}}(x)$ is plotted in Figure 10.
$f_{{K}_{ {\beta }}}(x)$ is plotted in Figure 10.

Figure 10. ![]() $\widehat {f_{\beta _{t}}}(x)$ (blue line) versus
$\widehat {f_{\beta _{t}}}(x)$ (blue line) versus ![]() $f_{\beta _{K}}^{\textrm {TR}}(x)$ (red line),
$f_{\beta _{K}}^{\textrm {TR}}(x)$ (red line), ![]() $0\lt x\lt800$.
$0\lt x\lt800$. ![]() $\alpha =0.5$, fixed finite
$\alpha =0.5$, fixed finite ![]() $t=400$.
$t=400$.
5. Measure of distance between the analytic fixed finite time  $t$ pdfs and the limiting pdfs of the renewal process
$t$ pdfs and the limiting pdfs of the renewal process  ${\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}}$
${\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}}$
We quantify the notion: “The limiting pdf ![]() $f_{\zeta _{K}}(\cdot )$ of the renewal process
$f_{\zeta _{K}}(\cdot )$ of the renewal process ![]() $\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$ approximates the analytic fixed finite time
$\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$ approximates the analytic fixed finite time ![]() $t$ pdf
$t$ pdf ![]() $\widehat {f_{\zeta _{t}}} (\cdot )$ for
$\widehat {f_{\zeta _{t}}} (\cdot )$ for ![]() $\zeta = \gamma$,
$\zeta = \gamma$, ![]() $\delta$,
$\delta$, ![]() $\beta$”, by using an
$\beta$”, by using an ![]() $L_{1}$ measure based on the metric
$L_{1}$ measure based on the metric ![]() $\vert \widehat { f_{\zeta _{t}}}(x)-f_{\zeta _{K}}^{\textrm {TR}}(x)\vert$,
$\vert \widehat { f_{\zeta _{t}}}(x)-f_{\zeta _{K}}^{\textrm {TR}}(x)\vert$, ![]() $0\lt x\lt K_{\zeta }$. This metric leads to an integral measure for the distance between the analytic pdfs
$0\lt x\lt K_{\zeta }$. This metric leads to an integral measure for the distance between the analytic pdfs ![]() $\widehat {f_{\zeta _{t}}}(x)$ and the corresponding approximating limiting pdfs
$\widehat {f_{\zeta _{t}}}(x)$ and the corresponding approximating limiting pdfs ![]() $f_{\zeta _{K}}^{\textrm {TR}}(x)$ for
$f_{\zeta _{K}}^{\textrm {TR}}(x)$ for ![]() $x\in ( 0,K_{\zeta })$,
$x\in ( 0,K_{\zeta })$, ![]() $\zeta =\gamma$,
$\zeta =\gamma$, ![]() $\delta$,
$\delta$, ![]() $\beta$.
$\beta$.
5.1. The metric  ${\vert \widehat {f_{ \zeta _{t}}}(x)-f_{\zeta _{K}}^{\textrm {TR}}(x)\vert}$,
${\vert \widehat {f_{ \zeta _{t}}}(x)-f_{\zeta _{K}}^{\textrm {TR}}(x)\vert}$,  ${\zeta =\gamma,\delta,\beta}$
${\zeta =\gamma,\delta,\beta}$
We use a measure of distance (discrepancy) motivated by the areas between the fixed time ![]() $t$ pdfs
$t$ pdfs ![]() $\widehat {f_{\zeta _{t}}}(x)$ and the approximating pdfs
$\widehat {f_{\zeta _{t}}}(x)$ and the approximating pdfs ![]() $f_{\zeta _{K}}^{\textrm {TR}}(x)$. The areas between the pdfs must be in the interval
$f_{\zeta _{K}}^{\textrm {TR}}(x)$. The areas between the pdfs must be in the interval ![]() $(0,2)$ since the areas below each pdf is equal to
$(0,2)$ since the areas below each pdf is equal to ![]() $1$. The
$1$. The ![]() $L_{1}$ measure between the pdfs accounts for all
$L_{1}$ measure between the pdfs accounts for all ![]() $x\in ( 0,K_{\zeta })$,
$x\in ( 0,K_{\zeta })$, ![]() $\zeta = \gamma,\delta, \beta$. Denote this measure by
$\zeta = \gamma,\delta, \beta$. Denote this measure by
where
The measure ![]() $\rho (\widehat {f_{\zeta _{t}}}$,
$\rho (\widehat {f_{\zeta _{t}}}$, ![]() $f_{\zeta _{K}}^{\textrm {TR}})=0$ iff
$f_{\zeta _{K}}^{\textrm {TR}})=0$ iff ![]() $\widehat {f_{\zeta _{t}}}(x)=f_{\zeta _{K}}^{\textrm {TR}}(x)$ for all
$\widehat {f_{\zeta _{t}}}(x)=f_{\zeta _{K}}^{\textrm {TR}}(x)$ for all ![]() $x\in ( 0,K_{\zeta })$. Moreover,
$x\in ( 0,K_{\zeta })$. Moreover, ![]() $\rho (\widehat {f_{\zeta _{t}}},f_{\zeta _{K}}^{\textrm {TR}})\lt1$. The less the distance
$\rho (\widehat {f_{\zeta _{t}}},f_{\zeta _{K}}^{\textrm {TR}})\lt1$. The less the distance ![]() $\rho (\widehat {f_{\zeta _{t}}},f_{\zeta _{K}}^{\textrm {TR}})$, the better is the approximation (i.e.,
$\rho (\widehat {f_{\zeta _{t}}},f_{\zeta _{K}}^{\textrm {TR}})$, the better is the approximation (i.e., ![]() $\rho ( \widehat {f_{\zeta _{t}}},f_{\zeta _{K}}^{\textrm {TR}})$ is nearer to
$\rho ( \widehat {f_{\zeta _{t}}},f_{\zeta _{K}}^{\textrm {TR}})$ is nearer to ![]() $0$). The greater the distance
$0$). The greater the distance ![]() $\rho (\widehat {f_{\zeta _{t}}},f_{\zeta _{K}}^{\textrm {TR}})$, the worse is the approximation (i.e.,
$\rho (\widehat {f_{\zeta _{t}}},f_{\zeta _{K}}^{\textrm {TR}})$, the worse is the approximation (i.e., ![]() $\rho (\widehat {f_{\zeta _{t}}},f_{\zeta _{K}}^{\textrm {TR}})$ is nearer to
$\rho (\widehat {f_{\zeta _{t}}},f_{\zeta _{K}}^{\textrm {TR}})$ is nearer to ![]() $1$).
$1$).
(Other measures of discrepancy between pdfs are given on p. 35 and in Section 3.7 in [Reference Silverman19].)
5.2. Example values of the measure  ${\rho (\widehat {f_{\zeta _{t}}},f_{\zeta _{K}}^{\textrm {TR}})}$
${\rho (\widehat {f_{\zeta _{t}}},f_{\zeta _{K}}^{\textrm {TR}})}$
In the three examples here, the shape parameter of the Pareto(II) distribution is ![]() $\alpha =0.5$.
$\alpha =0.5$.
5.2.1. Excess when fixed time  $t=400$
$t=400$
For the example in Figure 8, we obtain ![]() $\rho (\widehat {f_{\gamma _{t}}},f_{\gamma _{K}}^{\textrm {TR}})= \mathbf {0.198468}$. The distance is uniformly quite close on the entire time interval (
$\rho (\widehat {f_{\gamma _{t}}},f_{\gamma _{K}}^{\textrm {TR}})= \mathbf {0.198468}$. The distance is uniformly quite close on the entire time interval (![]() $0,800$). The approximation of pdf
$0,800$). The approximation of pdf ![]() $\widehat {f_{\gamma _{t}}}$ by using pdf
$\widehat {f_{\gamma _{t}}}$ by using pdf ![]() $\rho (\widehat {f_{\gamma _{t}}} ,f_{\gamma _{K}}^{\textrm {TR}})$ is good.
$\rho (\widehat {f_{\gamma _{t}}} ,f_{\gamma _{K}}^{\textrm {TR}})$ is good.
5.2.2. Age when fixed time  $t=400$
$t=400$
For the example in Figure 9, we obtain ![]() $\rho (\widehat {f_{\delta _{t}}},f_{\delta _{K}}^{\textrm {TR}})= \mathbf {0.475558}$. The distance between the two pdfs is quite close on
$\rho (\widehat {f_{\delta _{t}}},f_{\delta _{K}}^{\textrm {TR}})= \mathbf {0.475558}$. The distance between the two pdfs is quite close on ![]() $( 0,200)$. It is not uniformly close on (0,400); starting at approximately time
$( 0,200)$. It is not uniformly close on (0,400); starting at approximately time ![]() $200$, the discrepancy increases rapidly on the interval
$200$, the discrepancy increases rapidly on the interval ![]() $(200,400)$. In addition, there is an atom with probability 0
$(200,400)$. In addition, there is an atom with probability 0![]() $.049938$ at time
$.049938$ at time ![]() $t$. The approximation of pdf
$t$. The approximation of pdf ![]() $\widehat { f_{\delta _{t}}}$ using
$\widehat { f_{\delta _{t}}}$ using ![]() $\rho (\widehat {f_{\delta _{t}}},f_{\delta _{K}}^{\textrm {TR}})$ is medium. Generally,
$\rho (\widehat {f_{\delta _{t}}},f_{\delta _{K}}^{\textrm {TR}})$ is medium. Generally, ![]() $\rho (\widehat {f_{\delta _{t}}} ,f_{\delta _{K}}^{\textrm {TR}})$ gives the analyst an idea of where the pdf
$\rho (\widehat {f_{\delta _{t}}} ,f_{\delta _{K}}^{\textrm {TR}})$ gives the analyst an idea of where the pdf ![]() $\widehat { f_{\delta _{t}}}(x)$ is located relative to
$\widehat { f_{\delta _{t}}}(x)$ is located relative to ![]() $f_{\delta _{K}}^{\textrm {TR}}(x)$.
$f_{\delta _{K}}^{\textrm {TR}}(x)$.
5.2.3. Total life when fixed time  $t=400$
$t=400$
For the example in Figure 10, we obtain ![]() $\rho (\widehat {f_{\beta _{t}}},f_{\beta _{K}}^{\textrm {TR}})= \mathbf {0.281637}$. The distance between the two pdfs is close on intervals
$\rho (\widehat {f_{\beta _{t}}},f_{\beta _{K}}^{\textrm {TR}})= \mathbf {0.281637}$. The distance between the two pdfs is close on intervals ![]() $( 0,150)$ and on
$( 0,150)$ and on ![]() $( 650,800)$. The overall distance is not uniformly close. The approximation of pdf
$( 650,800)$. The overall distance is not uniformly close. The approximation of pdf ![]() $\widehat {f_{\beta _{t}}}$ using
$\widehat {f_{\beta _{t}}}$ using ![]() $\rho (\widehat { f_{\beta _{t}}},f_{\beta _{K}}^{\textrm {TR}})$ is between good and medium. There is a rise in discrepancy starting at approximately time
$\rho (\widehat { f_{\beta _{t}}},f_{\beta _{K}}^{\textrm {TR}})$ is between good and medium. There is a rise in discrepancy starting at approximately time ![]() $150$ and increasing rapidly on
$150$ and increasing rapidly on ![]() $( 150,400)$. This rise appears similar to the discrepancy pattern in Figure 9 on interval
$( 150,400)$. This rise appears similar to the discrepancy pattern in Figure 9 on interval ![]() $( 200,400),$ for approximating
$( 200,400),$ for approximating ![]() $\widehat {f_{\delta _{t}}}(x)$. The variate of “total life” is equal to “age
$\widehat {f_{\delta _{t}}}(x)$. The variate of “total life” is equal to “age ![]() $+$ excess” (see Figure 1). In Figure 10, on interval
$+$ excess” (see Figure 1). In Figure 10, on interval ![]() $( 400,800)$, the distance decreases steadily, resembling Figure 8 for
$( 400,800)$, the distance decreases steadily, resembling Figure 8 for ![]() $\rho (\widehat {f_{\gamma _{t}}},f_{\gamma _{K}}^{\textrm {TR}})$. The discrepancy patterns for all three fixed finite time
$\rho (\widehat {f_{\gamma _{t}}},f_{\gamma _{K}}^{\textrm {TR}})$. The discrepancy patterns for all three fixed finite time ![]() $t$ pdfs appear to be related.
$t$ pdfs appear to be related.
6. Conclusion
(1) This article proposes a technique for approximating the analytic fixed finite time
 $t$ pdfs for large
$t$ pdfs for large  $t$, of excess, age, and total life, in a renewal process where the inter-renewals have a no-mean heavy-tailed distribution (extreme renewal process).
$t$, of excess, age, and total life, in a renewal process where the inter-renewals have a no-mean heavy-tailed distribution (extreme renewal process).(2) For the inter-renewals, we use the Pareto(II) variate (e.g., [Reference Arnold2]) with shape parameter
 $\alpha \in ( 0,1]$, as a generic example throughout the article, because of its common occurrence in recent research and applications.
$\alpha \in ( 0,1]$, as a generic example throughout the article, because of its common occurrence in recent research and applications.(3) Obtaining the analytic fixed finite time
 $t$ pdfs (
$t$ pdfs ( $t$ large) of excess age, and total life requires time-consuming computations. The greater
$t$ large) of excess age, and total life requires time-consuming computations. The greater  $t$ is, the more time-consuming is the computation. The approximating pdfs are the limiting pdfs of the fixed finite time
$t$ is, the more time-consuming is the computation. The approximating pdfs are the limiting pdfs of the fixed finite time  $t$ variates as
$t$ variates as  $t\rightarrow \infty$ in a companion renewal process, denoted by
$t\rightarrow \infty$ in a companion renewal process, denoted by  $\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$, where the inter-renewals are right-truncated Pareto(II) variates with finite mean, finite right truncation point
$\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$, where the inter-renewals are right-truncated Pareto(II) variates with finite mean, finite right truncation point  $K\gt0$ and the same shape parameter
$K\gt0$ and the same shape parameter  $\alpha \in ( 0,1]$. The limiting pdfs in
$\alpha \in ( 0,1]$. The limiting pdfs in  $\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$ exist because the inter-renewals have a finite mean, and have well-known formulas available from theory, not requiring any computation in the presented technique.
$\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$ exist because the inter-renewals have a finite mean, and have well-known formulas available from theory, not requiring any computation in the presented technique.(4) An
 $L_{1}$ distance measure between the analytic fixed finite time
$L_{1}$ distance measure between the analytic fixed finite time  $t$ pdfs of the excess, age, and total life (large
$t$ pdfs of the excess, age, and total life (large  $t$) in the extreme renewal process of interest
$t$) in the extreme renewal process of interest  $\{ Z_{n}\}_{n=1,2,\ldots }$, and the approximating limiting pdfs of excess, age, and total life in the companion renewal process
$\{ Z_{n}\}_{n=1,2,\ldots }$, and the approximating limiting pdfs of excess, age, and total life in the companion renewal process  $\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$ is considered in Section 5.
$\{Z_{K\!,n}^{\textrm {TR}}\}_{{n=1,2,\ldots }}$ is considered in Section 5.
Acknowledgments
The authors thank the reviewers for insightful comments which helped to improve the paper.
Funding statement
This research is supported by the Natural Sciences and Engineering Research Council of Canada [PHB-RGPIN-2014-05697; MLH-DDG-2019-04206].