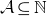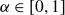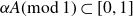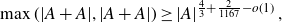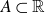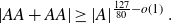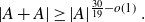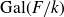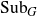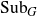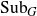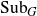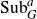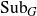Research Article
Chief factors in Polish groups
- Part of:
-
- Published online by Cambridge University Press:
- 30 June 2021, pp. 239-296
-
- Article
- Export citation
Trees of tangles in infinite separation systems
- Part of:
-
- Published online by Cambridge University Press:
- 22 July 2021, pp. 297-327
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Compact groups with a set of positive Haar measure satisfying a nilpotent law
- Part of:
-
- Published online by Cambridge University Press:
- 19 July 2021, pp. 329-332
-
- Article
- Export citation
A positive proportion of locally soluble quartic Thue equations are globally insoluble
- Part of:
-
- Published online by Cambridge University Press:
- 05 August 2021, pp. 333-348
-
- Article
- Export citation
Algebraic cycles and intersections of three quadrics
- Part of:
-
- Published online by Cambridge University Press:
- 07 September 2021, pp. 349-367
-
- Article
- Export citation
Remarks about inhomogeneous pair correlations
- Part of:
-
- Published online by Cambridge University Press:
- 06 September 2021, pp. 369-386
-
- Article
- Export citation
Fourier duality in the Brascamp–Lieb inequality
- Part of:
-
- Published online by Cambridge University Press:
- 27 September 2021, pp. 387-409
-
- Article
- Export citation
An update on the sum-product problem
- Part of:
-
- Published online by Cambridge University Press:
- 11 October 2021, pp. 411-430
-
- Article
- Export citation
Congruences for critical values of higher derivatives of twisted Hasse–Weil L-functions, III
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2021, pp. 431-456
-
- Article
- Export citation
Distal Actions of Automorphisms of Lie Groups G on SubG
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2021, pp. 457-478
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 173 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 August 2022, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
PSP volume 173 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 August 2022, pp. b1-b2
-
- Article
-
- You have access
- Export citation