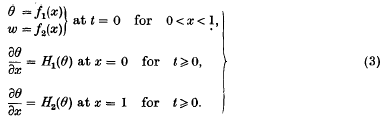Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 2969
A generalized inverse for matrices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 406-413
-
- Article
-
- You have access
- Export citation
- Cited by 2659
Note on Exchange Phenomena in the Thomas Atom
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 376-385
-
- Article
-
- You have access
- Export citation
- Cited by 2297
Quantum mechanics as a statistical theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 99-124
-
- Article
- Export citation
- Cited by 2086
Limiting forms of the frequency distribution of the largest or smallest member of a sample
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 180-190
-
- Article
- Export citation
- Cited by 2084
Discussion of Probability Relations between Separated Systems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 555-563
-
- Article
- Export citation
- Cited by 2063
A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 50-67
-
- Article
- Export citation
- Cited by 1976
The conductivity of thin metallic films according to the electron theory of metals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 100-108
-
- Article
- Export citation
- Cited by 1938
Theory of Statistical Estimation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 700-725
-
- Article
- Export citation
- Cited by 1853
The calculation of atomic fields
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 542-548
-
- Article
- Export citation
- Cited by 1637
Some generalized order-disorder transformations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 106-109
-
- Article
- Export citation
- Cited by 1539
Percolation processes: I. Crystals and mazes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 629-641
-
- Article
- Export citation
- Cited by 1230
The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Part I. Theory and Methods
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 89-110
-
- Article
- Export citation
- Cited by 1107
On the stability of crystal lattices. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 160-172
-
- Article
- Export citation
- Cited by 1007
Convection of a fluid in a porous medium
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 508-521
-
- Article
- Export citation
- Cited by 954
Spectral asymmetry and Riemannian Geometry. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 43-69
-
- Article
- Export citation
- Cited by 831
The flow due to a rotating disc
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 365-375
-
- Article
- Export citation
- Cited by 821
The stability of a queue with non-independent inter-arrival and service times
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 497-520
-
- Article
- Export citation
- Cited by 713
Random processes in genetics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 60-71
-
- Article
- Export citation
- Cited by 701
Probability relations between separated systems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 446-452
-
- Article
- Export citation
- Cited by 686
A Mathematical Theory of Natural and Artificial Selection, Part V: Selection and Mutation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 838-844
-
- Article
- Export citation