Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-26T01:13:14.822Z Has data issue: false hasContentIssue false
  • English
  • Français

Congruences for critical values of higher derivatives of twisted Hasse–Weil L-functions, III

Part of: Arithmetic algebraic geometry

Published online by Cambridge University Press:  19 October 2021

WERNER BLEY  and
DANIEL MACIAS CASTILLO
WERNER BLEY
Affiliation:
Ludwig–Maximilians-Universität München, Theresienstr. 39, D-80333 München, Germany. e-mail: bley@math.lmu.de
DANIEL MACIAS CASTILLO
Affiliation:
Departamento de Matemáticas, Universidad Autónoma de Madrid, 28049 Madrid, Spain and Instituto de Ciencias Matemáticas, 28049 Madrid, Spain. e-mail: daniel.macias@uam.es
Get access Rights & Permissions [Opens in a new window]

Abstract

Let A be an abelian variety defined over a number field k, let p be an odd prime number and let 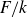$F/k$ be a cyclic extension of p-power degree. Under not-too-stringent hypotheses we give an interpretation of the p-component of the relevant case of the equivariant Tamagawa number conjecture in terms of integral congruence relations involving the evaluation on appropriate points of A of the ${\rm Gal}(F/k)$ -valued height pairing of Mazur and Tate. We then discuss the numerical computation of this pairing, and in particular obtain the first numerical verifications of this conjecture in situations in which the p-completion of the Mordell–Weil group of A over F is not a projective Galois module.

MSC classification

Primary: 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture
Secondary: 11G05: Elliptic curves over global fields 11G35: Varieties over global fields
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 173 , Issue 2 , September 2022 , pp. 431 - 456
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bertolini, M. and Darmon, H.. Derived heights and generalised Mazur–Tate regulators. Duke Math J. 76 No. 1 (1994), pp. 75–111.10.1215/S0012-7094-94-07604-7CrossRefGoogle Scholar
Bertolini, M. and Darmon, H.. Derived p-adic heights. Amer. J. Math. 117 (1995), pp. 1517-1554.Google Scholar
Bley, W.. Numerical evidence for the equivariant Birch and Swinnerton–Dyer conjecture. Exp. Math. 20 (2011), 426–456.10.1080/10586458.2011.565259CrossRefGoogle Scholar
Bley, W.. Numerical evidence for the equivariant Birch and Swinnerton–Dyer conjecture (part II). Math Comp. 81 (2012), 1681–1705.10.1090/S0025-5718-2012-02572-5CrossRefGoogle Scholar
Bley, W.. The equivariant Tamagawa number conjecture and modular symbols. Math. Ann. 356 (2013), 179–190.10.1007/s00208-012-0837-6CrossRefGoogle Scholar
Bley, W. and Macias Castillo, D.. Congruences for critical values of higher derivatives of twisted Hasse–Weil L-functions, J. Reine U. Angew . Math. 722 (2017), 105–136.Google Scholar
Burns, D. and Flach, M.. Tamagawa numbers for motives with (non-commutative) coefficients. Doc Math. 6 (2001), 501–570.Google Scholar
Burns, D., Kurihara, M. and Sano, T.. On zeta elements for $\mathbb{G}_m$ . Documenta Math. 21 (2016), 555–626.Google Scholar
Burns, D., Macias Castillo, D.. Organising matrices for arithmetic complexes. Int. Math. Res. Notices 2014 10 (2014), 2814-2883.Google Scholar
Burns, D. and Macias Castillo, D.. On refined conjectures of Birch and Swinnerton–Dyer type for Artin-Hasse–Weil L-series, submitted for publication.Google Scholar
Burns, D., Macias Castillo, D. and Wuthrich, C.. On Mordell–Weil groups and congruences between derivatives of twisted Hasse–Weil L-functions. J. Reine Angew Math.. 734 (2017), 187–228.Google Scholar
Burns, D. and Venjakob, O.. On descent theory and main conjectures in non-commutative Iwasawa theory. J. Inst. Math. Jussieu 10 (2011), 59-118.Google Scholar
Cremona, J.E., T.A.Fisher, C. O’Neil, D. Simon, M. Stoll. Explicit n-decent on elliptic curves, I. Algebra. J. Reine Angew. Math 615 (2008), 121–155.Google Scholar
Cremona, J.E., T.A.Fisher, C. O’Neil, D. Simon, M. Stoll. Explicit n-decent on elliptic curves, I. Geometry. J. Reine Angew. Math 632 (2009), 63–84.Google Scholar
Cremona, J.E., T.A.Fisher, C. O’Neil, D. Simon and M. Stoll. Explicit n-decent on elliptic curves. I. Algorithms, Mathematics of Computation 84, Vol.292, (2014), 895-922.10.1090/S0025-5718-2014-02858-5CrossRefGoogle Scholar
Coates, J., Fukaya, T., Kato, K., Sujatha, R. and Venjakob, O.. The ${\rm GL}_2$ -main conjecture for elliptic curves without complex multiplication. Publ. IHES 101 (2005), 163-208.Google Scholar
Darmon, H.. A refined conjecture of Mazur–Tate type for Heegner points. Invent. Math. 110 (1992), 123–146.10.1007/BF01231327CrossRefGoogle Scholar
Fisher, T. and Newton, R.. Computing the Cassels-Tate pairing on the 3-Selmer group of an elliptic curve. Int. J. Number Theory 10 (2014), no. 7, 1881-1907.Google Scholar
Geishauser, C.. Computation of 2-extensions of dual Selmer groups, Master thesis. LMU (2018).Google Scholar
Hilton, P. J. and Stammbach, U.. A course in Homological Algebra, (Springer-Verlag, New York, 1970).Google Scholar
Lawson, T. and Wuthrich, C.. Vanishing of some Galois cohomology groups for elliptic curves. in: Elliptic Curves, Modular Forms and Iwasawa Theory (ed. Loeffler, D. and Zerbes, S. L. ), Springer Proc. in Math. and Stat., 188 (2017), 373-399.Google Scholar
Macias Castillo, D.. Congruences for critical values of higher derivatives of twisted Hasse–Weil L-functions, II, Acta Arith. 195 (2020), no. 7, 327-365.Google Scholar
Mazur, B. and Tate, J.. Canonical height pairings via biextensions. In: ‘Arithmetic and Geometry’ vol. 1. Prog Math. 35 (1983), 195–237.Google Scholar
Mazur, B. and Tate, J.. Refined conjectures of the Birch and Swinnerton–Dyer type. Duke Math. J. 54 (1987), 711–750.10.1215/S0012-7094-87-05431-7CrossRefGoogle Scholar
Neukirch, J.. Algebraic Number Theory (Springer-Verlag, 1999).10.1007/978-3-662-03983-0CrossRefGoogle Scholar
Schaefer, E.F. and Stoll, M.. How to do a p-descent on an ellitpic curve. Tran. AMS, 356 (2003), 1209-1231.Google Scholar
Schaefer, E.F.. Computing a Selmer group of a Jacobian using functions on the curve. Math. Anna., 310 (1998), 447–471.10.1007/s002080050156CrossRefGoogle Scholar
Schaefer, E.F.. Computing a Selmer group of a Jacobian using functions on the curve, ArXiv e-prints, July 2015.Google Scholar
Tan, K.-S.. p-adic pairings. Contemp. Math. 165 (1994), 111–121.10.1090/conm/165/01616CrossRefGoogle Scholar
Visse, E.. Calculating the Tate local pairing for any odd prime number, ArXiv e-prints, October 2016.Google Scholar
Yakovlev, A. V.. Homological definability of p-adic representations of groups with cyclic Sylow p-subgroup. An. St. Univ. Ovidius Constanta 4 (1996), 206-221.Google Scholar