Hostname: page-component-848d4c4894-mwx4w Total loading time: 0 Render date: 2024-06-25T01:23:36.710Z Has data issue: false hasContentIssue false
  • English
  • Français

A positive proportion of locally soluble quartic Thue equations are globally insoluble

Part of: Diophantine equations

Published online by Cambridge University Press:  05 August 2021

SHABNAM AKHTARI
SHABNAM AKHTARI*
Affiliation:
Fenton Hall, University of Oregon, Eugene, OR 97403-1222 U.S.A e-mail: akhtari@uoregon.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

For any fixed nonzero integer h, we show that a positive proportion of integral binary quartic forms F do locally everywhere represent h, but do not globally represent h. We order classes of integral binary quartic forms by the two generators of their ring of 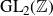${\rm GL}_{2}({\mathbb Z})$ -invariants, classically denoted by I and J.

MSC classification

Primary: 11D25: Cubic and quartic equations 11D45: Counting solutions of Diophantine equations
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 173 , Issue 2 , September 2022 , pp. 333 - 348
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akhtari, S.. Representation of small integers by binary forms. Q. J. Math 66 (4) (2015), 1009–1054.10.1093/qmath/hav026CrossRefGoogle Scholar
Akhtari, S. and Bhargava, M.. A positive proportion of Thue equations fail the integral Hasse principle. Amer. J. of Math. 141, no. 2 (2019), 283–307.10.1353/ajm.2019.0006CrossRefGoogle Scholar
Bhargava, M. and Gross, B.. The average size of the 2-Selmer group of Jacobians of hyperelliptic curves having a rational Weierstrass point. Automorphic representations and L-functions, 23-91, Tata Inst. Fundam. Res. Stud. Math., 22 (Tata Inst. Fund. Res., Mumbai, 2013).Google Scholar
Bhargava, M. and Shankar, A.. Binary quartic forms having bounded invariants, and the boundedness of the average rank of elliptic curves. Ann. of Math. (2) 181 (2015), no. 1, 191–242.Google Scholar
Birch, B. J. and Merriman, J. R.. Finiteness theorems for binary forms with given discriminant. Proc. London Math. Soc. 25 (1972), 385–394.Google Scholar
Bombieri, E. and Schmidt, W. M.. On Thue’s equation . Invent. Math. 88 (1987), 69–81.10.1007/BF01405092CrossRefGoogle Scholar
Davenport, H. and Heilbronn, H.. On the density of discriminants of cubic fields II. Proc. Roy. Soc. London Ser. A 322 (1971), no. 1551, 405–420.Google Scholar
Evertse, J. H. and GyÖry, K.. Effective finiteness results for binary forms with given discriminant . Compositio Math, 79 (1991), 169–204.Google Scholar
Leep, D. B. and Yeomans, C. C.. The number of points on a singular curve over a finite field . Arch. Math. 63 (1994), 420–426.10.1007/BF01196671CrossRefGoogle Scholar
Stewart, C. L.. On the number of solutions of polynomial congruences and Thue equations. J. Amer. Math . Soc. 4 (1991), 793–838.Google Scholar