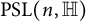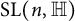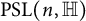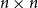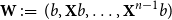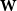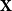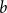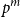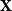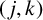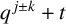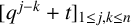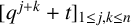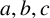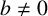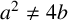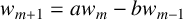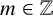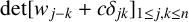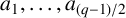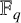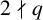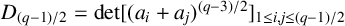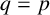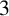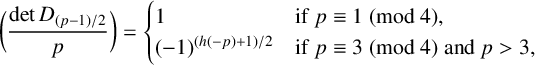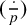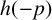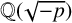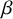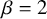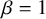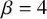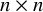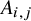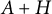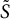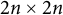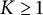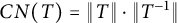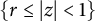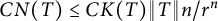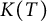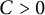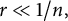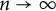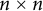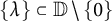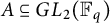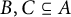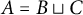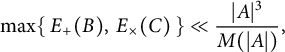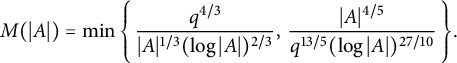60 results in 15Bxx
Moments of the free Jacobi process: A matrix approach
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 10 March 2025, pp. 1-26
-
- Article
- Export citation
Spectral identities for Schrödinger operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 13 January 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Product of two involutions in quaternionic special linear group
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 08 January 2025, pp. 1-19
-
- Article
- Export citation
Full Poissonian local statistics of slowly growing sequences
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 148-180
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Completion problems and sparsity for Kemeny’s constant
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 20 November 2024, pp. 1-18
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cokernel statistics for walk matrices of directed and weighted random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 18 October 2024, pp. 131-150
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The full rank condition for sparse random matrices
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 20 September 2024, pp. 643-707
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CHARACTERISTIC POLYNOMIALS OF THE MATRICES WITH
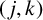 $(\,j,k)$-ENTRY
$(\,j,k)$-ENTRY 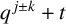 $q^{\,j\pm k}+t$
$q^{\,j\pm k}+t$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 03 June 2024, pp. 228-237
- Print publication:
- April 2025
-
- Article
-
- You have access
- HTML
- Export citation
Counting elements of the congruence subgroup
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 22 May 2024, pp. 955-969
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
ON GENERALISED LEGENDRE MATRICES INVOLVING ROOTS OF UNITY OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 199-210
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
Asymptotic expansion of
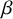 $\beta $ matrix models in the multi-cut regime
$\beta $ matrix models in the multi-cut regime
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 24 January 2024, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The least singular value of a random symmetric matrix
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 23 January 2024, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reversibility of affine transformations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 08 November 2023, pp. 1217-1228
-
- Article
- Export citation
Autocorrelations of characteristic polynomials for the Alternative Circular Unitary Ensemble
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 51-64
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Representatives of similarity classes of matrices over PIDs corresponding to ideal classes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 18 October 2023, pp. 88-103
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Block perturbation of symplectic matrices in Williamson’s theorem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 201-214
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Phase transition for the generalized two-community stochastic block model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 31 July 2023, pp. 385-400
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
On the condition number of a Kreiss matrix
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1376-1390
- Print publication:
- December 2023
-
- Article
- Export citation
An energy decomposition theorem for matrices and related questions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1280-1295
- Print publication:
- December 2023
-
- Article
- Export citation
Linear optimization over homogeneous matrix cones
- Part of
-
- Journal:
- Acta Numerica / Volume 32 / May 2023
- Published online by Cambridge University Press:
- 11 May 2023, pp. 675-747
-
- Article
-
- You have access
- Open access
- Export citation