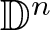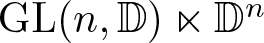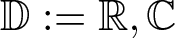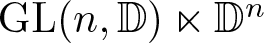1. Introduction
Let G be a group. An element 
$g \in G$ is called reversible or real if g is conjugate to g −1 in G. An element 
$g \in G$ is strongly reversible or strongly real if g is conjugate to g −1 in G by an involution (i.e., by an element of order at most 2) in G. Equivalently, an element is strongly reversible if it is a product of two involutions from G; see Remark 4.3. The idea of ‘reversible elements’ originated in mathematical and physical systems from different directions, cf. [Reference Arnol’d, Avez, Avez and Benjamin1, Reference Devaney3, Reference Lamb10, Reference O’Farrell and Short11, Reference Sevryuk13]. From the algebraic point of view, the terms real and strongly real are used instead of reversible and strongly reversible. Investigation of reversible and strongly reversible elements in a group is an active area of current research; see [Reference O’Farrell and Short11] for an elaborate exposition of this theme from the geometric point of view. A complete classification of reversible and strongly reversible elements is not available in the literature except for the case of a few families of infinite groups, which include the compact Lie groups, real rank one classical groups and isometry groups of hermitian spaces; see [Reference Bhunia and Gongopadhyay2, Reference Gongopadhyay and Lohan5, Reference O’Farrell and Short11]. In this article, by reversibility in a group G, we mean a classification of reversible and strongly reversible elements in G.
Let 
$\mathbb D :=\mathbb R,\mathbb C$ or 
$ \mathbb H$. The space 
$ \mathbb D^n $ equipped with a (right) 
$\mathbb D$-Hermitian form gives a model for Hermitian geometry. When 
$ \mathbb D=\mathbb R $, this is the well-known classical Euclidean geometry. The reversibility problem in the isometry group 
$ {\rm O}(n) \ltimes \mathbb R^n $ of the n-dimensional Euclidean space was classified by Short in [Reference Short14]. This has been extended in [Reference Gongopadhyay and Lohan5] for the isometry group 
$ {\rm U}(n,\mathbb F) \ltimes \mathbb F^n $ of the 
$\mathbb F$-Hermitian space, where 
$\mathbb F:= \mathbb C $ or 
$\mathbb H$.
Considering 
$\mathbb D^n $ as an affine space, the group of automorphisms of 
$\mathbb D^n$, denoted by 
$ \mathrm{Aff}(n,\mathbb D) $, is given by 
$\mathrm{GL}(n,\mathbb D) \ltimes \mathbb D^n $. The affine space is important to understand the affine structure on geometric manifolds; see the tome [Reference Goldman4] for details. Understanding reversible and strongly reversible elements in the affine group 
$ \mathrm{Aff}(n,\mathbb D) $ is a natural problem of interest. In this paper, we have investigated this problem. Our main result is as follows:
Theorem 1.1. Let 
$g = (A,v) \in \mathrm{Aff}(n,\mathbb D) $ be an arbitrary element, where 
$ \mathbb D = \mathbb R, \mathbb C$ or 
$\mathbb H$. Then g is reversible (respectively, strongly reversible) in 
$\mathrm{Aff}(n,\mathbb D) $ if and only if A is reversible (respectively, strongly reversible) in 
$\mathrm{GL}(n,\mathbb D)$. Further, for 
$\mathbb D = \mathbb R $ or 
$\mathbb C$, the following statements are equivalent.
(1) g is reversible in
$\mathrm{Aff}(n,\mathbb D) $.(2) g is strongly reversible in
$\mathrm{Aff}(n,\mathbb D) $.
This theorem answers a problem raised in [Reference O’Farrell and Short11, p. 78–79]. Note that the classification of the reversible and strongly reversible elements in 
$ \mathrm{Aff}(n,\mathbb D) $ is intimately related to the corresponding classification in 
$\mathrm{GL}(n,\mathbb D)$. Such classification in 
$\mathrm{Aff}(n,\mathbb D)$ can be obtained by combining Theorem 1.1 with the reversibility in 
$\mathrm{GL}(n,\mathbb D)$. The reversibility in 
${\rm GL}(n, \mathbb D)$ is well known for 
$\mathbb D=\mathbb R$ or 
$\mathbb C$, cf. [Reference O’Farrell and Short11, Reference Wonenburger15], and this has been extended over the quaternions recently, cf. [Reference Gongopadhyay, Lohan, Maity and Papadopoulos6].
To prove the above theorem, first, we investigate conjugacy in 
${\rm Aff}(n,\mathbb D)$ in Lemma 3.4. Then using Lemma 3.4, reversibility in 
${\rm Aff}(n,\mathbb D)$ boils down to the case when the linear part of the affine transformation is unipotent. We consider the Lie algebra 
$\mathfrak{aff}(n, \mathbb D)$ of the affine group 
${\rm Aff}(n,\mathbb D)$ and consider the adjoint action; see Equation (3.4). Then we apply the notion of ‘adjoint reality’ introduced in [Reference Gongopadhyay and Maity7], also see Section 3.3, to classify the strongly reversible elements in 
${\rm Aff}(n,\mathbb D)$ whose linear parts are unipotent; see Proposition 3.11.
The reversibility problem is closely related to the problem of finding the involution length of a group. The involution length of a group G is the least integer m so that any element of G can be expressed as a product of m involutions in G; see [Reference O’Farrell and Short11, p. 76]. Now we state our second result. We refer to Definition 4.1 for the notion of quaternionic determinant.
Theorem 1.2. Let 
$ g = (A,v) \in {\rm Aff}(n,\mathbb D) $ such that 
$ \mathrm{det}(A) \in \{-1,1\}$. Then g can be written as a product of at most four involutions for 
$ \mathbb D=\mathbb R, \mathbb C $ or 
$\mathbb H$.
1.1. Structure of the paper
The structure of the paper is as follows. In Section 2, we fix some notation and recall some necessary background. In Section 3, we consider the affine group and prove the main result of this article, Theorem 1.1. Finally, in Section 4, we investigate the product of involutions in the affine group 
$ {\rm Aff}(n,\mathbb D)$ and prove Theorem 1.2.
2. Preliminaries
Let 
$\mathbb H:=\mathbb R\, +\,\mathbb R\mathbf{i} +\,\mathbb R\mathbf{j}+\,\mathbb R\mathbf{k}$ be the division algebra of Hamilton’s quaternions. We will use the notation 
$\mathbb D$ to denote either 
$\mathbb R, \mathbb C$ or 
$ \mathbb H$ unless otherwise specified. We consider 
$ \mathbb D^n$ as a right 
$\mathbb D$-module. We begin by recalling some basic notions of quaternion linear algebra. We refer the reader to [Reference Rodman12, Chapter 3, Chapter 5] for a detailed exposition of the theory of linear transformations over the quaternions.
Definition 2.1. (cf. [Reference Rodman12, p. 90])
Let 
$ \mathrm{M}(n,\mathbb H)$ be the algebra of n × n matrices over 
$\mathbb H$. A non-zero vector 
$v \in \mathbb H^n $ is said to be a (right) eigenvector of 
$A \in \mathrm{M}(n,\mathbb H)$ corresponding to a (right) eigenvalue 
$\lambda \in \mathbb H $ if the equality 
$ A v = v\lambda $ holds.
Note that eigenvalues of 
$A\in \mathrm{M}(n,\mathbb H)$ occur in similarity classes, and each similarity class of eigenvalues contains a unique complex representative with non-negative imaginary part. Here, instead of similarity classes of eigenvalues, we will consider the unique complex representative with non-negative imaginary part.
Definition 2.2. (cf. [Reference Rodman12, p. 94])
A Jordan block 
$\mathrm{J}(\lambda,m)$ is an m × m matrix with 
$ \lambda \in \mathbb D$ on the diagonal entries, 1 on all of the super-diagonal entries and zero elsewhere. We will refer to a block diagonal matrix where each block is a Jordan block as Jordan form.
Jordan canonical forms in 
$\mathrm{GL}(n,\mathbb D)$ are well studied in the literature; see [Reference Rodman12, Chapter 5, Chapter 15]. Recall that an element 
$U \in \mathrm{GL}(n,\mathbb D)$ is called unipotent if each eigenvalue of U equals to 1. In our convention, we shall include identity as the only unipotent element, which is also semisimple. The next result provides the Jordan form for a given unipotent element in 
$ \mathrm{GL}(n,\mathbb D)
$.
Lemma 2.3. (cf. [Reference Rodman12, Theorem 15.1.1, Theorem 5.5.3])
For every unipotent element 
$A \in \mathrm{GL}(n,\mathbb D)$, there is an invertible matrix 
$S \in \mathrm{GL}(n,\mathbb D)$ such that SAS −1 has the following form:
\begin{equation} SAS^{-1} =\mathrm{I}_{m_0} \oplus \mathrm{J}(1, m_1) \oplus \cdots \oplus \mathrm{J}(1, \, m_k),
\end{equation} where 
$ m_i \in \mathbb N,$ for all 
$ i \in \{0, 1,2, \dots, k\}.$ The form (2.1) is uniquely determined by A up to a permutation of diagonal blocks.
Now we recall a well-known result, which gives equivalence between reversible and strongly reversible elements in 
${\rm GL }(n,\mathbb D) $ for 
$\mathbb{D} = \mathbb R$ or 
$ \mathbb C$.
Proposition 2.4. (cf. [Reference O’Farrell and Short11, Theorems 4.7])
Let 
$A \in {\rm GL }(n,\mathbb D) $, where 
$\mathbb{D} = \mathbb R$ or 
$ \mathbb C$. Then A is reversible in 
$ {\rm GL }(n,\mathbb D) $ if and only if A is strongly reversible in 
$ {\rm GL }(n,\mathbb D) $.
We would like to mention that the above equivalence does not hold for the case 
$\mathbb D =\mathbb H$, e.g., 
$A = (\mathbf{i}) \in {\rm GL }(1,\mathbb H)$ is reversible but not strongly reversible in 
${\rm GL }(1,\mathbb H)$.
3. Reversibility in the affine group $\mathrm{Aff}(n,\mathbb D)$
Consider the affine space 
$\mathbb D^n$, where 
$\mathbb D =\mathbb R,\mathbb C $ or 
$\mathbb H$. Let 
$ \mathrm{Aff}(n,\mathbb D)$ denote the affine group of all invertible affine transformations from 
$\mathbb D^n$ to 
$\mathbb D^n$. Each element 
$g = (A,v)$ of 
$\mathrm{GL}(n,\mathbb D) \ltimes \mathbb D^n $ acts on 
$\mathbb D^n$ as affine transformation
\begin{equation*}g(x) = A(x) + v,\end{equation*} where 
$A \in {\mathrm{GL}}(n,\mathbb D) $ is called the linear part of g and 
$v \in \mathbb D^n$ is called the translation part of g. This action identifies the affine group 
$\mathrm{Aff}(n,\mathbb D)$ with 
$ \mathrm{GL}(n,\mathbb D) \ltimes \mathbb D^n $. We can embed 
$\mathbb D^n$ into 
$\mathbb D^{n+1}$ as the plane 
$ \mathbf{P} := \{(x,1) \in \mathbb D^{n+1} \mid x \in \mathbb D^n \}$. Consider the embedding 
$\Theta : \mathrm{Aff}(n,\mathbb D) \longrightarrow \mathrm{GL}(n+1,\mathbb D)$ defined as
\begin{equation}
\Theta ( (A,v)) = \begin{pmatrix} A & v \\
\mathbf{0} & 1 \\
\end{pmatrix},
\end{equation} where 0 is the zero vector in 
$\mathbb D^n$. Note that action of 
$ \Theta ( \mathrm{Aff}(n,\mathbb D))$ on the plane P is exactly the same as the action of 
$\mathrm{Aff}(n,\mathbb D)$ on 
$\mathbb D^n $. In this section, we will classify reversible and strongly reversible elements in the affine group 
$\mathrm{Aff}(n,\mathbb D)$. We begin with an example.
Example 3.1. Let 
$g= (\mathrm{I}_n, v) \in \mathrm{Aff}(n,\mathbb D) $. Consider 
$g_1= (-\mathrm{I}_n, \mathbf{0}) $ and 
$g_2= (-\mathrm{I}_n, -v)$ in 
$\mathrm{Aff}(n,\mathbb D)$. Then g 1 and g 2 are involutions in 
$\mathrm{Aff}(n,\mathbb D) $ such that
\begin{equation*} g= g_1 \, g_2,\ \hbox{i.e., }\ (\mathrm{I}_n, v) = (-\mathrm{I}_n, \mathbf{0}) \, (-\mathrm{I}_n, -v).\end{equation*} Hence, g is strongly reversible in 
$\mathrm{Aff}(n,\mathbb D) $.
In the next result, we obtain necessary and sufficient conditions for the reversible elements in 
$ \mathrm{Aff}(n,\mathbb D) $.
Lemma 3.2. Let 
$g = (A,v) \in \mathrm{Aff}(n,\mathbb D) $ be an arbitrary element. Then g is reversible in 
$\mathrm{Aff}(n,\mathbb D) $ if and only if there exists an element 
$h = (B,w) \in \mathrm{Aff}(n,\mathbb D) $ such that both the following conditions hold:
(1)
$BAB^{-1} = A^{-1}$,(2)
$(A^{-1} - \mathrm{I}_n)(w) = (A^{-1} + B)(v)$.
Proof. Note that 
$g^{-1}(x) = A^{-1}(x) - A^{-1}(v)\ \hbox {and } h^{-1}(x) = B^{-1}(x) - B^{-1}(w)$ for all 
$x \in \mathbb D^n$. This implies for all 
$x \in \mathbb D^n$, we have
\begin{equation*}
hgh^{-1}(x) = h (AB^{-1}(x) - AB^{-1}(w)+v) = BAB^{-1}(x) - BAB^{-1} (w) +B(v) + w.
\end{equation*} Therefore, 
$hgh^{-1} = g^{-1} \Leftrightarrow BAB^{-1} = A^{-1} \ \hbox {and } - A^{-1}(v) = - BAB^{-1} (w) +B(v) + w$. This proves the lemma.
The following lemma gives necessary and sufficient conditions for the strongly reversible elements in 
$ \mathrm{Aff}(n,\mathbb D) $.
Lemma 3.3. Let 
$g = (A,v) \in \mathrm{Aff}(n,\mathbb D) $ be an arbitrary element. Then g is strongly reversible in 
$\mathrm{Aff}(n,\mathbb D) $ if and only if there exists an element 
$h = (B,w) \in \mathrm{Aff}(n,\mathbb D) $ such that both the following conditions hold:
(1)
$BAB^{-1} = A^{-1}$ and $ B^2 = \mathrm{I}_n$,(2)
$(B+\mathrm{I}_n)(w)=\mathbf{0}$ and $(B+A^{-1})(w-v)=\mathbf{0}$.
Proof. Note that 
$h = (B,w) \in \mathrm{Aff}(n,\mathbb D) $ is an involution if and only if 
$h^2(x) = B^2(x)+ B(w) + w = x \ {\textrm {for}}\ {\textrm{all}}\ x \in \mathbb D^n$. This implies that 
$ B^2 = \mathrm{I}_n$ and 
$(B + \mathrm{I}_n)(w)=0$. Further, in view of Lemma 3.2, 
$hgh^{-1}= g^{-1} $ if and only if conditions (1) and (2) of Lemma 3.2 hold. Observe that equation 
$(B + \mathrm{I}_n)(w)=0$ and equation 
$(A^{-1} - \mathrm{I}_n)(w) = (A^{-1} + B)(v)$ implies 
$(B+A^{-1})(w-v)=\mathbf{0}$. This proves the lemma.
3.1. Conjugacy in the affine group $\mathrm{Aff}(n,\mathbb D)$
In the affine group 
$\mathrm{Aff}(n,\mathbb D)$, up to conjugacy, we can consider every element in a more simpler form, which is demonstrated in the next lemma. Recall that a unipotent element 
$U \in \mathrm{GL}(n,\mathbb D)$ has only 1 as an eigenvalue.
Lemma 3.4. Every element g in 
$ \mathrm{Aff}(n,\mathbb D)$, up to conjugacy, can be written as 
$g = (A, v)$ such that 
$A = T \oplus U$, where 
$T \in \mathrm{GL}(n-m,\mathbb D)$, 
$U \in \mathrm{GL}(m,\mathbb D)$ such that T does not have eigenvalue 1, U has only 1 as eigenvalue and v is of the form 
$v = [0,0,\dots,0,v_1,v_2,\dots,v_m] \in \mathbb D^n$, where 
$0\leq m \leq n$ is the multiplicity of eigenvalue 1 of the linear part of g. Further, if 1 is not an eigenvalue of the linear part of g (i.e., m = 0), then up to conjugacy, g is of the form 
$g = (A, \mathbf{0} )$.
Proof. Let 
$g \in \mathrm{Aff}(n,\mathbb D) $ be an arbitrary element. In view of the Jordan decomposition in 
$\mathrm{GL}(n,\mathbb D)$, after conjugating g by a suitable element 
$(B,\mathbf{0}) \in \mathrm{Aff}(n,\mathbb D)$, we can assume 
$g = (A,w)$ such that 
$A = T \oplus U$, where 
$T \in \mathrm{GL}(n-m,\mathbb D)$ does not have eigenvalue 1 and 
$U \in \mathrm{GL}(m,\mathbb D)$ is unipotent. There are two possible cases:
(1) Suppose 1 is not an eigenvalue of A. So the linear transformation
$A - \mathrm{I}_n$ is invertible. Therefore, we can choose $x_o =(A - \mathrm{I}_n )^{-1} (w) \in \mathbb D^n$. Consider $h = (\mathrm{I}_n, x_o) \in \mathrm{Aff}(n,\mathbb D)$. For all $x \in \mathbb D^n$, we have
\begin{equation*} hgh^{-1} (x) = hg(x- x_o) = h({A}x - {A}x_o + w ) ={A}x + w - ({A}-{\rm I}_n)x_o.\end{equation*}This implies
$hgh^{-1} (x)= {A}(x) + \mathbf{0} $ for all $x \in \mathbb D^n$, since $x_o =({A} - {{\rm I}_n} )^{-1} (w)$.(2) Let 1 be an eigenvalue of A. In this case m > 0 and
${A} - {{\rm I}_n}$ has rank $ n-m \lt n$. So we can choose an element $u \in \mathbb D^n$ having the last m coordinates zero such that $ [({A} - {{\rm I}_n} )(u)]_i = w_i\ \hbox{for all } \ 1 \leq i \leq n-m,\ \hbox{where } w = [w_i]_{1 \le i \le n}$. Let $v = w{- }({A} {-} {{\rm I}_n} )(u)$. Then $v = [0,0, \dots, 0,w_{n-m+1}, w_{n-m+2},\dots,w_n ] \in \mathbb D^n$. Now consider $h = ( \mathrm{I}_n,u) \in \mathrm{Aff}(n,\mathbb D)$. For all $x \in \mathbb D^n$, we have
\begin{equation*}hgh^{-1}(x) = hg(x-u) = h(Ax - Au +w) = Ax + w-(A - \mathrm{I}_n)(u) = Ax +v.\end{equation*}
This completes the proof.
Remark 3.5. The idea of the above proof is in the same line of arguments as in [Reference Gongopadhyay and Lohan5, Lemma 3.1]. But here, we have to deal with the subtle situation when the linear part of affine transformations contains a unipotent Jordan block.
3.2. Elements in $\mathrm{Aff}(n,\mathbb D)$ having a fixed point
Recall that if the linear part of an element in 
$\mathrm{Aff}(n,\mathbb D) $ does not have eigenvalue 1, then it will have a fixed point in 
$\mathbb D^n$. In this case, the classification of reversible and strongly reversible elements in 
$\mathrm{Aff}(n,\mathbb D) $ follows from the corresponding classification in 
$\mathrm{GL}(n,\mathbb D)$.
Proposition 3.6. Let 
$g = (A,v) \in \mathrm{Aff}(n,\mathbb D) $ be an arbitrary element such that 1 is not an eigenvalue of the linear part A of g. Then g is reversible (respectively strongly reversible) in 
$\mathrm{Aff}(n,\mathbb D) $ if and only if A is reversible (respectively, strongly reversible) in 
$\mathrm{GL}(n,\mathbb D)$. Further, for 
$\mathbb D = \mathbb R $ or 
$\mathbb C$, the following are equivalent.
(1) g is reversible in
$\mathrm{Aff}(n,\mathbb D) $.(2) g is strongly reversible in
$\mathrm{Aff}(n,\mathbb D) $.
3.3. Elements in $\mathrm{Aff}(n,\mathbb D)$ with unipotent linear part
In this section, we shall use the adjoint reality approach introduced in [Reference Gongopadhyay and Maity7] to show that every element of 
$\mathrm{Aff}(n,\mathbb D)$ with a unipotent linear part is strongly reversible. In view of Lemma 3.4 and Proposition 3.6, classification of reversible and strongly reversible elements in 
$\mathrm{Aff}(n,\mathbb D) $ reduces to the case when the linear part of the affine group element is unipotent.
In view of Lemma 2.3, every unipotent element in 
$\mathrm{GL}(n,\mathbb D)$ can be written as direct sum of unipotent Jordan blocks; see Equation (2.1). Therefore, it is enough to consider the case when the linear part of an element 
$g \in \mathrm{Aff}(n,\mathbb D) $ is equal to the unipotent Jordan block 
$\mathrm{J}(1,n)$. We will show that 
$ g =(\mathrm{J}(1, \, n),v) \in \mathrm{Aff}(n,\mathbb D) $ is strongly reversible in 
$\mathrm{Aff}(n,\mathbb D) $ for all 
$v \in \mathbb D^n$ and 
$n\in \mathbb N$. In the following example, we will illustrate this for the case n = 6 by constructing an explicit involution, which conjugate g to g −1.
Example 3.7. Let 
$g = (A,v) \in \mathrm{Aff}(6,\mathbb D) $ be such that 
$A = \mathrm{J}(1, 6) \in \mathrm{GL}(6,\mathbb D) $, where 
$ \mathbb D = \mathbb R, \mathbb C$ or 
$\mathbb H$. We will show that g is strongly reversible in 
$\mathrm{Aff}(6,\mathbb D) $.
\begin{equation} Here,\ A^{-1} = \begin{pmatrix}
1 & -1 &1 &-1&1 &-1 \\
& 1 & -1&1&-1&1 \\
& & 1&-1&1&-1 \\
& & &1&-1&1 \\
& & & & 1 &-1 \\
& & & & &1
\end{pmatrix} .\end{equation}
Let 
\begin{equation}B := \begin{pmatrix}
1 & 4 &6 &4&1 &0 \\
& -1 & -3&-3&-1&0 \\
& & 1&2&1&0 \\
& & &-1&-1&0 \\
& & & & 1 &0 \\
& & & & &-1
\end{pmatrix}\end{equation} be an element of 
${\rm GL }(6,\mathbb D)$. Note that B is an involution in 
${\rm GL }(6,\mathbb D)$ and it conjugates A to A −1. Further, we have
\begin{equation}
B+ \mathrm{I}_6 = \begin{pmatrix}
2 & 4 &6 &4&1 &0 \\
& 0 & -3&-3&-1&0 \\
& & 2&2&1&0 \\
& & &0&-1&0 \\
& & & & 2 &0 \\
& & & & &0
\end{pmatrix}, \qquad B +A^{-1} = \begin{pmatrix}
2 & 3 &7 &3&2 &-1 \\
& 0 & -4&-2&-2&1 \\
& & 2&1&2&-1 \\
& & &0&-2&1 \\
& & & &2 &-1 \\
& & & & &0
\end{pmatrix}.
\end{equation} Note that both the matrices 
$B + \mathrm{I}_6$ and 
$B + A^{-1}$ have the same rank, which is equal to 3. Moreover, their corresponding diagonal entries are equal. Now, consider 
$h = (B,w) \in \mathrm{Aff}(6,\mathbb D) $, where 
$w \in \mathbb D^n$ is defined as
\begin{equation}
w = \begin{pmatrix}
4v_1+6v_2+10v_3+4v_2 \\
-2v_1-3v_2-7v_3-3v_4 \\
2v_3+v_4 \\
-2v_3-v_4 \\
0 \\
v_6-2v_5
\end{pmatrix}.
\end{equation} Then h satisfies all the conditions of Lemma 3.3. Therefore, h is an involution such that 
$hgh^{-1} =g^{-1}$. Hence, g is strongly reversible in 
$\mathrm{Aff}(6,\mathbb D) $.
The complexity of computation involved in Example 3.7 increases as n (size of the Jordan block) increases if we follow the above approach. Therefore, when the linear part of 
$g \in \mathrm{Aff}(n,\mathbb D) $ is 
$\mathrm{J}(1, n)$, generalizing the above construction to find reversing involution for g seems to be difficult. We will choose a different path to avoid the computational difficulties and give a significantly simpler proof by considering adjoint reality in the Lie algebra set-up; see Lemma 3.10.
First, let us introduce some notation that will be used in the next part of this section. As before, let 
$ \mathbb D^n $ be the right 
$\mathbb D $-vector space. Consider 
$ \mathbb D^n $ as an abelian Lie algebra. Then 
$ {\rm Der}_{\mathbb{D}}\mathbb{D}^{n} \simeq \mathfrak{g}\mathfrak{l}(n,\mathbb D)$. Thus, we can make the semi-direct product on 
$ \mathfrak{g}\mathfrak{l}(n,\mathbb D) \oplus_\iota \mathbb D^n$ by setting 
$ [(A,0), (0, v) ]:= (0, Av) $; see [Reference Knapp9, Chapter 1, Section 4, Example 2] for more details. As done for 
$ {\rm Aff} (n,\mathbb D) $ in Equation (3.1), consider the embedding
\begin{equation*} \Psi \colon \mathfrak{g}\mathfrak{l}(n,\mathbb D) \oplus_\iota \mathbb D^n \longrightarrow \mathfrak{g}\mathfrak{l}(n+1, \mathbb D) \quad \text{given}\ \text{by }\
\Psi ( (X,w)) = \begin{pmatrix} X & w \\
\mathbf{0} & 0
\end{pmatrix}.
\end{equation*} Then the image has the usual Lie algebra structure, and 
$\mathfrak{aff}(n, \mathbb D) := \mathfrak{g}\mathfrak{l}(n,\mathbb D) \oplus_\iota\mathbb D^n$ is the Lie algebra of the linear Lie group 
$\mathrm{Aff}(n,\mathbb D) $. Note that the adjoint action of 
$ G:=\mathrm{Aff}(n,\mathbb D) $ on its Lie algebra 
$\mathfrak{g}:= \mathfrak{aff}(n, \mathbb D)$ is given by
\begin{align}
{\rm Ad}\colon G \times \mathfrak{g} \longrightarrow \mathfrak{g} ; \qquad {\rm Ad}(A,v)\!\cdot\!(X,w) \,=\, \big(AXA^{-1},\, -(AXA^{-1})v + Aw \big).
\end{align} Now we recall the notion of adjoint reality for a linear Lie group G, which was introduced in [Reference Gongopadhyay and Maity7]. The adjoint action of a linear Lie group G on its Lie algebra 
$\mathfrak{g}$ is given by the conjugation, i.e., 
${\rm Ad}(g)X:=gXg^{-1}$. An element 
$X\in \mathfrak{g}$ is called AdG-real if 
$-X =gXg^{-1} $ for some 
$g\in G$. An AdG-real element 
$X\in \mathfrak{g}$ is called strongly AdG-real if 
$-X = \tau X \tau^{-1} $ for some involution 
$\tau\in G$; see [Reference Gongopadhyay and Maity7, Definition 1.1]. Observe that if 
$-X =gXg^{-1} $ for some 
$g\in G$, then 
$(\exp (X))^{-1} =g\,\exp (X)g^{-1} $. Thus, if 
$X\in \mathfrak{g}$ is AdG-real (respectively, strongly AdG-real), then 
$\exp (X)$ is reversible (respectively, strongly reversible) in G, [Reference Gongopadhyay and Maity7, Lemma 2.1]. But the converse is not true in general. For example, 
$X= \mathrm{diag}( 2 \pi \mathbf{i}, \pi \mathbf{i} ) \in \mathfrak{gl}(2, \mathbb C)$ is not 
$ {\rm Ad}_{\mathrm{GL}(2, \mathbb C)}$-real, but 
$g =\mathrm{diag}( 1, -1 ) = \exp (X) \in \mathrm{GL}(2, \mathbb C)$ is reversible.
We will investigate the 
$ {\rm Ad}_{\mathrm{Aff}(n,\mathbb D)}$-real elements in the Lie algebra 
$\mathfrak{aff}(n, \mathbb D)$. Next result gives necessary and sufficient conditions for the strongly 
$ {\rm Ad}_{\mathrm{Aff}(n,\mathbb D)}$-real elements in 
$ \mathfrak{aff}(n, \mathbb D)$. This can be thought of as a Lie algebra version of Lemma 3.3.
Lemma 3.8. Let 
$ (N,x) \in \mathfrak{aff}(n, \mathbb D)$ be an arbitrary element. Then (N, x) is strongly 
$ {\rm Ad}_{\mathrm{Aff}(n,\mathbb D) }$-real if and only if there exists an element 
$h = (B,w) \in \mathrm{Aff}(n,\mathbb D) $ such that both the following conditions hold:
(1)
$BNB^{-1} = -N$ and $ B^2 = \mathrm{I}_n$,(2)
$(B+\mathrm{I}_n)(w)=\mathbf{0}$ and $N(w)\,=\,-(B+\mathrm{I}_n)(x)$.
Proof. We omit the proof as it is identical to that of Lemma 3.3.
The following result will be used in proving Lemma 3.10.
Lemma 3.9. Let 
$ (N,x) \in \mathfrak{aff}(n, \mathbb D)$ such that 
$N= \mathrm{J}(0,\, n)$, where 
$ \mathbb D = \mathbb R, \mathbb C$ or 
$\mathbb H$. Then (N, x) is strongly 
$ {\rm Ad}_{\mathrm{Aff}(n,\mathbb D) }$-real.
Proof. For the element (N, x), consider 
$ B:= {\rm diag}((-1)^{n}, (-1)^{n-1}, \dots, 1,-1)_{n \times n} $. Then condition (1) of Lemma 3.8 holds. Further, by choosing the diagonal matrix B, the last row of N and 
$B+\mathrm{I}_n$ are equal to zero vector in 
$\mathbb D^n$. This implies that for every 
$x \in \mathbb D^n$, the last coordinate of 
$B+\mathrm{I}_n (x)$ is zero. Since the rank of N is n − 1, so equation 
$Nw=-(B+\mathrm{I}_n)(x)$ is consistent for given 
$x \in \mathbb D^n$ and has a solution. To prove this lemma, it is sufficient to choose 
$ w\in \mathbb D^n $ so that the condition (2) of Lemma 3.8 holds. This can be done in the following way:
(1) Let n be even. Then for
$x = [x_{k}]_{n \times 1} \in \mathbb D^n$, take $w = [w_{k}]_{n \times 1} \in \mathbb D^n $ such that
\begin{equation*}
w_{2k-1}= 0\quad \hbox{and }\quad w_{2k} =-2 x_{2k-1}, \ \hbox{where } k \in \left\{1,2,\ldots,\frac{n}{2} \right\}.
\end{equation*}Here, we get unique w depending on v for our choice of B.
(2) Let n be odd. Then for
$x = [x_{k}]_{n \times 1} \in \mathbb D^n$, take $w = [w_{k}]_{n \times 1} \in \mathbb D^n $ such that
\begin{equation*}
w_1 \in \mathbb D, \ w_{2k}= 0, \quad \hbox{and }\quad w_{2k+1} =-2 x_{2k}, \ \hbox{where } k \in \left\{1,2,\dots,\frac{n-1}{2} \right\}.
\end{equation*}Here, for our choice of B, we get no condition on w 1.
Then in view of Lemma 3.8, the element (N, x) is strongly 
$ {\rm Ad}_{\mathrm{Aff}(n,\mathbb D) }$-real. Hence, the proof follows.
The following lemma demonstrates that affine transformations with linear part conjugate to a unipotent Jordan block are strongly reversible.
Lemma 3.10. Let 
$ (A,v) \in \mathrm{Aff}(n,\mathbb D) $ such that 
$A= \mathrm{J}(1, \, n)$, where 
$ \mathbb D = \mathbb R, \mathbb C$ or 
$\mathbb H$. Then g is strongly reversible in 
$\mathrm{Aff}(n,\mathbb D) $.
Proof. Let 
$ N:= \mathrm{J}(0, \, n) \in \mathfrak{g}\mathfrak{l}(n,\mathbb D)$. Then 
$( \sigma, y) \exp((N,x)) (\sigma,y)^{-1} = (A, v) $ for some 
$(\sigma, y) \in \mathrm{Aff}(n,\mathbb D)$. Recall that the Lie algebra 
$\mathfrak{aff}(n, \mathbb D) = \mathfrak{g}\mathfrak{l}(n,\mathbb D) \oplus_\iota\mathbb D^n $. Using Lemma 3.9, we have that 
$ (N, x) \in \mathfrak{aff}(n, \mathbb D)$ is strongly 
$ {\rm Ad}_{\mathrm{Aff}(n,\mathbb D) }$-real. Let 
$ (\alpha, z) \in \mathrm{Aff}(n,\mathbb D)$ be an involution so that 
$ (\alpha, z) (N,x) (\alpha, z) = -(N, x)$. By taking the exponential, we have that 
$ (\alpha, z) \exp((N,x)) (\alpha, z)^{-1} = \exp(-(N, x))$. Let 
$g:= ( \sigma, y) (\alpha, z)( \sigma, y)^{-1} $. Then g is an involution in 
${\rm Aff }(n,\mathbb D) $ and 
$ g(A,v) g^{-1} = (A,v)^{-1}$; see [Reference Gongopadhyay and Maity7, Lemma 2.1]. This completes the proof.
The next result follows from Lemma 3.10, which will be crucially used in the proof of Theorem 1.1.
Proposition 3.11. Let 
$g = (A,v) \in \mathrm{Aff}(n,\mathbb D) $ such that A is a unipotent matrix, where 
$ \mathbb D = \mathbb R, \mathbb C$ or 
$\mathbb H$. Then g is strongly reversible in 
$\mathrm{Aff}(n,\mathbb D) $ and consequently g is also reversible in 
$\mathrm{Aff}(n,\mathbb D) $.
Proof. In view of Lemma 2.3, up to conjugacy in 
$\mathrm{GL}(n,\mathbb D)$, we can assume A as in Jordan form given by Equation (2.1). Using Lemma 3.10 and Example 3.1, we can construct a suitable 
$h = (B,w) \in \mathrm{Aff}(n,\mathbb D) $ such that 
$hgh^{-1}=g^{-1}$. Hence, g is strongly reversible in 
$\mathrm{Aff}(n,\mathbb D) $. This completes the proof.
3.4. Proof of Theorem 1.1
Let 
$g \in {\rm Aff}(n,\mathbb D)$ be an arbitrary element. Using Lemma 3.2 and Lemma 3.3, it follows that if g is reversible (respectively, strongly reversible) in 
$\mathrm{Aff}(n,\mathbb D) $ then A is reversible (respectively, strongly reversible) in 
$\mathrm{GL}(n,\mathbb D)$.
Conversely, using Lemma 3.4, up to conjugacy, we can assume that 
$ g = (A,v) \in {\rm Aff}(n,\mathbb D)$ such that
\begin{equation}
A =\begin{pmatrix} T & \\
& U
\end{pmatrix}, \qquad v = \begin{pmatrix} \mathbf{0}_{n-m} \\
\tilde{v}
\end{pmatrix},
\end{equation} where 
$0 \leq m \leq n$, 
$ \mathbf{0}_{n-m} $ denotes the zero vector in 
$\mathbb D^{n-m}$ and 
$T \in \mathrm{GL}(n-m,\mathbb D)$, 
$U \in \mathrm{GL}(m,\mathbb D)$ such that T does not have eigenvalue 1, U has only 1 as eigenvalue and 
$ \tilde{v} = [v_1,v_2,\dots,v_m] \in \mathbb D^m$. Here, T and U do not have a common eigenvalue. This implies that if 
$B \in \mathrm{GL}(n,\mathbb D)$ is such that 
$BAB^{-1}=A^{-1}$, then B has the following form
\begin{equation*}B=\begin{pmatrix} B_1 & \\
& B_2
\end{pmatrix}, \ \hbox{where } B_1 \in \mathrm{GL}(n-m,\mathbb D),\ B_2 \in \mathrm{GL}(m,\mathbb D).
\end{equation*} Therefore, if A is reversible (respectively, strongly reversible) in 
$\mathrm{GL}(n,\mathbb D)$, then 
$T \in \mathrm{GL}(n-m,\mathbb D)$ and 
$U \in \mathrm{GL}(m,\mathbb D)$ are reversible (respectively, strongly reversible). Consider 
$h= (U,\tilde{v}) \in {\rm Aff}(m,\mathbb D)$, where U is a unipotent matrix. Then Proposition 3.11 implies that h is strongly reversible in 
${\rm Aff}(m,\mathbb D)$. Proof of the converse part now follows from Equation (3.5).
Further, for the case 
$\mathbb D= \mathbb R $ or 
$\mathbb C$, Proposition 2.4 implies that g is reversible in 
$ {\rm Aff }(n,\mathbb D) $ if and only if g is strongly reversible in 
$ {\rm Aff }(n,\mathbb D) $. This completes the proof.
4. Product of involutions in $\mathrm{Aff}(n,\mathbb D) $
In this section, we investigate the involution length in the group 
$\mathrm{Aff}(n,\mathbb D) $. We shall begin by recalling the basic concept of determinant for matrices over 
$ \mathbb H $. For 
$A \in \mathrm{M}(n,\mathbb H)$, let 
$ A = (A_1) + (A_2) \mathbf{j} $ for some 
$ A_1, A_2 \in \mathrm{M}(n,\mathbb C)$. Consider the embedding 
$ \Phi: \mathrm{M}(n,\mathbb H) \longrightarrow \mathrm{M}(2n,\mathbb C)$ defined as
\begin{equation}
\Phi(A) = \begin{pmatrix} A_1 & A_2 \\
- \overline{A_2} & \overline{A_1}
\end{pmatrix}\,,
\end{equation} where 
$ \overline{A_j} $ denotes the complex conjugate of Aj.
Definition 4.1. For 
$A \in \mathrm{M}(n,\mathbb H)$, determinant of A is defined as the determinant of corresponding matrix 
$ \Phi(A)$, i.e., 
$ {\rm det}(A):= {\rm det}(\Phi(A))$, where Φ is as defined in Equation (4.1); see [Reference Rodman12, Section 5.9]. In view of the Skolem–Noether theorem, the above definition is independent of the choice of the chosen embedding Φ.
Recall that if 
$h =(B,v) \in \mathrm{Aff}(n,\mathbb D)$ is an involution, then B has to be an involution in 
$\mathrm{GL}(n,\mathbb D)$; see Lemma 3.3. If an element of 
$\mathrm{GL}(n,\mathbb D)$ is a product of involutions, then necessarily its determinant is either 1 or −1. Product of involutions in 
$\mathrm{GL}(n,\mathbb D)$ has been studied in [Reference Gustafson, Halmos and Radjavi8] and [Reference O’Farrell and Short11, Section 4.2.4] for the case 
$ \mathbb D=\mathbb R$ or 
$\mathbb C$.
In the next result, we investigate the product of involutions in 
$\mathrm{GL}(n,\mathbb D)$.
Lemma 4.2. Let 
$ \mathbb D=\mathbb R, \mathbb C $ or 
$\mathbb H$. Every element of 
$\mathrm{GL}(n,\mathbb D)$ with determinant 1 or −1 can be written as a product of at most four involutions.
Proof. Using the Jordan decomposition over 
$\mathbb H$, up to conjugacy, we can assume that every element of 
$\mathrm{GL}(n,\mathbb H)$ is in 
$\mathrm{GL}(n,\mathbb C)$; see [Reference Rodman12,
Theorem 5.5.3]. The proof now follows from [Reference O’Farrell and Short11, Theorem 4.9].
Remark 4.3. Note that an element of a group G is strongly reversible if and only if it can be expressed as a product of two involutions in G; see [Reference O’Farrell and Short11, Proposition 2.12].
Next, we will prove Theorem 1.2.
Proof of Theorem 1.2
Let 
$ g = (A,v) \in {\rm Aff}(n,\mathbb D) $ be such that 
$ \mathrm{det}(A) \in \{-1, 1\}$. Then using Lemma 3.4, up to conjugacy, we can assume that
\begin{equation}
A =\begin{pmatrix} T & \\
& U
\end{pmatrix}, \qquad v = \begin{pmatrix} \mathbf{0}_{n-m} \\
\tilde{v}
\end{pmatrix},
\end{equation} where 
$T \in \mathrm{GL}(n-m,\mathbb D)$ and 
$U \in \mathrm{GL}(m,\mathbb D)$ such that T does not have eigenvalue 1 and U has only 1 as eigenvalue. Here, 
$0\leq m \leq n$, 
$ \mathbf{0}_{n-m} $ denotes the zero vector in 
$\mathbb D^{n-m}$ and 
$ \tilde{v} = [v_1,v_2,\dots,v_m] \in \mathbb D^m$. Consider 
$h = (U,\tilde{v} ) \in {\rm Aff}(m,\mathbb D) $. Using Proposition 3.11, h is strongly reversible in 
${\rm Aff}(m,\mathbb D) $. Therefore, in view of Remark 4.3, there exist involutions 
$h_1 = (P,u)$ and 
$h_2 = (Q,w)$ in 
${\rm GL}(m,\mathbb D) \ltimes \mathbb D^m $ such that
\begin{equation}
h = h_1 \, h_2.
\end{equation} Further, note that 
$\mathrm{det}(A)= \mathrm{det}(T) \, \mathrm{det}(U) = \mathrm{det}(T)$. Thus, 
$T \in {\rm GL}(n-m,\mathbb D)$ has determinant either 1 or −1. In view of Lemma 4.2, we have
\begin{equation}
T= B_1 B_2 B_3 B_4,
\end{equation} where Bi is an involution in 
${\rm GL}(n-m,\mathbb D)$ for all 
$i \in \{1,2,3,4\}$. Here, Bi may be equal to 
$\mathrm{I}_{n-m}$ for some 
$i \in \{1,2,3,4\}$. Now consider the following elements in 
${\rm Aff}(n,\mathbb D) $:
•
$f_1 := ( B_1 \oplus \mathrm{I}_m, \mathbf{0}_{n}),$•
$ f_2 := ( B_2 \oplus \mathrm{I}_m, \mathbf{0}_{n}), $•
$ f_3 := ( B_3 \oplus P, \mathbf{0}_{n-m} \oplus u), $•
$ f_4 := ( B_4 \oplus Q, \mathbf{0}_{n-m} \oplus w)$.
From the above construction, it is clear that f 1, f 2, f 3, and f 4 are involutions in 
${\rm Aff}(n,\mathbb D) $. Using Equations (4.2), (4.3) and (4.4), we have 
$ g= f_1 f_2 f_3 f_4$. This completes the proof.
Funding Statement
Gongopadhyay is partially supported by the SERB core research grant CRG/2022/003680. Lohan acknowledges support from the CSIR SRF grant, File No. : 09/947(0113)/2019-EMR-I. Maity is supported by an NBHM PDF during this work.
