Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-06-14T20:32:06.105Z Has data issue: false hasContentIssue false
  • English
  • Français

Counting elements of the congruence subgroup

Part of: Special matrices Polynomials and matrices

Published online by Cambridge University Press:  22 May 2024

Kamil Bulinski  and
Igor E. Shparlinski Open the ORCID record for Igor E. Shparlinski [Opens in a new window]
Kamil Bulinski
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney, UNSW 2052, Australia e-mail: k.bulinski@unsw.edu.au
Igor E. Shparlinski*
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney, UNSW 2052, Australia e-mail: k.bulinski@unsw.edu.au
*
e-mail: igor.shparlinski@unsw.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

We obtain asymptotic formulas for the number of matrices in the congruence subgroup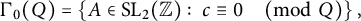

$$\begin{align*}\Gamma_0(Q) = \left\{ A\in\operatorname{SL}_2({\mathbb Z}):~c \equiv 0 \quad\pmod Q\right\}, \end{align*}$$
which are of naive height at most X. Our result is uniform in a very broad range of values Q and X.

Keywords

SL2(ℤ) matricescongruence subgroupmodular hyperbola

MSC classification

Primary: 11C20: Matrices, determinants 15B36: Matrices of integers 15B52: Random matrices
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 15
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

During the preparation of this work, the authors were supported in part by the Australian Research Council Grants DP230100530 and DP230100534.

References

Baier, S., Multiplicative inverses in short intervals . Int. J. Number Theory 9(2013), 877–884.CrossRefGoogle Scholar
Browning, T. D. and Haynes, A., Incomplete Kloosterman sums and multiplicative inverses in short intervals . Int. J. Number Theory 9(2013), 481–486.CrossRefGoogle Scholar
Bulinski, K., Ostafe, A., and Shparlinski, I. E., Counting embeddings of free groups into ${SL}_2\left(\mathbb{Z}\right)$ and its subgroups . Ann. Sc. Norm. Pisa, (to appear).Google Scholar
Chan, T. H., Shortest distance in modular hyperbola and least quadratic non-residue . Mathematika 62(2016), 860–865.CrossRefGoogle Scholar
Garaev, M. Z. and Shparlinski, I. E., On the distribution of modular inverses from short intervals. Mathematika 69(2023), 1183–1194.CrossRefGoogle Scholar
Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers, Oxford University Press, Oxford, 2008.CrossRefGoogle Scholar
Humphries, P., Distributing points on the torus via modular inverses . Quart. J. Math. 73(2022), 1–16.CrossRefGoogle Scholar
Iwaniec, H., Topics in classical automorphic forms, Graduate Studies in Mathematics, 17, American Mathematical Society, Providence, RI, 1997.CrossRefGoogle Scholar
Krieg, A., Counting modular matrices with specified maximum norm . Linear Algebra Appl. 196(1994), 273–278.Google Scholar
Newman, M., Counting modular matrices with specified Euclidean norm . J. Combin. Theory Ser. A 47(1988), 145–149.Google Scholar
Shapiro, H. N., Introduction to the theory of numbers, Wiley, New York, 1983.Google Scholar
Shparlinski, I. E., Modular hyperbolas . Jpn. J. Math. 7(2012), 235–294.Google Scholar
Suryanarayana, D., The greatest divisor of $n$ which is prime to $k$ . Math. Student 37(1969), 147–157.Google Scholar
Ustinov, A. V., On the number of solutions of the congruence $xy\equiv \ell\;({\mathrm{mod}}\;q)$ under the graph of a twice continuously differentiable function . St. Petersburg Math. J. 20(2009), 813–836 (translated from Algebra i Analiz).Google Scholar
Ustinov, A. V., On points of the modular hyperbola under the graph of a linear function . Math. Notes 97(2015), 284–288 (translated from Matem. Zametki).CrossRefGoogle Scholar