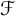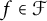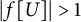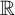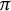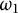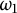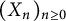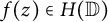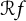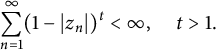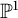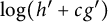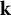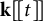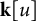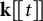FirstView articles
Article
Adjoint Reidemeister torsions of some 3-manifolds obtained by Dehn surgeries
- Part of:
-
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-15
-
- Article
- Export citation
Li coefficients and the quadrilateral zeta function
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2024, pp. 1-12
-
- Article
- Export citation
Existence of singular rotationally symmetric gradient Ricci solitons in higher dimensions
- Part of:
-
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1-18
-
- Article
- Export citation
Almost sure convergence of the
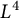 $L^4$ norm of Littlewood polynomials
$L^4$ norm of Littlewood polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 15 March 2024, pp. 1-14
-
- Article
- Export citation
Ideals with componentwise linear powers
- Part of:
-
- Published online by Cambridge University Press:
- 12 March 2024, pp. 1-9
-
- Article
- Export citation
A class of Hessian quotient equations in de Sitter space
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1-17
-
- Article
- Export citation
Linear independence of series related to the Thue–Morse sequence along powers
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1-11
-
- Article
- Export citation
Moments of the central L-values of the Asai lifts
- Part of:
-
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-9
-
- Article
- Export citation
On the complexity of extending the convergence domain of Newton’s method under the weak majorant condition
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2024, pp. 1-15
-
- Article
- Export citation
Hausdorff operators on some classical spaces of analytic functions
- Part of:
-
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1-13
-
- Article
- Export citation
The degree one Laguerre–Pólya class and the shuffle-word-embedding conjecture
- Part of:
-
- Published online by Cambridge University Press:
- 28 February 2024, pp. 1-8
-
- Article
- Export citation
Theoretical study of a
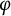 $\varphi $-Hilfer fractional differential system in Banach spaces
$\varphi $-Hilfer fractional differential system in Banach spaces
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2024, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral equivariant cohomology of affine Grassmannians
- Part of:
-
- Published online by Cambridge University Press:
- 08 February 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some examples of noncommutative projective Calabi–Yau schemes
- Part of:
-
- Published online by Cambridge University Press:
- 08 February 2024, pp. 1-21
-
- Article
- Export citation
Nowhere constant families of maps and resolvability
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2024, pp. 1-5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Borel reducibility of equivalence relations on
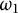 $\omega _1$
$\omega _1$
- Part of:
-
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A characterization of random analytic functions satisfying Blaschke-type conditions
- Part of:
-
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1-10
-
- Article
- Export citation
Relations for quadratic Hodge integrals via stable maps
- Part of:
-
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral mean estimates for univalent and locally univalent harmonic mappings
- Part of:
-
- Published online by Cambridge University Press:
- 15 January 2024, pp. 1-15
-
- Article
- Export citation
How to determine a curve singularity
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation





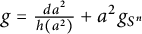
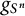
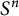
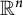
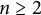
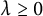
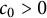
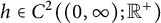
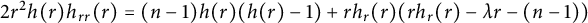
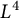
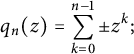
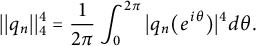
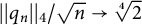
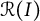
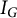
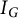
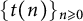
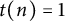
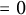
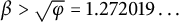
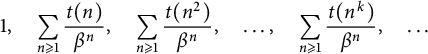
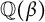
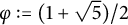
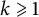
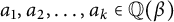
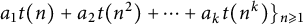
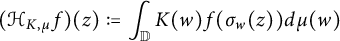
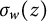
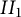
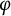
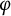
 .
.