1 Introduction
The main aim of this note is to provide a simple presentation, in terms of generators and relations, of the torus-equivariant cohomology of the affine Grassmannian and flag variety,
![]() $\widetilde {\mathrm {Gr}}_n$
and
$\widetilde {\mathrm {Gr}}_n$
and
![]() $\widetilde {\mathrm {Fl}}_n$
. In particular, we obtain these rings as quotients of polynomial rings, with the quotient map arising geometrically as the pullback via embeddings in the Sato Grassmannian and flag variety, respectively.
$\widetilde {\mathrm {Fl}}_n$
. In particular, we obtain these rings as quotients of polynomial rings, with the quotient map arising geometrically as the pullback via embeddings in the Sato Grassmannian and flag variety, respectively.
Let ![]() be the polynomial ring in countably many generators, with
be the polynomial ring in countably many generators, with
![]() $c_i$
in degree
$c_i$
in degree
![]() $2i$
. Let
$2i$
. Let
![]() $p_k=p_k(c)$
be the polynomial
$p_k=p_k(c)$
be the polynomial
 $$ \begin{align} p_k(c) = (-1)^{k-1} \det \left(\begin{array}{ccccc} c_1 & 1 & 0 & 0 & 0 \\ 2c_2 & c_1 & 1 & 0 & 0 \\ 3c_3 & c_2 & \ddots & \ddots & 0 \\ \vdots & \vdots & \ddots & \ddots & 1 \\kc_k & c_{k-1} & \cdots & c_2 & c_1 \end{array}\right). \end{align} $$
$$ \begin{align} p_k(c) = (-1)^{k-1} \det \left(\begin{array}{ccccc} c_1 & 1 & 0 & 0 & 0 \\ 2c_2 & c_1 & 1 & 0 & 0 \\ 3c_3 & c_2 & \ddots & \ddots & 0 \\ \vdots & \vdots & \ddots & \ddots & 1 \\kc_k & c_{k-1} & \cdots & c_2 & c_1 \end{array}\right). \end{align} $$
One can identify
![]() $\Lambda $
with the ring of symmetric functions in some other set of variables, making
$\Lambda $
with the ring of symmetric functions in some other set of variables, making
![]() $c_k$
the complete homogeneous symmetric function, so that
$c_k$
the complete homogeneous symmetric function, so that
![]() $p_k$
becomes the power sum symmetric function via the Newton relations. But until Section 3 we remain agnostic about the choice of such an identification.
$p_k$
becomes the power sum symmetric function via the Newton relations. But until Section 3 we remain agnostic about the choice of such an identification.
Fixing n, consider the polynomials
 $$ \begin{align} &\qquad\qquad\qquad\qquad + p_2(c)\, e_{k-2}(y_1,\ldots,y_n) + p_1(c)\, e_{k-1}(y_1,\ldots,y_n) \nonumber \\ &\qquad\qquad\quad\qquad= \sum_{i=1}^k p_{i}(c)\, e_{k-i}(y_1,\ldots,y_n) \end{align} $$
$$ \begin{align} &\qquad\qquad\qquad\qquad + p_2(c)\, e_{k-2}(y_1,\ldots,y_n) + p_1(c)\, e_{k-1}(y_1,\ldots,y_n) \nonumber \\ &\qquad\qquad\quad\qquad= \sum_{i=1}^k p_{i}(c)\, e_{k-i}(y_1,\ldots,y_n) \end{align} $$
in
![]() $\Lambda [y_1,\ldots ,y_n]$
, where
$\Lambda [y_1,\ldots ,y_n]$
, where
![]() $e_i(y_1,\ldots ,y_n)$
is the elementary symmetric polynomial in the indicated variables.
$e_i(y_1,\ldots ,y_n)$
is the elementary symmetric polynomial in the indicated variables.
Let V be a complex vector space with basis
![]() $\mathrm {e}_i$
, for
$\mathrm {e}_i$
, for ![]() , and let
, and let
![]() $V_{\leq 0}$
be the subspace spanned by
$V_{\leq 0}$
be the subspace spanned by
![]() $\mathrm {e}_i$
for
$\mathrm {e}_i$
for
![]() $i\leq 0$
. The torus
$i\leq 0$
. The torus ![]() acts by scaling the basis vector
acts by scaling the basis vector
![]() $\mathrm {e}_i$
by the character
$\mathrm {e}_i$
by the character
![]() $y_{{i\pmod n}}$
, using representatives
$y_{{i\pmod n}}$
, using representatives
![]() $1,\ldots ,n$
for residues mod n. Let
$1,\ldots ,n$
for residues mod n. Let
![]() $\mathrm {Gr}^d=\mathrm {Gr}^d(V)$
be the corresponding Sato Grassmannian parameterizing subspaces of index d, with the induced action of
$\mathrm {Gr}^d=\mathrm {Gr}^d(V)$
be the corresponding Sato Grassmannian parameterizing subspaces of index d, with the induced action of
![]() ${T}$
. The dth component of the affine Grassmannian embeds
${T}$
. The dth component of the affine Grassmannian embeds
![]() ${T}$
-equivariantly in
${T}$
-equivariantly in
![]() $\mathrm {Gr}^d$
. (Definitions of these spaces are reviewed in Section 2 below.) We write
$\mathrm {Gr}^d$
. (Definitions of these spaces are reviewed in Section 2 below.) We write ![]() for the tautological bundle on
for the tautological bundle on
![]() $\mathrm {Gr}^d$
, and recycle the same notation for the tautological bundle on subvarieties, when the context is clear.
$\mathrm {Gr}^d$
, and recycle the same notation for the tautological bundle on subvarieties, when the context is clear.
The equivariant cohomology of the Sato Grassmannian is
![]() $H_{{T}}^*\mathrm {Gr}^d = \Lambda [y_1,\ldots ,y_n]$
, identifying
$H_{{T}}^*\mathrm {Gr}^d = \Lambda [y_1,\ldots ,y_n]$
, identifying
![]() $c_k$
with the Chern class
$c_k$
with the Chern class ![]() .
.
Theorem The inclusion
![]() $\widetilde {\mathrm {Gr}}^d_n \hookrightarrow \mathrm {Gr}^d$
induces a surjection
$\widetilde {\mathrm {Gr}}^d_n \hookrightarrow \mathrm {Gr}^d$
induces a surjection
![]() $H_{{T}}^*\mathrm {Gr}^d \twoheadrightarrow H_{{T}}^*\widetilde {\mathrm {Gr}}^d_n$
, whose kernel is generated by
$H_{{T}}^*\mathrm {Gr}^d \twoheadrightarrow H_{{T}}^*\widetilde {\mathrm {Gr}}^d_n$
, whose kernel is generated by
![]() $p_k(c|y)$
for
$p_k(c|y)$
for
![]() $k> n$
, together with
$k> n$
, together with
![]() $p_n(c|y)+d e_n(y)$
.
$p_n(c|y)+d e_n(y)$
.
In particular, the map ![]() defines an isomorphism of
defines an isomorphism of ![]() -algebras
-algebras
where
![]() $I_n^d$
is the ideal generated by
$I_n^d$
is the ideal generated by
![]() $p_k(c|y)$
for
$p_k(c|y)$
for
![]() $k> n$
and
$k> n$
and
![]() $p_n(c|y)+d e_n(y)$
.
$p_n(c|y)+d e_n(y)$
.
All the generators of
![]() $I_n^d$
are symmetric in the y variables. It follows that the
$I_n^d$
are symmetric in the y variables. It follows that the
![]() $GL_n$
-equivariant cohomology has essentially the same presentation. Write
$GL_n$
-equivariant cohomology has essentially the same presentation. Write ![]() , with
, with
![]() $e_k$
in degree
$e_k$
in degree
![]() $2k$
, regarded as a subring of
$2k$
, regarded as a subring of
![]() $H_{{T}}^*(\mathrm {pt})$
by sending
$H_{{T}}^*(\mathrm {pt})$
by sending
![]() $e_k$
to the elementary symmetric polynomial
$e_k$
to the elementary symmetric polynomial
![]() $e_k(y)$
. Define elements
$e_k(y)$
. Define elements
![]() $p_k(c|e) \in \Lambda [e_1,\ldots ,e_n]$
by the same formula (1.3), with
$p_k(c|e) \in \Lambda [e_1,\ldots ,e_n]$
by the same formula (1.3), with
![]() $e_k=0$
for
$e_k=0$
for
![]() $k>n$
.
$k>n$
.
Corollary A Let
![]() $J_n^d \subset \Lambda [e_1,\ldots ,e_n]$
be the ideal generated by
$J_n^d \subset \Lambda [e_1,\ldots ,e_n]$
be the ideal generated by
![]() $p_k(c|e)$
for
$p_k(c|e)$
for
![]() $k>n$
and
$k>n$
and
![]() $p_n(c|e)+ de_n$
. Then the map
$p_n(c|e)+ de_n$
. Then the map ![]() defines an isomorphism of
defines an isomorphism of
![]() $H_{GL_n}^*(\mathrm {pt})$
-algebras
$H_{GL_n}^*(\mathrm {pt})$
-algebras
This follows from the theorem by an application of the general fact that
![]() $H_{GL_n}^*X \subset H_{{T}}^*X$
is the invariant ring for the natural
$H_{GL_n}^*X \subset H_{{T}}^*X$
is the invariant ring for the natural
![]() $\mathcal {S}_n$
action on y variables (see, e.g., [Reference Anderson and FultonAF, Section 15.6]).
$\mathcal {S}_n$
action on y variables (see, e.g., [Reference Anderson and FultonAF, Section 15.6]).
A presentation for the equivariant cohomology of
![]() $\widetilde {\mathrm {Fl}}_n$
also follows from the theorem. Let
$\widetilde {\mathrm {Fl}}_n$
also follows from the theorem. Let ![]() be the tautological flag on
be the tautological flag on
![]() $\widetilde {\mathrm {Fl}}_n$
.
$\widetilde {\mathrm {Fl}}_n$
.
Corollary B Evaluating ![]() and
and ![]() , we have
, we have
where
![]() $I^{\mathrm {Fl}}_n$
is generated by
$I^{\mathrm {Fl}}_n$
is generated by
![]() $p_k(c|y)$
for
$p_k(c|y)$
for
![]() $k\geq n$
along with
$k\geq n$
along with
![]() $e_i(x)-e_i(y)$
for
$e_i(x)-e_i(y)$
for
![]() $i=1,\ldots ,n$
.
$i=1,\ldots ,n$
.
For
![]() $GL_n$
-equivariant cohomology, the presentation is similar:
$GL_n$
-equivariant cohomology, the presentation is similar:
where
![]() $J^{\mathrm {Fl}}_n$
is generated by
$J^{\mathrm {Fl}}_n$
is generated by
![]() $p_k(c|e)$
for
$p_k(c|e)$
for
![]() $k\geq n$
along with
$k\geq n$
along with
![]() $e_i(x)-e_i$
for
$e_i(x)-e_i$
for
![]() $i=1,\ldots ,n$
.
$i=1,\ldots ,n$
.
This can be deduced from the theorem by examining the action of the shift morphism on cohomology (see Section 2).
A presentation for the non-equivariant cohomology ring
![]() $H^*\widetilde {\mathrm {Gr}}^0_n$
was given by Bott [Reference BottBo], who used a natural coproduct structure to identify this ring with the infinite symmetric power of the cohomology of projective space. Since
$H^*\widetilde {\mathrm {Gr}}^0_n$
was given by Bott [Reference BottBo], who used a natural coproduct structure to identify this ring with the infinite symmetric power of the cohomology of projective space. Since ![]() , this is easily seen to be equivalent to the result of setting the y variables to
, this is easily seen to be equivalent to the result of setting the y variables to
![]() $0$
in the statement of the main theorem above. (One makes the indicated identifications with symmetric functions in variables
$0$
in the statement of the main theorem above. (One makes the indicated identifications with symmetric functions in variables
![]() $\xi _1,\xi _2,\ldots $
, and Bott’s relations become
$\xi _1,\xi _2,\ldots $
, and Bott’s relations become
![]() $p_k(\xi )=0$
for
$p_k(\xi )=0$
for
![]() $k\geq n$
.)
$k\geq n$
.)
Several authors have given different presentations of the equivariant cohomology ring, sometimes with field coefficients, using localization or representation theory [Reference Lam and ShimozonoLS, Reference YunY, Reference Yun and ZhuYZ]. In the context of the moduli stack of vector bundles on ![]() , Larson described the integral cohomology ring as a subring of a polynomial ring with rational coefficients [Reference LarsonLa]. In fact, Larson’s description is equivalent to the quotient ring appearing in Corollary A; the precise translation is given in Section 6 below.
, Larson described the integral cohomology ring as a subring of a polynomial ring with rational coefficients [Reference LarsonLa]. In fact, Larson’s description is equivalent to the quotient ring appearing in Corollary A; the precise translation is given in Section 6 below.
In this note, the main contributions are to provide a concise presentation of
![]() $H_{{T}}^*\widetilde {\mathrm {Gr}}_n^d$
as a quotient of a polynomial ring, and to show how Bott’s method extends naturally to the equivariant setting. We also describe a new basis of double monomial symmetric functions which are well-adapted to the presentation of
$H_{{T}}^*\widetilde {\mathrm {Gr}}_n^d$
as a quotient of a polynomial ring, and to show how Bott’s method extends naturally to the equivariant setting. We also describe a new basis of double monomial symmetric functions which are well-adapted to the presentation of
![]() $H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
. Apart from some elementary calculations with symmetric functions, the only additional input required is a well-known presentation of the equivariant cohomology of projective space.
$H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
. Apart from some elementary calculations with symmetric functions, the only additional input required is a well-known presentation of the equivariant cohomology of projective space.
2 Infinite and affine flag varieties
We follow [Reference AndersonA], which in turn is based on [Reference Lam, Lee and ShimozonoLLS, Reference Pressley and SegalPS] (see also [Reference Sato and SatoSS]). As in the introduction, V is a complex vector space with basis
![]() $\mathrm {e}_i$
for
$\mathrm {e}_i$
for ![]() . For any interval
. For any interval
![]() $[a,b]$
in
$[a,b]$
in ![]() , we write
, we write
![]() $V_{[a,b]}$
for the subspace spanned by
$V_{[a,b]}$
for the subspace spanned by
![]() $\mathrm {e}_i$
for i in
$\mathrm {e}_i$
for i in
![]() $[a,b]$
. We will especially use subspaces
$[a,b]$
. We will especially use subspaces
![]() $V_{\leq p}$
(or
$V_{\leq p}$
(or
![]() $V_{>q}$
), spanned by
$V_{>q}$
), spanned by
![]() $\mathrm {e}_i$
for
$\mathrm {e}_i$
for
![]() $i\leq p$
(or
$i\leq p$
(or
![]() $i>q$
, respectively).
$i>q$
, respectively).
2.1 Definitions
The Sato Grassmannian
![]() $\mathrm {Gr}^d$
is the set of subspaces
$\mathrm {Gr}^d$
is the set of subspaces
![]() $E\subset V$
of index d. This means (1)
$E\subset V$
of index d. This means (1)
![]() $V_{\leq -m} \subset E \subset V_{\leq m}$
for some (and hence all)
$V_{\leq -m} \subset E \subset V_{\leq m}$
for some (and hence all)
![]() $m\gg 0$
, and (2)
$m\gg 0$
, and (2)
![]() $\dim E/(V_{\leq 0} \cap E) - \dim V_{\leq 0}/(V_{\leq 0}\cap E) = d$
. The Sato Grassmannian is naturally topologized as an ind-variety.
$\dim E/(V_{\leq 0} \cap E) - \dim V_{\leq 0}/(V_{\leq 0}\cap E) = d$
. The Sato Grassmannian is naturally topologized as an ind-variety.
The Sato flag variety is the subvariety ![]() consisting of chains of subspaces
consisting of chains of subspaces ![]() , with
, with
![]() $E_d\subset V$
belonging to
$E_d\subset V$
belonging to
![]() $\mathrm {Gr}^d$
. It is naturally a pro-ind-variety, and comes with projection morphisms
$\mathrm {Gr}^d$
. It is naturally a pro-ind-variety, and comes with projection morphisms
![]() $\pi _d \colon \mathrm {Fl} \to \mathrm {Gr}^d\kern-1.2pt$
.
$\pi _d \colon \mathrm {Fl} \to \mathrm {Gr}^d\kern-1.2pt$
.
The shift automorphism
![]() $\operatorname {\mathrm {sh}}\colon V \to V$
, defined by
$\operatorname {\mathrm {sh}}\colon V \to V$
, defined by
![]() $\mathrm {e}_i\mapsto \mathrm {e}_{i-1}$
, induces an automorphism of
$\mathrm {e}_i\mapsto \mathrm {e}_{i-1}$
, induces an automorphism of
![]() $\mathrm {Fl}$
, by
$\mathrm {Fl}$
, by ![]() . For a fixed positive n, the affine flag variety is the fixed locus of
. For a fixed positive n, the affine flag variety is the fixed locus of
![]() $\operatorname {\mathrm {sh}}^n$
:
$\operatorname {\mathrm {sh}}^n$
:
The affine Grassmannian is the image of
![]() $\widetilde {\mathrm {Fl}}_n$
under the projection map:
$\widetilde {\mathrm {Fl}}_n$
under the projection map:
A torus ![]() acts on V by scaling the coordinate
acts on V by scaling the coordinate
![]() $\mathrm {e}_i$
by the character
$\mathrm {e}_i$
by the character
![]() $y_i$
. This induces actions on
$y_i$
. This induces actions on
![]() $\mathrm {Fl}$
and
$\mathrm {Fl}$
and
![]() $\mathrm {Gr}^d$
. We cyclically embed
$\mathrm {Gr}^d$
. We cyclically embed ![]() in
in ![]() , by specializing characters
, by specializing characters
![]() $y_i \mapsto y_{i\pmod n}$
, using representatives
$y_i \mapsto y_{i\pmod n}$
, using representatives
![]() $1,\ldots ,n$
for residues mod n. So
$1,\ldots ,n$
for residues mod n. So ![]() is the fixed subgroup for the automorphism induced by
is the fixed subgroup for the automorphism induced by
![]() $\operatorname {\mathrm {sh}}^n$
, and
$\operatorname {\mathrm {sh}}^n$
, and
![]() ${T}$
therefore acts on
${T}$
therefore acts on
![]() $\widetilde {\mathrm {Fl}}_n$
and
$\widetilde {\mathrm {Fl}}_n$
and
![]() $\widetilde {\mathrm {Gr}}_n^d$
.
$\widetilde {\mathrm {Gr}}_n^d$
.
The
![]() ${T}$
-fixed points of
${T}$
-fixed points of
![]() $\mathrm {Fl}$
(which are the same as the
$\mathrm {Fl}$
(which are the same as the ![]() -fixed points) are indexed by the set
-fixed points) are indexed by the set
![]() $\operatorname {\mathrm {Inj}}^0$
consisting of all injections
$\operatorname {\mathrm {Inj}}^0$
consisting of all injections ![]() such that
such that
and both these cardinalities are finite.Footnote
1
The flag ![]() corresponding to
corresponding to
![]() $w\in \operatorname {\mathrm {Inj}}^0$
consists of subspaces
$w\in \operatorname {\mathrm {Inj}}^0$
consists of subspaces
![]() $E_k$
spanned by
$E_k$
spanned by
![]() $\mathrm {e}_{w(i)}$
for
$\mathrm {e}_{w(i)}$
for
![]() $i\leq k$
, together with all
$i\leq k$
, together with all
![]() $\mathrm {e}_j$
for
$\mathrm {e}_j$
for
![]() $j\leq 0$
not in the image of w. The condition defining
$j\leq 0$
not in the image of w. The condition defining
![]() $\operatorname {\mathrm {Inj}}^0$
guarantees
$\operatorname {\mathrm {Inj}}^0$
guarantees ![]() lies in
lies in
![]() $\mathrm {Fl}$
. (See [Reference AndersonA, Section 6].)
$\mathrm {Fl}$
. (See [Reference AndersonA, Section 6].)
The
![]() ${T}$
-fixed points of
${T}$
-fixed points of
![]() $\widetilde {\mathrm {Fl}}_n$
are indexed by the group of affine permutations. This is the group
$\widetilde {\mathrm {Fl}}_n$
are indexed by the group of affine permutations. This is the group
![]() $\widetilde {\mathcal {S}}_n$
consisting of bijections w from
$\widetilde {\mathcal {S}}_n$
consisting of bijections w from ![]() to itself, such that
to itself, such that
![]() $w(i+n)=w(i)+n$
for all
$w(i+n)=w(i)+n$
for all ![]() , and such that
, and such that
![]() $\sum _{i=1}^n w(i) = \binom {n}{2}$
. Among many other equivalent descriptions, this is the subset of n-shift-invariant elements in
$\sum _{i=1}^n w(i) = \binom {n}{2}$
. Among many other equivalent descriptions, this is the subset of n-shift-invariant elements in
![]() $\operatorname {\mathrm {Inj}}^0$
:
$\operatorname {\mathrm {Inj}}^0$
:
Similarly,
![]() $GL_n$
acts on V, extending the standard action on
$GL_n$
acts on V, extending the standard action on ![]() by blocks, so
by blocks, so
![]() $V = \cdots \oplus V_{[-n+1,0]}\oplus V_{[1,n]}\oplus V_{[n+1,2n]}\oplus \cdots $
. This induces actions on the Sato and affine flag varieties and Grassmannians.
$V = \cdots \oplus V_{[-n+1,0]}\oplus V_{[1,n]}\oplus V_{[n+1,2n]}\oplus \cdots $
. This induces actions on the Sato and affine flag varieties and Grassmannians.
Often we will omit the superscript when focusing on the degree
![]() $d=0$
component, writing
$d=0$
component, writing
![]() $\mathrm {Gr} = \mathrm {Gr}^0$
and
$\mathrm {Gr} = \mathrm {Gr}^0$
and
![]() $\widetilde {\mathrm {Gr}}_n = \widetilde {\mathrm {Gr}}_n^0$
.
$\widetilde {\mathrm {Gr}}_n = \widetilde {\mathrm {Gr}}_n^0$
.
2.2 Chern classes and cohomology
We write ![]() in
in
![]() $H_{{T}}^*\mathrm {Gr}^d$
, and we use the same notation for the pullbacks to other varieties. For
$H_{{T}}^*\mathrm {Gr}^d$
, and we use the same notation for the pullbacks to other varieties. For
![]() $d=0$
, or when the index is understood, we omit the superscript. We have canonical isomorphisms
$d=0$
, or when the index is understood, we omit the superscript. We have canonical isomorphisms
where ![]() and
and ![]() as before. (See [Reference AndersonA, Section 3], but note that our sign convention on
as before. (See [Reference AndersonA, Section 3], but note that our sign convention on
![]() $x_i$
is opposite the one used there.)
$x_i$
is opposite the one used there.)
For each fixed point
![]() $w\in \operatorname {\mathrm {Inj}}^0$
, there is a localization homomorphism
$w\in \operatorname {\mathrm {Inj}}^0$
, there is a localization homomorphism ![]() , given by
, given by
 $$\begin{align*}x_i \mapsto y_{w(i)} \qquad \text{and}\qquad c_k \mapsto [t^k]\left(\mathop{\prod_{i\leq0, w(i)>0}}_{j>0,w(j)\leq0} \frac{1+y_{w(j)}t}{1+y_{w(i)}t} \right). \end{align*}$$
$$\begin{align*}x_i \mapsto y_{w(i)} \qquad \text{and}\qquad c_k \mapsto [t^k]\left(\mathop{\prod_{i\leq0, w(i)>0}}_{j>0,w(j)\leq0} \frac{1+y_{w(j)}t}{1+y_{w(i)}t} \right). \end{align*}$$
Here, the operator
![]() $[t^k]$
extracts the coefficient of
$[t^k]$
extracts the coefficient of
![]() $t^k$
, and we always understand
$t^k$
, and we always understand
![]() $y_{a}$
as
$y_{a}$
as
![]() $y_{a \pmod n}$
. Since
$y_{a \pmod n}$
. Since
![]() $w\in \operatorname {\mathrm {Inj}}^0$
, the RHS is a finite product. The same formulas define localization homomorphisms for
$w\in \operatorname {\mathrm {Inj}}^0$
, the RHS is a finite product. The same formulas define localization homomorphisms for
![]() $\mathrm {Gr}$
,
$\mathrm {Gr}$
,
![]() $\widetilde {\mathrm {Fl}}_n$
, and
$\widetilde {\mathrm {Fl}}_n$
, and
![]() $\widetilde {\mathrm {Gr}}_n$
. For
$\widetilde {\mathrm {Gr}}_n$
. For
![]() $\mathrm {Gr}^d$
and
$\mathrm {Gr}^d$
and
![]() $\widetilde {\mathrm {Gr}}^d_n$
with
$\widetilde {\mathrm {Gr}}^d_n$
with
![]() $d\neq 0$
, we use
$d\neq 0$
, we use
 $$\begin{align*}c^{(d)}_k \mapsto [t^k]\left(\mathop{\prod_{i\leq d, w(i)>0}}_{j>d,w(j)\leq0} \frac{1+y_{w(j)}t}{1+y_{w(i)}t} \right). \end{align*}$$
$$\begin{align*}c^{(d)}_k \mapsto [t^k]\left(\mathop{\prod_{i\leq d, w(i)>0}}_{j>d,w(j)\leq0} \frac{1+y_{w(j)}t}{1+y_{w(i)}t} \right). \end{align*}$$
We do not logically require these localization homomorphisms, but they are useful for checking that relations hold, and comparing them against other sources.
The shift morphism determines an automorphism
![]() $\gamma =\operatorname {\mathrm {sh}}^*$
of
$\gamma =\operatorname {\mathrm {sh}}^*$
of
![]() $\Lambda [x,y]$
, by
$\Lambda [x,y]$
, by
where
![]() $C(t) = \sum _{k\geq 0} c_k t^k$
is the generating series for c.
$C(t) = \sum _{k\geq 0} c_k t^k$
is the generating series for c.
The inclusions
![]() $\widetilde {\mathrm {Fl}}_n \hookrightarrow \mathrm {Fl}$
and
$\widetilde {\mathrm {Fl}}_n \hookrightarrow \mathrm {Fl}$
and
![]() $\widetilde {\mathrm {Gr}}_n^d \hookrightarrow \mathrm {Gr}^d$
determine pullback homomorphisms on cohomology: we have maps
$\widetilde {\mathrm {Gr}}_n^d \hookrightarrow \mathrm {Gr}^d$
determine pullback homomorphisms on cohomology: we have maps
The main theorems assert that these homomorphisms are surjective, and specify the kernels. One relation is immediately evident: since
![]() $\operatorname {\mathrm {sh}}^n$
fixes
$\operatorname {\mathrm {sh}}^n$
fixes
![]() $\widetilde {\mathrm {Fl}}_n \subset \mathrm {Fl}$
, we have
$\widetilde {\mathrm {Fl}}_n \subset \mathrm {Fl}$
, we have
![]() $\gamma ^n(c)=c$
, so
$\gamma ^n(c)=c$
, so
 $$\begin{align*}\prod_{i=1}^n \frac{1+y_i t}{1+x_i t} = 1 \end{align*}$$
$$\begin{align*}\prod_{i=1}^n \frac{1+y_i t}{1+x_i t} = 1 \end{align*}$$
in
![]() $H_{{T}}^*\widetilde {\mathrm {Fl}}_n$
. As promised in the introduction, this shows that Corollary B follows from the Theorem.
$H_{{T}}^*\widetilde {\mathrm {Fl}}_n$
. As promised in the introduction, this shows that Corollary B follows from the Theorem.
(An alternative argument uses the fact, not needed here, that the projection
![]() $\widetilde {\mathrm {Fl}}_n \to \widetilde {\mathrm {Gr}}_n$
is topologically identified with the trivial fiber bundle
$\widetilde {\mathrm {Fl}}_n \to \widetilde {\mathrm {Gr}}_n$
is topologically identified with the trivial fiber bundle ![]() .)
.)
2.3 Coproduct
There is a co-commutative coproduct structure on
![]() $\Lambda $
, where the map
$\Lambda $
, where the map
![]() $\Lambda \to \Lambda \otimes \Lambda $
is given by
$\Lambda \to \Lambda \otimes \Lambda $
is given by
![]() $c_k \mapsto c_k \otimes 1 + c_{k-1} \otimes c_1 +\cdots + 1 \otimes c_k$
. This extends
$c_k \mapsto c_k \otimes 1 + c_{k-1} \otimes c_1 +\cdots + 1 \otimes c_k$
. This extends ![]() -linearly to a coproduct on
-linearly to a coproduct on
![]() $\Lambda [y] = H_{{T}}^*\mathrm {Gr}$
. As explained in [Reference AndersonA, Section 8], this can be interpreted as an (equivariant) cohomology pullback via the direct sum morphism
$\Lambda [y] = H_{{T}}^*\mathrm {Gr}$
. As explained in [Reference AndersonA, Section 8], this can be interpreted as an (equivariant) cohomology pullback via the direct sum morphism
![]() $\mathrm {Gr} \times \mathrm {Gr} \to \mathrm {Gr}$
.
$\mathrm {Gr} \times \mathrm {Gr} \to \mathrm {Gr}$
.
Likewise, there is a co-commutative coproduct structure on
![]() $H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
, coming from a homotopy equivalence with the based loop group,
$H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
, coming from a homotopy equivalence with the based loop group,
![]() $\widetilde {\mathrm {Gr}}_n \sim \Omega SU(n)$
(see [Reference Pressley and SegalPS, Section 8.6]). The homotopy equivalence is equivariant with respect to the compact torus
$\widetilde {\mathrm {Gr}}_n \sim \Omega SU(n)$
(see [Reference Pressley and SegalPS, Section 8.6]). The homotopy equivalence is equivariant with respect to the compact torus
![]() $(S^1)^n \subset {T}$
. So the group structure on
$(S^1)^n \subset {T}$
. So the group structure on
![]() $\Omega SU(n)$
determines a coproduct on
$\Omega SU(n)$
determines a coproduct on
![]() $H_{(S^1)^n}^*\Omega SU(n) = H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
. (This coproduct can also be realized algebraically, but the construction is somewhat more involved than the direct sum map for
$H_{(S^1)^n}^*\Omega SU(n) = H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
. (This coproduct can also be realized algebraically, but the construction is somewhat more involved than the direct sum map for
![]() $\mathrm {Gr}$
(see, e.g., [Reference Yun and ZhuYZ]).)
$\mathrm {Gr}$
(see, e.g., [Reference Yun and ZhuYZ]).)
The coproducts on
![]() $H_{T}^*\mathrm {Gr}$
and
$H_{T}^*\mathrm {Gr}$
and
![]() $H_{T}^*\widetilde {\mathrm {Gr}}_n$
are compatible, in the sense that the inclusion
$H_{T}^*\widetilde {\mathrm {Gr}}_n$
are compatible, in the sense that the inclusion
![]() $\widetilde {\mathrm {Gr}}_n \hookrightarrow \mathrm {Gr}$
induces a pullback homomorphism of co-algebras (and in fact, of Hopf algebras): the diagram
$\widetilde {\mathrm {Gr}}_n \hookrightarrow \mathrm {Gr}$
induces a pullback homomorphism of co-algebras (and in fact, of Hopf algebras): the diagram

commutes.
3 Some algebra of symmetric functions
In this section, we introduce some polynomials which appear in the presentations of equivariant cohomology rings, and establish some identities which imply isomorphisms among different such presentations. Most of this comes from basic facts about symmetric functions, and can be found in standard sources (e.g., [Reference MacdonaldMac, Chapter I]). We indicate proofs for facts not easily found there.
Recall ![]() and
and
![]() $\Lambda [y] = \Lambda [y_1,\ldots ,y_n]$
.
$\Lambda [y] = \Lambda [y_1,\ldots ,y_n]$
.
3.1 Some identities in
 $\Lambda [y]$
$\Lambda [y]$
We define elements
![]() $h_k\in \Lambda [y_1,\ldots ,y_n]$
by
$h_k\in \Lambda [y_1,\ldots ,y_n]$
by
 $$ \begin{align} h_k &= \sum_{i=0}^{k-1} \binom{k-1}{i} y_0^i\, c_{k-i}, \end{align} $$
$$ \begin{align} h_k &= \sum_{i=0}^{k-1} \binom{k-1}{i} y_0^i\, c_{k-i}, \end{align} $$
writing
![]() $y_0=y_n$
to emphasize stability with respect to n.
$y_0=y_n$
to emphasize stability with respect to n.
Let
![]() $H(t)=\sum _{k\geq 0} h_k t^k$
and
$H(t)=\sum _{k\geq 0} h_k t^k$
and
![]() $C(t) = \sum _{k\geq 0} c_k t^k$
be the generating series, with
$C(t) = \sum _{k\geq 0} c_k t^k$
be the generating series, with
![]() ${h_0=c_0=1}$
. Then (3.1) is equivalent to
${h_0=c_0=1}$
. Then (3.1) is equivalent to
![]() $H(t) = C\left ( t/(1-y_0t) \right )$
. Both the h’s and the c’s are algebraically independent generators of
$H(t) = C\left ( t/(1-y_0t) \right )$
. Both the h’s and the c’s are algebraically independent generators of
![]() $\Lambda [y]$
as a
$\Lambda [y]$
as a ![]() -algebra.
-algebra.
We have the elements ![]() given by
given by
 $$ \begin{align} P(t) := \sum_{k\geq 1} p_k t^{k-1} = \frac{d}{dt}\log C(t). \end{align} $$
$$ \begin{align} P(t) := \sum_{k\geq 1} p_k t^{k-1} = \frac{d}{dt}\log C(t). \end{align} $$
We define new elements ![]() by the analogous identity of generating series:
by the analogous identity of generating series:
 $$ \begin{align} \widetilde{P}(t) := \sum_{k\geq 1} \widetilde{p}_k t^{k-1} = \frac{d}{dt}\log H(t). \end{align} $$
$$ \begin{align} \widetilde{P}(t) := \sum_{k\geq 1} \widetilde{p}_k t^{k-1} = \frac{d}{dt}\log H(t). \end{align} $$
(These formulas are equivalent to the Newton relations (1.1) (see, e.g., [Reference MacdonaldMac, Section 2]).)
Let
![]() $E(t) = \prod _{i=1}^n (1+ y_i t)$
be the generating series for the elementary symmetric polynomials in
$E(t) = \prod _{i=1}^n (1+ y_i t)$
be the generating series for the elementary symmetric polynomials in
![]() $y_1,\ldots ,y_n$
, and let
$y_1,\ldots ,y_n$
, and let
![]() $\widetilde {E}(t) = \prod _{i=1}^n (1+(y_i-y_0)t)$
be the corresponding series in variables
$\widetilde {E}(t) = \prod _{i=1}^n (1+(y_i-y_0)t)$
be the corresponding series in variables
![]() $y_i-y_0$
. So
$y_i-y_0$
. So
![]() $\widetilde {E}(t) = E(t/(1-y_0t))\cdot (1-y_0t)^n$
.
$\widetilde {E}(t) = E(t/(1-y_0t))\cdot (1-y_0t)^n$
.
Finally, let
and
Equivalently, the generating series for
![]() $p_k(c|y)$
and
$p_k(c|y)$
and
![]() $\widetilde {p}_k(h|y)$
are given by
$\widetilde {p}_k(h|y)$
are given by
respectively.
The polynomials
![]() $p_k(c|y)$
are those appearing in the main theorem from the introduction. The variations
$p_k(c|y)$
are those appearing in the main theorem from the introduction. The variations
![]() $\widetilde {p}_k(h|y)$
will be easier to interpret as relations in the equivariant cohomology ring of the affine Grassmannian (in Section 4). We wish to compare the ideals generated by
$\widetilde {p}_k(h|y)$
will be easier to interpret as relations in the equivariant cohomology ring of the affine Grassmannian (in Section 4). We wish to compare the ideals generated by
![]() $p_k(c|y)$
and
$p_k(c|y)$
and
![]() $\widetilde {p}_k(h|y)$
.
$\widetilde {p}_k(h|y)$
.
Lemma 3.1 For
![]() $k\geq n$
, we have
$k\geq n$
, we have
 $$ \begin{align} \widetilde{p}_k(h|y) = \sum_{i=0}^{k-1} \binom{k-n}{i} y_0^i p_{k-i}(c|y) \end{align} $$
$$ \begin{align} \widetilde{p}_k(h|y) = \sum_{i=0}^{k-1} \binom{k-n}{i} y_0^i p_{k-i}(c|y) \end{align} $$
and
 $$ \begin{align} p_k(c|y) = \sum_{i=0}^{k-1} \binom{k-n}{i} (-y_0)^i \widetilde{p}_{k-i}(h|y). \end{align} $$
$$ \begin{align} p_k(c|y) = \sum_{i=0}^{k-1} \binom{k-n}{i} (-y_0)^i \widetilde{p}_{k-i}(h|y). \end{align} $$
In particular, we have an equality
of ideals in
![]() $\Lambda [y_1,\ldots ,y_n]$
.
$\Lambda [y_1,\ldots ,y_n]$
.
Proof The second statement follows from the first, the RHS of (3.6) involves only
![]() $p_i(c|y)$
for
$p_i(c|y)$
for
![]() $i\geq n$
, and likewise the RHS of (3.7) involves only
$i\geq n$
, and likewise the RHS of (3.7) involves only
![]() $\widetilde {p}_i(h|y)$
for
$\widetilde {p}_i(h|y)$
for
![]() $i\geq n$
.
$i\geq n$
.
To prove (3.6), we expand the definitions and compute
 $$ \begin{align*} \widetilde{\boldsymbol{P}}(t) &= \widetilde{P}(t)\cdot \widetilde{E}(t) \\ &= \left(\frac{d}{dt}\log H(t)\right)\cdot E\Big( t/(1-y_0t) \Big)\cdot (1-y_0t)^n \\ &= \left(\frac{d}{dt}\log C\Big( t/(1-y_0t) \Big)\right)\cdot E\Big( t/(1-y_0t) \Big)\cdot (1-y_0t)^n \\ &= \frac{1}{(1-y_0t)^2} P\Big( t/(1-y_0t) \Big) \cdot E\Big( t/(1-y_0t) \Big)\cdot (1-y_0t)^n \\ &= (1-y_0t)^{n-2}\boldsymbol{P}\Big( t/(1-y_0t) \Big). \end{align*} $$
$$ \begin{align*} \widetilde{\boldsymbol{P}}(t) &= \widetilde{P}(t)\cdot \widetilde{E}(t) \\ &= \left(\frac{d}{dt}\log H(t)\right)\cdot E\Big( t/(1-y_0t) \Big)\cdot (1-y_0t)^n \\ &= \left(\frac{d}{dt}\log C\Big( t/(1-y_0t) \Big)\right)\cdot E\Big( t/(1-y_0t) \Big)\cdot (1-y_0t)^n \\ &= \frac{1}{(1-y_0t)^2} P\Big( t/(1-y_0t) \Big) \cdot E\Big( t/(1-y_0t) \Big)\cdot (1-y_0t)^n \\ &= (1-y_0t)^{n-2}\boldsymbol{P}\Big( t/(1-y_0t) \Big). \end{align*} $$
Expanding the RHS, we obtain
 $$\begin{align*}\sum_{m\geq 1} p_m(c|y) t^{m-1} (1-y_0 t)^{n-m-1} = \mathop{\sum_{m\geq 1}}_{i\geq 0} p_m(c|y) \binom{n-m-1}{i}(-y_0)^i t^{m-1+i}. \end{align*}$$
$$\begin{align*}\sum_{m\geq 1} p_m(c|y) t^{m-1} (1-y_0 t)^{n-m-1} = \mathop{\sum_{m\geq 1}}_{i\geq 0} p_m(c|y) \binom{n-m-1}{i}(-y_0)^i t^{m-1+i}. \end{align*}$$
Setting
![]() $k=m+i$
, for
$k=m+i$
, for
![]() $k\geq n$
, the coefficient of
$k\geq n$
, the coefficient of
![]() $t^{k-1}$
is
$t^{k-1}$
is
 $$\begin{align*}\sum_{i=0}^{k-1} \binom{n-k+i-1}{i}(-y_0)^i p_{k-i}(c|y) = \sum_{i=0}^{k-1} \binom{k-n}{i}y_0^i p_{k-i}(c|y), \end{align*}$$
$$\begin{align*}\sum_{i=0}^{k-1} \binom{n-k+i-1}{i}(-y_0)^i p_{k-i}(c|y) = \sum_{i=0}^{k-1} \binom{k-n}{i}y_0^i p_{k-i}(c|y), \end{align*}$$
as desired. (The last equality uses the extended binomial coefficient identity
![]() $\binom {-m}{i} = (-1)^i\binom {m+i-1}{i}$
.) The proof of (3.7) is analogous.
$\binom {-m}{i} = (-1)^i\binom {m+i-1}{i}$
.) The proof of (3.7) is analogous.
3.2 Notation for symmetric functions in
 $\xi $
$\xi $
Let ![]() be the ring of symmetric functions in countably many variables
be the ring of symmetric functions in countably many variables
![]() $\xi _1,\xi _2,\ldots $
, each of degree
$\xi _1,\xi _2,\ldots $
, each of degree
![]() $2$
. This is the inverse limit of
$2$
. This is the inverse limit of ![]() as
as
![]() $r\to \infty $
(in the category of graded rings). It may be identified with the polynomial ring
$r\to \infty $
(in the category of graded rings). It may be identified with the polynomial ring ![]() , where
, where
![]() $h_k(\xi )$
is the complete homogeneous symmetric function in
$h_k(\xi )$
is the complete homogeneous symmetric function in
![]() $\xi $
.
$\xi $
.
There is also a ![]() -linear basis for
-linear basis for
![]() $\Lambda ^{(\xi )}$
consisting of the monomial symmetric functions
$\Lambda ^{(\xi )}$
consisting of the monomial symmetric functions
![]() $m_\lambda (\xi )$
. Given a partition
$m_\lambda (\xi )$
. Given a partition
![]() $\lambda = (\lambda _1 \geq \lambda _2 \geq \cdots \geq \lambda _r\geq 0)$
, the function
$\lambda = (\lambda _1 \geq \lambda _2 \geq \cdots \geq \lambda _r\geq 0)$
, the function
![]() $m_\lambda (\xi )$
is the symmetrization of the monomial
$m_\lambda (\xi )$
is the symmetrization of the monomial
![]() $\xi _1^{\lambda _1} \xi _2^{\lambda _2} \cdots \xi _r^{\lambda _r}$
– that is, the sum of all distinct permutations of this monomial.
$\xi _1^{\lambda _1} \xi _2^{\lambda _2} \cdots \xi _r^{\lambda _r}$
– that is, the sum of all distinct permutations of this monomial.
The power sum functions
![]() $p_k(\xi ) = \xi _1^k + \xi _2^k + \cdots $
also play an important role. They generate
$p_k(\xi ) = \xi _1^k + \xi _2^k + \cdots $
also play an important role. They generate
![]() $\Lambda ^{(\xi )}$
as a
$\Lambda ^{(\xi )}$
as a ![]() -algebra, but not as a
-algebra, but not as a ![]() -algebra. The function
-algebra. The function
![]() $p_k(\xi )$
is expressed in terms of the functions
$p_k(\xi )$
is expressed in terms of the functions
![]() $h_k(\xi )$
via the Newton relations, which can be written as the determinant (1.1), substituting
$h_k(\xi )$
via the Newton relations, which can be written as the determinant (1.1), substituting
![]() $h_k(\xi )$
for
$h_k(\xi )$
for
![]() $c_k$
in the matrix.
$c_k$
in the matrix.
There is an isomorphism ![]() determined by evaluating the generating series
determined by evaluating the generating series
![]() $C(t) = \sum c_k t^k$
as
$C(t) = \sum c_k t^k$
as
Under this identification, we have
![]() $H(t) = \prod _{i\geq 1} \frac {1}{1-\xi _i t}$
, so
$H(t) = \prod _{i\geq 1} \frac {1}{1-\xi _i t}$
, so
![]() $h_k$
maps to
$h_k$
maps to
![]() $h_k(\xi )$
, and it follows that
$h_k(\xi )$
, and it follows that
![]() $\widetilde {p}_k$
maps to the power sum function
$\widetilde {p}_k$
maps to the power sum function
![]() $p_k(\xi )$
. In what follows, we will sometimes use this identification without further comment.
$p_k(\xi )$
. In what follows, we will sometimes use this identification without further comment.
3.3 Another equality of ideals
In Section 4, we require another algebraic lemma. First, we consider finitely many variables
![]() $\xi _1,\ldots ,\xi _r$
, and the symmetric polynomial ring
$\xi _1,\ldots ,\xi _r$
, and the symmetric polynomial ring ![]() .
.
Lemma 3.2 Fix
![]() $n>0$
, and consider the ideal
$n>0$
, and consider the ideal ![]() . As ideals in
. As ideals in
![]() $\Lambda ^{(\xi )}$
, we have
$\Lambda ^{(\xi )}$
, we have
Proof The first equality holds because monomials
![]() $\xi _1^{a_1}\cdots \xi _r^{a_r}$
with some
$\xi _1^{a_1}\cdots \xi _r^{a_r}$
with some
![]() $a_i\geq n$
form a
$a_i\geq n$
form a ![]() -linear basis for
-linear basis for ![]() . For the second equality, the inclusion “
. For the second equality, the inclusion “
![]() $\supseteq $
” is evident, because
$\supseteq $
” is evident, because
![]() $p_k = m_{(k)}$
. It remains to see that
$p_k = m_{(k)}$
. It remains to see that
![]() $m_\lambda $
lies in the ideal
$m_\lambda $
lies in the ideal
![]() $(p_k)_{k\geq n}$
whenever
$(p_k)_{k\geq n}$
whenever
![]() $\lambda _1\geq n$
, and this is proved by induction on the number of parts of
$\lambda _1\geq n$
, and this is proved by induction on the number of parts of
![]() $\lambda $
.
$\lambda $
.
Taking the inverse limit over r (in the category of graded rings), we obtain the following:
Corollary 3.3 We have isomorphisms of graded rings

4 Proof of the main theorem
Given any variety X with basepoint
![]() $p_0$
, Bott [Reference BottBo] considers a system of embeddings
$p_0$
, Bott [Reference BottBo] considers a system of embeddings
Assume
![]() ${T}$
acts on X, fixing
${T}$
acts on X, fixing
![]() $p_0$
, so these embeddings are
$p_0$
, so these embeddings are
![]() ${T}$
-equivariant. The symmetric group
${T}$
-equivariant. The symmetric group
![]() $\mathcal {S}_r$
acts on these products by permuting factors, and therefore on their (equivariant) cohomology rings. The inverse limit is written
$\mathcal {S}_r$
acts on these products by permuting factors, and therefore on their (equivariant) cohomology rings. The inverse limit is written
We further assume
![]() $H_{T}^*X$
is free over
$H_{T}^*X$
is free over ![]() , and has no odd cohomology. Then
, and has no odd cohomology. Then ![]() (r factors). In this case, given any
(r factors). In this case, given any
![]() ${T}$
-equivariant morphism
${T}$
-equivariant morphism
![]() $f\colon X \to \widetilde {\mathrm {Gr}}_n$
, there is a pullback homomorphism
$f\colon X \to \widetilde {\mathrm {Gr}}_n$
, there is a pullback homomorphism
obtained by factoring through the r-fold coproduct on
![]() $H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
. Since the coproduct is commutative, the image lies in the
$H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
. Since the coproduct is commutative, the image lies in the
![]() $\mathcal {S}_r$
-invariant part of the tensor product. Taking the limit over r produces a homomorphism
$\mathcal {S}_r$
-invariant part of the tensor product. Taking the limit over r produces a homomorphism
For X, we take projective space ![]() , with basepoint
, with basepoint
![]() $p_0$
corresponding to the line
$p_0$
corresponding to the line ![]() , which is scaled by the character
, which is scaled by the character
![]() $y_0=y_n$
. (Recall that we treat indices of
$y_0=y_n$
. (Recall that we treat indices of
![]() $y_i$
modulo n.)
$y_i$
modulo n.)
Let ![]() be the hyperplane defined by
be the hyperplane defined by
![]() $e^*_0=0$
, and let
$e^*_0=0$
, and let
![]() $\xi = [H]$
be its class in
$\xi = [H]$
be its class in ![]() . So
. So
![]() $\xi =c_1^{T}(\mathcal {O}(1)) + y_0$
, where
$\xi =c_1^{T}(\mathcal {O}(1)) + y_0$
, where
![]() $\mathcal {O}(1)$
is the dual of the tautological bundle on
$\mathcal {O}(1)$
is the dual of the tautological bundle on ![]() . The equivariant cohomology ring of
. The equivariant cohomology ring of ![]() has a well-known presentation, which in our notation takes the form
has a well-known presentation, which in our notation takes the form
Written slightly differently, the defining relation is
 $$ \begin{align} \xi^n + \xi^{n-1}\, e_1(y_1-y_0,\ldots,y_n-y_0) + \cdots \\ \qquad + \xi\, e_{n-1}(y_1-y_0,\ldots,y_n-y_0) = 0, \nonumber \end{align} $$
$$ \begin{align} \xi^n + \xi^{n-1}\, e_1(y_1-y_0,\ldots,y_n-y_0) + \cdots \\ \qquad + \xi\, e_{n-1}(y_1-y_0,\ldots,y_n-y_0) = 0, \nonumber \end{align} $$
which one should compare with (3.5). Similarly, let ![]() be the hyperplane defined by
be the hyperplane defined by
![]() $e^*_0=0$
on the
$e^*_0=0$
on the
![]() $i\mathrm {th}$
factor, and let
$i\mathrm {th}$
factor, and let
![]() $\xi _i = [H_i]$
be its class in
$\xi _i = [H_i]$
be its class in ![]() , which has a presentation with one relation of the form (4.3) for each
, which has a presentation with one relation of the form (4.3) for each
![]() $\xi _i$
. Taking symmetric invariants leads to the following calculation:
$\xi _i$
. Taking symmetric invariants leads to the following calculation:
Lemma 4.1 The ring ![]() is a free
is a free ![]() -algebra. Letting
-algebra. Letting
![]() $\widetilde {p}_k(\xi |y)$
be the polynomials defined by (3.5), where
$\widetilde {p}_k(\xi |y)$
be the polynomials defined by (3.5), where
![]() $\widetilde {p}_k=p_k(\xi )=\xi _1^k+\xi _2^k+\cdots $
, it has the presentation
$\widetilde {p}_k=p_k(\xi )=\xi _1^k+\xi _2^k+\cdots $
, it has the presentation
Proof The homomorphism ![]() is the limit of homomorphisms
is the limit of homomorphisms ![]() defined by
defined by
![]() $\xi _i\mapsto [H_i]$
. The relations
$\xi _i\mapsto [H_i]$
. The relations
![]() $\widetilde {p}_k(\xi |y)=0$
hold in
$\widetilde {p}_k(\xi |y)=0$
hold in ![]() , because they symmetrize relations of the form (4.3), so there is a well-defined homomorphism modulo the ideal
, because they symmetrize relations of the form (4.3), so there is a well-defined homomorphism modulo the ideal
![]() $\big ( \widetilde {p}_k(\xi |y) \big )_{k\geq n}$
. Modulo the y-variables, this reduces to the isomorphism described in Corollary 3.3. The assertion follows by graded Nakayama.
$\big ( \widetilde {p}_k(\xi |y) \big )_{k\geq n}$
. Modulo the y-variables, this reduces to the isomorphism described in Corollary 3.3. The assertion follows by graded Nakayama.
One embeds ![]() in
in
![]() $\mathrm {Gr}$
by sending
$\mathrm {Gr}$
by sending
![]() $L \subset V_{[0,n-1]}$
to
$L \subset V_{[0,n-1]}$
to
![]() $V_{<0}\oplus L \subset V$
, and this embedding factors through
$V_{<0}\oplus L \subset V$
, and this embedding factors through
![]() $\widetilde {\mathrm {Gr}}_n$
, all
$\widetilde {\mathrm {Gr}}_n$
, all
![]() ${T}$
-equivariantly. So we have homomorphisms
${T}$
-equivariantly. So we have homomorphisms
The map ![]() sends the generating series
sends the generating series
The map ![]() is determined by the evaluation (3.8).
is determined by the evaluation (3.8).
Proposition 4.2 The homomorphism ![]() is an isomorphism of
is an isomorphism of ![]() -algebras. In particular, we have
-algebras. In particular, we have
Proof The affine Grassmannian has a
![]() ${T}$
-invariant Schubert cell decomposition, with finitely many cells in each dimension, so
${T}$
-invariant Schubert cell decomposition, with finitely many cells in each dimension, so
![]() $H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
is a free
$H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
is a free ![]() -module. It follows that the non-equivariant cohomology is recovered by setting y-variables to
-module. It follows that the non-equivariant cohomology is recovered by setting y-variables to
![]() $0$
: we have an isomorphism
$0$
: we have an isomorphism
![]() $(H_{{T}}^*\widetilde {\mathrm {Gr}}_n)/(y) \cong H^*\widetilde {\mathrm {Gr}}_n$
, and likewise
$(H_{{T}}^*\widetilde {\mathrm {Gr}}_n)/(y) \cong H^*\widetilde {\mathrm {Gr}}_n$
, and likewise ![]() . The induced map
. The induced map ![]() was shown to be an isomorphism by Bott [Reference BottBo, Proposition 8.1]. So the first statement of the proposition follows by another application of graded Nakayama. The second statement is a combination of the first with the presentation of
was shown to be an isomorphism by Bott [Reference BottBo, Proposition 8.1]. So the first statement of the proposition follows by another application of graded Nakayama. The second statement is a combination of the first with the presentation of ![]() from Lemma 4.1.
from Lemma 4.1.
The
![]() $d=0$
case of the main theorem follows from Proposition 4.2 together with the equality of ideals
$d=0$
case of the main theorem follows from Proposition 4.2 together with the equality of ideals
![]() $\big ( \widetilde {p}_k(h|y) \big )_{k\geq n} = \big ( p_k(c|y) \big )_{k\geq n}$
established in Lemma 3.1.
$\big ( \widetilde {p}_k(h|y) \big )_{k\geq n} = \big ( p_k(c|y) \big )_{k\geq n}$
established in Lemma 3.1.
For the general d case, we use the shift morphism
![]() $\operatorname {\mathrm {sh}}^d$
, which defines isomorphisms
$\operatorname {\mathrm {sh}}^d$
, which defines isomorphisms

These are equivariant with respect to the corresponding automorphism of
![]() ${T}$
which cyclically permutes coordinates. The action on cohomology rings is given by the homomorphism
${T}$
which cyclically permutes coordinates. The action on cohomology rings is given by the homomorphism
![]() $\gamma ^d$
, as described in Section 2.2. The presentation of
$\gamma ^d$
, as described in Section 2.2. The presentation of
![]() $H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
is mapped to
$H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
is mapped to
where now ![]() , and the variables map by
, and the variables map by ![]() . It remains to express
. It remains to express
![]() $\gamma ^d p_k(c|y)$
in terms of the polynomials
$\gamma ^d p_k(c|y)$
in terms of the polynomials
![]() $p_k(c^{(d)}|y)$
.
$p_k(c^{(d)}|y)$
.
Since ![]() , we have
, we have
where
![]() $C^{(d)}(t) = \sum _{k\geq 0} c_k^{(d)} t^k$
is the generating series. So, using notation from Section 3, we have
$C^{(d)}(t) = \sum _{k\geq 0} c_k^{(d)} t^k$
is the generating series. So, using notation from Section 3, we have
 $$ \begin{align*} \gamma^d\boldsymbol{P}(t) &= \big(\gamma^d P(t) \big)\cdot \big(\gamma^d E(t) \big) \\ &= \left( \frac{d}{dt}\log \gamma^d C(t) \right) \cdot E(t) \\ &= \frac{d}{dt}\log \left( C^{(d)}(t)\prod_{i=1}^d (1+y_i t) \right) \cdot E(t) \\ &= P^{(d)}(t) \cdot E(t) + \sum_{i=1}^d y_i (1+y_1 t) \cdots \widehat{(1+y_i t)} \cdots (1+y_n t), \end{align*} $$
$$ \begin{align*} \gamma^d\boldsymbol{P}(t) &= \big(\gamma^d P(t) \big)\cdot \big(\gamma^d E(t) \big) \\ &= \left( \frac{d}{dt}\log \gamma^d C(t) \right) \cdot E(t) \\ &= \frac{d}{dt}\log \left( C^{(d)}(t)\prod_{i=1}^d (1+y_i t) \right) \cdot E(t) \\ &= P^{(d)}(t) \cdot E(t) + \sum_{i=1}^d y_i (1+y_1 t) \cdots \widehat{(1+y_i t)} \cdots (1+y_n t), \end{align*} $$
where
![]() $P^{(d)}(t) = \sum _{k\geq 1} p_k(c^{(d)}|y) t^{k-1}$
. Extracting the coefficients of
$P^{(d)}(t) = \sum _{k\geq 1} p_k(c^{(d)}|y) t^{k-1}$
. Extracting the coefficients of
![]() $t^{k-1}$
, we find
$t^{k-1}$
, we find
and
for
![]() $k>n$
, as claimed.
$k>n$
, as claimed.
Remark 4.3 Consider the ![]() -algebra automorphism of
-algebra automorphism of
![]() $\Lambda [y]$
defined by sending
$\Lambda [y]$
defined by sending
![]() $p_k(c)$
to
$p_k(c)$
to
![]() $p_k(c) - (-1)^k p_k(y)$
, where
$p_k(c) - (-1)^k p_k(y)$
, where
![]() $p_k(y) = y_1^k+\cdots +y_n^k$
. Using [Reference MacdonaldMac, (2.11’)], this sends
$p_k(y) = y_1^k+\cdots +y_n^k$
. Using [Reference MacdonaldMac, (2.11’)], this sends
So we have an isomorphism of ![]() -algebras
-algebras
![]() $\Lambda [y]/I_n^d \xrightarrow {\sim } \Lambda [y]/I_n^{d+n}$
.
$\Lambda [y]/I_n^d \xrightarrow {\sim } \Lambda [y]/I_n^{d+n}$
.
5 Double monomial symmetric functions
The monomial symmetric functions
![]() $m_\lambda (\xi )$
, with
$m_\lambda (\xi )$
, with
![]() $\lambda _1<n$
, form a basis for
$\lambda _1<n$
, form a basis for ![]() over
over ![]() – so they also form a basis for
– so they also form a basis for
![]() $H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
. (This follows from the arguments above, and it is also easy to see directly from the fact that
$H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
. (This follows from the arguments above, and it is also easy to see directly from the fact that
![]() $1,\xi ,\ldots ,\xi ^{n-1}$
forms a basis for
$1,\xi ,\ldots ,\xi ^{n-1}$
forms a basis for ![]() over
over ![]() .) It is useful to work with a deformation of this basis of
.) It is useful to work with a deformation of this basis of
![]() $\Lambda [y]$
, which extends a basis for the defining ideal of
$\Lambda [y]$
, which extends a basis for the defining ideal of
![]() $H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
.
$H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
.
For the general definition, we use variables
![]() $a_1,a_2,\ldots $
in degree
$a_1,a_2,\ldots $
in degree
![]() $2$
. Given a sequence
$2$
. Given a sequence
![]() $\alpha =(\alpha _1,\ldots ,\alpha _r)$
of positive integers, let
$\alpha =(\alpha _1,\ldots ,\alpha _r)$
of positive integers, let
![]() $n_i(\alpha )$
be the number of occurrences of i in
$n_i(\alpha )$
be the number of occurrences of i in
![]() $\alpha $
, and set
$\alpha $
, and set
![]() $n(\alpha ) := n_1(\alpha )! n_2(\alpha )!\cdots $
. (So
$n(\alpha ) := n_1(\alpha )! n_2(\alpha )!\cdots $
. (So
![]() $n(\alpha )$
is the number of permutations fixing
$n(\alpha )$
is the number of permutations fixing
![]() $\alpha $
.) For a partition
$\alpha $
.) For a partition
![]() $\lambda $
with r parts, so
$\lambda $
with r parts, so
![]() $\lambda =(\lambda _1\geq \cdots \geq \lambda _r>0)$
, we write
$\lambda =(\lambda _1\geq \cdots \geq \lambda _r>0)$
, we write
![]() $\alpha \subset \lambda $
to mean
$\alpha \subset \lambda $
to mean
![]() $\alpha _i\leq \lambda _i$
for all i. Let
$\alpha _i\leq \lambda _i$
for all i. Let
where
![]() $e_k$
is the elementary symmetric polynomial.
$e_k$
is the elementary symmetric polynomial.
Definition 5.1 The double monomial symmetric function is
 $$\begin{align*}m_\lambda(\xi|a) = \sum_{(1^r) \subset \alpha \subset \lambda} \frac{n(\alpha)}{n(\lambda)} e_{\lambda-\alpha}(a)\, m_\alpha(\xi), \end{align*}$$
$$\begin{align*}m_\lambda(\xi|a) = \sum_{(1^r) \subset \alpha \subset \lambda} \frac{n(\alpha)}{n(\lambda)} e_{\lambda-\alpha}(a)\, m_\alpha(\xi), \end{align*}$$
an element of
![]() $\Lambda ^{(\xi )}[a_1,a_2,\ldots ]$
.
$\Lambda ^{(\xi )}[a_1,a_2,\ldots ]$
.
For a given
![]() $\alpha $
, the coefficient
$\alpha $
, the coefficient
![]() $n(\alpha )/n(\lambda )$
need not be an integer, but in the sum over all
$n(\alpha )/n(\lambda )$
need not be an integer, but in the sum over all
![]() $\alpha $
, the coefficients are integers. In fact,
$\alpha $
, the coefficients are integers. In fact,
![]() $m_\lambda (\xi |a)$
is the symmetrization of the “monomial”
$m_\lambda (\xi |a)$
is the symmetrization of the “monomial”
 $$ \begin{align} (\xi|a)^\lambda &= \prod_{i=1}^r \xi_i(\xi_i+a_1)\cdots(\xi_i+a_{\lambda_i-1}) \\ &= \sum_{(1^r)\subset \alpha \subset \lambda} e_{\lambda-\alpha}(a)\, \xi^\alpha, \nonumber \end{align} $$
$$ \begin{align} (\xi|a)^\lambda &= \prod_{i=1}^r \xi_i(\xi_i+a_1)\cdots(\xi_i+a_{\lambda_i-1}) \\ &= \sum_{(1^r)\subset \alpha \subset \lambda} e_{\lambda-\alpha}(a)\, \xi^\alpha, \nonumber \end{align} $$
i.e., it is the sum of
![]() $\sigma \big ((\xi |a)^{\lambda }\big )$
over all distinct permutations
$\sigma \big ((\xi |a)^{\lambda }\big )$
over all distinct permutations
![]() $\sigma $
of
$\sigma $
of
![]() $\lambda $
, where
$\lambda $
, where
![]() $\sigma $
acts in the usual way by permuting the
$\sigma $
acts in the usual way by permuting the
![]() $\xi $
variables.
$\xi $
variables.
For instance, the functions corresponding to
![]() $\lambda $
with a single row are
$\lambda $
with a single row are
Other examples are
 $$ \begin{align*} m_{21}(\xi|a) &= m_{21}(\xi) + 2a_1\,m_{11}(\xi), \\ m_{22}(\xi|a) &= m_{22}(\xi) + a_1\, m_{21}(\xi) + a_1^2\, m_{11}(\xi), \\ m_{31}(\xi|a) &= m_{31}(\xi) + (a_1+a_2)\, m_{21}(\xi) + 2 a_1 a_2\, m_{11}(\xi), \\ m_{32}(\xi|a) &= m_{32}(\xi) + 2(a_1+a_2)\, m_{22}(\xi) + a_1\, m_{31}(\xi) \\ & \qquad + a_1 (a_1+2a_2)\, m_{21}+ 2 a_1^2 a_2\, m_{11}(\xi). \end{align*} $$
$$ \begin{align*} m_{21}(\xi|a) &= m_{21}(\xi) + 2a_1\,m_{11}(\xi), \\ m_{22}(\xi|a) &= m_{22}(\xi) + a_1\, m_{21}(\xi) + a_1^2\, m_{11}(\xi), \\ m_{31}(\xi|a) &= m_{31}(\xi) + (a_1+a_2)\, m_{21}(\xi) + 2 a_1 a_2\, m_{11}(\xi), \\ m_{32}(\xi|a) &= m_{32}(\xi) + 2(a_1+a_2)\, m_{22}(\xi) + a_1\, m_{31}(\xi) \\ & \qquad + a_1 (a_1+2a_2)\, m_{21}+ 2 a_1^2 a_2\, m_{11}(\xi). \end{align*} $$
From now on, we evaluate the a variables as
![]() $a_i=y_i-y_0$
, with the indices taken mod n as usual. In the single-row case, this recovers the double power sum function defined by (3.5) in Section 3 above:
$a_i=y_i-y_0$
, with the indices taken mod n as usual. In the single-row case, this recovers the double power sum function defined by (3.5) in Section 3 above:
![]() $m_k(\xi |a)=\widetilde {p}_k(\xi |y)$
.
$m_k(\xi |a)=\widetilde {p}_k(\xi |y)$
.
We use the isomorphism
![]() $\Lambda ^{(\xi )}[y] \cong \Lambda [y]$
from (3.8) to identify the functions
$\Lambda ^{(\xi )}[y] \cong \Lambda [y]$
from (3.8) to identify the functions
![]() $m_\lambda (\xi |y)$
in
$m_\lambda (\xi |y)$
in
![]() $\Lambda ^{(\xi )}[y]$
with elements
$\Lambda ^{(\xi )}[y]$
with elements
![]() $m_\lambda (c|y)$
in
$m_\lambda (c|y)$
in
![]() $\Lambda [y]$
, also called double monomial functions.
$\Lambda [y]$
, also called double monomial functions.
Proposition 5.2 The double monomial functions
![]() $m_\lambda (c|y)$
form a
$m_\lambda (c|y)$
form a ![]() -linear basis for
-linear basis for
![]() $\Lambda [y]$
. The
$\Lambda [y]$
. The
![]() $m_\lambda (c|y)$
with
$m_\lambda (c|y)$
with
![]() $\lambda _1\geq n$
form a
$\lambda _1\geq n$
form a ![]() -linear basis for the ideal
-linear basis for the ideal
![]() $I_n \subset \Lambda [y]$
, the kernel of the surjective homomorphism
$I_n \subset \Lambda [y]$
, the kernel of the surjective homomorphism
![]() $\Lambda [y]=H_{{T}}^*\mathrm {Gr} \to H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
.
$\Lambda [y]=H_{{T}}^*\mathrm {Gr} \to H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
.
The ideal here is
![]() $I_n=I_n^0$
, in the notation of the main Theorem from the introduction. In particular, Proposition 5.2 implies that every class in
$I_n=I_n^0$
, in the notation of the main Theorem from the introduction. In particular, Proposition 5.2 implies that every class in
![]() $H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
has a canonical lift to a polynomial in
$H_{{T}}^*\widetilde {\mathrm {Gr}}_n$
has a canonical lift to a polynomial in
![]() $\Lambda [y]$
, by taking an expansion in the monomial basis as a normal form, using only those
$\Lambda [y]$
, by taking an expansion in the monomial basis as a normal form, using only those
![]() $m_\lambda (c|y)$
with
$m_\lambda (c|y)$
with
![]() $\lambda _1<n$
.
$\lambda _1<n$
.
Proof The first statement is proved by setting
![]() $y=0$
, since the monomial functions
$y=0$
, since the monomial functions
![]() $m_\lambda $
form a basis for
$m_\lambda $
form a basis for
![]() $\Lambda $
. For the second statement, it suffices to check that each
$\Lambda $
. For the second statement, it suffices to check that each
![]() $m_\lambda (c|y)$
lies in the ideal. This follows from the characterization of
$m_\lambda (c|y)$
lies in the ideal. This follows from the characterization of
![]() $m_\lambda (\xi |a)$
as the symmetrization of the monomial
$m_\lambda (\xi |a)$
as the symmetrization of the monomial
![]() $(\xi |a)^\lambda $
defined in (5.1). Indeed, after setting
$(\xi |a)^\lambda $
defined in (5.1). Indeed, after setting
![]() $\xi _i = [H_i]$
and
$\xi _i = [H_i]$
and
![]() $a_i = y_i-y_0$
, as in Section 4, each
$a_i = y_i-y_0$
, as in Section 4, each
![]() $(\xi |a)^\lambda $
with
$(\xi |a)^\lambda $
with
![]() $\lambda _1\geq n$
lies in the ideal defining
$\lambda _1\geq n$
lies in the ideal defining ![]() , so the symmetrization lies in the defining ideal of
, so the symmetrization lies in the defining ideal of ![]() .
.
Remark 5.3 Up to sign and reindexing variables, the single-row functions
![]() $m_{k}(\xi |a)$
nearly agree with the functions
$m_{k}(\xi |a)$
nearly agree with the functions
![]() $\widetilde {m}_k(x|\!|a)$
in [Reference Lam and ShimozonoLS, Section 4.5]. To make the identification, use an isomorphism of our
$\widetilde {m}_k(x|\!|a)$
in [Reference Lam and ShimozonoLS, Section 4.5]. To make the identification, use an isomorphism of our
![]() $\Lambda ^{(\xi )}[a]$
with their
$\Lambda ^{(\xi )}[a]$
with their
![]() $\Lambda (x|\!|a)$
which sends
$\Lambda (x|\!|a)$
which sends
![]() $m_k(\xi ) \mapsto m_k[x-a_{>0}]$
and
$m_k(\xi ) \mapsto m_k[x-a_{>0}]$
and
![]() $a_i \mapsto -a_{1-i}$
. Then the image of our
$a_i \mapsto -a_{1-i}$
. Then the image of our
![]() $m_k(\xi |a)$
is the result of setting
$m_k(\xi |a)$
is the result of setting
![]() $a_1=0$
in
$a_1=0$
in
![]() $\widetilde {m}_k(x|\!|a)$
. In general, however, the double monomial functions defined here differ from those of [Reference Lam and ShimozonoLS], which are more analogous to power-sum functions. For instance, the latter are a basis only over
$\widetilde {m}_k(x|\!|a)$
. In general, however, the double monomial functions defined here differ from those of [Reference Lam and ShimozonoLS], which are more analogous to power-sum functions. For instance, the latter are a basis only over ![]() .
.
The
![]() $m_\lambda (\xi |a)$
are closer to the double monomial functions
$m_\lambda (\xi |a)$
are closer to the double monomial functions
![]() $m_\lambda (x|\!|a)$
introduced by Molev [Reference MolevM, Section 5], which are defined non-explicitly via Hopf algebra duality, but do form a basis over
$m_\lambda (x|\!|a)$
introduced by Molev [Reference MolevM, Section 5], which are defined non-explicitly via Hopf algebra duality, but do form a basis over ![]() . They are not quite identical, as can be seen from the table in [Reference Lam and ShimozonoLS, Section 8.1], but in small examples the image of our
. They are not quite identical, as can be seen from the table in [Reference Lam and ShimozonoLS, Section 8.1], but in small examples the image of our
![]() $m_\lambda (\xi |a)$
under the substitution
$m_\lambda (\xi |a)$
under the substitution
![]() $a_i\mapsto -a_{1-i}$
agrees with the result of setting
$a_i\mapsto -a_{1-i}$
agrees with the result of setting
![]() $a_1=0$
in Molev’s function
$a_1=0$
in Molev’s function
![]() $m_\lambda (x|\!|a)$
. It would be interesting to know if this pattern persists.
$m_\lambda (x|\!|a)$
. It would be interesting to know if this pattern persists.
6 Moduli of vector bundles
The affine Grassmannian
![]() $\widetilde {\mathrm {Gr}}_n^d$
is homotopy-equivalent to the moduli stack parameterizing rank-n, degree d vector bundles on
$\widetilde {\mathrm {Gr}}_n^d$
is homotopy-equivalent to the moduli stack parameterizing rank-n, degree d vector bundles on ![]() together with a trivialization at
together with a trivialization at
![]() $\infty $
. Forgetting the trivialization identifies the moduli stack of vector bundles on
$\infty $
. Forgetting the trivialization identifies the moduli stack of vector bundles on ![]() with the quotient stack
with the quotient stack
![]() $[GL_n\backslash \widetilde {\mathrm {Gr}}_n^d]$
. (See, e.g., [Reference LarsonLa] for constructions of the moduli stacks, as well as further references, and [Reference ZhuZ, Section 4] for a careful exposition of the relation between moduli of bundles and affine Grassmannians.)
$[GL_n\backslash \widetilde {\mathrm {Gr}}_n^d]$
. (See, e.g., [Reference LarsonLa] for constructions of the moduli stacks, as well as further references, and [Reference ZhuZ, Section 4] for a careful exposition of the relation between moduli of bundles and affine Grassmannians.)
Larson gave an algebraic description of the Chow ring of the moduli stack
![]() $\mathcal {B}^\dagger _{n,d}$
of rank n, degree d vector bundles on
$\mathcal {B}^\dagger _{n,d}$
of rank n, degree d vector bundles on ![]() , as a certain subring of a polynomial ring [Reference LarsonLa]. In our context, the Chow and singular cohomology rings are isomorphic, and it follows from the above considerations that this ring must be isomorphic to the equivariant cohomology ring
, as a certain subring of a polynomial ring [Reference LarsonLa]. In our context, the Chow and singular cohomology rings are isomorphic, and it follows from the above considerations that this ring must be isomorphic to the equivariant cohomology ring
![]() $H_{GL_n}^*\widetilde {\mathrm {Gr}}_n^d$
. Here we will show that Larson’s description is equivalent to the presentation given above in Corollary A, using some basic identities of symmetric functions.
$H_{GL_n}^*\widetilde {\mathrm {Gr}}_n^d$
. Here we will show that Larson’s description is equivalent to the presentation given above in Corollary A, using some basic identities of symmetric functions.
Consider the polynomial ring ![]() , with
, with
![]() $e_i$
and
$e_i$
and
![]() $q_i$
in degree
$q_i$
in degree
![]() $2i$
. Larson shows that
$2i$
. Larson shows that
![]() $H^*\mathcal {B}^\dagger _{n,d} = H_{GL_n}^*\widetilde {\mathrm {Gr}}_n^d$
is isomorphic to the subring generated over
$H^*\mathcal {B}^\dagger _{n,d} = H_{GL_n}^*\widetilde {\mathrm {Gr}}_n^d$
is isomorphic to the subring generated over ![]() by the coefficients of a series
by the coefficients of a series
![]() $\overline {C}(t) = \sum _{k\geq 0} \overline {c}_k\, t^k$
, defined by
$\overline {C}(t) = \sum _{k\geq 0} \overline {c}_k\, t^k$
, defined by
 $$ \begin{align} \exp\left( \int \frac{-d(e_1+e_2 t+ \cdots + e_n t^{n-1}) + (q_1+q_2\, t + \cdots + q_{n-1}\, t^{n-2})}{1 + e_1 t + \cdots + e_n t^{n}}\,dt \right). \end{align} $$
$$ \begin{align} \exp\left( \int \frac{-d(e_1+e_2 t+ \cdots + e_n t^{n-1}) + (q_1+q_2\, t + \cdots + q_{n-1}\, t^{n-2})}{1 + e_1 t + \cdots + e_n t^{n}}\,dt \right). \end{align} $$
(To compare with Larson’s notation, our
![]() $\overline {c}_i$
is her
$\overline {c}_i$
is her
![]() $e_i$
, our
$e_i$
, our
![]() $e_i$
is her
$e_i$
is her
![]() $a_i$
, and our
$a_i$
, and our
![]() $q_i$
is her
$q_i$
is her
![]() $-a^{\prime }_{i+1}$
.)
$-a^{\prime }_{i+1}$
.)
Proposition 6.1 The ideal
![]() $J_n^d$
is the kernel of the
$J_n^d$
is the kernel of the ![]() -algebra homomorphism
-algebra homomorphism ![]() which sends
which sends
![]() $c_k$
to
$c_k$
to
![]() $\overline {c}_k$
. In particular, the
$\overline {c}_k$
. In particular, the ![]() -subalgebra of
-subalgebra of ![]() generated by the
generated by the
![]() $\overline {c}_k$
is isomorphic to
$\overline {c}_k$
is isomorphic to
![]() $\Lambda [e_1,\ldots ,e_n]/J_n^d \cong H_{GL_n}^*\widetilde {\mathrm {Gr}}_n^d$
.
$\Lambda [e_1,\ldots ,e_n]/J_n^d \cong H_{GL_n}^*\widetilde {\mathrm {Gr}}_n^d$
.
Proof Consider a generating series
along with
 $$ \begin{align} C(t) = \exp\left( \int \frac{-d(e_1+e_2 t+ \cdots + e_n t^{n-1}) + Q(t)}{E(t)}\,dt \right), \end{align} $$
$$ \begin{align} C(t) = \exp\left( \int \frac{-d(e_1+e_2 t+ \cdots + e_n t^{n-1}) + Q(t)}{E(t)}\,dt \right), \end{align} $$
where
![]() $E(t) = \sum _{k=0}^n e_k t^k$
as usual. The coefficients
$E(t) = \sum _{k=0}^n e_k t^k$
as usual. The coefficients
![]() $c_k$
are algebraically independent, so this formula defines an embedding
$c_k$
are algebraically independent, so this formula defines an embedding ![]() . The elements
. The elements
![]() $\overline {c}_k$
defined by (6.1) are the images of
$\overline {c}_k$
defined by (6.1) are the images of
![]() $c_k$
under the projection
$c_k$
under the projection
which sets
![]() $q_k$
to
$q_k$
to
![]() $0$
for
$0$
for
![]() $k\geq n$
. So it suffices to identify these
$k\geq n$
. So it suffices to identify these
![]() $q_k$
with the generators of
$q_k$
with the generators of
![]() $J_n^d$
.
$J_n^d$
.
Rewriting the expression (6.2), we find
where the series
![]() $P(t) = \frac {d}{dt}\log C(t)$
is determined by the Newton relations, in the form given in (3.2). Extracting the coefficient of
$P(t) = \frac {d}{dt}\log C(t)$
is determined by the Newton relations, in the form given in (3.2). Extracting the coefficient of
![]() $t^k$
, we see
$t^k$
, we see
![]() $q_k = p_k(c|e)+d\, e_k$
for all
$q_k = p_k(c|e)+d\, e_k$
for all
![]() $k\geq 1$
. In particular,
$k\geq 1$
. In particular,
![]() $q_n = p_n(c|e)+ d\, e_n$
, and
$q_n = p_n(c|e)+ d\, e_n$
, and
![]() $q_k = p_k(c|e)$
for
$q_k = p_k(c|e)$
for
![]() $k>n$
.
$k>n$
.
Acknowledgments
Thomas Lam very helpfully pointed me to references for other presentations of the equivariant cohomology of the affine Grassmannian. I thank Linda Chen, Hannah Larson, and Isabel Vogt for many conversations about the cohomology of the affine Grassmannian and the moduli stack of vector bundles. Thanks also to the referee for suggesting improvements to the exposition.




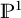 .
.
