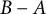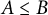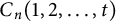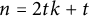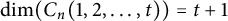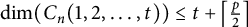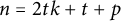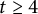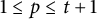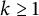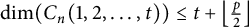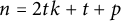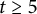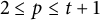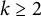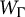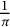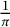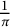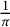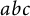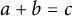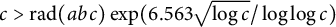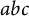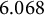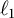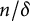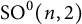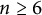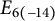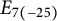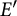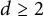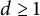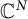Most read
This page lists the top ten most read articles for this journal based on the number of full text views and downloads recorded on Cambridge Core over the last 90 days. This list is updated on a daily basis.
Problems for generalized Monge–Ampère equations
- Part of:
-
- Published online by Cambridge University Press:
- 11 September 2023, pp. 265-278
-
- Article
- Export citation
Every symmetric Kubo–Ando connection has the order-determining property
- Part of:
-
- Published online by Cambridge University Press:
- 11 September 2023, pp. 279-288
-
- Article
- Export citation
Convexity of the radial sum of a star body and a ball
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2023, pp. 289-303
-
- Article
- Export citation
On theorems of Fermat, Wilson, and Gegenbauer
- Part of:
-
- Published online by Cambridge University Press:
- 12 September 2023, pp. 304-317
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Piecewise contracting maps on the interval: Hausdorff dimension, entropy, and attractors
- Part of:
-
- Published online by Cambridge University Press:
- 21 September 2023, pp. 318-327
-
- Article
- Export citation
On the metric dimension of circulant graphs
- Part of:
-
- Published online by Cambridge University Press:
- 28 September 2023, pp. 328-337
-
- Article
- Export citation
A new upper bound for the asymptotic dimension of RACGs
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2023, pp. 338-349
-
- Article
- Export citation
Ramanujan-type series for
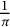 $\frac {1}{\pi }$, revisited
$\frac {1}{\pi }$, revisited
- Part of:
-
- Published online by Cambridge University Press:
- 05 October 2023, pp. 350-368
-
- Article
- Export citation
A new lower bound in the
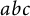 $abc$ conjecture
$abc$ conjecture
- Part of:
-
- Published online by Cambridge University Press:
- 09 October 2023, pp. 369-378
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounded cohomology is not a profinite invariant
- Part of:
-
- Published online by Cambridge University Press:
- 20 October 2023, pp. 379-390
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Universal spaces for asymptotic dimension via factorization
- Part of:
-
- Published online by Cambridge University Press:
- 20 October 2023, pp. 391-402
-
- Article
- Export citation
Some results on various types of compactness of weak* Dunford–Pettis operators on Banach lattices
- Part of:
-
- Published online by Cambridge University Press:
- 23 October 2023, pp. 403-414
-
- Article
- Export citation
Bregman distance regularization for nonsmooth and nonconvex optimization
-
- Published online by Cambridge University Press:
- 26 October 2023, pp. 415-424
-
- Article
- Export citation
Eisenstein congruences among Euler systems
- Part of:
-
- Published online by Cambridge University Press:
- 06 November 2023, pp. 425-446
-
- Article
- Export citation
Norms on complex matrices induced by random vectors II: extension of weakly unitarily invariant norms
- Part of:
-
- Published online by Cambridge University Press:
- 06 November 2023, pp. 447-457
-
- Article
- Export citation
Linear fractional self-maps of the unit ball
- Part of:
-
- Published online by Cambridge University Press:
- 15 November 2023, pp. 458-468
-
- Article
- Export citation
Remarks on Naimark dilation theorem
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2023, pp. 469-477
-
- Article
- Export citation
Selection principles and proofs from the Book
- Part of:
-
- Published online by Cambridge University Press:
- 23 November 2023, pp. 478-492
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological stability for homeomorphisms with global attractor
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2023, pp. 493-503
-
- Article
- Export citation
Truncations of generalized shift-invariant systems
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2023, pp. 504-515
-
- Article
- Export citation