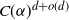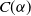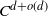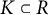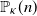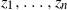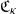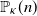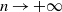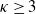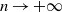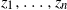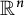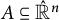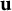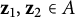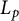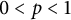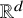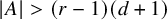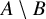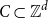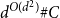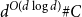318 results in 52Axx
Estranged facets and k-facets of Gaussian random point sets
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-17
-
- Article
- Export citation
On the perimeter, diameter and circumradius of ordinary hyperbolic reduced polygons
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 28 February 2025, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral Polyhedra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 06 February 2025, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probability that n points are in convex position in a regular κ-gon: Asymptotic results
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 17 January 2025, pp. 1-60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Additive kinematic formulas for convex functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measure comparison problems for dilations of convex bodies
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 270-285
- Print publication:
- March 2025
-
- Article
- Export citation
On polar convexity in finite-dimensional Euclidean spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-37
-
- Article
-
- You have access
- HTML
- Export citation
The discrete Orlicz chord Minkowski problem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 09 December 2024, pp. 154-165
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation
Equality cases of the Alexandrov–Fenchel inequality are not in the polynomial hierarchy
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 November 2024, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal transport through a toll station
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigidity for the perimeter inequality under Schwarz symmetrization
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sums of squares, Hankel index and almost real rank
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 30 May 2024, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Series expansions for random disc-polygons in smooth plane convex bodies
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1407-1423
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extensions of the colorful Helly theorem for d-collapsible and d-Leray complexes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp bounds for a discrete John’s theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 484-486
-
- Article
-
- You have access
- HTML
- Export citation
On the cross-product conjecture for the number of linear extensions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 19 January 2024, pp. 535-562
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Affine isoperimetric inequalities on flag manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 19 December 2023, pp. 252-281
- Print publication:
- February 2025
-
- Article
- Export citation
Convexity of the radial sum of a star body and a ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 04 September 2023, pp. 289-303
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
A minimax inequality for inscribed cones revisited
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 31 August 2023, pp. 215-221
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
ON SEPARATE CONTINUITY AND SEPARATE CONVEXITY: A SYNTHETIC TREATMENT FOR FUNCTIONS AND SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 541-551
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation