Article contents
Turing degrees and many-one degrees of maximal sets
Published online by Cambridge University Press: 12 March 2014
Extract
Martin [4, Theorems 1 and 2] proved that a Turing degree a is the degree of a maximal set if, and only if, a′ = 0″. Lachlan has shown that maximal sets have minimal many-one degrees [2, §1] and that every nonrecursive r.e. Turing degree contains a minimal many-one degree [2, Theorem 4]. Our aim here is to show that any r.e. Turing degree a of a maximal set contains an infinite number of maximal sets whose many-one degrees are pairwise incomparable; hence such Turing degrees contain an infinite number of distinct minimal many-one degrees. This theorem has been proved by Yates [6, Theorem 5] in the case when a = 0′.
The need for this theorem first came to our attention as a result of work done by the author [3, Theorem 2.3]. There we looked at the structure 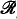 /
/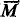 obtained from the recursive functions of one variable under the equivalence relation f ~ g if, and only if, f(x) = g(x) a.e., that is, for all but finitely many x ∈
obtained from the recursive functions of one variable under the equivalence relation f ~ g if, and only if, f(x) = g(x) a.e., that is, for all but finitely many x ∈ 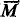 , where M is a maximal set, and M is its complement. We showed that
, where M is a maximal set, and M is its complement. We showed that 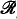 /
/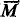 1 ≡
1 ≡ 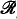 /
/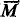 2 if, and only if,
2 if, and only if, 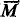 1 =
m
1 =
m
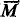 2, i.e.,
2, i.e., 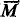 1. and
1. and 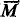 2 have the same many-one degree. However, it might be possible that some Turing degree of a maximal set contains exactly one many-one degree of a maximal set. Theorem 1 was proved to show that this was not the case, and hence that the theory of
2 have the same many-one degree. However, it might be possible that some Turing degree of a maximal set contains exactly one many-one degree of a maximal set. Theorem 1 was proved to show that this was not the case, and hence that the theory of 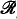 /
/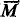 is not an invariant of Turing degree.
is not an invariant of Turing degree.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1970
Footnotes
This research was supported in part by National Science Foundation grant GP-7524 and is part of the author's doctoral thesis written under the direction of Professor Anil Nerode.
References
- 3
- Cited by


