Research Article
Algebraic completeness results for R-mingle and its extensions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-13
-
- Article
- Export citation
The number of countable models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 14-18
-
- Article
- Export citation
On an algebra of sets of finite sequences 1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 19-28
-
- Article
- Export citation
Turing degrees and many-one degrees of maximal sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 29-40
-
- Article
- Export citation
A theorem on initial segments of degrees 1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 41-45
-
- Article
- Export citation
On a question of G. E. Sacks 1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 46-50
-
- Article
- Export citation
A universal embedding property of the RETs
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 51-59
-
- Article
- Export citation
Every analytic set is Ramsey
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 60-64
-
- Article
- Export citation
Almost combinatorial Skolem functions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 65-72
-
- Article
- Export citation
On theories T categorical in |T|
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 73-82
-
- Article
- Export citation
On the cardinality of ultraproduct of finite sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 83-84
-
- Article
- Export citation
Bases and α-dimensions of countable vector spaces with recursive operations 1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 85-96
-
- Article
- Export citation
An algebraic characterization of indistinguishable cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 97-104
-
- Article
- Export citation
Tense logic for discrete future time
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 105-118
-
- Article
- Export citation
A problem in the theory of constructive order types 1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 119-121
-
- Article
- Export citation
Reviews
Reviews - Ernest A. Moody. The medieval contribution to logic. Studium generale, vol. 19 (1966), pp. 443–452. - Ernest A. Moody. A quodlibetal question of Robert Holkot, O.P., on the problem of the objects of knowledge and of belief. Speculum, vol. 39 (1964), pp. 53–74. - Ernest A. Moody. Buridan and a dilemma of nominalism. Harry Austryn Wolfson jubilee volume, English section, vol. 2, American Academy for Jewish Research, Jerusalem 1965, pp. 577–596.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 122-124
-
- Article
- Export citation
David Miller. A paradox of information. The British journal for the philosophy of science, vol. 17 no. 1 (1966), pp. 59–61. - Karl R. Popper. A comment on Miller's new paradox of information. The British journal for the philosophy of science, vol. 17 no. 1 (1966), pp. 61–69. - Karl R. Popper. A paradox of zero information. The British journal for the philosophy of science, vol. 17 no. 2, pp. 141–143. - J. L. Mackie. Miller's so-called paradox of information. The British journal for the philosophy of science, vol. 17 no. 2, pp. 144–147. - David Miller. On a so-called so-called paradox: a reply to Professor J. L. Mackie. The British journal for the philosophy of science, vol. 17 no. 2, pp. 147–149. - Jeffrey Bub and Michael Radner. Miller's paradox of information. The British journal for the philosophy of science, vol. 19 no. 1 (1968), pp. 63–67. - David Miller. The straight and narrow rule of induction: a reply to Dr Bub and Mr Radner. The British journal for the philosophy of science, vol. 19 no. 2, pp. 145–151. - William W. Rozeboom. New mysteries for old: the transfiguration of Miller's paradox. The British journal for the philosophy of science, vol. 19 no. 4, pp. 345–353.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 124-127
-
- Article
- Export citation
Henry E. KyburgJr. , Probability and the logic of rational belief. Wesleyan University Press, Middletown, Conn., 1961, x + 350 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 127-128
-
- Article
- Export citation
Henry E. KyburgJr. , Probability and randomness. Theoria (Lund), vol. 29 (1963), pp. 27–55.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 129
-
- Article
- Export citation
Henry E. KyburgJr. , Demonstrative induction. Philosophy and phenomenological research, vol. 21 no. 1 (1960), pp. 80–92.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 129
-
- Article
- Export citation

 nonisomorphic countable models. It has been conjected (e.g., in [4]) that if it has an uncountable number of such models then it has exactly
nonisomorphic countable models. It has been conjected (e.g., in [4]) that if it has an uncountable number of such models then it has exactly 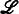 be an ℒ-structure. We assume that ℒ has a simple infinite sequence
be an ℒ-structure. We assume that ℒ has a simple infinite sequence 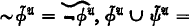
 cylindrifications
cylindrifications 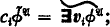 diagonal elements (0-ary operations)
diagonal elements (0-ary operations) 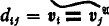 . In this way we make the class of all sets
. In this way we make the class of all sets 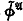 of all cylindric set algebras (of dimension
of all cylindric set algebras (of dimension 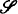 be the class of all algebras of sets of finite sequences (an exact definition is given in §1).
be the class of all algebras of sets of finite sequences (an exact definition is given in §1).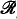 /
/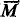 obtained from the recursive functions of one variable under the equivalence relation
obtained from the recursive functions of one variable under the equivalence relation 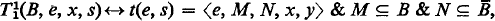
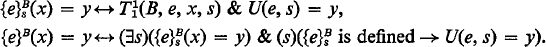
 be a version of class set theory admitting urelemente, and with AC (= axiom of choice) replaced by AC
be a version of class set theory admitting urelemente, and with AC (= axiom of choice) replaced by AC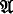 be an arbitrarily quantified positive first order sentence in functors for + and ·. Let ƒ
be an arbitrarily quantified positive first order sentence in functors for + and ·. Let ƒ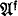 the universal sentence obtained from
the universal sentence obtained from 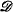 is an ultrafilter and
is an ultrafilter and 
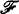 which itself is in some sense recursively enumerable and has recursive operations.
which itself is in some sense recursively enumerable and has recursive operations.