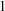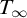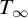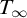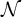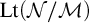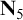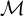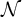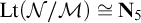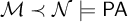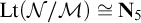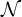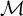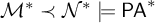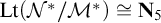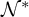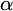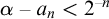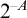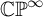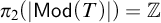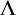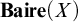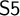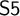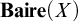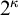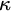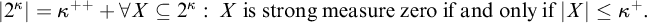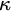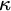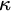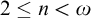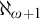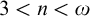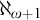Open access
Article
BUILDING MODELS IN SMALL CARDINALS IN LOCAL ABSTRACT ELEMENTARY CLASSES
- Part of:
-
- Published online by Cambridge University Press:
- 29 April 2024, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE DEFINABILITY OF THE EXTENDER SEQUENCE
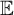 $\mathbb {E}$ FROM
$\mathbb {E}$ FROM 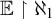 $\mathbb {E}\upharpoonright \aleph _1$ IN
$\mathbb {E}\upharpoonright \aleph _1$ IN 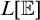 $L[\mathbb {E}]$
$L[\mathbb {E}]$
- Part of:
-
- Published online by Cambridge University Press:
- 15 April 2024, pp. 427-459
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE AMALGAMATION PROPERTY AND URYSOHN STRUCTURES IN CONTINUOUS LOGIC
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1-61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NONDEFINABILITY RESULTS FOR ELLIPTIC AND MODULAR FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Erratum
PAC STRUCTURES AS INVARIANTS OF FINITE GROUP ACTIONS – ERRATUM
-
- Published online by Cambridge University Press:
- 26 March 2024, p. 1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Article
WAND/SET THEORIES: A REALIZATION OF CONWAY’S MATHEMATICIANS’ LIBERATION MOVEMENT, WITH AN APPLICATION TO CHURCH’S SET THEORY WITH A UNIVERSAL SET
- Part of:
-
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE FRAGILITY OF INTERPOLATION
- Part of:
-
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO-CARDINAL DERIVED TOPOLOGIES, INDESCRIBABILITY AND RAMSEYNESS
- Part of:
-
- Published online by Cambridge University Press:
- 12 March 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NEW PERSPECTIVE ON SEMI-RETRACTIONS AND THE RAMSEY PROPERTY
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DUALITY FOR COALGEBRAS FOR VIETORIS AND MONADICITY
- Part of:
-
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON RANK NOT ONLY IN NSOP
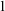 $_1$ THEORIES
$_1$ THEORIES
- Part of:
-
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE PENTAGON AS A SUBSTRUCTURE LATTICE OF MODELS OF PEANO ARITHMETIC
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REGAININGLY APPROXIMABLE NUMBERS AND SETS
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POLISH SPACE PARTITION PRINCIPLES AND THE HALPERN–LÄUCHLI THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 19 January 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NON-TRIVIAL HIGHER HOMOTOPY OF FIRST-ORDER THEORIES
- Part of:
-
- Published online by Cambridge University Press:
- 11 January 2024, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE BAIRE CLOSURE AND ITS LOGIC
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2024, pp. 27-49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STRONG MEASURE ZERO SETS ON
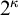 $2^\kappa $ FOR
$2^\kappa $ FOR 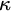 $\kappa $ INACCESSIBLE
$\kappa $ INACCESSIBLE
- Part of:
-
- Published online by Cambridge University Press:
- 03 January 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE STRONG AND SUPER TREE PROPERTIES AT SUCCESSORS OF SINGULAR CARDINALS
- Part of:
-
- Published online by Cambridge University Press:
- 22 December 2023, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTROENUMERABILITY, AUTOREDUCIBILITY, AND RANDOMNESS
- Part of:
-
- Published online by Cambridge University Press:
- 12 December 2023, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO EXAMPLES CONCERNING EXISTENTIAL UNDECIDABILITY IN FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 23 November 2023, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

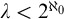
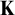
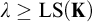
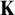
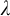
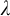
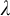
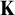
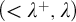
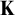
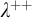
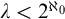
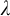
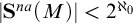
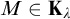
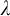
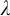
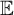
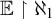
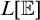























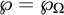
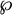
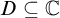
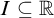
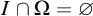
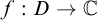
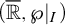
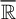
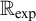
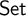
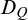
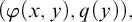
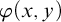
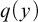
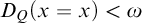
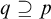
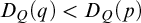
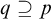
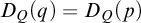
 -stationary. We give natural examples of families of invariant types satisfying this property in some NSOP
-stationary. We give natural examples of families of invariant types satisfying this property in some NSOP