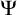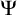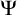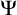1. Introduction
In 1959, Friedberg and Rogers [Reference Friedberg and Rogers4] introduced enumeration reducibility. A set
![]() $A\subseteq \omega $
is enumeration reducible to another set
$A\subseteq \omega $
is enumeration reducible to another set
![]() $B\subseteq \omega $
if there is a c.e. set W such that
$B\subseteq \omega $
if there is a c.e. set W such that
![]() $A=\lbrace x:(\exists y)\langle x,y\rangle \in W\mathrm {\ and\ }D_y\subseteq B\rbrace $
, where
$A=\lbrace x:(\exists y)\langle x,y\rangle \in W\mathrm {\ and\ }D_y\subseteq B\rbrace $
, where
![]() $\lbrace D_y\rbrace _{y\in \omega }$
gives a computable listing of all finite sets. We call the c.e. set W that witnesses this reduction an enumeration operator and write
$\lbrace D_y\rbrace _{y\in \omega }$
gives a computable listing of all finite sets. We call the c.e. set W that witnesses this reduction an enumeration operator and write
![]() $A=W(B)$
. The degree structure induced by enumeration reduction
$A=W(B)$
. The degree structure induced by enumeration reduction
![]() $\leq _e$
consists of the enumeration degrees. We can identify subsets of
$\leq _e$
consists of the enumeration degrees. We can identify subsets of
![]() $\omega $
with infinite strings in the Cantor space
$\omega $
with infinite strings in the Cantor space
![]() $2^{\omega }$
. Therefore, we can consider the measure of different classes of enumeration degrees (often abbreviated by e-degrees), including cototal e-degrees, uniformly introenumerable e-degrees, introenumerable e-degrees, and hyper-cototal e-degrees.
$2^{\omega }$
. Therefore, we can consider the measure of different classes of enumeration degrees (often abbreviated by e-degrees), including cototal e-degrees, uniformly introenumerable e-degrees, introenumerable e-degrees, and hyper-cototal e-degrees.
Given a set A of natural numbers and any number n, we may ask whether the membership of n in A can be determined using the oracle A without asking “is n in A”. If so, A has a kind of self-reducibility. The notion of autoreducibility introduced by Trakhtenbrot [Reference Trakhtenbrot12] in 1970 is a formalization of this idea. A set A is said to be autoreducible if there is a Turing functional
![]() $\Phi $
such that for any n,
$\Phi $
such that for any n,
![]() $A(n)=\Phi ^{A-\lbrace n\rbrace }(n)$
. We will generalize the autoreduction notion by defining
$A(n)=\Phi ^{A-\lbrace n\rbrace }(n)$
. We will generalize the autoreduction notion by defining
![]() $\Psi $
-autoreducibility for any autoreduction procedure
$\Psi $
-autoreducibility for any autoreduction procedure
![]() $\Psi $
, which is a function from
$\Psi $
, which is a function from
![]() $\omega \times 2^{\omega }$
to
$\omega \times 2^{\omega }$
to
![]() $\lbrace 0,1\rbrace $
. The classes of enumeration degrees mentioned above all have natural autoreducibility by replacing the Turing functional with different autoreduction procedures. Next, we will show that any measurable class of
$\lbrace 0,1\rbrace $
. The classes of enumeration degrees mentioned above all have natural autoreducibility by replacing the Turing functional with different autoreduction procedures. Next, we will show that any measurable class of
![]() $\Psi $
-autoreducible sets has measure zero for any
$\Psi $
-autoreducible sets has measure zero for any
![]() $\Psi $
. Then, we use this property of classes of
$\Psi $
. Then, we use this property of classes of
![]() $\Psi $
-autoreducible sets to show that the classes of above e-degrees all have measure zero.
$\Psi $
-autoreducible sets to show that the classes of above e-degrees all have measure zero.
Intuitively, given a set
![]() $A\subseteq \omega $
, or equivalently an infinite string in
$A\subseteq \omega $
, or equivalently an infinite string in
![]() $2^{\omega }$
, it is random if it is hard to compress or one cannot predict the next bit or it has no rare properties. In 1966, Martin-Löf introduced a randomness notion using the latter idea that a random set is in no effective measure zero set in [Reference Martin-Löf8]. An infinite string
$2^{\omega }$
, it is random if it is hard to compress or one cannot predict the next bit or it has no rare properties. In 1966, Martin-Löf introduced a randomness notion using the latter idea that a random set is in no effective measure zero set in [Reference Martin-Löf8]. An infinite string
![]() $A\in 2^{\omega }$
is Martin-Löf random (n-random), if A is not in
$A\in 2^{\omega }$
is Martin-Löf random (n-random), if A is not in
![]() $\bigcap _m G_m$
, where
$\bigcap _m G_m$
, where
![]() $\lbrace G_m\rbrace _{m\in \omega }$
is any uniformly
$\lbrace G_m\rbrace _{m\in \omega }$
is any uniformly
![]() $\Sigma ^0_1$
(
$\Sigma ^0_1$
(
![]() $\Sigma ^0_n$
, respectively) sequence of open sets such that the measure of each
$\Sigma ^0_n$
, respectively) sequence of open sets such that the measure of each
![]() $G_m$
is smaller than
$G_m$
is smaller than
![]() $2^{-m}$
. A set A is weakly n-random if A avoids all
$2^{-m}$
. A set A is weakly n-random if A avoids all
![]() $\Pi ^0_n$
classes. Generally, a set is random if it avoids a particular kind of null classes. Such null classes can be arithmetical as above or even go beyond arithmetical.
$\Pi ^0_n$
classes. Generally, a set is random if it avoids a particular kind of null classes. Such null classes can be arithmetical as above or even go beyond arithmetical.
Since our classes of e-degrees have measure zero, sufficiently random sets must avoid such measure zero classes. Therefore, we can ask questions about what level of randomness the above sets or e-degrees can reach, and what level of randomness the above sets or e-degrees must avoid. We answer such questions for cototal sets, cototal e-degrees, uniformly introenumerable sets, uniformly introenumerable e-degrees, introenumerable sets, and introenumerable e-degrees. For references for randomness notions, see [Reference Downey and Hirschfeldt2] or [Reference Nies10].
We start by giving the definitions of the sets and e-degrees we mentioned. First, a set A is total if
![]() $\overline {A}\leq _e A$
. It is named total because the degree of a total set is the degree of the graph of a total function. In [Reference Andrews, Ganchev, Kuyper, Lempp, Miller, Soskova and Soskova1], the notion of cototality is given by reversing the relationship between A and
$\overline {A}\leq _e A$
. It is named total because the degree of a total set is the degree of the graph of a total function. In [Reference Andrews, Ganchev, Kuyper, Lempp, Miller, Soskova and Soskova1], the notion of cototality is given by reversing the relationship between A and
![]() $\overline {A}$
.
$\overline {A}$
.
Definition 1.1. A set A is cototal when
![]() $A\leq _e\overline {A}$
.
$A\leq _e\overline {A}$
.
Definition 1.2. An infinite set X is uniformly introenumerable if there is an enumeration operator
![]() $\Gamma $
such that for every infinite subset Y of X,
$\Gamma $
such that for every infinite subset Y of X,
![]() $\Gamma (Y)=X$
.
$\Gamma (Y)=X$
.
In [Reference Jockusch7], Jockush introduced the notion of uniform introenumerability. The definition of uniform introenumerability we give here is slightly different by using an enumeration operator instead of a c.e. operator, though the two definitions were shown to be equivalent in [Reference Greenberg, Harrison-Trainor, Patey and Turetsky6] by Greenberg et al. Recently, Goh et al. [Reference Le Goh, Jacobsen-Grocott, Miller and Soskova5] also showed that Jockush’s notion of (non-uniform) introenumerability is equivalent to the following notion:
Definition 1.3. An infinite set X is introenumerable if, for every infinite subset Y of X, there is an enumeration operator
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\Gamma (Y)=X$
.
$\Gamma (Y)=X$
.
In [Reference Sanchis11], Sanchis introduced a reduction that is related to hyperarithmetical reduction and only uses positive information about membership in the set:
Definition 1.4. Let A and B be sets such that, for some c.e. set W, the following relation holds:
![]() $x\in B$
if and only if
$x\in B$
if and only if
Then we say that B is hyper-enumeration reducible to A and write this relation:
![]() $B\leq _{he}A$
.
$B\leq _{he}A$
.
Definition 1.5. A is called hyper-cototal if
![]() $A \leq _{he}\overline {A}$
.
$A \leq _{he}\overline {A}$
.
Theorem 1.6. The relationship of enumeration degrees of the above notions is the following:
 $$ \begin{align*} \textit{Cototal} & \rightarrow\textit{Uniformly Introenumerable}\\ & \dashrightarrow\textit{Introenumerable}\rightarrow\textit{Hyper-cototal}. \end{align*} $$
$$ \begin{align*} \textit{Cototal} & \rightarrow\textit{Uniformly Introenumerable}\\ & \dashrightarrow\textit{Introenumerable}\rightarrow\textit{Hyper-cototal}. \end{align*} $$
Remark 1.7. The solid arrows are strict. For proof of the first arrow, see [Reference McCarthy9]. The third arrow and the strictness of the first arrow are proved in [Reference Le Goh, Jacobsen-Grocott, Miller and Soskova5] by Goh et al. It is still unknown whether there is a set of introenumerable e-degree that does not have uniformly introenumerable e-degree.
2. Measure of classes with autoreduction
In this section, we define
![]() $\Psi $
-autoreducible sets given an autoreduction procedure
$\Psi $
-autoreducible sets given an autoreduction procedure
![]() $\Psi $
and show that any measurable class of
$\Psi $
and show that any measurable class of
![]() $\Psi $
-autoreduction sets has measure zero. Next, we apply the autoreducibility of hyper-cototal e-degrees to show that the measure of the class of such e-degrees is zero.
$\Psi $
-autoreduction sets has measure zero. Next, we apply the autoreducibility of hyper-cototal e-degrees to show that the measure of the class of such e-degrees is zero.
Definition 2.1. Given a function
![]() $\Psi :\omega \times 2^{\omega }\rightarrow \lbrace 0,1\rbrace $
, A set A is
$\Psi :\omega \times 2^{\omega }\rightarrow \lbrace 0,1\rbrace $
, A set A is
![]() $\Psi $
-autoreducible if and only if
$\Psi $
-autoreducible if and only if
Here, we say that the function
![]() $\Psi $
is an autoreduction procedure.
$\Psi $
is an autoreduction procedure.
Next, to show that the measure of a class of
![]() $\Psi $
-autoreducible sets is zero, we use the Lebesgue density theorem.
$\Psi $
-autoreducible sets is zero, we use the Lebesgue density theorem.
Theorem 2.2. Fix an autoreduction procedure
![]() $\Psi $
, a measurable class S of
$\Psi $
, a measurable class S of
![]() $\Psi $
-autoreducible sets has measure zero.
$\Psi $
-autoreducible sets has measure zero.
Proof Suppose a class S of
![]() $\Psi $
-autoreducible sets has positive measure. By the Lebesgue density theorem, for any
$\Psi $
-autoreducible sets has positive measure. By the Lebesgue density theorem, for any
![]() $\varepsilon>0$
, there is a string
$\varepsilon>0$
, there is a string
![]() $\sigma \in 2^{<\omega }$
such that
$\sigma \in 2^{<\omega }$
such that
![]() $\frac {\mu (S\cap \lbrack \sigma \rbrack )}{\mu (S)}\geq 1-\varepsilon $
. Fix
$\frac {\mu (S\cap \lbrack \sigma \rbrack )}{\mu (S)}\geq 1-\varepsilon $
. Fix
![]() $\varepsilon =\frac {1}{4}$
along with the corresponding string
$\varepsilon =\frac {1}{4}$
along with the corresponding string
![]() $\sigma $
. Consider an
$\sigma $
. Consider an
![]() $n\in \omega $
larger than
$n\in \omega $
larger than
![]() $|\sigma |$
. Define subsets
$|\sigma |$
. Define subsets
![]() $P_i (i=0,1)$
of S as follows:
$P_i (i=0,1)$
of S as follows:
Since
![]() $P_0$
and
$P_0$
and
![]() $P_1$
partition S, one of them must have the following relative measure:
$P_1$
partition S, one of them must have the following relative measure:
![]() $\frac {\mu (P_i\cap \lbrack \sigma \rbrack )}{\mu (S)}\geq \frac {1-\varepsilon }{2}=\frac {3}{8}$
. Without loss of generality, assume that such subset is
$\frac {\mu (P_i\cap \lbrack \sigma \rbrack )}{\mu (S)}\geq \frac {1-\varepsilon }{2}=\frac {3}{8}$
. Without loss of generality, assume that such subset is
![]() $P_0$
. Now, consider the set
$P_0$
. Now, consider the set
Notice that if
![]() $x\in P_0$
,
$x\in P_0$
,
![]() $X(n)=0$
. So,
$X(n)=0$
. So,
![]() $P_2$
also has relative measure
$P_2$
also has relative measure
![]() $\frac {\mu (P_2\cap \lbrack \sigma \rbrack )}{\mu (S)}\geq \frac {3}{8}>\frac {1}{4}$
. Therefore,
$\frac {\mu (P_2\cap \lbrack \sigma \rbrack )}{\mu (S)}\geq \frac {3}{8}>\frac {1}{4}$
. Therefore,
![]() $\frac {\mu (P_2\cap S\cap \lbrack \sigma \rbrack )}{\mu (S)}>0$
. So,
$\frac {\mu (P_2\cap S\cap \lbrack \sigma \rbrack )}{\mu (S)}>0$
. So,
![]() $P_2\cap S$
is not empty. For any
$P_2\cap S$
is not empty. For any
![]() $Y\in P_2\cap S$
,
$Y\in P_2\cap S$
,
![]() $\Psi (n,Y-\lbrace n\rbrace )=0\not =1=Y(n)$
. This is a contradiction. Therefore, S has measure zero.
$\Psi (n,Y-\lbrace n\rbrace )=0\not =1=Y(n)$
. This is a contradiction. Therefore, S has measure zero.
Remark 2.3. In this theorem, the assumption that the class S is measurable is necessary. Consider the finite difference equivalence classes: two sets A and B are in the same equivalence class if and only
![]() $(A-B)\cup (B-A)$
is finite. Now, we can define a class
$(A-B)\cup (B-A)$
is finite. Now, we can define a class
![]() $S_0$
that contains exactly one element from each of the equivalence classes. It is not difficult to see that
$S_0$
that contains exactly one element from each of the equivalence classes. It is not difficult to see that
![]() $S_0$
is not measurable. We can define a function
$S_0$
is not measurable. We can define a function
![]() $\Psi _0$
such that if
$\Psi _0$
such that if
![]() $A\in S_0$
and
$A\in S_0$
and
![]() $n\in \omega $
, then
$n\in \omega $
, then
![]() $\Psi _0(n,A-\lbrace n\rbrace )=A(n)$
. It is well-defined because, for any
$\Psi _0(n,A-\lbrace n\rbrace )=A(n)$
. It is well-defined because, for any
![]() $B\in S_0$
and
$B\in S_0$
and
![]() $B-\lbrace n\rbrace =A-\lbrace n\rbrace $
,
$B-\lbrace n\rbrace =A-\lbrace n\rbrace $
,
![]() $\Psi _0(n,B-\lbrace n\rbrace )$
has to equal
$\Psi _0(n,B-\lbrace n\rbrace )$
has to equal
![]() $A(n)$
by the definition of
$A(n)$
by the definition of
![]() $S_0$
. Therefore,
$S_0$
. Therefore,
![]() $S_0$
is a class consisting of
$S_0$
is a class consisting of
![]() $\Psi _0$
-autoreducible sets that does not have measure zero since it is not measurable.
$\Psi _0$
-autoreducible sets that does not have measure zero since it is not measurable.
Now we use the above theorem to show that the measure of the class of hyper-cototal e-degrees is zero. First, we discuss the autoreducibility of hyper-cototal sets.
Lemma 2.4. For every hyper-cototal set A, there is a
![]() $\Psi $
such that A is
$\Psi $
such that A is
![]() $\Psi $
-autoreducible.
$\Psi $
-autoreducible.
Proof Suppose A is hyper-cototal and there is some hyper-enumeration operator
![]() $\Delta $
such that
$\Delta $
such that
![]() $A=\Delta (\overline {A})$
. When
$A=\Delta (\overline {A})$
. When
![]() $n\in A$
,
$n\in A$
,
![]() $\overline {A}\subseteq \overline {A-\lbrace n\rbrace }$
. Therefore,
$\overline {A}\subseteq \overline {A-\lbrace n\rbrace }$
. Therefore,
![]() $n\in \Delta ^{\overline {A}}\subseteq \Delta ^{\overline {A-\lbrace n\rbrace }}$
. When
$n\in \Delta ^{\overline {A}}\subseteq \Delta ^{\overline {A-\lbrace n\rbrace }}$
. When
![]() $n\not \in A$
,
$n\not \in A$
,
![]() $n\not \in \Delta ^{\overline {A}}=\Delta ^{\overline {A-\lbrace n\rbrace }}$
. So,
$n\not \in \Delta ^{\overline {A}}=\Delta ^{\overline {A-\lbrace n\rbrace }}$
. So,
![]() $A(n)=\Delta ^{\overline {A-\lbrace n\rbrace }}(n)$
. Then, we can define
$A(n)=\Delta ^{\overline {A-\lbrace n\rbrace }}(n)$
. Then, we can define
![]() $\Psi (n,X):=\Delta ^{\overline {X}}(n)$
.
$\Psi (n,X):=\Delta ^{\overline {X}}(n)$
.
In fact, each set of hyper-cototal degree is
![]() $\Psi $
-autoreducible for some autoreduction procedure
$\Psi $
-autoreducible for some autoreduction procedure
![]() $\Psi $
as well.
$\Psi $
as well.
Lemma 2.5. Any set in the class of hyper-cototal e-degrees is a hyper-cototal set.
Proof In [Reference Sanchis11], Sanchis proved that If
![]() $A\leq _e B$
, then
$A\leq _e B$
, then
![]() $A\leq _{he} B$
and
$A\leq _{he} B$
and
![]() $\overline {A}\leq _{he}\overline {B}$
. Suppose A has hyper-cototal e-degree and
$\overline {A}\leq _{he}\overline {B}$
. Suppose A has hyper-cototal e-degree and
![]() $A\equiv _e B$
, where B is a hyper-cototal set. Then,
$A\equiv _e B$
, where B is a hyper-cototal set. Then,
![]() $A\equiv _{he} B\leq _{he}\overline {B}\equiv _{he}\overline {A}$
.
$A\equiv _{he} B\leq _{he}\overline {B}\equiv _{he}\overline {A}$
.
Next, in order to apply Theorem 2.2 to show that the measure of the classes of hyper-cototal e-degrees is 0, we first need to show that the class of hyper-cototal e-degrees is measurable by analyzing the arithmetical complexity of
Notice that
![]() $n\in \Gamma ^{\overline {A}}$
and
$n\in \Gamma ^{\overline {A}}$
and
![]() $n\not \in \Gamma ^{\overline {A}}$
are
$n\not \in \Gamma ^{\overline {A}}$
are
![]() $\Pi _1^1$
and
$\Pi _1^1$
and
![]() $\Sigma _1^1$
, respectively, for a hyper-enumeration operator
$\Sigma _1^1$
, respectively, for a hyper-enumeration operator
![]() $\Gamma $
by Definition 1.4. So, the class of hyper-cototal e-degrees is the difference of two
$\Gamma $
by Definition 1.4. So, the class of hyper-cototal e-degrees is the difference of two
![]() $\Pi _1^1$
classes. Recall that
$\Pi _1^1$
classes. Recall that
![]() $\Pi ^1_1$
sets are measurable. Therefore, the class of hyper-cototal e-degrees is measurable. Now, we use the results from above to see that the class of hyper-cototal e-degrees has measure zero.
$\Pi ^1_1$
sets are measurable. Therefore, the class of hyper-cototal e-degrees is measurable. Now, we use the results from above to see that the class of hyper-cototal e-degrees has measure zero.
Lemma 2.6. The classes of hyper-cototal, introenumerable, uniformly introenumerable, and cototal e-degrees all have measure zero.
Proof Suppose the class of hyper-cototal e-degrees has positive measure. Because there are only countably many hyper-enumeration operators, there exists a
![]() $\Gamma $
such that the class of hyper-cototal e-degrees witnessed by this operator has positive measure. However, any set in this class would be
$\Gamma $
such that the class of hyper-cototal e-degrees witnessed by this operator has positive measure. However, any set in this class would be
![]() $\Gamma $
-autoreducible by Lemma 2.4. Now, applying Theorem 2.2 gives us a contradiction. By the relationship between the e-degrees mentioned above in Theorem 1.6, we see that the measure of these classes are all zero.
$\Gamma $
-autoreducible by Lemma 2.4. Now, applying Theorem 2.2 gives us a contradiction. By the relationship between the e-degrees mentioned above in Theorem 1.6, we see that the measure of these classes are all zero.
3. Bounds of randomness
Notice that, for any class of measure zero, sufficiently random sets avoid it. So, we now discuss what level of randomness these e-degrees could and could not have. In this section, all necessary background knowledge of randomness is from Nies’ book [Reference Nies10]. We first discuss the class of cototal sets and the class of cototal e-degrees.
Theorem 3.1. Weakly 2-random sets are not cototal.
Proof The class of cototal sets
![]() $\lbrace A:A\leq _e \overline {A}\rbrace $
is defined by
$\lbrace A:A\leq _e \overline {A}\rbrace $
is defined by
 $$ \begin{align*} \bigcup_e\lbrace A:A=\Gamma_e^{\overline{A}}\rbrace= & \bigcup_e\lbrace A:\forall n\lbrack n\in A\rightarrow(\exists D_y\subseteq \overline{A})\lbrack\langle n,y\rangle\in\Gamma_e\rangle\rbrack\\ & \wedge n\not\in A\rightarrow (\forall y)\lbrack\langle n,y\rangle\in\Gamma_e \rightarrow D_y\cap A\not=\emptyset\rbrack\rbrack\rbrace, \end{align*} $$
$$ \begin{align*} \bigcup_e\lbrace A:A=\Gamma_e^{\overline{A}}\rbrace= & \bigcup_e\lbrace A:\forall n\lbrack n\in A\rightarrow(\exists D_y\subseteq \overline{A})\lbrack\langle n,y\rangle\in\Gamma_e\rangle\rbrack\\ & \wedge n\not\in A\rightarrow (\forall y)\lbrack\langle n,y\rangle\in\Gamma_e \rightarrow D_y\cap A\not=\emptyset\rbrack\rbrack\rbrace, \end{align*} $$
where
![]() $\Gamma _e$
’s are enumeration operators. Therefore, the class of cototal sets is a union of
$\Gamma _e$
’s are enumeration operators. Therefore, the class of cototal sets is a union of
![]() $\Pi ^0_2$
classes. By Lemma 2.6, all such classes have measure zero. Because any weakly 2-random set avoids all null
$\Pi ^0_2$
classes. By Lemma 2.6, all such classes have measure zero. Because any weakly 2-random set avoids all null
![]() $\Pi ^0_2$
classes, weakly 2-random sets are not cototal.
$\Pi ^0_2$
classes, weakly 2-random sets are not cototal.
To see that weak 2-randomness is optimal, we show that the
![]() $1$
-random Chaitin’s
$1$
-random Chaitin’s
![]() $\Omega $
is a cototal set.
$\Omega $
is a cototal set.
Theorem 3.2. There exists a 1-random cototal set.
Proof Because
![]() $\Omega $
is left-c.e., there is a non-descending computable sequence
$\Omega $
is left-c.e., there is a non-descending computable sequence
![]() $\lbrace q_n\rbrace $
of rationals such that
$\lbrace q_n\rbrace $
of rationals such that
![]() $\Omega =\lim _{n\rightarrow \infty }q_n$
. For any enumeration of
$\Omega =\lim _{n\rightarrow \infty }q_n$
. For any enumeration of
![]() $\overline {\Omega }$
, we can enumerate
$\overline {\Omega }$
, we can enumerate
![]() $\Omega $
using this computable sequence. First, to determine whether
$\Omega $
using this computable sequence. First, to determine whether
![]() $0$
is in
$0$
is in
![]() $\Omega $
or not, either for some n, we see the dyadic expansion of
$\Omega $
or not, either for some n, we see the dyadic expansion of
![]() $q_n$
starts with
$q_n$
starts with
![]() $1$
or we see
$1$
or we see
![]() $1$
enter
$1$
enter
![]() $\overline {\Omega }$
. Only for the first case, we enumerate
$\overline {\Omega }$
. Only for the first case, we enumerate
![]() $0$
in
$0$
in
![]() $\Omega $
. Then, we can iteratively do this process for each nature number in order. Eventually, we obtain an enumeration of
$\Omega $
. Then, we can iteratively do this process for each nature number in order. Eventually, we obtain an enumeration of
![]() $\Omega $
. Therefore,
$\Omega $
. Therefore,
![]() $\Omega \leq _e\overline {\Omega }$
.
$\Omega \leq _e\overline {\Omega }$
.
For the class of cototal e-degrees, we first discuss what level of randomness is enough to avoid them.
Theorem 3.3. Weakly 3-random sets do not have cototal e-degree.
Proof Notice that the class of cototal e-degrees defined by an enumeration operator
![]() $\Gamma _e$
is
$\Gamma _e$
is
 $$ \begin{align*} \lbrace A:A=\Gamma_e^{\overline{K_A}}\rbrace= \lbrace A:(\forall n) \lbrack & n\in A\rightarrow(\exists y)\lbrack\langle n,y\rangle\in\Gamma_e\rightarrow D_y\cap K_A=\emptyset\rbrack\\ \wedge & n\not\in A\rightarrow (\forall y)\lbrack \langle n,y\rangle\in\Gamma_e\rightarrow D_y\cap K_A\not=\emptyset\rbrack\rbrack\rbrace. \end{align*} $$
$$ \begin{align*} \lbrace A:A=\Gamma_e^{\overline{K_A}}\rbrace= \lbrace A:(\forall n) \lbrack & n\in A\rightarrow(\exists y)\lbrack\langle n,y\rangle\in\Gamma_e\rightarrow D_y\cap K_A=\emptyset\rbrack\\ \wedge & n\not\in A\rightarrow (\forall y)\lbrack \langle n,y\rangle\in\Gamma_e\rightarrow D_y\cap K_A\not=\emptyset\rbrack\rbrack\rbrace. \end{align*} $$
Since
![]() $D\cap K_A=\emptyset $
and
$D\cap K_A=\emptyset $
and
![]() $D\cap K_A\not =\emptyset $
are
$D\cap K_A\not =\emptyset $
are
![]() $\Pi ^0_1$
and
$\Pi ^0_1$
and
![]() $\Sigma ^0_1$
respectively, the class of cototal e-degrees defined by
$\Sigma ^0_1$
respectively, the class of cototal e-degrees defined by
![]() $\Gamma _e$
is
$\Gamma _e$
is
![]() $\Pi ^0_3$
. Since each of these classes is null, weakly 3-random sets avoid them all. So, we conclude that weakly 3-random sets do not have cototal e-degree.
$\Pi ^0_3$
. Since each of these classes is null, weakly 3-random sets avoid them all. So, we conclude that weakly 3-random sets do not have cototal e-degree.
Next, we see that weak 3-randomness is optimal by showing that there is a 2-random set of cototal e-degree even though any cototal set cannot be weakly 2-random.
Theorem 3.4. There exists a 2-random set of cototal e-degree.
Proof Consider Chaitin’s
![]() $\Omega $
relativized to
$\Omega $
relativized to
![]() $\emptyset '$
, i.e.,
$\emptyset '$
, i.e.,
![]() $\Omega ^{\emptyset '}$
, which is 2-random. Let L be
$\Omega ^{\emptyset '}$
, which is 2-random. Let L be
![]() $\lbrace q\in \mathbb {Q}_2: q<\Omega ^{\emptyset '}\rbrace $
. Then,
$\lbrace q\in \mathbb {Q}_2: q<\Omega ^{\emptyset '}\rbrace $
. Then,
![]() $L\leq _e\Omega ^{\emptyset '}\leq _e L\oplus \overline {L}$
. Notice that L is
$L\leq _e\Omega ^{\emptyset '}\leq _e L\oplus \overline {L}$
. Notice that L is
![]() $\Sigma _2^0$
. In [Reference Andrews, Ganchev, Kuyper, Lempp, Miller, Soskova and Soskova1], it was shown that every
$\Sigma _2^0$
. In [Reference Andrews, Ganchev, Kuyper, Lempp, Miller, Soskova and Soskova1], it was shown that every
![]() $\Sigma ^0_2$
set has cototal e-degree. So, there exists M such that
$\Sigma ^0_2$
set has cototal e-degree. So, there exists M such that
![]() ${M\equiv _e L}$
and
${M\equiv _e L}$
and
![]() $\overline {M}\geq _e M$
. Then,
$\overline {M}\geq _e M$
. Then,
![]() $\overline {\Omega ^{\emptyset '}\oplus L\oplus M}\geq _e\overline {L}\oplus \overline {M}\geq _e\overline {L}\oplus M\equiv _e\overline {L}\oplus L\geq _e\Omega ^{\emptyset '}\equiv _e\Omega ^{\emptyset '}\oplus L\oplus L\equiv _e\Omega ^{\emptyset '}\oplus L\oplus M$
. Hence, we have a cototal set that is enumeration equivalent to
$\overline {\Omega ^{\emptyset '}\oplus L\oplus M}\geq _e\overline {L}\oplus \overline {M}\geq _e\overline {L}\oplus M\equiv _e\overline {L}\oplus L\geq _e\Omega ^{\emptyset '}\equiv _e\Omega ^{\emptyset '}\oplus L\oplus L\equiv _e\Omega ^{\emptyset '}\oplus L\oplus M$
. Hence, we have a cototal set that is enumeration equivalent to
![]() $\Omega ^{\emptyset '}$
.
$\Omega ^{\emptyset '}$
.
In the proofs above, we did not use autoreducibility since it is enough to analyze the arithmetical complexities of the class of cototal sets and the class of cototal e-degrees to show the optimal level of randomness the sets in these classes must avoid. However, a similar analysis would not work for the classes of (uniform) introenumerable sets or e-degrees. We can verify the complexity of the collection of uniformly introenumerable e-degrees:
 $$ \begin{align*} \bigcup_e\lbrace A:\exists i,m\forall B & \lbrack\forall a \lbrack a\in A\leftrightarrow\exists b\lbrack\langle a,b\rangle\in\Gamma_m\wedge D_b\subseteq \Gamma_i(A)\rbrack\rbrack\wedge \\ & \lbrack B\subseteq\Gamma_i(A)\wedge\lbrack\forall p\in B\exists q>p \rbrack\rightarrow \\ \forall t & \lbrack t\in \Gamma_i(A)\leftrightarrow \exists s\lbrack \langle t,s\rangle\in\Gamma_e\wedge D_s\subseteq B\rbrack\rbrack\rbrack\rbrack\rbrace. \end{align*} $$
$$ \begin{align*} \bigcup_e\lbrace A:\exists i,m\forall B & \lbrack\forall a \lbrack a\in A\leftrightarrow\exists b\lbrack\langle a,b\rangle\in\Gamma_m\wedge D_b\subseteq \Gamma_i(A)\rbrack\rbrack\wedge \\ & \lbrack B\subseteq\Gamma_i(A)\wedge\lbrack\forall p\in B\exists q>p \rbrack\rightarrow \\ \forall t & \lbrack t\in \Gamma_i(A)\leftrightarrow \exists s\lbrack \langle t,s\rangle\in\Gamma_e\wedge D_s\subseteq B\rbrack\rbrack\rbrack\rbrack\rbrace. \end{align*} $$
This is
![]() $\Pi ^1_1$
. We suspect that the class of uniformly introenumerable e-degrees is
$\Pi ^1_1$
. We suspect that the class of uniformly introenumerable e-degrees is
![]() $\Pi ^1_1$
-complete. This was shown to be true for the class of uniformly introreducible sets in [Reference Greenberg, Harrison-Trainor, Patey and Turetsky6]. Assuming that there is no simpler definition, the analysis we used for cototal e-degrees would not work. Instead, for each set A of uniform introenumerable e-degree, we show
$\Pi ^1_1$
-complete. This was shown to be true for the class of uniformly introreducible sets in [Reference Greenberg, Harrison-Trainor, Patey and Turetsky6]. Assuming that there is no simpler definition, the analysis we used for cototal e-degrees would not work. Instead, for each set A of uniform introenumerable e-degree, we show
![]() $\Psi $
-autoreducibility for some autoreduction procedure
$\Psi $
-autoreducibility for some autoreduction procedure
![]() $\Psi $
so that we can apply Theorem 2.2 again.
$\Psi $
so that we can apply Theorem 2.2 again.
Theorem 3.5. Weakly 3-random sets do not have uniformly introenumerable e-degree.
Proof We will show that uniformly introenumerable e-degrees are contained in a countable union of measure zero
![]() $\Pi ^0_3$
classes. To do this, we show that each set A of uniformly introenumerable e-degree is
$\Pi ^0_3$
classes. To do this, we show that each set A of uniformly introenumerable e-degree is
![]() $\Psi $
-autoreducible for some
$\Psi $
-autoreducible for some
![]() $\Psi $
. Since A has uniformly introenumerable e-degree, there is a set B, enumeration operators
$\Psi $
. Since A has uniformly introenumerable e-degree, there is a set B, enumeration operators
![]() $\Phi $
,
$\Phi $
,
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $\Delta $
such that
$\Delta $
such that
![]() $A=\Delta (B),B=\Phi (A)$
, and for any infinite subset C of B,
$A=\Delta (B),B=\Phi (A)$
, and for any infinite subset C of B,
![]() $\Gamma (C)=B$
. Let
$\Gamma (C)=B$
. Let
 $$ \begin{align*}\Psi(n,Z)=\begin{cases} 1, & n\in\Delta(\Gamma(\Phi(Z))) \\ & \text{ or } \Phi(Z)\text{ is finite,}\\ 0, & \text{otherwise}. \end{cases}\end{align*} $$
$$ \begin{align*}\Psi(n,Z)=\begin{cases} 1, & n\in\Delta(\Gamma(\Phi(Z))) \\ & \text{ or } \Phi(Z)\text{ is finite,}\\ 0, & \text{otherwise}. \end{cases}\end{align*} $$
Note that n has to be in A when
![]() $\Phi (A-\lbrace n\rbrace )$
is finite. So, A is
$\Phi (A-\lbrace n\rbrace )$
is finite. So, A is
![]() $\Psi $
-autoreducible. Now we consider the class of
$\Psi $
-autoreducible. Now we consider the class of
![]() $\Psi $
-autoreducible sets:
$\Psi $
-autoreducible sets:
 $$ \begin{align*} \lbrace D:\forall n\lbrack & \lbrack n\in D\rightarrow n\in\Delta(\Gamma(\Phi(D-\lbrace n\rbrace)))\\ & \vee(\exists p\forall t>p) \lbrack t\not\in\Phi(D-\lbrace n\rbrace)\rbrack\rbrack\\ & \wedge \lbrack n\not\in D\rightarrow(\forall q\exists s>q)\lbrack s\in\Phi(D-\lbrace n\rbrace)\rbrack\\ & \wedge n\not\in\Delta(\Gamma(\Phi(D-\lbrace n\rbrace)))\rbrack\rbrack\rbrace. \end{align*} $$
$$ \begin{align*} \lbrace D:\forall n\lbrack & \lbrack n\in D\rightarrow n\in\Delta(\Gamma(\Phi(D-\lbrace n\rbrace)))\\ & \vee(\exists p\forall t>p) \lbrack t\not\in\Phi(D-\lbrace n\rbrace)\rbrack\rbrack\\ & \wedge \lbrack n\not\in D\rightarrow(\forall q\exists s>q)\lbrack s\in\Phi(D-\lbrace n\rbrace)\rbrack\\ & \wedge n\not\in\Delta(\Gamma(\Phi(D-\lbrace n\rbrace)))\rbrack\rbrack\rbrace. \end{align*} $$
This is a
![]() $\Pi ^0_3$
class. By Theorem 2.2, this is a null class. Because weakly 3-random sets cannot be in any
$\Pi ^0_3$
class. By Theorem 2.2, this is a null class. Because weakly 3-random sets cannot be in any
![]() $\Pi ^0_3$
null class, weakly 3-random sets do not have uniformly introenumerable e-degree.
$\Pi ^0_3$
null class, weakly 3-random sets do not have uniformly introenumerable e-degree.
Meanwhile, there also exists
![]() $2$
-random uniformly introenumerable e-degrees because of Theorem 3.4 and the fact that every set of cototal e-degree has uniform introenumerable e-degree.
$2$
-random uniformly introenumerable e-degrees because of Theorem 3.4 and the fact that every set of cototal e-degree has uniform introenumerable e-degree.
With more work, the previous result can be improved to show that weakly 3-random sets do not have introenumerable e-degree either.
Theorem 3.6. No weakly
![]() $3$
-random set has introenumerable e-degree.
$3$
-random set has introenumerable e-degree.
Proof Suppose a weakly 3-random set A has introenumerable e-degree. Let B be an introenumerable set such that there are enumeration operators
![]() $\Phi $
and
$\Phi $
and
![]() $\Delta $
with
$\Delta $
with
![]() $A=\Delta (B)$
and
$A=\Delta (B)$
and
![]() $B=\Phi (A)$
. For a contradiction, we define
$B=\Phi (A)$
. For a contradiction, we define
![]() $C=\bigcup _ic_i$
as an infinite subset of B such that
$C=\bigcup _ic_i$
as an infinite subset of B such that
![]() $\Gamma _i(C)\not =B$
for any enumeration operator
$\Gamma _i(C)\not =B$
for any enumeration operator
![]() $\Gamma _i$
(here we identified strings
$\Gamma _i$
(here we identified strings
![]() $c_i$
with corresponding sets). When we are constructing C, we also define a set
$c_i$
with corresponding sets). When we are constructing C, we also define a set
![]() $D_i$
at each stage i. Let
$D_i$
at each stage i. Let
![]() $c_0=\emptyset $
and
$c_0=\emptyset $
and
![]() $D_0=\emptyset $
. Suppose
$D_0=\emptyset $
. Suppose
![]() $c_i$
and
$c_i$
and
![]() $D_i$
have been defined. By inductive assumption,
$D_i$
have been defined. By inductive assumption,
![]() $\Phi (A-D_i)$
is infinite. First, we consider whether there is an extension e of
$\Phi (A-D_i)$
is infinite. First, we consider whether there is an extension e of
![]() $c_i$
such that
$c_i$
such that
![]() $e\preccurlyeq c_i\Phi (A-D_i)\upharpoonright \lbrack |c_i|,\infty )$
, and
$e\preccurlyeq c_i\Phi (A-D_i)\upharpoonright \lbrack |c_i|,\infty )$
, and
![]() $\Gamma _i(e)-B\not =\emptyset $
. If so, we define
$\Gamma _i(e)-B\not =\emptyset $
. If so, we define
![]() $c_{i+1}$
to be the least such e that contains at least one more element than
$c_{i+1}$
to be the least such e that contains at least one more element than
![]() $c_i$
and
$c_i$
and
![]() $D_{i+1}=D_i$
. If not, we consider whether there is an extension e of
$D_{i+1}=D_i$
. If not, we consider whether there is an extension e of
![]() $c_i$
such that for some n,
$c_i$
such that for some n,
![]() $\Phi (A-D_i\cup \lbrace n\rbrace )$
is infinite,
$\Phi (A-D_i\cup \lbrace n\rbrace )$
is infinite,
![]() $e\preccurlyeq c_i\Phi (A-D_i)\upharpoonright \lbrack |c_i|,\infty )$
, and
$e\preccurlyeq c_i\Phi (A-D_i)\upharpoonright \lbrack |c_i|,\infty )$
, and
![]() $\Gamma _i(e\Phi (A-D_i\cup \lbrace n\rbrace )\upharpoonright \lbrack |e|,\infty ))\subsetneq B$
. If so, we define
$\Gamma _i(e\Phi (A-D_i\cup \lbrace n\rbrace )\upharpoonright \lbrack |e|,\infty ))\subsetneq B$
. If so, we define
![]() $c_{i+1}$
to be the least such e that contains at least one more element than
$c_{i+1}$
to be the least such e that contains at least one more element than
![]() $c_i$
, and
$c_i$
, and
![]() $D_{i+1}=D_i\cup \lbrace n\rbrace $
. If not, we can define
$D_{i+1}=D_i\cup \lbrace n\rbrace $
. If not, we can define
 $$ \begin{align*}\Psi(n,Z)=\begin{cases} 1, & n\in\Delta(\Gamma_i(c_i\Phi(Z-D_i)\upharpoonright\lbrack|c_i|,\infty))) \\ & \text{ or } \Phi(Z-D_i)\text{ is finite,}\\ 0, & \text{otherwise,} \end{cases}\end{align*} $$
$$ \begin{align*}\Psi(n,Z)=\begin{cases} 1, & n\in\Delta(\Gamma_i(c_i\Phi(Z-D_i)\upharpoonright\lbrack|c_i|,\infty))) \\ & \text{ or } \Phi(Z-D_i)\text{ is finite,}\\ 0, & \text{otherwise,} \end{cases}\end{align*} $$
similar to the proof in Theorem 3.5. Notice that A is
![]() $\Psi $
-autoreducible and the class of
$\Psi $
-autoreducible and the class of
![]() $\Psi $
-autoreducible sets is
$\Psi $
-autoreducible sets is
![]() $\Pi ^0_3$
. This is impossible because A is weakly 3-random. This is a contradiction. Therefore, at least one of the two cases we considered has to be true. In this way, we obtain an infinite
$\Pi ^0_3$
. This is impossible because A is weakly 3-random. This is a contradiction. Therefore, at least one of the two cases we considered has to be true. In this way, we obtain an infinite
![]() $C=\bigcup _ic_i\subseteq B$
. Now we show that
$C=\bigcup _ic_i\subseteq B$
. Now we show that
![]() $\Gamma _i(C)\not =B$
for any i. For any i, if the first case we considered is true, then
$\Gamma _i(C)\not =B$
for any i. For any i, if the first case we considered is true, then
![]() $\Gamma _i(C)$
contains an element not in B. If the second case is true,
$\Gamma _i(C)$
contains an element not in B. If the second case is true,
![]() $\Gamma _i(C)\subseteq \Gamma _i(c_{i+1}\Phi (A-D_{i+1})\upharpoonright \lbrack |c_{i+1}|,\infty ))\subsetneq B$
.
$\Gamma _i(C)\subseteq \Gamma _i(c_{i+1}\Phi (A-D_{i+1})\upharpoonright \lbrack |c_{i+1}|,\infty ))\subsetneq B$
.
Again, by Theorems 1.6 and 3.4, we conclude that there exists
![]() $2$
-random introenumerable e-degree while there is no weakly
$2$
-random introenumerable e-degree while there is no weakly
![]() $3$
-random introenumerable e-degree. Next, we consider the class of uniformly introenumerable sets. We use the proof ideas of Proposition 8 given by Figueira, Miller, and Nies in [Reference Figueira, Miller and Nies3] that showed no random is autoreducible.
$3$
-random introenumerable e-degree. Next, we consider the class of uniformly introenumerable sets. We use the proof ideas of Proposition 8 given by Figueira, Miller, and Nies in [Reference Figueira, Miller and Nies3] that showed no random is autoreducible.
Theorem 3.7. No 1-random set is uniformly introenumerable.
Proof We will apply Schnorr’s theorem. To do so, we will show that the initial segment of any uniformly introenumerable set A can be compressed beyond any fixed constant.
Let
![]() $\Gamma $
be the enumeration operator such that
$\Gamma $
be the enumeration operator such that
![]() $\Gamma (B)=A$
for any infinite subset B of A. For each m, there is a least
$\Gamma (B)=A$
for any infinite subset B of A. For each m, there is a least
![]() $n_m$
such that
$n_m$
such that
![]() $n_m>n_p$
for any
$n_m>n_p$
for any
![]() $p<m$
and
$p<m$
and
![]() $\Gamma _{n_m}(0^mA\upharpoonright \lbrack m,n_m))\upharpoonright m=A\upharpoonright m$
since
$\Gamma _{n_m}(0^mA\upharpoonright \lbrack m,n_m))\upharpoonright m=A\upharpoonright m$
since
![]() $A-\lbrace 0,1,\dots ,m-1\rbrace $
is an infinite subset of A. Let
$A-\lbrace 0,1,\dots ,m-1\rbrace $
is an infinite subset of A. Let
![]() $c_m$
be the number of
$c_m$
be the number of
![]() $1$
’s in the string
$1$
’s in the string
![]() $A\upharpoonright m$
.
$A\upharpoonright m$
.
Now we define a prefix-free machine M that outputs
![]() $A\upharpoonright n_m$
with input
$A\upharpoonright n_m$
with input
![]() ${\gamma =0^{|\sigma |}1\sigma 0^{|\tau |}1\tau A\upharpoonright \lbrack m,n_m)}$
, where
${\gamma =0^{|\sigma |}1\sigma 0^{|\tau |}1\tau A\upharpoonright \lbrack m,n_m)}$
, where
![]() $\sigma ,\tau $
are binary strings corresponding to
$\sigma ,\tau $
are binary strings corresponding to
![]() $m,c_m$
. M first obtains the length of
$m,c_m$
. M first obtains the length of
![]() $\sigma $
by reading until the first
$\sigma $
by reading until the first
![]() $1$
and then obtains the number m by reading
$1$
and then obtains the number m by reading
![]() $|\sigma |$
many bits after the first
$|\sigma |$
many bits after the first
![]() $1$
. Next, M can find out
$1$
. Next, M can find out
![]() $c_m$
in the same way by reading the input until
$c_m$
in the same way by reading the input until
![]() $\tau $
. Now, M’s read head keeps on moving forward to read
$\tau $
. Now, M’s read head keeps on moving forward to read
![]() $A\upharpoonright \lbrack m,n_m)$
bit by bit to do the enumeration of
$A\upharpoonright \lbrack m,n_m)$
bit by bit to do the enumeration of
![]() $\Gamma (0^mA\upharpoonright \lbrack m,n_m))\upharpoonright m$
step by step to enumerate
$\Gamma (0^mA\upharpoonright \lbrack m,n_m))\upharpoonright m$
step by step to enumerate
![]() $A(x)$
for x between
$A(x)$
for x between
![]() $0$
and
$0$
and
![]() $m-1$
until
$m-1$
until
![]() $c_m$
many of such
$c_m$
many of such
![]() $A(x)$
is determined to be
$A(x)$
is determined to be
![]() $1$
, which means the other bits on
$1$
, which means the other bits on
![]() $A\upharpoonright m$
are zeros. M can output
$A\upharpoonright m$
are zeros. M can output
![]() $A\upharpoonright n_m$
by concatenation. Therefore,
$A\upharpoonright n_m$
by concatenation. Therefore,
![]() $K(A\upharpoonright n_m)\leq ^+ n_m-m+4\log (m)$
. By Schnorr’s theorem, A is not 1-random.
$K(A\upharpoonright n_m)\leq ^+ n_m-m+4\log (m)$
. By Schnorr’s theorem, A is not 1-random.
For introenumerable sets, we combine the methods used in Theorems 3.6 and 3.7.
Theorem 3.8. No 1-random set is introenumerable.
Proof Suppose there is a
![]() $1$
-random introenumerable set A. We prove the theorem by constructing an infinite subset
$1$
-random introenumerable set A. We prove the theorem by constructing an infinite subset
![]() $B=\bigcup _i b_i$
of A such that
$B=\bigcup _i b_i$
of A such that
![]() $\Gamma _i(B)\not =A$
for any enumeration operator
$\Gamma _i(B)\not =A$
for any enumeration operator
![]() $\Gamma _i$
(here we identified the strings
$\Gamma _i$
(here we identified the strings
![]() $b_i$
with its corresponding set).
$b_i$
with its corresponding set).
Let
![]() $b_0=\emptyset $
. Suppose we have already defined
$b_0=\emptyset $
. Suppose we have already defined
![]() $b_i$
. There are two possible cases. One of the two cases must hold for it to be
$b_i$
. There are two possible cases. One of the two cases must hold for it to be
![]() $1$
-random.
$1$
-random.
First, We consider whether there is an n such that
![]() $\Gamma _i(b_iA\upharpoonright \lbrack |b_i|,n))$
contains an element that is not in A. If so, we let
$\Gamma _i(b_iA\upharpoonright \lbrack |b_i|,n))$
contains an element that is not in A. If so, we let
![]() $b_{i+1}=b_iA\upharpoonright \lbrack |b_i|,n)$
. In this case, we have a finite extension
$b_{i+1}=b_iA\upharpoonright \lbrack |b_i|,n)$
. In this case, we have a finite extension
![]() $b_{i+1}$
of
$b_{i+1}$
of
![]() $b_i$
such that
$b_i$
such that
![]() $b_{i+1}$
is a subset of A, and for any infinite extension B of
$b_{i+1}$
is a subset of A, and for any infinite extension B of
![]() $b_{i+1}$
,
$b_{i+1}$
,
![]() $\Gamma _{i}(B)$
has an element not in A.
$\Gamma _{i}(B)$
has an element not in A.
Second, if there is no such n in the first case, we consider whether there is an m such that
![]() $\Gamma _i(b_i0^mA\upharpoonright \lbrack |b_i|+m,\infty ))\subsetneq A$
. If so, we let
$\Gamma _i(b_i0^mA\upharpoonright \lbrack |b_i|+m,\infty ))\subsetneq A$
. If so, we let
![]() $b_{i+1}=b_i0^m$
. In this case, we have a finite extension
$b_{i+1}=b_i0^m$
. In this case, we have a finite extension
![]() $b_{i+1}$
of
$b_{i+1}$
of
![]() $b_i$
such that applying
$b_i$
such that applying
![]() $\Gamma _i$
to A’s subset
$\Gamma _i$
to A’s subset
![]() $b_{i+1}A\upharpoonright \lbrack |b_{i+1}|,\infty )$
does not output A.
$b_{i+1}A\upharpoonright \lbrack |b_{i+1}|,\infty )$
does not output A.
If one of the cases holds for every i, we can show that for any i,
![]() $\Gamma _i(B)\not =A$
, contradicting introenumerability. If the first case holds for i, then for any extension
$\Gamma _i(B)\not =A$
, contradicting introenumerability. If the first case holds for i, then for any extension
![]() $B_0$
of
$B_0$
of
![]() $b_{i+1}$
,
$b_{i+1}$
,
![]() $\Gamma _i(B_0)\not =A$
. If the first case does not hold, notice that B is a subset of
$\Gamma _i(B_0)\not =A$
. If the first case does not hold, notice that B is a subset of
![]() $B_1=b_i0^mA\upharpoonright \lbrack |b_i|+m,\infty )$
. Then,
$B_1=b_i0^mA\upharpoonright \lbrack |b_i|+m,\infty )$
. Then,
![]() $\Gamma _i(B)\subseteq \Gamma _i(B_1)\subsetneq A$
.
$\Gamma _i(B)\subseteq \Gamma _i(B_1)\subsetneq A$
.
If neither cases hold for some i, we show that A is not
![]() $1$
-random using a method similar to the one used in the proof of the above theorem. For each m, there is a least
$1$
-random using a method similar to the one used in the proof of the above theorem. For each m, there is a least
![]() $n_m$
such that
$n_m$
such that
![]() $n_m>n_p$
for any
$n_m>n_p$
for any
![]() $p<m$
and
$p<m$
and
because the failure of the second case guarantees that eventually numbers in
![]() $A\upharpoonright |b_i|+m$
will be enumerated and no other numbers would be enumerated by the failure of the first case. Let
$A\upharpoonright |b_i|+m$
will be enumerated and no other numbers would be enumerated by the failure of the first case. Let
![]() $c_m$
be the number of
$c_m$
be the number of
![]() $1$
s in the string
$1$
s in the string
![]() $A\upharpoonright \lbrack |b_i|,|b_i|+m)$
. Now we define a prefix-free machine M that outputs
$A\upharpoonright \lbrack |b_i|,|b_i|+m)$
. Now we define a prefix-free machine M that outputs
![]() $A\upharpoonright n_m$
with input
$A\upharpoonright n_m$
with input
![]() $\gamma =0^{|\sigma |}1\sigma 0^{|\tau |}1\tau A\upharpoonright \lbrack |b_i|+m,n_m)$
, where
$\gamma =0^{|\sigma |}1\sigma 0^{|\tau |}1\tau A\upharpoonright \lbrack |b_i|+m,n_m)$
, where
![]() $\sigma ,\tau $
are binary strings corresponding to
$\sigma ,\tau $
are binary strings corresponding to
![]() $m,c_m$
. M obtains
$m,c_m$
. M obtains
![]() $m,c_m$
in the same way as the proof above by reading until
$m,c_m$
in the same way as the proof above by reading until
![]() $\tau $
. Then, M obtains the first
$\tau $
. Then, M obtains the first
![]() $|b_i|$
bits of A using
$|b_i|$
bits of A using
![]() $\Gamma _i$
. Next, its read head keeps on moving forward to read
$\Gamma _i$
. Next, its read head keeps on moving forward to read
![]() $A\upharpoonright \lbrack |b_i|+m,n_m)$
bit by bit to do the enumeration of
$A\upharpoonright \lbrack |b_i|+m,n_m)$
bit by bit to do the enumeration of
![]() $\Gamma _i(b_i0^mA\upharpoonright \lbrack |b_i|+m,n_m))$
step by step to enumerate
$\Gamma _i(b_i0^mA\upharpoonright \lbrack |b_i|+m,n_m))$
step by step to enumerate
![]() $A(x)$
for x between
$A(x)$
for x between
![]() $|b_i|$
and
$|b_i|$
and
![]() $|b_i|+m-1$
until
$|b_i|+m-1$
until
![]() $c_m$
many of such
$c_m$
many of such
![]() $A(x)$
is determined to be
$A(x)$
is determined to be
![]() $1$
and output
$1$
and output
![]() $A\upharpoonright n_m$
by concatenation. Therefore,
$A\upharpoonright n_m$
by concatenation. Therefore,
![]() $K(A\upharpoonright n_m)\leq ^+ n_m-m+4\log (m)$
. By Schnorr’s theorem, A is not 1-random.
$K(A\upharpoonright n_m)\leq ^+ n_m-m+4\log (m)$
. By Schnorr’s theorem, A is not 1-random.