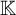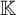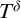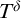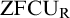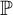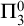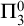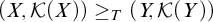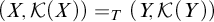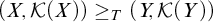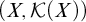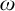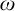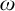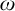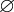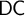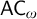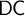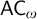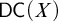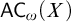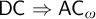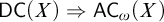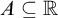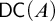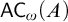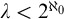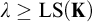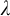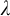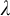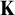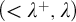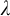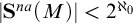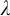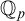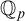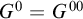FirstView articles
Article
A NOTE ON THE STRONG ERDŐS–HAJNAL PROPERTY FOR GRAPHS WITH BOUNDED VC-MINIMAL COMPLEXITY
- Part of:
-
- Published online by Cambridge University Press:
- 15 November 2024, pp. 1-7
-
- Article
-
- You have access
- HTML
- Export citation
GENERIC DERIVATIONS ON ALGEBRAICALLY BOUNDED STRUCTURES
- Part of:
-
- Published online by Cambridge University Press:
- 13 November 2024, pp. 1-27
-
- Article
-
- You have access
- HTML
- Export citation
AXIOMATIZATION AND FORCING IN SET THEORY WITH URELEMENTS
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2024, pp. 1-27
-
- Article
-
- You have access
- HTML
- Export citation
BOREL LINE GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
THE GROUP CONFIGURATION THEOREM FOR GENERICALLY STABLE TYPES
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2024, pp. 1-44
-
- Article
-
- You have access
- HTML
- Export citation
COUNTABLE SPACES, REALCOMPACTNESS, AND THE PSEUDOINTERSECTION NUMBER
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2024, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTERNAL AUTOMORPHISMS AND ANTIMORPHISMS OF MODELS OF NF
-
- Published online by Cambridge University Press:
- 29 October 2024, pp. 1-5
-
- Article
-
- You have access
- HTML
- Export citation
A RECURSIVE COLORING FUNCTION WITHOUT
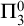 $ \Pi _3^0$ SOLUTIONS FOR HINDMAN’S THEOREM
$ \Pi _3^0$ SOLUTIONS FOR HINDMAN’S THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2024, pp. 1-24
-
- Article
-
- You have access
- HTML
- Export citation
THE SHAPE OF COMPACT COVERS
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2024, pp. 1-15
-
- Article
-
- You have access
- HTML
- Export citation
STRICTLY n-FINITE VARIETIES OF HEYTING ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2024, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A PARAMETERIZED HALTING PROBLEM,
 $ \Delta _0$ TRUTH AND THE MRDP THEOREM
$ \Delta _0$ TRUTH AND THE MRDP THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1-26
-
- Article
-
- You have access
- HTML
- Export citation
ARTIN–SCHREIER EXTENSIONS AND COMBINATORIAL COMPLEXITY IN HENSELIAN VALUED FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 03 September 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation
LIMIT COMPLEXITIES, MINIMAL DESCRIPTIONS, AND n-RANDOMNESS
- Part of:
-
- Published online by Cambridge University Press:
- 05 June 2024, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DIAMOND ON LADDER SYSTEMS AND COUNTABLY METACOMPACT TOPOLOGICAL SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INVARIANT KEISLER MEASURES FOR
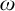 $\omega $-CATEGORICAL STRUCTURES
$\omega $-CATEGORICAL STRUCTURES
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON AUTOMORPHISMS OF
 ${\mathcal {P}}(\lambda )/[\lambda ]^{<\lambda }$
${\mathcal {P}}(\lambda )/[\lambda ]^{<\lambda }$
- Part of:
-
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DOES
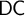 $\mathsf {DC}$ IMPLY
$\mathsf {DC}$ IMPLY 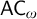 ${\mathsf {AC}}_\omega $, UNIFORMLY?
${\mathsf {AC}}_\omega $, UNIFORMLY?
- Part of:
-
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1-25
-
- Article
-
- You have access
- HTML
- Export citation
BUILDING MODELS IN SMALL CARDINALS IN LOCAL ABSTRACT ELEMENTARY CLASSES
- Part of:
-
- Published online by Cambridge University Press:
- 29 April 2024, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ONE-DIMENSIONAL SUBGROUPS AND CONNECTED COMPONENTS IN NON-ABELIAN p-ADIC DEFINABLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 29 April 2024, pp. 1-19
-
- Article
-
- You have access
- HTML
- Export citation
GENERIC EXPANSIONS OF GEOMETRIC THEORIES
- Part of:
-
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation