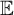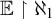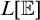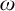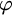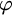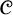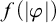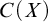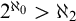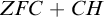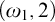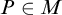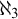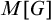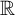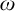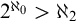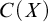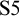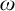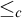Article
THE DEFINABILITY OF THE EXTENDER SEQUENCE
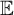 $\mathbb {E}$ FROM
$\mathbb {E}$ FROM 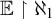 $\mathbb {E}\upharpoonright \aleph _1$ IN
$\mathbb {E}\upharpoonright \aleph _1$ IN 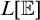 $L[\mathbb {E}]$
$L[\mathbb {E}]$
- Part of:
-
- Published online by Cambridge University Press:
- 15 April 2024, pp. 427-459
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CLASSIFICATION OF
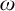 $\omega $-CATEGORICAL MONADICALLY STABLE STRUCTURES
$\omega $-CATEGORICAL MONADICALLY STABLE STRUCTURES
- Part of:
-
- Published online by Cambridge University Press:
- 19 September 2023, pp. 460-495
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MORE ON GALOIS COHOMOLOGY, DEFINABILITY, AND DIFFERENTIAL ALGEBRAIC GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2024, pp. 496-515
-
- Article
- Export citation
FORBIDDEN INDUCED SUBGRAPHS AND THE ŁOŚ–TARSKI THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2024, pp. 516-548
-
- Article
- Export citation
PARTITIONING THE REAL LINE INTO BOREL SETS
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2023, pp. 549-568
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE COFINALITY OF THE LEAST
 $\lambda $-STRONGLY COMPACT CARDINAL
$\lambda $-STRONGLY COMPACT CARDINAL
- Part of:
-
- Published online by Cambridge University Press:
- 19 January 2023, pp. 569-582
-
- Article
- Export citation
MODULAR MANY-VALUED SEMANTICS FOR COMBINED LOGICS
- Part of:
-
- Published online by Cambridge University Press:
- 20 April 2023, pp. 583-636
-
- Article
- Export citation
CANTORIAN MODELS OF PREDICATIVE
 $\mathrm {NF}$
$\mathrm {NF}$
- Part of:
-
- Published online by Cambridge University Press:
- 13 October 2022, pp. 637-645
-
- Article
- Export citation
ISOMORPHISM OF LOCALLY COMPACT POLISH METRIC STRUCTURES
- Part of:
-
- Published online by Cambridge University Press:
- 19 December 2022, pp. 646-664
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DISCONTINUOUS HOMOMORPHISMS OF
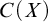 $C(X)$ WITH
$C(X)$ WITH 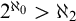 $2^{\aleph _0}>\aleph _2$
$2^{\aleph _0}>\aleph _2$
- Part of:
-
- Published online by Cambridge University Press:
- 15 April 2024, pp. 665-696
-
- Article
- Export citation
TIGHT EVENTUALLY DIFFERENT FAMILIES
- Part of:
-
- Published online by Cambridge University Press:
- 02 March 2023, pp. 697-723
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NSOP
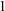 $_1$-LIKE INDEPENDENCE IN AECATS
$_1$-LIKE INDEPENDENCE IN AECATS
- Part of:
-
- Published online by Cambridge University Press:
- 12 December 2022, pp. 724-757
-
- Article
- Export citation
AXIOMATIZABILITY OF PROPOSITIONALLY QUANTIFIED MODAL LOGICS ON RELATIONAL FRAMES
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2022, pp. 758-793
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KATĚTOV ORDER ON MAD FAMILIES
- Part of:
-
- Published online by Cambridge University Press:
- 24 April 2023, pp. 794-828
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PARTITION GENERICITY AND PIGEONHOLE BASIS THEOREMS
- Part of:
-
- Published online by Cambridge University Press:
- 03 October 2022, pp. 829-857
-
- Article
- Export citation
ON COHEN AND PRIKRY FORCING NOTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 11 September 2023, pp. 858-904
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KEISLER’S THEOREM AND CARDINAL INVARIANTS
-
- Published online by Cambridge University Press:
- 18 November 2022, pp. 905-917
-
- Article
- Export citation
INVESTIGATING THE COMPUTABLE FRIEDMAN–STANLEY JUMP
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2023, pp. 918-944
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
JSL volume 89 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 21 May 2024, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
JSL volume 89 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 21 May 2024, pp. b1-b2
-
- Article
-
- You have access
- Export citation