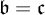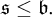KATĚTOV ORDER ON MAD FAMILIES

OSVALDO GUZMÁN

doi:10.1017/jsl.2023.25

KATĚTOV ORDER ON MAD FAMILIES

Part of: Set theory

Published online by Cambridge University Press: 24 April 2023

OSVALDO GUZMÁN

Show author details

OSVALDO GUZMÁN*: Affiliation:
CENTRO DE CIENCIAS MATEMÁTICAS UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO MORELIA, MEXICO
*: E-mail: oguzman@matmor.unam.mx

Article contents

Abstract
Introduction
Notation
Preliminaries
Katětov-top MAD families vs. $\mathfrak {s\leq b}$
A Katětov maximal MAD family from $\mathfrak {b=c}$
Two more constructions
The Cohen model
Open questions
Funding
Footnotes
References

Rights & Permissions

Abstract

We continue with the study of the Katětov order on MAD families. We prove that Katětov maximal MAD families exist under $\mathfrak {b=c}$ and that there are no Katětov-top MAD families assuming $\mathfrak {s\leq b}.$ This improves previously known results from the literature. We also answer a problem form Arciga, Hrušák, and Martínez regarding Katětov maximal MAD families.

Keywords

Katětov order MAD families Cohen forcing

MSC classification

Primary: 03E17: Cardinal characteristics of the continuum 03E05: Other combinatorial set theory 03E35: Consistency and independence results

Type: Article
Information: The Journal of Symbolic Logic , Volume 89 , Issue 2 , June 2024 , pp. 794 - 828

DOI: https://doi.org/10.1017/jsl.2023.25 [Opens in a new window]
Creative Commons: This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright: © The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

1 Introduction

Ideals on countable setsFootnote ¹ play a fundamental role in infinite combinatorics. It is for this reason that there is desire to have ways to classify and study them. In [Reference Katětov49] Katětov introduced the following (pre)order:

Definition 1. Let $X$ and Y be two countable sets, $\ \mathcal {I},\mathcal {J}$ ideals on X and Y, respectively, and $f:Y\longrightarrow X$ .

1. f is a Katětov function from $\left ( Y,\mathcal {J}\right ) $ to $\left ( X,\mathcal {I}\right ) $ if $f^{-1}\left ( A\right ) \in \mathcal {J}$ for every $A\in \mathcal {I}.$
2. $\mathcal {I}\leq _{\textsf {K}}\mathcal {J}$ ( $\mathcal {I}$ is Katětov smaller that $\mathcal {J}$ or $\mathcal {J}$ is Katětov above $\mathcal {I}$ ) if there is a Katětov function from $\left ( Y,\mathcal {J} \right ) $ to $\left ( X,\mathcal {I}\right ) .$
3. $\mathcal {I}=_{\textsf {K}}\mathcal {J}$ ( $\mathcal {I}$ is Katětov equivalent to $\mathcal {J}$ ) if $\mathcal {I\leq _{\textsf {K} }J}$ and $\mathcal {J\leq _{\textsf {K}}I}.$

The Katětov order is a powerful tool for studying ideals over countable sets. We will briefly mention two reasons why this is the case (for more information and motivation, the reader may consult [Reference Hrušák37, Reference Hrušák39]). With the Katětov order, it is possible to classify non-definable objects (like MAD families and ultrafilters) using Borel ideals. Almost all of the most interesting properties of ultrafilters can be reformulated in terms of the Katětov order. For example, an ultrafilter $\mathcal {U}$ is a Ramsey ultrafilter if and only if its dual $\mathcal {U}^{\ast }$ is not Katětov above the ideal $\mathcal {ED}, \mathcal {U}$ is a P-point if and only if $\mathcal {U}^{\ast }$ is not Katětov above fin $\times $ fin and $\mathcal {U}$ is a nowhere dense ultrafilter if and only if $\mathcal {U}$ is not Katětov above the ideal nwd (for more information, see [Reference Brendle and Flašková6, Reference Hrušák39]).

Let X be a set, $\mathcal {I}$ an ideal on X and $\mathbb {P}$ a partial order. We say that $\mathbb {P}$ destroys $\mathcal {I}$ if $\mathbb {P}$ adds a an infinite subset of X that is almost disjoint with every element of $\mathcal {I}.$ This notion is interesting since the theory of destructibility of ideals is very important in forcing. Mainly, many important forcing properties can be stated in these terms. For example, a partial order $\mathbb {P}$ adds dominating reals if and only if $\mathbb {P}$ destroys fin $\times $ fin or $\mathbb {P}$ adds eventually different reals if and only if $\mathbb {P}$ destroys $\mathcal {ED}.$ It is not hard to prove that if $\mathcal {I}$ and $\mathcal {J}$ are two ideals such that $\mathcal {I\leq _{\textsf {K}}J}$ and $\mathbb {P}$ destroys $\mathcal {J},$ then $\mathbb {P}$ will also destroy $\mathcal {I}$ (see [Reference Hrušák and Ferreira40]). In this way, the Katětov order helps us understand which ideals are destroyed after performing a forcing extension. Furthermore, the ideals destroyed by Cohen forcing are precisely those ideals that are Katětov below the ideal of the nowhere dense subsets of the rational numbers (there are also similar results for Random, Sacks, Laver, and Miller forcings (see [Reference Brendle and Yatabe9, Reference Hrušák and Zapletal44] for more information and related results)).

The Katětov order is related to the Rudin–Keisler order, which we recall now:

Definition 2. Let $X$ and Y be two countable sets, $\ \mathcal {I},\mathcal {J}$ ideals on X and Y, respectively, and $f:Y\longrightarrow X$ .

1. f is a Rudin–Keisler function from $\left ( Y,\mathcal {J} \right ) $ to $\left ( X,\mathcal {I}\right ) $ if for every $A\subseteq X,$ we have that $f^{-1}\left ( A\right ) \in \mathcal {J}$ if and only if $A\in \mathcal {I}.$
2. $\mathcal {I\leq _{\textsf {RK}}J}$ ( $\mathcal {I}$ is Rudin–Keisler smaller that $\mathcal {J}$ ) if there is a Rudin–Keisler function from $\left ( Y,\mathcal {J}\right ) $ to $\left ( X,\mathcal {I}\right ) .$

It is not hard to see that if $\mathcal {U}$ and $\mathcal {V}$ are ultrafilters, then $\mathcal {U}^{\ast } \leq _{\textsf {K}} \mathcal {V}^{\ast }$ if and only if $\mathcal {U}^{\ast } \leq _{\textsf {RK}}\mathcal {V}^{\ast }.$ The Rudin–Keisler order on ultrafilters (or equivalently, on its duals) has been extensively studied in the past (see [Reference Goldbring27, Reference Halbeisen34, Reference Jech46]). It is interesting that the theory of MAD families under the Katětov order, mirrors the one of ultrafilters. The ideals generated by MAD families are coinitial in the Katětov order, while the duals of ultrafilters are cofinal. Let $\mathcal {U}$ be an ultrafilter. In an informal sense, the lower $\mathcal {U}^{\ast }$ is in the Katětov order, the more interesting $\mathcal {U}$ is. Dually, the higher a MAD family is in the Katětov order, the more interesting it is. We expect that the theory of MAD families under the Katětov order will be as rich and interesting as the one of ultrafilters.

The following result is well known (for a proof, the reader may consult [Reference Goldbring27, Reference Halbeisen34, Reference Jech46]).

Proposition 3. Let $\mathcal {U}$ be an ultrafilter. The following are equivalent $:$

1. $\mathcal {U}$ is Ramsey.
2. If $\mathcal {W}$ is an ultrafilter such that $\mathcal {W} ^{\ast } \leq _{\textsf {K}}\mathcal {U}^{\ast },$ then $\mathcal {U}^{\ast } \leq _{\textsf {K}}\mathcal {W}^{\ast }$ (so $\mathcal {U}^{\ast }$ and $\mathcal {W}^{\ast }$ are Katětov equivalent).

In other words, Ramsey ultrafilters are the ultrafilters whose dual is Katětov minimal. Ramsey ultrafilters are very important in Set Theory. It might be interesting to look at the analogue for MAD families.Footnote ² Given a MAD family $\mathcal {A},$ by $\mathcal {I(A)}$ we denote the ideal generated by $\mathcal {A}$ (and finite sets).

Definition 4. Let $\mathcal {A}$ be a MAD family. We say that $\mathcal {A}$ is Katětov maximal if for every MAD family $\mathcal {B},$ if $\mathcal {I(A)} \leq _{\textsf {K}}\mathcal {I}\left ( \mathcal {B} \right ) ,$ then $\mathcal {I(A)} =_{\textsf {K}}\mathcal {I}\left ( \mathcal {B}\right ) $ .

This notion was first consider by García-Ferreira and Hrušák in [Reference Hrušák and Ferreira40]. However, it remained an open problem if such families could exist. This problem was finally answered in [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1] by Arciga, Hrušák, and Martínez:

Theorem 5 (Arciga, Hrušák, and Martínez [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1]).

$\mathfrak {t=c}$ implies that there is a Katětov maximal MAD family.

We will improve the theorem above. In Section 5, we will prove that $\mathfrak {b=c}$ is enough to build a Katětov maximal MAD family. In Section 6, we will construct Katětov maximal MAD families with additional properties and answer a question of Arciga, Hrušák, and Martínez. It is currently unknown if ZFC proves that there is a Katětov maximal MAD family. In Section 7, we study the Cohen model. We will prove that there is no Katětov maximal MAD family of size $\omega _{1}$ in the Cohen model. It is worth pointing out that MAD families of size $\omega _{1}$ do exist in the model (see [Reference Kunen50]).

We now turn our attention to an even stronger property than maximality. This property was also studied by García-Ferreira and Hrušák in [Reference Hrušák and Ferreira40].

Definition 6. Let $\mathcal {A}$ be a MAD family. We say that $\mathcal {A}$ is Katětov-top if $\mathcal {I(B)} \leq _{\textsf {K}} \mathcal {I}(\mathcal {A})$ for every MAD family $\mathcal {B}.$

Contrary to Katětov maximal MAD families, one would expect that Katětov-top MAD families do not exist. In [Reference Hrušák and Ferreira40] the following partial result was obtained:

Theorem 7 (García-Ferreira and Hrušák [Reference Hrušák and Ferreira40]).

$\mathfrak {b=c}$ implies that there are no Katětov-top MAD families.

We will improve this theorem and show that there are no such families under $\mathfrak {s\leq b}$ . It is still unknown if ZFC proves that Katětov-top MAD families do not exist. We include some discussion of this in Section 4.

2 Notation

A family $\mathcal {A}\subseteq \left [ \omega \right ] ^{\omega }$ is almost disjoint (AD) if the intersection of any two different elements of $\mathcal {A}$ is finite, a MAD family is a maximal almost disjoint family. To avoid trivial considerations, we always assume MAD families to be infinite.

Given a set $X,$ by $\mathcal {P}\left ( X\right ) $ we denote the power set of $X.$ Let f be a function. By dom $\left ( f\right ) $ we denote the domain of X and by img $\left ( f\right ) $ we denote its image. We say f is a partial function from X to Y (where X and Y are two sets) if dom $\left ( f\right ) \subseteq X$ and img $\left ( f\right ) \subseteq Y.$ This will be denoted by f $;X\longrightarrow Y.$ Given $A\subseteq X,$ by $f\left [ A\right ] $ we denote $f\left [ A\cap {\textsf {dom}}\left ( f\right ) \right ] .$

Definition 8. Let X be a set.

1. We say that $\mathcal {F\subseteq } \wp \left ( X\right ) $ is a filter on X if the following conditions hold $:$
1. (a) $X\in \mathcal {F}$ and $\emptyset \notin \mathcal {F}.$
2. (b) If $A\in \mathcal {F}$ and $A\subseteq B$ then $B\in \mathcal {F}.$
3. (c) If $A,B\in \mathcal {F}$ then $A\cap B\in \mathcal {F}.$
2. We say that $\mathcal {I\subseteq } \wp \left ( X\right ) $ is an ideal on X if the following conditions hold $:$
1. (a) Every finite subset of X is in $\mathcal {I}.$
2. (b) If $A\in \mathcal {I}$ and $B\subseteq A$ then $B\in \mathcal {I}.$
3. (c) If $A,B\in \mathcal {I}$ then $A\cup B\in \mathcal {I}.$

We will be mainly interested in filters and ideals on countable sets. An ideal $\mathcal {I\subseteq } \wp \left ( X\right ) $ is a proper ideal if $X\notin \mathcal {I},$ otherwise it is called an improper ideal. We say that $\mathcal {I}$ is tall if for every infinite $A\subseteq X,$ there is $I\in \mathcal {I}$ such that $A\cap I$ is infinite. By fin we denote the ideal of finite subsets of $\omega .$

Definition 9. Let $\mathcal {A}$ be an AD family on $\omega .$

1. $\mathcal {I}\left ( \mathcal {A}\right ) $ is the ideal generated by $\mathcal {A}.$ In other words, $X\in \mathcal {I}\left ( \mathcal {A}\right ) $ if and only if there are $A_{0},\dots ,A_{n}\in \mathcal {A}$ and s a finite set such that $X\subseteq A_{0}\cup \dots \cup A_{n}\cup s.$
2. $\mathcal {I}\left ( \mathcal {A}\right ) ^{+}$ is the collection of all subsets of $\omega $ that are not in $\mathcal {I}\left ( \mathcal {A}\right ) .$
3. $\mathcal {I}\left ( \mathcal {A}\right ) ^{++}$ is the set of all $X\subseteq \omega $ for which there is $\mathcal {B\in } \left [ \mathcal {A} \right ] ^{\omega }$ such that if $A\in \mathcal {B}$ then $X\cap A$ is infinite.
4. $\mathcal {A}^{\perp }$ is the set of all $X\subseteq \omega $ such that $\left \vert X\cap A\right \vert <\omega $ for every $A\in \mathcal {A}.$
5. Let $X\in \left [ \omega \right ] ^{\omega }.$ Define $\mathcal {A} \upharpoonright X=\left \{ A\cap X\mid A\in \mathcal {A}\right \} \setminus \left [ \omega \right ] ^{<\omega }.$
6. We say $\mathcal {A}$ is nowhere MAD if for every $X\in \mathcal {I}\left ( \mathcal {A}\right ) ^{+},$ there is $Y\in \left [ X\right ] ^{\omega }$ such that $Y\in \mathcal {A}^{\perp }.$ In other words, $\mathcal {A} \upharpoonright X$ is not maximal in $X.$

The cardinal invariants of the continuum play a leading role in this paper. We list the cardinal invariants that will be needed. The reader can learn about cardinal invariants in [Reference Blass4]. In almost all instances in the paper, the expression “almost all” means that the set of exceptions is finite.

1. The almost disjointness number $\mathfrak {a}$ is the smallest size of a MAD family.
2. The size of the continuum is denoted by $\mathfrak {c}.$
3. Let $f,g\in \omega ^{\omega }.$ By $f\leq ^{\ast }g$ we mean that $f\left ( n\right ) \leq g\left ( n\right ) $ holds for almost all $n\in \omega .$ The expression $f\leq _{n}g$ means that if $m\geq n,$ then $f\left ( m\right ) \leq g\left ( m\right ) .$
4. The bounding number $\mathfrak {b}$ is the smallest size of an unbounded family of functions (with respect to the $\leq ^{\ast }$ ordering).
5. Let $A,B\in \left [ \omega \right ] ^{\omega }.$ The expression $A\subseteq ^{\ast }B$ means that $A\setminus B$ is finite. In this case, we say that A is almost contained in $B.$
6. Let $\mathcal {H}\subseteq \left [ \omega \right ] ^{\omega }.$ We say that $\mathcal {H}$ is centered if for every $n\in \omega $ and $A_{0} ,\dots ,A_{n}\in \mathcal {H},$ it is the case that $A_{0}\cap \dots \cap A_{n}$ is infinite. We say that $P\in \left [ \omega \right ] ^{\omega }$ is a pseudointersection of $\mathcal {H}$ if P is almost contained in every member of $\mathcal {H}.$
7. The pseudointersection number $\mathfrak {p}$ is the smallest size of a centered family with no infinite pseudointersection.
8. A family $\mathcal {H}=\left \{ A_{\alpha }\mid \alpha <\kappa \right \} \subseteq \left [ \omega \right ] ^{\omega }$ is a tower if $A_{\alpha }\subseteq ^{\ast }A_{\beta }$ whenever $\alpha>\beta $ and $\mathcal {H}$ has no infinite pseudointersections.
9. The tower number $\mathfrak {t}$ is the smallest size of a tower.
10. Let $\mathcal {D} \subseteq \left [ \omega \right ] ^{\omega }.$ We say that $\mathcal {D}$ is dense in $\left [ \omega \right ] ^{\omega }$ if for every $A\in \left [ \omega \right ] ^{\omega }$ there is $B\in \mathcal {D}$ such that $B\subseteq ^{\ast }A.$ We say $\mathcal {D}$ is open in $\left [ \omega \right ] ^{\omega }$ if for every $A\in \mathcal {D},$ if $B\subseteq ^{\ast }A,$ then $B\in \mathcal {D}.$ We say that $\mathcal {D}$ is open dense in $\left [ \omega \right ] ^{\omega }$ if it is both open and dense in $\left [ \omega \right ] ^{\omega }.$
11. The distributivity number $\mathfrak {h}$ is the smallest size of a family of open dense sets in $\left [ \omega \right ] ^{\omega }$ with empty intersection.
12. The uniformity of the meager ideal non $\left ( \mathcal {M}\right ) $ is the smallest size of a nonmeager subset of the Baire space $\omega ^{\omega }.$

A celebrated theorem of Malliaris and Shelah is that $\mathfrak {p}$ and $\mathfrak {t}$ are equal (see [Reference Malliaris and Shelah53]). Since we will be referencing theorems in papers that were written before it was proved that these two cardinal invariants are the same, we will be writing $\mathfrak {p}$ or $\mathfrak {t}$ depending on how it was written in the cited paper. It is well-known that $\mathfrak {p\leq h\leq b\leq a\leq c}$ and $\mathfrak {b\leq }$ non $\left ( \mathcal {M}\right ) \leq \mathfrak {c}$ (the proofs of these inequalities can be consulted in [Reference Blass4]). There is no provable relation between non $\left ( \mathcal {M}\right ) $ and $\mathfrak {a},$ although it is an open question if non $\left ( \mathcal {M}\right ) =\omega _{1}$ implies that $\mathfrak {a}=\omega _{1}.$

By $\omega ^{<\omega \nearrow }$ we denote the set of all finite increasing sequences of $\omega .$ Given $A\in \left [ \omega \right ] ^{\omega },$ its enumerating function is the unique increasing bijection between $\omega $ and $A.$ By identifying each set with its characteristic function, we can view ideals or filters on $\omega $ as subspaces of the Cantor space $2^{\omega }.$ In this way, we can say when an ideal is Borel or analytic. By fin we denote the ideal of finite subsets of $\omega $ and nwddenotes the ideal of nowhere dense subsets of the rational numbers.

3 Preliminaries

In this section, we will recall some properties of the Katětov order and AD families. Nothing in this section is really new, but we will take the opportunity to state explicitly some lemmas that only appear implicitly in the literature. We only provide proofs of the statements that (to the best of our knowledge) have not been explicitly proved elsewhere.

For convenience, if $\mathcal {A}$ is an AD family and $\mathcal {J}$ an ideal, we will write $\mathcal {A}\leq _{\textsf {K}}\mathcal {J}$ ( $\mathcal {J}\leq _{\textsf {K}}\mathcal {A}$ ) instead of $\mathcal {I(A)} \leq _{\textsf {K}}\mathcal {J}$ ( $\mathcal {J}\leq _{\textsf {K}} \mathcal {I(A)}$ ). We start recalling the most basic remarks about the Katětov order (see [Reference Hrušák and Ferreira40] for a proof):

Lemma 10. Let $\mathcal {I},\mathcal {J},\mathcal {L}$ be ideals and $\mathcal {A} ,\mathcal {B}$ two AD families.

1. $\mathcal {I=_{\textsf {K}}I}.$
2. If $\mathcal {I\leq _{\textsf {K}}J}$ and $\mathcal {J\leq _{\textsf {K}}L},$ then $\mathcal {I\leq _{\textsf {K}}L}.$
3. fin is the smallest element in the Katětov order.
4. $\mathcal {I}$ is Katětov equivalent to fin if and only if $\mathcal {I}$ is not tall.
5. $\mathcal {A}$ is MAD if and only if $\mathcal {A}\nleq _{\textsf {K}}$ fin.
6. If $X\in \mathcal {I}\left ( \mathcal {A}\right ) ^{+},$ then $\mathcal {A}\leq _{\textsf {K}} \mathcal {A}\upharpoonright X.$
7. If $\mathcal {A}\leq _{\textsf {K}} \mathcal {B},$ then $\left \vert \mathcal {B}\right \vert \leq \left \vert \mathcal {A}\right \vert .$

The following is a useful reformulation of the Katětov order:

Lemma 11. Let $X,Y$ countable sets, $\mathcal {I}$ an ideal on $X, \mathcal {J}$ an ideal on Y and $f:X\longrightarrow Y.$ The following are equivalent $:$

1. f is a Katětov function from $(X,\mathcal {I})$ to $(Y,\mathcal {J} ).$
2. If $A\in \mathcal {I}^{+},$ then $f\left [ A\right ] \in \mathcal {J}^{+}.$

Proof We first prove that the first point implies the second. Assume f is a Katětov function from $(X,\mathcal {I})$ to $(Y,\mathcal {J})$ and let $A\in \mathcal {I}^{+}.$ We know that $A\subseteq f^{-1}\left ( f\left [ A\right ] \right ) ,$ hence $f^{-1}\left ( f\left [ A\right ] \right ) \in \mathcal {I}^{+}.$ Since f is a Katětov function, we must have that $f\left [ A\right ] \in \mathcal {J}^{+}.$

Now assume that f sends $\mathcal {I}^{+}$ sets to $\mathcal {J}^{+}$ sets, we will prove that f is a Katětov function. Let $B\in \mathcal {J}.$ Since $f[f^{-1}\left ( B\right ) ]\subseteq B,$ it follows that $f[f^{-1}\left ( B\right ) ]\in \mathcal {J}.$ Using the hypothesis we conclude that $f^{-1}\left ( B\right ) \in \mathcal {I}.$

We now recall some special properties of MAD families, which will play a crucial role in the paper.

Definition 12. Let $\mathcal {A}$ be a MAD family.

1. $\mathcal {A}$ is tight if for every $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \mathcal {I}\left ( \mathcal {A}\right ) ^{+}$ there is $B\in \mathcal {I}\left ( \mathcal {A}\right ) $ such that $B\cap X_{n}$ is infinite for every $n\in \omega .$
2. $\mathcal {A}$ is weakly tight if for every $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \mathcal {I}\left ( \mathcal {A}\right ) ^{+}$ there is $B\in \mathcal {I}\left ( \mathcal {A}\right ) $ such that $\left \vert B\cap X_{n}\right \vert =\omega $ for infinitely many $n\in \omega .$
3. $\mathcal {A}$ is completely separable if for every $X\in \mathcal {I(A)}^{+}$ there is $A\in \mathcal {A}$ such that $A\subseteq X.$

It is currently unknown if ZFC implies the existence of any of this type of MAD families, but significant progress has been obtained in each case. The existence of a completely separable MAD family is a famous problem of Erdoős and Shelah (see [Reference Erdős and Shelah20], also [Reference Hrušák, Steprans and Zhang43]). It is easy to prove that consistently the answer is affirmative. Most of the early work on this problem was done by Balcar and Simon (see [Reference Balcar and Simon2]). They proved that completely separable MAD families exist assuming one of the following: $\mathfrak {a=c}$ , $\mathfrak {b=d,} \mathfrak {d\leq a}$ , or $\mathfrak {s} =\omega _{1}.$ A major advance was done by Shelah himself in [Reference Shelah61] (see also [Reference Guzmán28, Reference Hrušák38, Reference Mildenberger, Raghavan and Steprans56]). He proved that there is a completely separable MAD family if either $\mathfrak {s<a}$ or $\mathfrak {s\geq a}$ and a certain “PCF hypothesis” holds. In [Reference Mildenberger, Raghavan and Steprans56] Mildenberger, Raghavan, and Steprāns (building from results in [Reference Raghavan and Steprāns59]) were able to eliminate the extra hypothesis in the case of $\mathfrak {s=a.}$ In this way, $\mathfrak {s\leq a}$ implies that there is a completely separable MAD family. Moreover, building from the work of Shelah, Mildenberger, Raghavan, and Steprāns proved the following theorem:

Theorem 13 (Mildenberger, Raghavan, and Steprāns [Reference Mildenberger, Raghavan and Steprans56] and [Reference Raghavan and Steprāns59]).

If $\mathfrak {s\leq b,}$ then there is a completely separable weakly tight MAD family.

Regarding tight MAD families, Hrušák and Kurilic independently proved the following:

Proposition 14 (Hrušák [Reference Hrušák36], Kurilic [Reference Kurilić51]).

$\mathfrak {b=c}$ implies that there is a completely separable tight MAD family.

In [Reference Guzmán and Hrušák32] it is proved that the diamond principle $\Diamond (\mathfrak {b})$ of [Reference Moore, Hrušák and Džamonja58] also implies that there is a tight MAD family.

Lemma 15. Let $\mathcal {A}$ and $\mathcal {B}$ be two MAD families. If $\mathcal {A}$ is (weakly) tight and $\mathcal {A}\leq _{\textsf {K}} \mathcal {B},$ then $\mathcal {B}$ is also (weakly) tight.

Proof Let $f\in \omega ^{\omega }$ be a Katětov function from $(\omega ,\mathcal {I(B)})$ to $(\omega ,\mathcal {I(A)}).$ Let $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \mathcal {I(B)}^{+}.$ By Lemma 11, we know that $\left \{ f\left [ X_{n}\right ] \mid n\in \omega \right \} \subseteq \mathcal {I(A)}^{+}.$ Since $\mathcal {A}$ is (weakly) tight, we can find $A\in \mathcal {I(A)}$ such that $A\cap f\left [ X_{n}\right ] $ is infinite for all (for infinitely many) $n\in \omega .$ It follows that $f^{-1}\left ( A\right ) \in \mathcal {I(B)}$ and has infinite intersection with all (infinitely many) of the $X_{n}.$

We now recall the notion of forcing destructibility:

Definition 16. Let $\mathbb {P}$ be a forcing notion, $\mathcal {I}$ an ideal and $\mathcal {A}$ a MAD family.

1. $\mathcal {I}$ is $\mathbb {P}$ -destructible if $\mathcal {I}$ is no longer tall after forcing with $\mathbb {P}.$
2. $\mathcal {A}$ is $\mathbb {P}$ -destructible if $\mathcal {A}$ is no longer maximal after forcing with $\mathbb {P}.$

It is easy to see that a MAD family is $\mathbb {P}$ -destructible if and only if its ideal generated is $\mathbb {P}$ -destructible. The topic of indestructibility has obtained a lot of attention recently, yet there are still many interesting problems that remain open. To learn more about indestructibility of ideals and MAD families, the reader may consult [Reference Brendle and Yatabe9, Reference Hrušák and Zapletal44] and the survey [Reference Chodounský and Guzmán14]. Forcing indestructibility and the Katětov order are related as follows:

Lemma 17 [Reference Hrušák and Ferreira40].

Let $\mathcal {I}$ and $\mathcal {J}$ be two ideals and $\mathbb {P}$ a forcing notion. If $\mathcal {I}\leq _{\textsf {K}}\mathcal {J}$ and $\mathbb {P}$ destroys $\mathcal {J},$ then $\mathbb {P}$ also destroys $\mathcal {I}.$

By $\mathbb {C}$ we will denote Cohen forcing. There is a nice characterization of Cohen indestructibility. By nwd we denote the ideal of all nowhere dense subsets of the rational numbers. We have the following:

Proposition 18 [Reference Brendle and Yatabe9, Reference Hrušák and Zapletal44].

Let $\mathcal {I}$ be an ideal. The following are equivalent $:$

1. $\mathcal {I}$ is $\mathbb {C}$ -destructible.
2. $\mathcal {I}\leq _{\textsf {K}}$ nwd.

More results of this type can be found in [Reference Brendle and Yatabe9, Reference Hrušák and Zapletal44]. It is easy to see that tight MAD families are $\mathbb {C} $ -indestructible. The converse does not hold (in fact, $\mathbb {C} $ -indestructibility does not even imply weak tightness). However, this two notions are very related:

Proposition 19 [Reference Hrušák and Ferreira40, Reference Kurilić51].

Let $\mathcal {A}$ be a MAD family. If $\mathcal {A}$ is Cohen indestructible, then there is $X\in \mathcal {I(A)}^{+}$ such that $\mathcal {A}\upharpoonright X$ is tight.

In particular, there is a $\mathbb {C}$ -indestructible MAD family if and only if there is a tight MAD family.

Definition 20. Let $X,Y$ be countable sets, $\mathcal {A}$ a MAD family in X and $\mathcal {B}$ a MAD family in $Y.$

1. Let $g:Y\longrightarrow X$ be a function. We say that g is a strong Katětov function from $(Y,\mathcal {B})$ to $(X,\mathcal {A})$ if g is a Katětov function from $(Y,\mathcal {B})$ to $(X,\mathcal {A})$ and for every $B\in \mathcal {I}\left ( B\right ) ,$ we have that $g\left [ B\right ] \in \mathcal {I}(\mathcal {A}).$
2. We say that $\mathcal {A} \leq _{\textsf {SK}}\mathcal {B}$ if there is a strong Katětov function from $(Y,\mathcal {B})$ to $(X,\mathcal {A}).$

In spite of the name, the order $\leq _{\textsf {SK}}$ is not that much different than $\leq _{\textsf {K}}$ when working with weakly tight MAD families, as will be explained in the lemma below. All the relevant ideas are already contained (at least implicitly) in [Reference Hrušák and Ferreira40].

Lemma 21. Let $\mathcal {A}$ and $\mathcal {B}$ be two MAD families on $\omega .$

1. If $X\in \mathcal {I(A)}^{\ast },$ then $\mathcal {A}\upharpoonright X$ and $\mathcal {A}$ are Katětov equivalent.
2. If f is a Katětov function from $(\omega ,\mathcal {B})$ to $(\omega ,\mathcal {A}),$ then the set $\{B\in \mathcal {B}\mid f\left [ B\right ] \in \left [ \omega \right ] ^{<\omega }\}$ is finite.
3. If $\mathcal {A}\leq _{\textsf {K}}\mathcal {B},$ then there is $X\in \mathcal {I(B)}^{\ast }$ and a Katětov function f from $(X,\mathcal {B}\upharpoonright X)$ to $(\omega ,\mathcal {A})$ such that if $B\in \mathcal {B}\upharpoonright X,$ then $f\left [ B\right ] $ is infinite (recall that $\mathcal {B}\upharpoonright X=_{\textsf {K}}\mathcal {B}$ by the first point).
4. If g is a Katětov function from $(\omega ,\mathcal {B})$ to $(\omega ,\mathcal {A})$ and $\mathcal {A}$ is weakly tight, then the set $\{B\in \mathcal {B}\mid f[B]\in \mathcal {I(A)}^{+}\}$ is finite.
5. If $\mathcal {A}\leq _{\textsf {K}}\mathcal {B}$ and $\mathcal {A}$ is weakly tight, then there is a MAD family $\mathcal {B}_{1}$ such that $\mathcal {B}=_{\textsf {K}}\mathcal {B}_{1}$ and $\mathcal {A} \leq _{\textsf {SK}}\mathcal {B}_{1}.$

Proof We start with the first point. Let $X\in \mathcal {I(A)}^{\ast },$ we only need to prove that $\mathcal {A}\upharpoonright X \leq _{\textsf {K}} \mathcal {A}$ (see Lemma 10). Choose n any point in $X.$ Define $f:\omega \longrightarrow X$ where $f\upharpoonright X$ is the identity and $f\upharpoonright (\omega \setminus X)$ is constant $n.$ This is a Katětov function from $(\omega ,\mathcal {A})$ to $(X,\mathcal {A} \upharpoonright X).$

For the second point, assume that there are distinct $B_{0},B_{1} ,\dots \in \mathcal {B}$ such that $f\left [ B_{n}\right ] $ is finite for every $n\in \omega .$ For each $n\in \omega ,$ choose $b_{n}\in f\left [ B_{n}\right ] $ such that $f^{-1}\left ( \left \{ b_{n}\right \} \right ) \cap B_{n}$ is infinite. Let $S=\left \{ b_{n}\mid n\in \omega \right \} .$ If S is finite, then $f^{-1}\left ( S\right ) \in \mathcal {I(B)}^{+},$ which is a contradiction. If S is infinite, find $A\in \mathcal {A}$ such that $A\cap S$ is infinite. It follows that $f^{-1}\left ( A\right ) \in \mathcal {I(B)}^{+},$ which is also a contradiction.

We now prove the third point. Let $\mathcal {A}\leq _ {\textsf {K}} \mathcal {B}$ and choose f a Katětov function from $(\omega ,\mathcal {B})$ to $(\omega ,\mathcal {A}).$ Let $D=\bigcup \{B\in \mathcal {B}\mid f\left [ B\right ] \in \left [ \omega \right ] ^{<\omega }\}$ which we know is in $\mathcal {I(B)}$ by the previous point. Define $X=\omega \setminus D$ and consider the restriction of f to $X.$

We now prove point 4. Assume that there are distinct $B_{0},B_{1} ,\dots \in \mathcal {B}$ such that $f\left [ B_{n}\right ] \in \mathcal {I(A)}^{+}$ for every $n\in \omega .$ Since $\mathcal {A}$ is weakly tight, there is $A\in \mathcal {I(A)}$ such that $A\cap f[B_{n}]$ is infinite for infinitely many $n\in \omega .$ It follows that $f^{-1}\left ( A\right ) \in \mathcal {I(B)} ^{+},$ which is a contradiction.

The last point follows with the same argument as the one of point 3, but using point 4 instead of point 2.

We now review the notion of trace ideal. Define the mapping $\pi :\mathcal {P}\left ( 2^{<\omega }\right ) \longrightarrow \mathcal {P}\left ( 2^{\omega }\right ) $ as $\pi \left ( a\right ) =\{x\in 2^{\omega }\mid \exists ^{\infty }s\in a\left ( s\subseteq x\right ) \}.$ It is not hard to see that $\pi \left ( a\right ) $ is always a $G_{\delta }$ -set. If $\mathcal {K}$ is a $\sigma $ -ideal on $2^{\omega },$ its trace ideal is defined as tr( $\mathcal {K}$ ) $=\{a\subseteq 2^{\omega }\mid \pi \left ( a\right ) \in \mathcal {K}\}.$ Trace ideals are fundamental in the study of forcing indestructibility. It is interesting that the indestructibility of the most important forcing notions can be characterized using the Katětov order and trace ideals. The reader may consult [Reference Brendle and Yatabe9, Reference Hrušák and Zapletal44] to learn about this. The trace ideals will not be needed until Section 6 and in there we will review the results needed for this paper.

4 Katětov-top MAD families vs. $\mathfrak {s\leq b}$

We say a MAD family $\mathcal {A}$ is Katětov-top if $\mathcal {A}$ is Katětov above every other MAD family. This notion was first consider by García-Ferreira and Hrušák in [Reference Hrušák and Ferreira40], where they proved that such families do not exist assuming $\mathfrak {b=c}.$ The purpose of this section is to improve this result.

A Katětov-top MAD family would have really strong combinatorial properties:

Lemma 22. Let $\mathcal {A}$ be a Katětov-top MAD family and $\mathbb {P}$ a partial order.

1. The size of $\mathcal {A}$ is $\mathfrak {a}.$
2. If there is a weakly tight MAD family, then $\mathcal {A}$ is weakly tight.
3. If there is a tight MAD family, then $\mathcal {A}$ is tight.
4. If $\mathbb {P}$ destroys $\mathcal {A},$ then $\mathbb {P}$ destroys every other MAD family.
5. If there is a $\mathbb {P}$ -indestructible MAD family, then $\mathcal {A}$ is $\mathbb {P}$ -indestructible.

Proof This are trivial consequences of Lemmata 10, 15, and 17.

It is the common belief that Katětov-top MAD families should not exist, yet we only have partial answers. In this section, we will prove that the cardinal invariant inequality $\mathfrak {s\leq b}$ implies that there are no Katětov-top MAD families. In fact, we will prove even more. Informally speaking, we will prove that if we “know how to construct a weakly tight completely separable MAD family,” then we can show that there are no Katětov-top MAD families. In order to formalize this statement, we need the following definition:

Definition 23. Let $\mathbb {P}$ be a partial order. We say that $\mathbb {P}$ is a forcing notion for a weakly tight family if the following conditions hold $:$

1. If $p\in \mathbb {P},$ then p is of the form $p=(\mathcal {A}_{p},R_{p})$ where $\mathcal {A}_{p}$ is an AD family with $\left \vert \mathcal {A}_{p}\right \vert <\mathfrak {c}$ and $R_{p}\in $ H $\left ( \mathfrak {c}^{+}\right ) .$ Footnote ³
2. If $p\leq q,$ then $\mathcal {A}_{q}\subseteq \mathcal {A}_{p}.$
3. ( $\mathfrak {c}$ -closed) Let $\kappa <\mathfrak {c}.$ If $\left \{ p_{\alpha }\mid \alpha <\kappa \right \} \subseteq \mathbb {P}$ is a decreasing sequence and $\mathcal {B}=\bigcup \limits _{\alpha <\kappa }\mathcal {A} _{p_{\alpha }}$ has size less than $\mathfrak {c},$ then there is a condition $q=(\mathcal {B},R)\in \mathbb {P}$ such that $q\leq p_{\alpha }$ for every $\alpha <\kappa .$
4. For every $p\in \mathbb {P}$ and $X\in \mathcal {I(A}_{p}\mathcal {)}^{+},$ there is $q\in \mathbb {P}$ with the following properties $:$
1. (a) $q\leq p.$
2. (b) $\left \vert \mathcal {A}_{q}\right \vert \leq \left \vert \mathcal {A} _{p}\right \vert +\omega .$
3. (c) There are $A_{0}, A_{1},\dots \in \mathcal {A}_{q}\setminus \mathcal {A}_{p}$ pairwise distinct such that $A_{n}\subseteq X$ for every $n\in \omega .$
5. For every $p\in \mathbb {P}$ and $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \mathcal {I(A}_{p}\mathcal {)}^{+},$ there is $q\in \mathbb {P}$ such that $:$
1. (a) $q\leq p.$
2. (b) $\left \vert \mathcal {A}_{q}\right \vert \leq \left \vert \mathcal {A} _{p}\right \vert +\omega .$
3. (c) There is $A\in \mathcal {I(A}_{q}\mathcal {)}$ such that there are infinitely many $n\in \omega $ for which $\left \vert X_{n}\cap A\right \vert =\omega .$

Let $p=(\mathcal {A}_{p},R_{p})$ be an element of $\mathbb {P}.$ The purpose of $R_{p}$ is simply to be a parameter, probably needed to define $\leq $ (or to be used in a recursive construction). It is worth pointing out that while $p\leq q$ implies $\mathcal {A}_{q}\subseteq \mathcal {A}_{p},$ in general the converse does not need to hold. Note that by Point 4 above, $\mathcal {A}_{p}$ is a nowhere MAD family.

Intuitively, the definition tries to formalize the idea that we “know a method to recursively construct a completely separable weakly tight MAD family.” It is trivial to build a completely separable weakly tight MAD family assuming the existence of a forcing notion for a weakly tight family. It is easy to see that the proofs of Proposition 14 (see [Reference Hrušák36, Reference Kurilić51]) in fact show that $\mathfrak {b=c}$ imply that there is a forcing notion for a weakly tight family (in fact, in this case we can take $\mathbb {P}$ to be the set of all AD families of size less than $\mathfrak {c},$ ordered by reverse inclusion. There is no need of the parameters mentioned in the first point of Definition 23). The proof of Theorem 13 actually shows that $\mathfrak {s\leq b}$ implies that there is a forcing notion for a weakly tight family (this time, the description of the forcing is more elaborated than in the case of $\mathfrak {b=c},$ but the reader familiar with [Reference Raghavan and Steprāns59] will have no problem extracting the forcing notion from the proof of the main theorem of the paper). It is currently unknown if ZFC proves that there is a forcing notion for a weakly tight family. The reader may consult [Reference Corral and Hrušák16] for another application of $\mathfrak {s\leq b}$ to MAD families.

We will now prove that there is no Katětov-top MAD family if there is a forcing notion for a weakly tight family. We start with the following lemma:

Lemma 24. Let $\mathbb {P}$ be a forcing notion for a weakly tight family, $\mathcal {B}$ a MAD family, $p=(\mathcal {A}_{p},R_{p})\in \mathbb {P}$ and $h\in \omega ^{\omega }$ an injective function. There is $q\in \mathbb {P}$ with the following properties $:$

1. $q\leq p.$
2. $\left \vert \mathcal {A}_{q}\right \vert \leq \left \vert \mathcal {A} _{p}\right \vert +\omega .$
3. If $\mathcal {D}$ is any MAD family with $\mathcal {A} _{q}\subseteq \mathcal {D},$ then h is not a strong Katětov function from $(\omega ,\mathcal {B})$ to $(\omega ,\mathcal {D}).$

Proof If h is not a Katětov function from $(\omega ,\mathcal {B})$ to $(\omega ,\mathcal {A}_{p}),$ there is nothing to do, so we assume it is. We know that $h\left [ \omega \right ] \in \mathcal {I(A}_{p}\mathcal {)}^{+}$ and since $\mathcal {A}_{p}$ is nowhere MAD, there is an infinite $Y\subseteq h\left [ \omega \right ] $ with $Y\in \mathcal {A}_{p}^{\perp }.$ Since h is injective, it follows that $h^{-1}\left ( Y\right ) $ is infinite. Since $\mathcal {B}$ is maximal, we can find and infinite $W\in \mathcal {I(B)}$ contained in $h^{-1}\left ( Y\right ) .$

By Point 4 of Definition 23, we can find $q\leq p$ such that $\left \vert \mathcal {A}_{q}\right \vert \leq \left \vert \mathcal {A}_{p}\right \vert +\omega $ and $h\left [ W\right ] $ contains infinitely many elements of $\mathcal {A} _{q}.$ In this way, $h\left [ W\right ] \in \mathcal {I}\left ( \mathcal {A} _{q}\right ) ^{++}.$ It follows that if $\mathcal {D}$ is any MAD family extending $\mathcal {A}_{q},$ then $h\left [ W\right ] \in \mathcal {I}\left ( \mathcal {D}\right ) ^{+}$ , so h is not a strong Katětov function from $(\omega ,\mathcal {B})$ to $(\omega ,\mathcal {D}).$

The following is a well-known and very useful theorem of Mathias:

Theorem 25 (Mathias [Reference Mathias54]).

Let $\mathcal {A}$ be a MAD family and $f\in \omega ^{\omega }.$ There is $X\in \mathcal {I}^{+}(\mathcal {A})$ such that either $f\upharpoonright X$ is constant or $f\upharpoonright X$ is injective.

The proof of the following lemma is nearly identical to the one of Proposition 3.7 of [Reference Hrušák and Ferreira40]:

Lemma 26. Let $\mathcal {A}$ and $\mathcal {B}$ be MAD families with $\mathcal {A}$ weakly tight. If $\mathcal {A}\leq _{\textsf {K}} \mathcal {B},$ then there are X and h with the following properties $:$

1. $X\in \mathcal {I(B)}^{+}.$
2. $h:X\longrightarrow \omega $ is injective and a strong Katětov function from $(X,\mathcal {B}\upharpoonright X)$ to $(\omega ,\mathcal {A} ).$

Proof Let $f\in \omega ^{\omega }$ be a Katětov function from $(\omega ,\mathcal {B})$ to $(\omega ,\mathcal {A}).$ By the theorem of Mathias above, we can find $X_{0}\in \mathcal {I(B)}^{+}$ such that either $f\upharpoonright X_{0}$ is constant or $f\upharpoonright X_{0}$ is injective. However, the former case can not occur, since $X_{0}\in \mathcal {I(B)}^{+}$ and f is a Katětov function. Note that $f\upharpoonright X_{0}$ is an injective Katětov function form $(X_{0},X_{0}\upharpoonright \mathcal {B})$ to $(\omega ,\mathcal {A}).$

Let $L=\{B\in \mathcal {B}\mid f\left [ B\right ] \in \mathcal {I(A)}^{+}\}.$ Since $\mathcal {A}$ is weakly tight, by Point 4 of Lemma 21, we know that L is a finite set. Let $X=X_{0} \setminus \bigcup L$ and $h=f\upharpoonright X.$ It is clear that X and h have the desired properties.

We can now prove the main theorem of the section:

Theorem 27. If there is a forcing notion for a weakly tight family, then there are no Katětov-top MAD families.

Proof Fix $\mathbb {P}$ a forcing notion for a weakly tight family and $\mathcal {B}$ a MAD family. Using $\mathbb {P},$ we will find a MAD family that is not Katětov below $\mathcal {B}.$ With the aid of Lemma 24 and a careful bookkeeping device, we can build a MAD family $\mathcal {A}$ with the following properties:

1. $\mathcal {A}$ is completely separable and weakly tight.
2. For every $X\in \mathcal {I(B)}^{+}$ and an injective $h:X\longrightarrow \omega ,$ we have that h is not a strong Katětov function from $(X,\mathcal {B}\upharpoonright X)$ to $(\omega ,\mathcal {A}).$

In this way, $\mathcal {A}$ is a weakly tight MAD family such that for every $X\in \mathcal {I(B)}^{+},$ there is no injective strong Katětov function from $(X,\mathcal {B}\upharpoonright X)$ to $(\omega ,\mathcal {A}).$ By Lemma 26, it follows $\mathcal {A}$ is not Katětov below $\mathcal {B}.$

As mentioned before, by Theorem 13 and a comment above, we get the following:

Corollary 28. If $\mathfrak {s\leq b},$ then there are no Katětov-top MAD families.

Recall from the introduction that García-Ferreira and Hrušák proved a similar theorem assuming $\mathfrak {b=c}$ (see [Reference Hrušák and Ferreira40]), so our result generalizes theirs. It is worth mentioning that Raghavan has extended the work in [Reference Raghavan and Steprāns59] and obtain weakly tight MAD families in models of $\mathfrak {b<s}.$ In fact, he proved under $\mathfrak {b<s,}$ that if certain “PCF hypothesis” are true, then weakly tight MAD families exist. It is very likely that his arguments actually show that there is a forcing notion for a weakly tight family under those assumptions. Unfortunately, the theorems of Raghavan remain unpublished. It is our hope that someday, the need for the extra hypothesis in the case $\mathfrak {b<s}$ will be eliminated, providing both a ZFCconstruction of a weakly tight completely separable MAD family and a proof that there are no Katětov-top MAD families.

5 A Katětov maximal MAD family from $\mathfrak {b=c}$

A MAD family $\mathcal {A}$ is Katětov maximal if there is no MAD family that is strictly above $\mathcal {A}$ in the Katětov order. Obviously, a Katětov-top MAD family would be Katětov maximal. However, unlike the case of Katětov-top MAD families, we know that Katětov maximal MAD families may consistently exist. This was first proved by Arciga, Hrušák, and Martínez in [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1]. In fact, they proved that $\mathfrak {t=c}$ implies that there is a Katětov maximal MAD family. We will now improve this result. Our method is a refinement of theirs. Although in the paper they assumed $\mathfrak {t=c},$ it is not hard to see that their arguments can be carried out under $\mathfrak {h=c}$ . The Katětov maximal MAD family is constructed recursively. At any given step of the recursion, there are less than $\mathfrak {c}$ many open dense subsets of $\left [ \omega \right ] ^{\omega }$ that need to be intersected in order to proceed. This is the reason that $\mathfrak {h=c}$ is enough to carry out the construction. It turns out that by being even more careful, it is possible to prove that $\mathfrak {b=c}$ is enough to intersect all the open dense sets that are needed in the recursion.

If we want to recursively construct a Katětov maximal MAD family, we immediately run into a conceptual problem. A MAD family needs to be constructed in (at most) $\mathfrak {c}$ steps, while there are $2^{\mathfrak {c}}$ MAD families to take care of. There are much more requirements than steps of the recursion. García-Ferreira and Hrušák found a very clever to way to circumvent the problem. First we need the following notion:

Definition 29. Let $\mathcal {A}$ be a MAD family. We say that $\mathcal {A}$ is Katětov uniform if $\mathcal {A}$ is Katětov equivalent to all of its restrictions.

Equivalently, $\mathcal {A}$ is Katětov uniform if and only if $\mathcal {A}\upharpoonright X\leq _{\textsf {K}}\mathcal {A}$ for every ${X\in \mathcal {I(A)}^{+}.}$ Every Katětov maximal MAD family is Katětov uniform. In [Reference Hrušák and Ferreira40] it was proved the following:

Proposition 30 [Reference Hrušák and Ferreira40].

Let $\mathcal {A}$ be a MAD family. If $\mathcal {A}$ is Katětov uniform and weakly tight, then $\mathcal {A}$ is Katětov maximal.

The great advantage of the Proposition is that in principle, constructing a weakly tight, Katětov uniform MAD family requires only $\mathfrak {c}$ many steps. In this way, if we want to build a Katětov maximal MAD family, it is enough to build a weakly tight, Katětov uniform MAD family. Thus we reduce the number of tasks needed from $2^{\mathfrak {c}}$ to $\mathfrak {c}.$ The drawback is that the MAD families constructed in this way are necessarily also weakly tight. It is currently unknown if Katětov maximality implies weak tightness (however, in the next section we show that it does not imply tightness).

In [Reference Hrušák and Ferreira40] a Katětov uniform MAD family was constructed assuming $\mathfrak {t=c}$ . The method used in there was not sufficient to build a maximal one. This was achieved until [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1] where a novel idea was employed: along the construction of the Katětov maximal MAD family, a partial cofinitary semigroup was also constructed. Partial cofinitary semigroups are related to the more well studied cofinitary groups. Maximal cofinitary groups have been deeply studied in Set Theory. The reader wishing to know more about this topic, may consult [Reference Brendle, Spinas and Zhang10, Reference Fischer, Schrittesser and Törnquist23, Reference Fischer and Törnquist22, Reference Gao and Zhang26, Reference Hrušák, Steprans and Zhang45, Reference Kastermans47, Reference Kastermans48].

We will denote by $Id$ the identity function on $\omega .$ We will now clarify what we mean by the composition of two partial functions from $\omega $ to $\omega .$

Definition 31. Let $f:A\longrightarrow \omega $ and $g:B\longrightarrow \omega $ where $A,B\subseteq \omega .$ The composition $gf:C\longrightarrow \omega $ is defined as follows $:$

1. $C=\left \{ a\in A\mid f\left ( a\right ) \in B\right \} .$
2. Let $a\in C.$ Define $gf\left ( a\right ) =x$ if $g\left ( f\left ( a\right ) \right ) =x.$

In other words, $gf=\left \{ \left ( a,x\right ) \mid a\in A\wedge \exists b\in B\left ( \left ( a,b\right ) \in f\wedge \left ( b,x\right ) \in g\right ) \right \} $ (see [Reference Enderton19]). If $f\in \omega ^{\omega }$ is an injective function, by $f^{-1}$ we denote the function with domain img $\left ( f\right ) $ and such that $f^{-1}f\left ( n\right ) =n$ for every $n\in \omega .$ The following lemma is a particular case of Theorem 3G of [Reference Enderton19].

Lemma 32. Let $f:\omega \longrightarrow \omega $ be an injective function and $A\subseteq \omega .$

1. $f^{-1}f$ is the identity function on $\omega .$
2. $\,ff^{-1}$ is the identity function on img $\left ( f\right ) .$
3. $f^{-1}f\left [ A\right ] =A$ and $ff^{-1}\left [ A\right ] \subseteq A$ (but might be smaller).

It is worth emphasizing that in general, the functions we will be using will be injections but not surjections on $\omega .$ We need to be very careful when canceling. The reason we explicitly wrote the previous lemma is to remind the reader which cancellations are valid and which ones are not.

Definition 33. Let $S\subseteq \omega ^{\omega }$ be a family of injective functions. We say that a partial function $w;\omega \longrightarrow \omega $ is a (reduced) word on S if there are $f_{1},\dots ,f_{n}\in S$ and $r_{1},\dots ,r_{n} \in \mathbb {Z}$ such that $:$

1. $r_{i}\neq 0$ for all $i\leq n.$
2. $w=f_{1}^{r_{1}}f_{2}^{r_{2}}\dots f_{n}^{r_{n}}.$
3. $f_{i+1}\notin \left \{ f_{i},f_{i}^{-1}\right \} $ and $f_{i} \notin \left \{ f_{i+1},f_{i+1}^{-1}\right \} $ for all $i<n.$

We would like to point out that for us, a word is an actual partial function. Not a symbolic representation of it. It is easy to see that if w is a word, then $w^{-1}$ is also a word. Note that if $f\in S,$ then dom $\left ( f\right ) =\omega ,$ but the domain of $f^{-1}$ might be a proper subset of $\omega .$

By $\mathbb {W}\left ( S\right ) $ we denote the set of all reduced words on $S.$ It is clear that if $w\in \mathbb {W}\left ( S\right ) ,$ then w is an injective partial function and $w^{-1}$ is also in $\mathbb {W}\left ( S\right ) .$ It is easy to see that $\left \vert \mathbb {W}\left ( S\right ) \right \vert \leq \left \vert S\right \vert +\omega .$ Given $w\in \mathbb {W}\left ( S\right ) $ , $f_{1},\dots ,f_{n}\in S$ and $r_{1},\dots ,r_{n}\in \mathbb {Z}$ as above, we will implicitly assume that if $n\neq 1,$ then each $f_{i}\neq Id,$ and ff $n=1$ and $f_{1}=Id,$ then $r_{1}=1.$ Every word has a length, which is computed in the following way: let $w\in \mathbb {W}\left ( S\right ) ,$ the length of w is smallest number of the form $\underset {i\leq n}{\sum }|r_{i}|$ where $w=f_{1}^{r_{1}}f_{2}^{r_{2}}\dots f_{n}^{r_{n}}$ are as above.

Lemma 34. Let $S\subseteq \omega ^{\omega }$ be a family of injective functions and $p,q,w\in \mathbb {W}\left ( S\right ) .$ If $A\subseteq \omega ,$ then $pww^{-1}q\left [ A\right ] \subseteq pq\left [ A\right ] .$

We now introduce the following notion, which will play a key role in the rest of the paper:

Definition 35. Let $S\subseteq \omega ^{\omega }.$ We say that S is a partial cofinitary semigroup base if the following conditions hold $:$

1. S is a family of injective functions.
2. $Id\in S.$
3. $\mathbb {W}\left ( S\right ) $ is an AD family (we view every partial function as a subset of $\omega \times \omega $ ).

We would like to point out that $\mathbb {W}\left ( S\right ) $ may not be a semigroup. This is because while $\mathbb {W}\left ( S\right ) $ is closed under many compositions, it may not closed under all of them (for example, if $f\in S,$ then $ff^{-1}$ may not be in $\mathbb {W}\left ( S\right ) $ ).

Given a partial function $f,$ define Fix $\left ( f\right ) =\{n\in $ dom $\left ( f\right ) \mid f\left ( n\right ) =n\}.$ We now have the following:

Lemma 36. Let S be a partial cofinitary semigroup base and $w\in \mathbb {W}\left ( S\right ) .$ If $w\neq Id,$ then Fix $\left ( w\right ) $ is finite.

Proof The lemma follows because $Id\in S,$ so w and $Id$ are almost disjoint.

An important feature of partial cofinitary semigroup bases is the following:

Lemma 37. Let S be a partial cofinitary semigroup base, $w,z\in \mathbb {W}\left ( S\right ) $ with $w\neq z$ and $X\in \left [ \omega \right ] ^{\omega }.$ There is $Y\in \left [ X\right ] ^{\omega }$ such that $w\left [ Y\right ] \cap z\left [ Y\right ] =\emptyset .$

Proof We will recursively define $Y=\left \{ y_{n}\mid n\in \omega \right \} \subseteq X$ as follows: First, we choose $y_{0}\in X$ such that either $y_{0}\notin $ dom $\left ( w\right ) \cap $ dom $\left ( z\right ) $ or $w\left ( y_{0}\right ) \neq z\left ( y_{0}\right ) $ (recall that w and z are almost disjoint). Assume we have defined $y_{0},\dots ,y_{n},$ we will now define $y_{n+1}.$ Let $t_{n+1}=\left \{ y_{0},\dots ,y_{n}\right \} .$ We now choose $y_{n+1}\in X$ with the following properties:

1. $y_{n+1}\notin t_{n+1}\cup z^{-1}\left ( w\left [ t_{n+1}\right ] \right ) \cup w^{-1}\left ( z\left [ t_{n+1}\right ] \right ) .$
2. Either $y_{n+1}\notin $ dom $\left ( w\right ) \cap $ dom $\left ( z\right ) $ or $\ w\left ( y_{n+1}\right ) \neq z\left ( y_{n+1}\right ) .$

This is easy to do since both w and z are injective and they are almost disjoint. We claim that $Y=\left \{ y_{n}\mid n\in \omega \right \} $ is as desired. Assume this is not the case, so there are $i,j\in \omega $ such that $w\left ( y_{i}\right ) =z\left ( y_{j}\right ) .$ By construction, it is impossible that $i=j.$ Assume that $i<j$ (the other case is symmetrical). We get that $y_{j}\in z^{-1}\left ( w\left [ t_{j}\right ] \right ) ,$ but this is impossible.

We will now recall the following definitions:

Definition 38.

1. Let $h:\omega ^{<\omega \nearrow }\longrightarrow \omega .$ A function $\pi :\omega ^{<\omega \nearrow }\longrightarrow \left [ \omega \right ] ^{<\omega }$ is an h-slalom predictor if $\left \vert \pi \left ( s\right ) \right \vert \leq h\left ( s\right ) $ for every $s\in \omega ^{<\omega \nearrow }.$
2. Let $\pi :\omega ^{<\omega \nearrow }\longrightarrow \left [ \omega \right ] ^{<\omega }$ and $g\in \omega ^{\omega }$ an increasing function. We say that g escapes from $\pi $ if there are only finitely many $n\in \omega $ for which $g\left ( n\right ) \in \pi (g\upharpoonright n)$ .

In [Reference Brendle and Yatabe10], Brendle, Spinas, and Zhang proved the following very useful theorem:

Theorem 39 [Reference Brendle and Yatabe10].

Let $\kappa $ be an infinite cardinal. The following are equivalent $:$

1. $\kappa <$ non $\left ( \mathcal {M}\right ) .$
2. For every $h:\omega ^{<\omega \nearrow }\longrightarrow \omega $ and $\left \{ \pi _{\alpha }\mid \alpha <\kappa \right \} $ a set of h-slalom predictors, there is $g\in \omega ^{\omega }$ an increasing function that escapes from each of the $\pi _{\alpha }.$

With this theorem, we can prove the following:

Proposition 40. Let S be a partial cofinitary semigroup base with $\left \vert S\right \vert <$ non $\left ( \mathcal {M}\right ) $ and $X\in \left [ \omega \right ] ^{\omega }.$ There is $Y\in \left [ X\right ] ^{\omega }$ such that for all $w,z\in \mathbb {W}\left ( S\right ) ,$ if $w\neq z,$ then $w\left [ Y\right ] \cap z\left [ Y\right ] $ is finite.Footnote ⁴

Proof Let $l:\omega \longrightarrow X$ be its enumerating function and $\mathbb {W} \left ( S\right ) =\left \{ w_{\alpha }\mid \alpha <\kappa \right \} $ (for some cardinal $\kappa $ that is smaller than non $\left ( \mathcal {M} \right ) $ ). Given $\alpha ,\beta <\kappa $ with $\alpha \neq \beta ,$ we define the slalom predictor:

$\begin {array} [c]{c} \pi _{\alpha \beta }:\omega ^{<\omega \nearrow }\longrightarrow \left [ \omega \right ] ^{<\omega }. \end {array} $

Given as follows:

1. $\pi _{\alpha \beta }\left ( \emptyset \right ) =\emptyset .$
2. Let $t\in \omega ^{<\omega \nearrow }$ with $t\neq \emptyset .$ Define:

$\begin {array} [c]{cccc} \pi _{\alpha \beta }\left ( t\right ) & = & \textsf {img}\left ( t\right ) & \cup \\ & & l^{-1}(w_{\alpha }^{-1}(w_{\beta }[l[{\textsf {img}}\left ( t\right ) ]])) & \cup \\ & & l^{-1}(w_{\beta }^{-1}(w_{\alpha }[l[{\textsf {img}}\left ( t\right ) ]])). & \end {array} $

It is easy to see that there is a function $h:\omega ^{<\omega \nearrow }\longrightarrow \omega $ such that each $\pi _{\alpha \beta }$ is an h-slalom predictor. Since $\kappa $ is smaller than non $\left ( \mathcal {M} \right ) ,$ by Theorem 39, we know there is an increasing function $g\in \omega ^{\omega }$ that escapes from each $\pi _{\alpha \beta }.$ Define $Y=\left \{ l\left ( g\left ( n\right ) \right ) \mid n\in \omega \right \} .$ Since g is injective, it follows that Y is an infinite subset of $X.$ We will show that Y has the desired property. Let $\alpha ,\beta <\kappa $ with $\alpha \neq \beta ,$ we need to prove that $w_{\alpha }\left [ Y\right ] \cap w_{\beta }\left [ Y\right ] $ is finite. In order to achieve this, it is enough to prove that the set $P=\left \{ \left ( i,j\right ) \mid w_{\alpha }\left ( lg\left ( i\right ) \right ) =w_{\beta }\left ( lg\left ( j\right ) \right ) \right \} $ is finite. Let $\left ( i,j\right ) \in P.$

First, consider the case where $i\neq j.$ Without lost of generality, we may assume that $i<j.$ Let $t=g\upharpoonright j$ (so img $\left ( t\right ) =g\left [ j\right ] $ ). Clearly $w_{\alpha }\left ( lg\left ( i\right ) \right ) \in w_{\alpha }\left [ lg\left [ j\right ] \right ] ,$ so $w_{\beta }\left ( lg\left ( j\right ) \right ) \in w_{\alpha }\left [ lg\left [ j\right ] \right ] .$ In this way, $lg\left ( j\right ) \in w_{\beta } ^{-1}\left ( w_{\alpha }\left [ lg\left [ j\right ] \right ] \right ) $ and then, $g\left ( j\right ) \in l^{-1}\left ( w_{\beta }^{-1}\left ( w_{\alpha }\left [ lg\left [ j\right ] \right ] \right ) \right ) \subseteq \pi _{\alpha \beta }\left ( g\upharpoonright j\right ) .$ Since g escapes from $\pi _{\alpha \beta },$ there can only be finitely many $\left ( i,j\right ) $ in which this case holds.

In case $i=j,$ we would have that $w_{\alpha }\left ( lg\left ( i\right ) \right ) =w_{\beta }\left ( lg\left ( i\right ) \right ) .$ Since $w_{\alpha }$ and $w_{\beta }$ are almost disjoint, there are only finitely many pairs $\left ( i,j\right ) $ that fall in this case. This finishes the proof.

Recall that if S is a partial cofinitary semigroup base, then the identity mapping is in $S.$ In this way, under the hypothesis of the proposition above, if $w\in \mathbb {W}\left ( S\right ) $ and is not the identity, then $w\left [ Y\right ] \cap Y$ is finite. This fact will be used several times implicitly.

Definition 41. Let $S\subseteq \omega ^{\omega }$ be a partial cofinitary semigroup base and $\mathcal {A}$ an AD family. We say that S respects $\mathcal {A}$ if for every $w\in \mathbb {W}\left ( S\right ) $ and $A\in \mathcal {A},$ we have that $w\left [ A\right ] \in \mathcal {A}\cup \left [ \omega \right ] ^{<\omega }.$

We get the following:

Lemma 42. Let $S\subseteq \omega ^{\omega }$ be a partial cofinitary semigroup base and $\mathcal {A}$ an AD family such that S respects $\mathcal {A}.$ If $X\in \mathcal {A}^{\perp }$ and $w\in \mathbb {W}\left ( S\right ) ,$ then $w\left [ X\right ] \in \mathcal {A}^{\perp }.$

Proof We argue by contradiction. Assume that there is $A\in \mathcal {A}$ such that ${A\cap w\left [ X\right ] }$ is infinite. This implies that $w^{-1}\left ( A\right ) \cap X$ is infinite, but this is a contradiction since $w^{-1}\left ( A\right ) \in \mathcal {A}\cup \left [ \omega \right ] ^{<\omega }.$

We will use the following theorem of [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1], which is a generalization of a theorem in [Reference Brendle and Yatabe10]:

Proposition 43 [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1].

Let S be a partial cofinitary semigroup base with $\left \vert S\right \vert <$ non $\left ( \mathcal {M}\right ) .$ For every $Y\in \left [ \omega \right ] ^{\omega },$ there is an injective function $f:\omega \longrightarrow Y$ such that $S\cup \left \{ f\right \} $ is a partial cofinitary semigroup base.

We now introduce the following notion:

Definition 44. We say that $(S,\mathcal {A})$ is a nice pair if the following conditions hold $:$

1. S is a partial cofinitary semigroup base.
2. $\mathcal {A}\neq \emptyset $ is an AD family.
3. $\mathcal {L(}S,\mathcal {A)}=\{w\left [ A\right ] \mid w\in \mathbb {W}\left ( S\right ) \wedge A\in \mathcal {A}\}\setminus \lbrack \omega ]^{<\omega }$ is an AD family.

Note that if $(S,\mathcal {A})$ is a nice pair, it might not be the case that S respects $\mathcal {L(}S,\mathcal {A)}.$ For example, take $A\in \mathcal {A}$ and $f\in S.$ Clearly $f^{-1}\left [ A\right ] \in \mathcal {L(}S,\mathcal {A)},$ but $ff^{-1}\left [ A\right ] $ might be a proper subset of $A.$ Nevertheless, we can get a similar conclusion to the one of Lemma 42:

Lemma 45. Let $(S,\mathcal {A})$ be a nice pair and $Y\in \mathcal {L(}S,\mathcal {A)} ^{\perp }.$ If $w\in \mathbb {W}\left ( S\right ) ,$ then $w\left [ Y\right ] \in \mathcal {L(}S,\mathcal {A)}^{\perp }.$

Proof We will first prove that $w\left [ Y\right ] \in \mathcal {A}^{\perp }.$ If this was not the case, then there is $A\in \mathcal {A}$ such that $A\cap w\left [ Y\right ] $ is infinite. But this implies that $w^{-1}\left [ A\right ] \cap Y$ is infinite, which is a contradiction.

We now prove the general case. Once again, we proceed by contradiction. Assume this is not the case, so there is $z\in \mathbb {W}\left ( S\right ) $ and $A\in \mathcal {A}$ such that $z\left [ A\right ] \cap w\left [ Y\right ] $ is infinite. Note that it must be the case that $z\neq w,$ since $A\cap Y$ is finite and w is injective. Let $p,z_{1},w_{1}\in \mathbb {W}\left ( S\right ) $ such that:

1. $z=pz_{1}.$
2. $w=pw_{1}.$
3. $w_{1}^{-1}z_{1}$ is a reduced word.

By Lemma 34 we know that $w^{-1}z\left [ A\right ] \subseteq w_{1}^{-1}z_{1}\left [ A\right ] .$ Since $Y\in \mathcal {L(} S,\mathcal {A)}^{\perp },$ we know that $w_{1}^{-1}z_{1}\left [ A\right ] \cap Y$ is finite. But since $z\left [ A\right ] \cap w\left [ Y\right ] $ is infinite, this implies that $w^{-1}z\left [ A\right ] \cap Y$ is infinite, which is a contradiction.

We now prove the following:

Proposition 46. Let $(S,\mathcal {A})$ be a nice pair, $\left \vert S\right \vert <$ non $\left ( \mathcal {M}\right ) $ and $X\in \mathcal {L(} S,\mathcal {A)}^{\perp }.$ There is an injective function $h:\omega \longrightarrow X$ such that $(S\cup \left \{ h\right \} ,\mathcal {A})$ is a nice pair.

Proof Since the size of S is less than non $\left ( \mathcal {M}\right ) ,$ we can use Proposition 40 and find $Y\in \left [ X\right ] ^{\omega }$ such that for every $w,z\in \mathbb {W}(S)$ distinct, we have that $w\left [ Y\right ] \cap z\left [ Y\right ] $ is finite (recall that, in particular, if $z\neq Id,$ then $z\left [ Y\right ] \cap Y$ is finite). We now apply Proposition 43 and get an injective function $h:\omega \longrightarrow Y$ such that $S\cup \left \{ h\right \} $ is a partial cofinitary semigroup base. We will show that $(S\cup \left \{ h\right \} ,\mathcal {A})$ is a nice pair. We need some preliminary claims that will help us in order to achieve this.

Claim 47. Let $w\in \mathbb {W}\left ( S\cup \left \{ h\right \} \right ) .$ If w contains a subword of the form $h^{-1}zh$ with $z\in \mathbb {W}\left ( S\right ) $ (and $z\neq Id$ ), then img $\left ( w\right ) $ is finite.

It is enough to prove that the domain of $h^{-1}zh$ is finite. Recall that img $\left ( h\right ) \subseteq Y$ and $z\left [ Y\right ] \cap Y$ is finite. Since dom $\left ( h^{-1}\right ) =Y,$ it follows that the domain of $h^{-1}zh$ is finite.

Claim 48. If $w\in \mathbb {W}\left ( S\right ) $ and $A\in \mathcal {A},$ then $h^{-1}w\left [ A\right ] $ is finite.

Since $Y\in \mathcal {L(}S,\mathcal {A)}^{\perp },$ it follows that $Y\cap w\left [ A\right ] $ is finite. The domain of $h^{-1}$ is $Y,$ so the claim follows.

Note that the elements of $\mathbb {W}\left ( S\cup \left \{ h\right \} \right ) \setminus \mathbb {W}\left ( S\right ) $ are exactly the words in which h or $h^{-1}$ appear. We now prove the following:

Claim 49. If $w\in \mathbb {W}\left ( S\cup \left \{ h\right \} \right ) \setminus \mathbb {W}\left ( S\right ) $ and $A\in \mathcal {A},$ then $w\left [ A\right ] \in \mathcal {L(}S,\mathcal {A)}^{\perp }.$

We need to divide the proof by cases:

Case 50. w contains an $h.$

This case is further divided into subcases.

In case w is of the form $zh^{-1}phq$ where $z,p,q\in \mathbb {W}\left ( S\cup \left \{ h\right \} \right ) ,$ then w will contain a subword of the form $h^{-1}lh$ with $l\in \mathbb {W}\left ( S\right ) .$ By the Claim 47, we get that the image of w is finite.

Now, if this was not the case, we can find $z\in \mathbb {W}\left ( S\right ) $ and $p\in \mathbb {W}\left ( S\cup \left \{ h\right \} \right ) $ such that $w=zhp.$ In this case, the image of w is contained in $z\left [ Y\right ] .$ By Lemma 45, we know $z\left [ Y\right ] \in \mathcal {L(}S,\mathcal {A)}^{\perp },$ so the result follows.

Case 51. w does not contain an $h.$

Follows by Claim 48 since w most contain an $h^{-1}.$

We are now in position to prove that $\mathcal {L(}S\cup \left \{ h\right \} ,\mathcal {A)}$ is an AD family. Let $w,z\in \mathbb {W}\left ( S\cup \left \{ h\right \} \right ) $ and $A,B\in \mathcal {A}$ such that $w\left [ A\right ] \cap z\left [ B\right ] $ is infinite. Since words are injective, we may assume that w and z does not start in the same way, so $z^{-1}w$ is a reduced word. Since $w\left [ A\right ] \cap z\left [ B\right ] $ is infinite, we get that $z^{-1}w\left [ A\right ] \cap B$ is infinite. By Claim 49, we conclude that $z^{-1} w\in \mathbb {W}\left ( S\right ) .$ Finally, since $(S,\mathcal {A})$ is a nice pair, it follows that $w=z$ and $A=B.$

The following is well-known, we include the proof for completeness.

Lemma 52. Let $\mathcal {A}$ be an AD family of size less than $\mathfrak {b}$ and $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ \omega \right ] ^{\omega }$ pairwise disjoint such that $X_{n}\in \mathcal {A}^{\perp }$ for every $n\in \omega .$ There is an increasing function $g\in \omega ^{\omega }$ such that $\bigcup \limits _{n\in \omega }\left ( X_{n}\setminus g\left ( n\right ) \right ) \in \mathcal {A}^{\perp }.$

Proof Let $\mathcal {A}=\left \{ A_{\alpha }\mid \alpha <\kappa \right \} $ for some cardinal $\kappa $ smaller than $\mathfrak {b}.$ For every $\alpha <\mathfrak {b},$ define the function $f_{\alpha }:\omega \longrightarrow \omega $ such that $f_{\alpha }\left ( n\right ) =max\left ( A_{\alpha }\cap X_{n}\right ) +1.$ Since $\kappa <\mathfrak {b},$ we know that the family $\mathcal {B}=\left \{ f_{\alpha }\mid \alpha <\kappa \right \} $ is bounded. Any increasing function bounding $\mathcal {B}$ has the desired property.

The following will be useful for getting tight MAD families:

Proposition 53. Let $(S,\mathcal {A})$ be a good pair such that $\left \vert S\right \vert +\left \vert \mathcal {A}\right \vert <\mathfrak {b}.$ Let $\left \{ X_{n}\mid n\in \omega \right \} $ be a family pairwise disjoint infinite sets such that $X_{n}\in \mathcal {L(}S,\mathcal {A)}^{\perp }$ for every $n\in \omega .$ There are $D_{n}\in \left [ X_{n}\right ] ^{\omega }$ such that if $D=\bigcup \limits _{n\in \omega }D_{n},$ then $(S,\mathcal {A}\cup \left \{ D\right \} )$ is a nice pair.

Proof For convenience, let $\mathcal {B=L(}S,\mathcal {A)}^{\perp }.$ Since $\left \vert \mathcal {B}\right \vert <\mathfrak {b},$ by Lemma 52, we can find an increasing $g\in \omega ^{\omega }$ such that if we let $Y_{n} =X_{n}\setminus g\left ( n\right ) $ for every $n\in \omega ,$ then $Y=\bigcup \limits _{n\in \omega }Y_{n}$ is in $\mathcal {B}^{\perp }.$ Now, choose $\mathcal {P}=\left \{ P_{n}\mid n\in \omega \right \} \subseteq \left [ Y\right ] ^{\omega }$ with the following properties:

1. $\mathcal {P}$ is a partition of $Y.$
2. Each $Y_{n}$ contains infinitely many elements of $\mathcal {P}.$
3. Every element of $\mathcal {P}$ is contained in some $Y_{n}.$

In other words, $\mathcal {P}$ is obtained by dividing each $Y_{n}$ in infinitely many infinite pieces. For each $n\in \omega ,$ let $l_{n} :\omega \longrightarrow P_{n}$ be its enumerative function.

Let $w,z\in \mathbb {W}\left [ S\right ] $ be two different words. We define an associated slalom-predictor as follows:

$ \begin {array} [c]{c} \pi _{wz}:\omega ^{<\omega }\longrightarrow \left [ \omega \right ] ^{<\omega }. \end {array} $

1. $\pi _{wz}\left ( \emptyset \right ) =0.$
2. Let $t=\left \langle n_{0},\dots ,n_{m}\right \rangle .$ Define:

$ \begin {array} [c]{cccc} \pi _{wz}\left ( t\right ) & = & \left \{ n_{0},\dots ,n_{m}\right \} & \cup \\ & & l_{m}^{-1}(z^{-1}w[\left \{ l_{0}\left ( n_{0}\right ) ,\dots ,l_{m}\left ( n_{m}\right ) \right \} ]) & \cup \\ & & l_{m}^{-1}(w^{-1}z[\left \{ l_{0}\left ( n_{0}\right ) ,\dots ,l_{m}\left ( n_{m}\right ) \right \} ]). & \end {array} $

It is easy to see that there is a function $k:\omega \longrightarrow \omega $ such that each $\pi _{wz}$ is a k-slalom predictor. Since $\left \vert S\right \vert <\mathfrak {b\leq }$ non $\left ( \mathcal {M}\right ) $ by Theorem 39, we can find an injective $h:\omega \longrightarrow \omega $ that escapes from each $\pi _{wz}.$ Define $D=\left \{ l_{n}\left ( h\left ( n\right ) \right ) \mid n\in \omega \right \} $ and $D_{n}=D\cap Y_{n}$ for every $n\in \omega .$ It follows that each $D_{n}$ is infinite. Since $D\subseteq Y,$ it follows that $D\in \mathcal {B}^{\perp }.$

We now want to prove that $(S,\mathcal {A}\cup \left \{ D\right \} )$ is a nice pair. We only need to prove that $\mathcal {L(}S,\mathcal {A\cup }\left \{ D\right \} \mathcal {)}$ is an AD family. By Lemma 45, we only need to prove that if $w,z\in \mathbb {W}\left ( S\right ) $ and $w\neq z,$ then $w\left [ D\right ] \cap z\left [ D\right ] $ is finite. It is enough to prove that the set $L=\left \{ \left ( i,j\right ) \mid wl_{i}h\left ( i\right ) =zl_{j}h\left ( j\right ) \right \} $ is finite. Let $\left ( i,j\right ) \in L.$

We first consider the case in which $i\neq j.$ Without lost of generality, we may assume that $i<j.$ We get the following:

$ \begin {array} [c]{ccc} wl_{i}h\left ( i\right ) =zl_{j}h\left ( j\right ) & \implies & l_{j}h\left ( j\right ) =z^{-1}wl_{i}h\left ( i\right ) \\ & \implies & h\left ( j\right ) =l_{j}^{-1}z^{-1}wl_{i}h\left ( i\right ) \\ & \implies & h\left ( j\right ) \in l_{j}^{-1}\left ( z^{-1}w[\left \{ l_{0}h\left ( 0\right ) ,\dots ,l_{j-1}h\left ( j-1\right ) \right \} ]\right ) \\ & \implies & h\left ( j\right ) \in \pi _{zw}\left ( h\upharpoonright j\right ). \end {array} $

Since h escapes from $\pi _{zw},$ we conclude that there are only finitely many pairs $\left ( i,j\right ) $ that fall in this case.

Finally, if $i=j,$ then $w\left ( l_{i}h\left ( i\right ) \right ) =z\left ( l_{i}h\left ( i\right ) \right ) .$ Since w and z are almost disjoint, only finitely many pairs $\left ( i,j\right ) $ fall in this case. This finishes the proof.

We will use the following lemma several times:

Lemma 54. Let $(S,\mathcal {A})$ be a nice pair such that for every $X\in \mathcal {L} (S,\mathcal {A})^{+},$ there is $f:\omega \longrightarrow X$ such that $f\in S.$ The family $\mathcal {L}(S,\mathcal {A})$ is a Katětov uniform MAD family.

Proof Let $\mathcal {B}=\mathcal {L}(S,\mathcal {A}).$ Since $\mathcal {A}\neq \emptyset ,$ the hypothesis implies that every set in $\mathcal {I(B)}^{+}$ contains an element of $\mathcal {B}.$ This implies that $\mathcal {B}$ is maximal (in this way, $\mathcal {B}$ is a completely separable MAD family). We now prove that $\mathcal {B}$ is Katětov uniform.

Let $X\in \mathcal {B}^{+},$ we need to prove that $\mathcal {B}\upharpoonright X \leq _{\textsf {K}}\mathcal {B}.$ By the hypothesis, we know there is $f:\omega \longrightarrow X$ such that $f\in S.$ We will show that f is a Katětov function from $(\omega ,\mathcal {B})$ to $(X,\mathcal {B} \upharpoonright X).$ We will use Lemma 11. Let $D\in \mathcal {B}^{+},$ we need to prove that $f\left [ D\right ] \in \mathcal {B}^{+}.$ Since $\mathcal {B}$ is completely separable, there are $\left \{ A_{n}\mid n\in \omega \right \} \subseteq \mathcal {A}$ and $\left \{ w_{n}\mid n\in \omega \right \} \subseteq \mathbb {W}\left ( S\right ) $ such that $w_{n}\left [ A_{n}\right ] \subseteq D$ and each $w_{n}\left [ A_{n}\right ] $ is infinite. Without lost of generality, we may assume that either all $w_{n}$ start with $f^{-1}$ or none of them do.

In case that none of them start with $f^{-1},$ we get that $fw_{n}$ is a reduced word, so $fw_{n}\left [ A_{n}\right ] \in \mathcal {B}$ and clearly $fw_{n}\left [ A_{n}\right ] \subseteq f\left [ D\right ] $ for every $n\in \omega .$ Now assume that $w_{n}=f^{-1}z_{n}$ for some $z_{n}\in \mathbb {W}(S).$ It follows that each $z_{n}\left [ A_{n}\right ] $ has infinite intersection with $f\left [ D\right ] .$ This finishes the proof.

Let $\mathcal {P}$ be a property that MAD families may or not may have. We say that MAD families with property $\mathcal {P}$ exist generically, if every AD family of size less than $\mathfrak {c}$ can be extended to a MAD family with property $\mathcal {P}.$ In [Reference Guzmán and Hrušák32] the generic existence of several types of MAD families was studied. The generic existence of ultrafilters has been extensively studied (see, for example, [Reference Brendle and Flašková6, Reference Cancino-Manríquez11, Reference Canjar13, Reference Guzmán and Hrušák29], among others).

We can now prove the main result of the section:

Theorem 55. $\mathfrak {b=c}$ implies that tight Katětov maximal MAD families exist generically.

Proof Let $\mathcal {A}_{0}$ be an AD of size less than $\mathfrak {c}.$ Fix U and T subsets of $\mathfrak {c}$ with the following properties:

1. $\mathfrak {c}=U\cup T.$
2. $U\cap T=\emptyset .$
3. $\left \vert U\right \vert =\left \vert T\right \vert =\mathfrak {c}.$

Fix an enumeration $\left [ \omega \right ] ^{\omega }=\left \{ X_{\alpha } \mid \alpha \in U\right \} $ and $\left ( \left [ \omega \right ] ^{\omega }\right ) ^{\omega }=\{\overline {Y_{\alpha }}\mid \alpha \in T\}$ where $\overline {Y_{\alpha }}=\left \{ Y_{\alpha }\left ( n\right ) \mid n\in \omega \right \} .$ We will now recursively define $\{\mathcal {A}_{\alpha } \mid \alpha <\mathfrak {c}\}$ and $\{S_{\alpha }\mid \alpha <\mathfrak {c}\}$ such that for every $\alpha <\mathfrak {c},$ the following holds:

1. $\mathcal {A}_{0}=\mathcal {A}$ and $S_{0}=\left \{ Id\right \} .$
2. $\mathcal {A}_{\alpha }$ is an AD family and $S_{\alpha }$ is a partial cofinitary semigroup base.
3. $(\mathcal {A}_{\alpha },S_{\alpha })$ is a nice pair.
4. If $\beta <\alpha ,$ then $\mathcal {A}_{\beta }\subseteq \mathcal {A} _{\alpha }$ and $S_{\beta }\subseteq S_{\alpha }.$
5. $\left \vert \mathcal {A}_{\alpha }\right \vert +\left \vert S_{\alpha }\right \vert \leq \left \vert \mathcal {A}_{0}\right \vert +\left \vert \alpha \right \vert +\omega .$
6. If $\alpha $ is a limit ordinal, then $\mathcal {A}_{\alpha } =\bigcup \limits _{\beta <\alpha }\mathcal {A}_{\beta }$ and $S_{\alpha } =\bigcup \limits _{\beta <\alpha }S_{\beta }.$
7. If $\alpha \in T$ and each $Y_{\alpha }\left ( n\right ) \in \mathcal {I(L}\left ( S_{\alpha },\mathcal {A}_{\alpha }\right ) \mathcal {)}^{+},$ then there is $A\in \mathcal {A}_{\alpha +1}$ such that $A\cap Y_{\alpha }\left ( n\right ) $ is infinite for every $n\in \omega .$
8. If $\alpha \in U$ and $X_{\alpha }\in \mathcal {I(L(}S_{\alpha } ,\mathcal {A}_{\alpha }\mathcal {))}^{+},$ then there is $f\in S_{\alpha +1}$ such that $f:\omega \longrightarrow X_{\alpha }.$

Let $\alpha <\mathfrak {c}$ and assume we have already defined $\{(\mathcal {A} _{\xi },S_{\xi })\mid \xi \leq \alpha \}.$ We will now define $\mathcal {A} _{\alpha +1}$ and $S_{\alpha +1}$ (recall that at limit steps we just need to take unions). There are two cases to consider.

Case 56. $\alpha \in T.$

If there is $n\in \omega $ such that $Y_{\alpha }\left ( n\right ) \notin \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+},$ we just define $\mathcal {A}_{\alpha +1}=\mathcal {A}_{\alpha }$ and $S_{\alpha +1}=S_{\alpha }.$ Now, assume that $Y_{\alpha }\left ( n\right ) \in \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+}$ for every $n\in \omega .$ Since the size of $\mathcal {L}\left ( \mathcal {A} _{\alpha },S_{\alpha }\right ) $ is less than $\mathfrak {a=c},$ we can find $\left \{ Z_{n}\mid n\in \omega \right \} $ such that for every $n\in \omega ,$ the following holds:

1. $Z_{n}\subseteq Y_{\alpha }\left ( n\right ) $ is infinite.
2. $Z_{n}\in \mathcal {L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) ^{\perp }.$
3. $Z_{n}\cap Z_{m}=\emptyset $ whenever $n\neq m.$

Since both $\mathcal {A}_{\alpha }$ and $S_{\alpha }$ have size less than $\mathfrak {b=c},$ we can apply Proposition 53 and find $D\in \left [ \omega \right ] ^{\omega }$ such that D has infinite intersection with all the $Z_{n}$ and $(S_{\alpha },\mathcal {A}_{\alpha }\cup \left \{ D\right \} )$ is a nice pair. We now define $\mathcal {A}_{\alpha +1}=\mathcal {A}_{\alpha }\cup \left \{ D\right \} $ and $S_{\alpha +1}=S_{\alpha }.$

Case 57. $\alpha \in U.$

If $X_{\alpha }\notin \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+},$ we just define $\mathcal {A}_{\alpha +1} =\mathcal {A}_{\alpha }$ and $S_{\alpha +1}=S_{\alpha }.$ Assume that $X_{\alpha }\in \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+}.$ Since the size of $\mathcal {L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) $ is less than $\mathfrak {a=c},$ we can find $Z\in \left [ X\right ] ^{\omega }$ such that $Z\in \mathcal {L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) ^{\perp }.$ Moreover, we know that the size of $S_{\alpha }$ is less than non $\left ( \mathcal {M}\right ) =\mathfrak {c},$ so by Proposition 46, we know there is an injective function $f:\omega \longrightarrow Z$ such that $(S_{\alpha }\cup \left \{ f\right \} ,\mathcal {A}_{\alpha })$ is a nice pair. Define $\mathcal {A}_{\alpha +1}=\mathcal {A}_{\alpha }$ and $S_{\alpha +1}=S_{\alpha }\cup \left \{ f\right \} .$

This finishes the construction. Define $S_{\mathfrak {c}}=\bigcup \limits _{\alpha <\mathfrak {c}}S_{\alpha }$ and $\mathcal {A}_{\mathfrak {c} }=\bigcup \limits _{\alpha <\mathfrak {c}}\mathcal {A}_{\alpha }.$ It is clear that $(S_{\mathfrak {c}},\mathcal {A}_{c})$ is a nice pair. Let $\mathcal {B=L} (S_{\mathfrak {c}},\mathcal {A}_{c}).$ By Lemma 54, it follows that $\mathcal {B}$ is a Katětov uniform MAD family. It is also clear that $\mathcal {B}$ is tight. By Proposition 30, $\mathcal {B}$ is a Katětov maximal MAD family.

In [Reference Guzmán and Hrušák32], it was proved that $\mathfrak {b=c}$ is equivalent to the generic existence of tight MAD families. We conclude the following:

Corollary 58. Tight, Katětov maximal MAD families exist generically if and only if $\mathfrak {b=c}.$

If we are only interested in Katětov uniform MAD families, we can use a weaker hypothesis than the one in Theorem 55:

Theorem 59. non $\left ( \mathcal {M}\right ) =\mathfrak {a=c}$ implies that Katětov uniform MAD families exist generically.

Proof Let $\mathcal {A}$ be an AD of size less than $\mathfrak {c}.$ We can assume that $\mathcal {A}$ is at least countable. Fix an enumeration $\left [ \omega \right ] ^{\omega }=\left \{ X_{\alpha }\mid \alpha \in \mathfrak {c}\right \} .$ We will now recursively define $\{S_{\alpha }\mid \alpha <\mathfrak {c}\}$ such that for every $\alpha <\mathfrak {c},$ the following holds:

1. $S_{0}=\left \{ Id\right \} .$
2. $S_{\alpha }$ is a partial cofinitary semigroup base.
3. $(\mathcal {A},S_{\alpha })$ is a nice pair.
4. If $\beta <\alpha ,$ then $S_{\beta }\subseteq S_{\alpha }.$
5. $\left \vert \mathcal {A}\right \vert +\left \vert S_{\alpha }\right \vert \leq \left \vert \mathcal {A}\right \vert +\left \vert \alpha \right \vert +\omega .$
6. If $\alpha $ is a limit ordinal, then $S_{\alpha }=\bigcup \limits _{\beta <\alpha }S_{\beta }.$
7. If $X_{\alpha }\in \mathcal {I(L}\left ( S_{\alpha },\mathcal {A}\right ) \mathcal {)}^{+},$ then there is $f\in S_{\alpha +1}$ such that $f:\omega \longrightarrow X_{\alpha }.$

Let $\alpha <\mathfrak {c}$ and assume we have already defined $S_{\xi }$ for $\xi \leq \alpha ,$ we will now define $S_{\alpha +1}$ . We simply use the same construction as in the case that $\alpha \in U$ of Theorem 55.

Define $S=\bigcup \limits _{\alpha <\mathfrak {c}}S_{\alpha }$ . It is clear that $(S,\mathcal {A})$ is a nice pair. Let $\mathcal {B=L}(S,\mathcal {A}).$ By Lemma 54, it follows that $\mathcal {B}$ is a Katětov uniform MAD family.

The previous result was proved by García-Ferreira and Hrušák assuming $\mathfrak {t=c}$ (see [Reference Hrušák and Ferreira40]). It is worth noting that it is consistent that $\mathfrak {b<a=}$ non $\left ( \mathcal {M}\right ) =\mathfrak {c}.$ This is the case in the following models:

1. Shelah’s first model of $\mathfrak {b<a}$ (see the book [Reference Shelah60]; see also [Reference Brendle and Raghavan8, Reference Guzmán, Hrušák and Martínez-Celis31, Reference Guzmán and Kalajdzievski30]).
2. Brendle’s finite support model of $\mathfrak {b<a}$ (see [Reference Brendle5]).
3. Dow’s model in which $\mathfrak {b<s=a}$ and every compact space of countable tightness and weight $\omega _{1}$ is Fréchet (see [Reference Dow18]).
4. The model of $\mathfrak {u<a}$ in [Reference Guzmán, Hrušák, Martínez and Ramos30].

It is not clear if there are Katětov maximal MAD families in the models above. We also do not know if the generic existence of Katětov uniform MAD families is equivalent to non $\left ( \mathcal {M}\right ) =\mathfrak {a=c}.$

6 Two more constructions

One would expect that Katětov maximal MAD families are relatively high in the Katětov order. The purpose of this section is to show that, perhaps paradoxically, this might not be the case. We will look at two properties: Sacks indestructibility and Laflammeness. Both of this properties serve as measures of how high a MAD family is positioned in the Katětov order. We will show that (consistently) Katětov maximal MAD families may fail both. We will first explain why we are interesting in this two properties.

For a MAD family, being high in the Katětov order is necessary to have some sort of forcing indestructibility. For this reason, we may wonder if Katětov maximal MAD families have some indestructibility properties. We will show that (consistently) this is not the case. We will prove that it is consistent that there is a weakly tight, Katětov maximal MAD family that is destructible by Sacks forcing.

Recall from the preliminaries section, the mapping $\pi :\mathcal {P}\left ( 2^{<\omega }\right ) \longrightarrow \mathcal {P}\left ( 2^{\omega }\right ) $ is define as $\pi \left ( a\right ) =\{x\in 2^{\omega }\mid \exists ^{\infty }s\in a\left ( s\subseteq x\right ) \}.$ The ideal ctble is the ideal of all finite or countable subsets of $2^{\omega }$ and its trace ideal is defined as tr(ctble) $=\{a\subseteq 2^{\omega }\mid \pi \left ( a\right ) \in $ ctble $\}.$ Trace ideals were first introduced by Brendle. The reason we were interested in finding Katětov maximal MAD families that are destructible by Sacks forcing is because of the following (particular case of a) theorem of Brendle and Yatabe:Footnote ⁵

Theorem 60 [Reference Brendle, Spinas and Zhang9].

Let $\mathcal {A}$ be a MAD family. The following statements are equivalent $:$

1. Sacks forcing destroys $\mathcal {A}.$
2. Every forcing that adds a new real destroys $\mathcal {A}.$
3. $\mathcal {A}\leq _{\textsf {K}}$ tr(ctble).

The following property was first consider in [Reference Laflamme52] by Laflamme:

Definition 61. Let $\mathcal {A}$ be a MAD family. We say $\mathcal {A}$ is a Laflamme family if there is no $F_{\sigma }$ -ideal $\mathcal {I}$ such that $\mathcal {I}(\mathcal {A})\subseteq \mathcal {I}.$

An interesting features of non-Laflamme families is that they can be destroyed by a forcing that does not add unbounded reals (see [Reference Hernández-Hernández and Hrušák35, Reference Laflamme52, Reference Zapletal62]). Laflamme MAD families play a fundamental role in some of the proofs of the consistency of the inequality $\mathfrak {b<a}$ (see [Reference Brendle5, Reference Brendle and Raghavan8, Reference Guzmán, Hrušák and Martínez-Celis31, Reference Guzmán and Kalajdzievski30, Reference Shelah60]). In [Reference Laflamme52] Laflamme proved that CH implied that there is a Laflamme MAD family. This was later improved by Minami and Sakai in [Reference Minami and Sakai57] where they showed that $\mathfrak {p=c}$ is enough. The following result may be consider folklore:

Lemma 62. Let $\mathcal {A}$ be a MAD family. The following are equivalent $:$

1. $\mathcal {A}$ is a Laflamme MAD family.
2. There is no $F_{\sigma }$ -ideal $\mathcal {I}$ such that $\mathcal {A}$ $\leq _{\textsf {K}}\mathcal {I}.$

For this reason, Laflamme MAD families most be high in the Katětov order. Once again, we might be tempted to think that Katětov maximal MAD families must be Laflamme. We will show that this is not the case.

We will now develop some general results for constructing Katětov maximal AD families contained in a given ideal. We give two applications, but we hope there will be more applications in the future.

Lemma 63. Let $\mathcal {I}$ be a tall ideal, $(S,\mathcal {A})$ a nice pair such that $\left \vert S\right \vert <\mathfrak {h}$ and $\mathcal {L(} S,\mathcal {A)\subseteq I}.$ Let $X\in \mathcal {L(}S,\mathcal {A)}^{\perp }.$ There is an injective function $f:\omega \longrightarrow X$ such that $(S\cup \left \{ f\right \} ,\mathcal {A})$ is a nice pair and $\mathcal {L(} S\cup \left \{ f\right \} ,\mathcal {A)\subseteq I}.$

Proof For every word $w\in \mathbb {W}\left ( S\right ) ,$ define $D_{w}=\{Y\in \left [ X\right ] ^{\omega }\mid w\left [ Y\right ] \in \mathcal {I}\}.$ Since $\mathcal {I}$ is a tall ideal, it follows that each $D_{w}$ is an open dense subset of $\left [ \omega \right ] ^{\omega }.$ We know that $\left \vert S\right \vert <\mathfrak {h},$ so we can find $X_{0}\in \left [ X\right ] ^{\omega }$ such that $w\left [ X_{0}\right ] \in \mathcal {I}$ for every $w\in \mathbb {W}\left ( S\right ) .$ Now, since the size of S is less than non $\left ( \mathcal {M}\right ) ,$ we can use Proposition 40 and find $Y\in \left [ X_{0}\right ] ^{\omega }$ such that for every $w,z\in \mathbb {W}(S)$ distinct, it is the case that $w\left [ Y\right ] \cap z\left [ Y\right ] $ is finite. We now apply Proposition 43 and get an injective function $h:\omega \longrightarrow Y$ such that $S_{1}=S\cup \left \{ h\right \} $ is a partial cofinitary semigroup base. By the proof of Proposition 46, we know that $(S_{1},\mathcal {A})$ is a nice pair. It remains to prove that $\mathcal {L(}S_{1},\mathcal {A)\subseteq I}.$ The following claims were proven in Proposition 46:

Claim 64. Let $w\in \mathbb {W}\left ( S_{1}\right ) .$ If w contains a subword of the form $h^{-1}zh$ with $z\in \mathbb {W}\left ( S\right ) $ ( $z\neq Id$ ), then img $\left ( w\right ) $ is finite.

Claim 65. If $w\in \mathbb {W}\left ( S\right ) $ and $A\in \mathcal {A},$ then $h^{-1}w\left [ A\right ] $ is finite.

We will now prove that if $w\in \mathbb {W}\left ( S_{1}\right ) $ and $A\in \mathcal {A},$ then $w\left [ A\right ] \in \mathcal {I}.$ We can assume that either h or $h^{-1}$ appears in $w.$ If w does not contain $h,$ then it most contain some $h^{-1}.$ In this way, it contains a subword of the form $h^{-1}z\left [ A\right ] $ (with $z\in \mathbb {W}\left ( S\right ) )$ . It follows that $w\left [ A\right ] $ is finite and we are done. Now, assume that h appears in $w$ . If w contains a word of the form $h^{-1}zh$ with $z\in \mathbb {W}\left ( S\right ) ,$ then img $\left ( w\right ) $ is finite and we are done. If this is not the case, we can find $z\in \mathbb {W}\left ( S\right ) $ and $p\in \mathbb {W}\left ( S_{1}\right ) $ such that $w=zhp.$ In this case, we have that img $\left ( w\right ) \subseteq z\left [ Y\right ] $ and we already know that the latter is in $\mathcal {I}.$ This finishes the proof.

In order to obtain an analogue of Proposition 53, we need to introduce the following notion:

Definition 66. Let $\mathcal {I}$ be an ideal on $\omega .$ We say that $\mathcal {I}$ is cofinitary nice if for every S partial cofinitary semigroup base with $\left \vert S\right \vert <\mathfrak {c}$ and $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ \omega \right ] ^{\omega },$ there are $L\in \left [ \omega \right ] ^{\omega }$ and $\left \{ Y_{n}\mid n\in L\right \} $ with the following properties $:$

1. $Y_{n}\in \left [ X_{n}\right ] ^{\omega }$ for every $n\in L.$
2. If $w\in \mathbb {W}\left ( S\right ) $ , then $w[\bigcup \limits _{n\in L}Y_{n}]\in \mathcal {I}.$

Note that if $\mathcal {I}$ is cofinitary nice, then $\mathcal {I}$ must be a tall ideal (recall that the identity function belongs to every partial cofinitary semigroup base).

Proposition 67 ( $\mathfrak {h=c}$ ).

Let $\mathcal {I}$ be a cofinitary nice ideal. There is a weakly tight, Katětov maximal MAD family contained in $\mathcal {I}.$

Proof Fix U and W subsets of $\mathfrak {c}$ with the following properties:

1. $\mathfrak {c}=U\cup W.$
2. $U\cap W=\emptyset .$
3. $\left \vert U\right \vert =\left \vert W\right \vert =\mathfrak {c}.$

Fix an enumeration $\left [ \omega \right ] ^{\omega }=\left \{ K_{\alpha } \mid \alpha \in U\right \} $ and $\left ( \left [ \omega \right ] ^{\omega }\right ) ^{\omega }=\{\overline {U_{\alpha }}\mid \alpha \in W\}$ where $\overline {U_{\alpha }}=\left \{ U_{\alpha }\left ( n\right ) \mid n\in \omega \right \} .$ We will now recursively define $\{\mathcal {A}_{\alpha } \mid \alpha <\mathfrak {c}\}$ and $\{S_{\alpha }\mid \alpha <\mathfrak {c}\}$ such that for every $\alpha <\mathfrak {c},$ the following holds:

1. $\mathcal {A}_{0}$ is a partition of $\omega $ in countably many pieces and $S_{0}=\left \{ Id\right \} .$
2. $\mathcal {A}_{\alpha }$ is an AD family and $S_{\alpha }$ is a partial cofinitary semigroup base.
3. $(\mathcal {A}_{\alpha },S_{\alpha })$ is a nice pair.
4. $\mathcal {L}(\mathcal {A}_{\alpha },S_{\alpha })\subseteq \mathcal {I}.$
5. If $\beta <\alpha ,$ then $\mathcal {A}_{\beta }\subseteq \mathcal {A} _{\alpha }$ and $S_{\beta }\subseteq S_{\alpha }.$
6. $\left \vert \mathcal {A}_{\alpha }\right \vert +\left \vert S_{\alpha }\right \vert \leq \left \vert \alpha \right \vert +\omega .$
7. If $\alpha $ is a limit ordinal, then $\mathcal {A}_{\alpha } =\bigcup \limits _{\beta <\alpha }\mathcal {A}_{\beta }$ and $S_{\alpha } =\bigcup \limits _{\beta <\alpha }S_{\beta }.$
8. If $\alpha \in W$ and each $U_{\alpha }\left ( n\right ) \in \mathcal {I(L}\left ( S_{\alpha },\mathcal {A}_{\alpha }\right ) \mathcal {)}^{+},$ then there is $A\in \mathcal {A}_{\alpha +1}$ such that $A\cap U_{\alpha }\left ( n\right ) $ is infinite for infinitely many $n\in \omega .$
9. If $\alpha \in U$ and $K_{\alpha }\in \mathcal {I(L(}S_{\alpha } ,\mathcal {A}_{\alpha }\mathcal {))}^{+},$ then there is $f\in S_{\alpha +1}$ such that $f:\omega \longrightarrow K_{\alpha }.$

Let $\alpha <\mathfrak {c}$ and assume we have already defined $\{(\mathcal {A} _{\xi },S_{\xi })\mid \xi \leq \alpha \},$ we will now define $\mathcal {A} _{\alpha +1}$ and $S_{\alpha +1}$ . There are two cases to consider.

Case 68. $\alpha \in W.$

If there is $n\in \omega $ such that $U_{\alpha }\left ( n\right ) \notin \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+},$ we just define $\mathcal {A}_{\alpha +1}=\mathcal {A}_{\alpha }$ and $S_{\alpha +1}=S_{\alpha }.$ Now, assume that $U_{\alpha }\left ( n\right ) \in \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+}$ for every $n\in \omega .$ Since the size of $\mathcal {L}\left ( \mathcal {A} _{\alpha },S_{\alpha }\right ) $ is less than $\mathfrak {a=c},$ we can find $\left \{ X_{n}\mid n\in \omega \right \} $ such that for every $n\in \omega ,$ the following holds:

1. $X_{n}\subseteq U_{\alpha }\left ( n\right ) .$
2. $X_{n}\in \mathcal {L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) ^{\perp }.$
3. $X_{n}\cap X_{m}=\emptyset $ whenever $n\neq m.$

Since $\mathcal {I}$ is cofinitary nice $,$ we can find $L\in \left [ \omega \right ] ^{\omega }$ and $\left \{ Y_{n}\mid n\in L\right \} $ with the following properties:

1. $Y_{n}\in \left [ X_{n}\right ] ^{\omega }$ for each $n\in L.$
2. If $w\in \mathbb {W}\left ( S_{\alpha }\right ) ,$ then $w[\bigcup \limits _{n\in L}Y_{n}]\in \mathcal {I}.$

Since both $\mathcal {A}_{\alpha }$ and $S_{\alpha }$ have size less than $\mathfrak {b=c},$ we can apply Proposition 53 and find $D\subseteq \bigcup \limits _{n\in L}Y_{n}$ such that D has infinite intersection with all the $Y_{n}$ ( $n\in L$ ) and $(S_{\alpha },\mathcal {A} _{\alpha }\cup \left \{ D\right \} )$ is a nice pair. We now define $\mathcal {A}_{\alpha +1}=\mathcal {A}_{\alpha }\cup \left \{ D\right \} $ and $S_{\alpha +1}=S_{\alpha }.$

Case 69. $\alpha \in U.$

If $K_{\alpha }\notin \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+},$ we just define $\mathcal {A}_{\alpha +1} =\mathcal {A}_{\alpha }$ and $S_{\alpha +1}=S_{\alpha }.$ Assume that $K_{\alpha }\in \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+}.$ Since the size of $\mathcal {L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) $ is less than $\mathfrak {a=c},$ we can find $X\in \left [ K_{\alpha }\right ] ^{\omega }$ such that $X\in \mathcal {L}\left ( \mathcal {A} _{\alpha },S_{\alpha }\right ) ^{\perp }.$ Moreover, we know that the size of $S_{\alpha }$ is less than $\mathfrak {h}=\mathfrak {c},$ so by Lemma 63, there is an injective function $f:\omega \longrightarrow X$ such that $(S_{\alpha }\cup \left \{ f\right \} ,\mathcal {A}_{\alpha })$ is a nice pair and $\mathcal {L(}S_{\alpha }\cup \left \{ f\right \} ,\mathcal {A}_{\alpha })\subseteq \mathcal {I}$ . Define $\mathcal {A} _{\alpha +1}=\mathcal {A}_{\alpha }$ and $S_{\alpha +1}=S_{\alpha }\cup \left \{ f\right \} .$

This finishes the construction. Define $S_{\mathfrak {c}}=\bigcup \limits _{\alpha <\mathfrak {c}}S_{\alpha }$ and $\mathcal {A}_{\mathfrak {c} }=\bigcup \limits _{\alpha <\mathfrak {c}}\mathcal {A}_{\alpha }.$ It is clear that $(S_{\mathfrak {c}},\mathcal {A}_{c})$ is a nice pair. Let $\mathcal {D=L} (S_{\mathfrak {c}},\mathcal {A}_{c}).$ By Lemma 54, it follows that $\mathcal {D}$ is a Katětov uniform MAD family. It is also clear that $\mathcal {D}$ is weakly tight. By Proposition 30, $\mathcal {D}$ is a Katětov maximal MAD family contained in $\mathcal {I}.$

The Definition 66 is exactly what is needed in order to obtain Proposition 67. In practice, it is common to find an stronger property:

Definition 70. Let W be a countable set and $\mathcal {I}$ a tall ideal on $W.$

1. Define Inj $\left ( W\right ) $ as the set of all injective $g:A\longrightarrow W$ with $A\subseteq W.$
2. We say that $\mathcal {I}$ is injectively nice if for every $S\subseteq $ Inj $\left ( W\right ) $ with $\left \vert S\right \vert <\mathfrak {c}$ and $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ W\right ] ^{\omega },$ there are $L\in \left [ \omega \right ] ^{\omega }$ and $\left \{ Y_{n}\mid n\in L\right \} $ such that $:$
1. (a) $Y_{n}\in \left [ X_{n}\right ] ^{\omega }$ for every $n\in L.$
2. (b) If $f\in S,$ then $f[\bigcup \limits _{n\in L}Y_{n}]\in \mathcal {I}.$

This definition and Definition 66 are almost exactly the same, except that now we do not require a partial cofinitary semigroup base, only a set of injective partial functions.

We will now start proving that (consistently) there may be a Katětov maximal MAD family that is destructible by Sacks forcing. In order to do so, we will prove that it is consistent that tr(ctble) is injectively nice. We start with some definitions:

Definition 71. Let $A\subseteq 2^{<\omega }.$

1. Let $f\in 2^{\omega }.$ Define $\widehat {f}=\left \{ f\upharpoonright n\mid n\in \omega \right \} .$
2. Let $f,g\in 2^{\leq \omega }.$ Define $\triangle \left ( f,g\right ) = \mathrm{min} \left \{ n\mid f\left ( n\right ) \neq g\left ( n\right ) \right \} .$
3. A is a branch-set if there is $r\in 2^{\omega }$ such that $A\subseteq \widehat {r}.$
4. A is an almost branch-set if there is $F\in \left [ A\right ] ^{<\omega }$ such that $A\setminus F$ is a branch set.
5. We say that A is a comb if A is an infinite antichain and there is $r\in 2^{\omega }$ such that for every $s,t\in A,$ if $s\neq t,$ then $\triangle \left ( s,r\right ) \neq \triangle \left ( t,r\right ) .$ In this situation, we say that A is a comb with base $r.$
6. A is almost a comb if there is $F\in \left [ A\right ] ^{<\omega }$ such that $A\setminus F$ is a comb. In the same way, A is almost a comb with base r if there is $F\in \left [ A\right ] ^{<\omega }$ such that $A\setminus F$ is a comb with base $r.$

It is easy to see that a (almost) comb has a unique base. Note that every almost branch-set and every almost comb is in tr(ctble).

Lemma 72. Every infinite subset of $2^{<\omega }$ contains an infinite branch-set or a comb.

Proof By Ramsey’s Theorem, every infinite subset of $2^{<\omega }$ contains an infinite branch-set or an infinite antichain. In this way, it is enough to prove that if $B\subseteq 2^{<\omega }$ is an infinite antichain, then B contains a comb. For every $s\in B,$ define $f_{s}\in 2^{\omega }$ given by $f_{s}=s^{\frown }\overline {0}$ (where $\overline {0}$ is the constant $0$ sequence and $^{\frown }$ denotes concatenation). Since $2^{\omega }$ is compact, we can find $C\in \left [ B\right ] ^{\omega }$ and $r\in 2^{\omega }$ such that C converges to $r.$ It is easy to see that C contains a comb with base $r.$

Let $\mathcal {I}$ be an ideal on $\omega .$ Recall that an ideal $\mathcal {I}$ is $\omega $ -hitting if for every $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ \omega \right ] ^{\omega },$ there is $A\in \mathcal {I}$ such that $A\cap X_{n}$ is infinite for all $n\in \omega .$ The class of $\omega \,$ -hitting ideals has been extensively studied in the past and has many applications (see [Reference Brendle and Hrušák7, Reference Chodounský, González and Hrušák15, Reference Dow17, Reference Hrušák39, Reference Hrušák and Minami41, Reference Hrušák and Ramos-García42, Reference Michael, Meza-Alcántara, Thümmel and Uzcátegui55]). It is easy to see that tr(ctble) is not $\omega $ -hitting: If $D\subseteq 2^{\omega }$ is any countable dense set, then the family $\{\widehat {d}\mid d\in D\}$ witnesses that tr(ctble) is not $\omega $ -hitting. However, we will see that it satisfies a weaker property.

Definition 73. Let $\mathcal {I}$ be an ideal on $\omega .$ We say that $\mathcal {I}$ is weakly $\omega $ -hitting, if for every $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ \omega \right ] ^{\omega },$ there is $A\in \mathcal {I}$ such that $A\cap X_{n}$ is infinite for infinitely many $n\in \omega .$

The following lemma will be helpful:

Lemma 74. Let $\left \{ A_{n}\mid n\in \omega \right \} $ be a family of antichains of $2^{<\omega }, r\in 2^{\omega }$ and $\left \{ r_{n}\mid n\in \omega \right \} \subseteq 2^{\omega }$ such that for every $n\in \omega ,$ the following holds $:$

1. $A_{n}$ is a comb with base $r_{n}.$
2. The sequence $\left \langle r_{n}\right \rangle _{n\in \omega }$ converges to $r.$
3. $r\neq r_{n}.$
4. If $s\in A_{n},$ then $\triangle \left ( s,r_{n}\right )>\triangle \left ( s,r\right ) .$

Then $\pi (\bigcup \limits _{n\in \omega }A_{n})=\emptyset .$ In particular, $\bigcup \limits _{n\in \omega }A_{n}\in $ tr(ctble).

Proof Let $B=\bigcup \limits _{n\in \omega }A_{n}$ and note that $\widehat {r}\cap B=\emptyset ,$ so $r\notin \pi (B).$ Pick $x\in 2^{\omega },$ we need to prove that $x\notin \pi \left ( B\right ) .$ We can already assume that $x\neq r.$ Since each $A_{i}$ is an antichain, it follows that $\widehat {x}\cap A_{i}$ is finite. In order to prove that $x\notin \pi \left ( B\right ) ,$ it is enough to prove that there are only finitely many $n\in \omega $ for which $\widehat {x}\cap A_{n}\neq \emptyset .$

Let $n\in \omega $ such that $\widehat {x}\cap A_{n}\neq \emptyset $ and define $k=\triangle \left ( x,r\right ) .$ Choose any $s\in \widehat {x}\cap A_{n}.$ Since $s\notin \widehat {r},$ it follows that

$ \begin {array} [c]{ccc} k & = & \triangle \left ( x,r\right ) \\ & = & \triangle \left ( s,r\right ) \\ & < & \triangle \left ( s,r_{n}\right ). \end {array} $

Hence $\triangle \left ( r,r_{n}\right ) =k.$ Since $\left \langle r_{i}\right \rangle _{i\in \omega }$ converges to $r,$ it follows that there are only finitely many possibilities for $n.$

The following is a similar lemma:

Lemma 75. Let $\left \{ A_{n}\mid n\in \omega \right \} $ be a set of antichains of $2^{<\omega }$ and $r\in 2^{\omega }$ such that each $A_{n}$ is a comb with base $r.$ If for every $n\in \omega $ and $s\in A_{n}$ we have that $\triangle \left ( s,r\right )>n,$ then $\pi (\bigcup \limits _{n\in \omega }A_{n})=\emptyset $ (so $\bigcup \limits _{n\in \omega }A_{n}\in $ tr(ctble)).

Proof Let $B=\bigcup \limits _{n\in \omega }A_{n}$ . As before, $\widehat {r}\cap B=\emptyset ,$ so $r\notin \pi (B).$ Let $x\in 2^{\omega },$ we need to prove that $x\notin \pi \left ( B\right ) .$ As in the lemma before, we can already assume that $x\neq r$ and it is enough to prove that there are only finitely many $n\in \omega $ for which $\widehat {x}\cap A_{n}\neq \emptyset .$

Let $n\in \omega $ such that $\widehat {x}\cap A_{n}\neq \emptyset $ and define $k=\triangle \left ( x,r\right ) .$ By our hypothesis, we conclude that $n<k.$ Therefore, there are only finitely many possibilities for $n.$

With this results we can prove the following proposition. Strictly speaking, it will not be needed in the rest of the paper, but it is a good warm-up for the following arguments.

Proposition 76. The ideal tr(ctble) is weakly $\omega $ -hitting.

Proof Let $\mathcal {A}=\left \{ A_{n}\mid n\in \omega \right \} \subseteq \left [ 2^{<\omega }\right ] ^{\omega }.$ By shrinking each $A_{n}$ and passing to an infinite subset of $\mathcal {A}$ , we may assume that either every $A_{n}$ is a branch-set or every $A_{n}$ is a comb (see Lemma 72). We divide the proof by cases:

Case 77. Each $A_{n}$ is a branch-set.

For every $n\in \omega ,$ let $r_{n}\in 2^{\omega }$ such that $A_{n}\subseteq \widehat {r}_{n}.$ If there is $r\in 2^{\omega }$ such that there are infinitely many $n\in \omega $ for which $r=r_{n},$ then $\widehat {r}$ intersects infinitely many elements of $\mathcal {A}.$ Assume this is not the case. Since $2^{\omega }$ is compact, we can find $W\in \left [ \omega \right ] ^{\omega }$ such that $\left \{ r_{n}\mid n\in W\right \} $ is a converging sequence. Let $B=\bigcup \limits _{n\in W}\widehat {r}_{n}.$ It is clear that $\pi \left ( B\right ) $ is countable, so $B\in $ tr(ctble) and B has infinite intersection with infinitely many elements of $\mathcal {A}.$

Case 78. Each $A_{n}$ is a comb.

For every $n\in \omega ,$ let $r_{n}\in 2^{\omega }$ such that $A_{n}$ is a comb with base $r_{n}.$ First consider the case where there is $r\in 2^{\omega }$ such that there are infinitely many $n\in \omega $ for which $r=r_{n}.$ Let $W=\left \{ n\in \omega \mid r_{n}=r\right \} .$ For every $n\in \omega ,$ we can find $B_{n}\in \left [ A_{n}\right ] ^{\omega }$ such that for every $s\in B_{n},$ we have that $\triangle \left ( s,r\right )>n.$ By Lemma 75, it follows that $\bigcup \limits _{n\in W}B_{n}\in $ tr(ctble) and we are done.

Now assume there is no such $r.$ Since $2^{\omega }$ is compact, we can find $y\in 2^{\omega }$ and $Z\in \left [ \omega \right ] ^{\omega }$ such that $\left \{ r_{n}\mid n\in Z\right \} $ converges to y and $y\neq r_{n}$ for every $n\in Z.$ We can now find $B_{n}\in \left [ A_{n}\right ] ^{\omega }$ (for $n\in Z$ ) such that for every $s\in B,$ it is the case that $\triangle \left ( s,r_{n}\right )>\triangle \left ( s,r\right ) .$ By Lemma 74, we know that $\bigcup \limits _{n\in Z}B_{n}\in $ tr(ctble) and we are done.

We will now prove that tr(ctble) may be injectively nice:

Proposition 79 ( $\mathfrak {h=c}$ ).

tr(ctble) is injectively nice.

Proof Let $S\subseteq $ Inj $\left ( 2^{<\omega }\right ) $ of size less that $\mathfrak {c}$ and $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ 2^{<\omega }\right ] ^{\omega }.$ Since $\left \vert S\right \vert <\mathfrak {h}$ and with the aid of Lemma 72, we can find $\left \{ Z_{n}\mid n\in \omega \right \} $ with the following properties:

1. $Z_{n}\in \left [ X_{n}\right ] ^{\omega }$ for every $n\in \omega .$
2. If $w\in S$ and $n\in \omega ,$ then $w\left [ Z_{n}\right ] $ is an almost branch-set or an almost comb.

Let $w\in S,$ define the following sets:

1. $D_{0}\left ( w\right ) $ is the set of all $E\in \left [ \omega \right ] ^{\omega }$ for which there are $r\in 2^{\omega }, n\in \omega $ and $\left \{ r_{i}\mid i\in E\wedge i>n\right \} \subseteq 2^{\omega }$ such that for every $i,j\in E$ with $n<i,j,$ the following conditions hold:
1. (a) $w\left [ Z_{i}\right ] $ is an almost comb with base $r_{i}.$
2. (b) $r_{i}\neq r.$
3. (c) If $i\neq j,$ then $r_{i}\neq r_{j}.$
4. (d) $\left \{ r_{l}\mid l\in E\wedge l>n\right \} $ converges to $r.$
2. $D_{1}\left ( w\right ) $ is the set of all $E\in \left [ \omega \right ] ^{\omega }$ for which there are $r\in 2^{\omega }$ and $n\in \omega $ such that if $i\in E$ and $i>n,$ then $w\left [ Z_{i}\right ] $ is an almost comb with base $r.$
3. $D_{2}\left ( w\right ) $ is the set of all $E\in \left [ \omega \right ] ^{\omega }$ for which there are $d\in 2^{\omega }$ and $n\in \omega $ such that if $i\in E$ and $i>n,$ then $w\left [ Z_{i}\right ] \subseteq ^{\ast }\widehat {d}.$
4. $D_{3}\left ( w\right ) $ is the set of all $E\in \left [ \omega \right ] ^{\omega }$ for which there are $d\in 2^{\omega }, n\in \omega $ and $\left \{ d_{i}\mid i\in E\wedge i>n\right \} \subseteq 2^{\omega }$ such that for every $i,j\in E$ with $n<i,j,$ the following conditions hold:
1. (a) $w\left [ Z_{i}\right ] \subseteq ^{\ast }\widehat {d}_{i}.$
2. (b) $d_{i}\neq d.$
3. (c) If $i\neq j,$ then $d_{i}\neq d_{j}.$
4. (d) $\left \{ d_{l}\mid l\in E\wedge l>n\right \} $ converges to $d.$

It follows that each $D_{i}\left ( w\right ) $ is open in $\left [ \omega \right ] ^{\omega }$ (for $i<4$ ) and $D\left ( w\right ) =\bigcup \limits _{i<4}D_{i}\left ( w\right ) $ is an open dense subset of $\left [ \omega \right ] ^{\omega }.$ Now, since $\left \vert S\right \vert <\mathfrak {h},$ we can find $L\in \bigcap \limits _{w\in S}D\left ( w\right ) .$ For every $w\in S,$ we will define a function $f_{w}:L\longrightarrow \left [ 2^{<\omega }\right ] ^{<\omega }$ as follows:

Case 80. $L\in D_{0}\left ( w\right ) .$

Let $r\in 2^{\omega }, n\in \omega $ and $\left \{ r_{i}\mid i\in L\wedge i>n\right \} \subseteq 2^{\omega }$ witnessing that $L\in D_{0}\left ( w\right ) .$ Pick $m\in L.$

1. If $m\leq n,$ then $f_{w}\left ( m\right ) =\emptyset .$
2. If $m>n,$ then $f_{w}\left ( m\right ) $ has the following properties:
1. (a) $w\left [ Z_{m}\setminus f_{w}\left ( m\right ) \right ] $ is a comb with base $r_{m}.$
2. (b) If $s\in Z_{m}\setminus f_{w}\left ( m\right ) ,$ then $\triangle \left ( w\left ( s\right ) ,r_{m}\right )>\triangle \left ( w\left ( s\right ) ,r\right ) .$

Case 81. $L\in D_{1}\left ( w\right ) .$

Let $r\in 2^{\omega }$ and $n\in \omega $ witnessing that $L\in D_{1}\left ( w\right ) .$ Pick $m\in L.$

1. If $m\leq n,$ then $f_{w}\left ( m\right ) =\emptyset .$
2. If $m>n,$ then $f_{w}\left ( m\right ) $ has the following properties:
1. (a) $w\left [ Z_{m}\setminus f_{w}\left ( m\right ) \right ] $ is a comb with base $r.$
2. (b) If $s\in Z_{m}\setminus f_{w}\left ( m\right ) ,$ then $\triangle \left ( w\left ( s\right ) ,r\right )>m.$

Case 82. $L\in D_{2}\left ( w\right ) .$

Let $d\in 2^{\omega }$ and $n\in \omega $ witnessing that $L\in D_{2}\left ( w\right ) .$ Pick $m\in L.$

1. If $m\leq n,$ then $f_{w}\left ( m\right ) =\emptyset .$
2. If $m>n,$ then $f_{w}\left ( m\right ) $ is such that $w\left [ Z_{m}\setminus f_{w}\left ( m\right ) \right ] \subseteq \widehat {d}.$

Case 83. $L\in D_{3}\left ( w\right ) .$

Let $d\in 2^{\omega }, n\in \omega $ and $\left \{ d_{i}\mid i\in E\wedge i>n\right \} \subseteq 2^{\omega }$ witnessing that $L\in D_{3}\left ( w\right ) .$ Pick $m\in L.$

1. If $m\leq n,$ then $f_{w}\left ( m\right ) =\emptyset .$
2. If $m>n,$ then $f_{w}\left ( m\right ) $ has the following properties:
1. (a) $w\left [ Z_{m}\setminus f_{w}\left ( m\right ) \right ] \subseteq \widehat {d}_{m}.$
2. (b) If $s\in Z_{m}\setminus f_{w}\left ( m\right ) ,$ then $\triangle \left ( w\left ( s\right ) ,d\right ) =\triangle \left ( d,d_{m}\right ) .$

Since $\left \vert S\right \vert <\mathfrak {b},$ we can find a function $g:L\longrightarrow \left [ 2^{<\omega }\right ] ^{<\omega }$ such that for every $w\in S,$ it is the case that $f_{w}\left ( m\right ) \subseteq g\left ( m\right ) $ for almost all $m\in L.$ Given $m\in L,$ define $Y_{m} =Z_{m}\setminus g\left ( m\right ) .$ We claim that this are the items we were looking for. We need to prove that if $w\in S,$ then $w[\bigcup \limits _{n\in L}Y_{n}]\in $ tr(ctble).

Given $W\subseteq L,$ define $\overline {W}=\bigcup \limits _{n\in W}Y_{n}.$ Let $w\in S,$ our task is to show that $w\left [ \overline {L}\right ] $ is in tr(ctble). We proceed by cases:

Case 84. $L\in D_{0}\left ( w\right ) .$

Let $r\in 2^{\omega }, n\in \omega $ and $\left \{ r_{i}\mid i\in L\wedge i>n\right \} \subseteq 2^{\omega }$ witnessing that $L\in D_{0}\left ( w\right ) .$ Now, find $k\in \omega $ such that $k>n$ and $f_{w}\left ( m\right ) \subseteq g\left ( m\right ) $ for every $m\geq k.$ Define $W=L\setminus k.$ We know that $w\left [ Y_{i}\right ] \in $ tr(ctble) for all $i\in L,$ so in order to prove that $w\left [ \overline {L}\right ] \in $ tr(ctble), it is enough to show that $w\left [ \overline {W}\right ] \in $ tr(ctble).

We know that $w\left [ \overline {W}\right ] =\bigcup \left \{ w\left [ Y_{m}\right ] \mid m\in W\right \} .$ Now, if $m\in W,$ then $f_{w}\left ( m\right ) \subseteq g\left ( m\right ) ,$ which implies that $Y_{m} =Z_{m}\setminus g\left ( m\right ) \subseteq Z_{m}\setminus f_{w}\left ( m\right ) ,$ so $w\left [ Y_{m}\right ] $ is a comb with base $r_{m}.$ By Lemma 74, it follows that $w\left [ \overline {W}\right ] \in $ tr(ctble).

Case 85. $L\in D_{1}\left ( w\right ) .$

Let $r\in 2^{\omega }$ and $n\in \omega $ witnessing that $L\in D_{1}\left ( w\right ) .$ Now, find $k\in \omega $ such that $k>n$ and $f_{w}\left ( m\right ) \subseteq g\left ( m\right ) $ for every $m\geq k.$ Define $W=L\setminus k.$ It is enough to prove that $w\left [ \overline {W}\right ] \in $ tr(ctble).

We know that $w\left [ \overline {W}\right ] =\bigcup \left \{ w\left [ Y_{m}\right ] \mid m\in W\right \} .$ Moreover, if $m\in W,$ then $Y_{m}\subseteq Z_{m}\setminus f_{w}\left ( m\right ) ,$ so $w\left [ Y_{m}\right ] $ is a comb with base $r.$ By Lemma 75, it follows that $w\left [ \overline {W}\right ] \in $ tr(ctble).

Case 86. $L\in D_{2}\left ( w\right ) .$

Let $d\in 2^{\omega }$ and $n\in \omega $ witnessing that $L\in D_{2}\left ( w\right ) .$ Find $k\in \omega $ such that $k>n$ and $f_{w}\left ( m\right ) \subseteq g\left ( m\right ) $ for every $m\geq k.$ Define $W=L\setminus k.$ It is enough to prove that $w\left [ \overline {W}\right ] \in $ tr(ctble). This is trivial since $w\left [ \overline {W}\right ] \subseteq \widehat {d}.$

Case 87. $L\in D_{3}\left ( w\right ) .$

Let $d\in 2^{\omega }, n\in \omega $ and $\left \{ d_{i}\mid i\in L\wedge i>n\right \} \subseteq 2^{\omega }$ witnessing that $L\in D_{3}\left ( w\right ) .$ Find $k\in \omega $ such that $k>n$ and $f_{w}\left ( m\right ) \subseteq g\left ( m\right ) $ for every $m\geq k.$ It is enough to prove that $w\left [ \overline {W}\right ] \in $ tr(ctble). This is easy because $w[\overline {W}]\subseteq \bigcup \{\widehat {d}_{i}\mid i\in L\wedge i>n\}.$

This finishes the proof.

By combining Propositions 67 and 79 and Theorem 60, we conclude the following:

Corollary 88. $\mathfrak {h=c}$ implies that there is a weakly tight, Katětov maximal MAD family that is $\mathbb {S}\,$ -destructible.

We can now answer an open question posed in [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1]. Until now, the only known Katětov maximal MAD families were tight. This lead Arciga, Hrušák, and Martínez to ask the following:

Problem 89 (Arciga, Hrušák, and Martínez).

Does there exist a MAD family maximal in the Katětov order that is weakly tight but not tight?

The MAD family of Corollary 88 is such an example. Since it is Sacks destructible, it is also Cohen destructible, hence it can not be tight.

A trivial consequence of Corollary 88, is that $\mathfrak {h=c}$ implies that there is a MAD family such that all MAD families Katětov above it are Sacks destructible. We do not know if this is always the case.

Problem 90. Is the statement “For every MAD family $\mathcal {A},$ is there is a Sacks indestructible MAD family $\mathcal {B}$ such that $\mathcal {A}\leq _{\textsf {K}}\mathcal {B} $ ” consistent? What about for Cohen indestructibility?

We now turn our attention to Laflamme MAD families. We start with the following definition:

Definition 91

1. Let $\varphi :\mathcal {P}\left ( \omega \right ) \longrightarrow \mathbb {R\cup }\left \{ \infty \right \} $ such that if $A\subseteq \omega ,$ then $\varphi \left ( A\right ) =\sum \limits _{n\in A}\frac {1}{n+1}.$
2. The summable ideal is $\mathcal {J}_{\frac {1}{n} }=\{A\subseteq \omega \mid \varphi \left ( A\right ) <\infty \}.$

It is easy to see that $\mathcal {J}_{\frac {1}{n}}$ is a tall $F_{\sigma } $ -ideal. This ideal (and its generalizations) have been extensively studied in the past. To learn more, the reader may consult [Reference Cancino-Manríquez12, Reference Farah21, Reference Flašková25, Reference Flašková24, Reference Guzmán-González and Meza-Alcántara33, Reference Hernández-Hernández and Hrušák35, Reference Hrušák39, Reference Hrušák and Minami41]. We now proceed to prove the following:

Proposition 92 ( $\mathfrak {h=c}$ ).

The summable ideal $\mathcal {J}_{\frac {1}{n}}$ is injectively nice.

Proof Let $S\subseteq $ Inj $\left ( \omega \right ) $ of size less that $\mathfrak {c}$ and $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ \omega \right ] ^{\omega }.$ Since $\left \vert S\right \vert <\mathfrak {h},$ for all $n\in \omega $ we can find $Z_{n}\in \left [ X_{n}\right ] ^{\omega }$ with the property that $\varphi (w\left [ Z_{n}\right ] )\in \mathcal {J}_{\frac {1} {n}}.$ For every $w\in S,$ define the function $f_{w}:\omega \longrightarrow \omega $ such that for any $n\in \omega ,$ we choose $f_{w}\left ( n\right ) $ big enough so that $\varphi (w\left [ Z_{n}\right ] \diagup f_{w}\left ( n\right ) )<\frac {1}{2^{n+1}}.$ This is possible since each $\varphi (w\left [ Z_{n}\right ] )$ is in the summable ideal.

Since S has size less than $\mathfrak {b},$ we can find an increasing function $g\in \omega ^{\omega }$ dominating each $f_{w}.$ For every $n\in \omega $ let $Y_{n}=Z_{n}\setminus g\left ( n\right ) $ and $Y=\bigcup \limits _{n\in \omega }Y_{n}.$ It is easy to see that $w\left [ Y\right ] \in \mathcal {J} _{\frac {1}{n}}$ for every $w\in S.$

By combining Propositions 67 and 92, we get the following:

Corollary 93. $\mathfrak {h=c}$ implies that there is a weakly tight, Katětov maximal MAD family contained in the summable ideal. In particular, there is a Katětov maximal MAD family that is not Laflamme.

The attentive reader will note that the proofs of Propositions 67 and 92 actually show that the MAD family above can constructed to be tight, not just weakly tight. In [Reference Hernández-Hernández and Hrušák35], it was proved that $\mathcal {J}_{\frac {1}{n}}$ is Random indestructible (see [Reference Bartoszyński and Judah3] for the definition and main properties of Random forcing). In this way, $\mathfrak {h=c}$ implies that there is a Katětov maximal MAD family that is Cohen indestructible and Random destructible. Ideals and MAD families that are indestructible under some forcings but destructible with another have been studied in [Reference Brendle and Yatabe9, Reference Hrušák and Ferreira40].

7 The Cohen model

In a private communication, Michael Hrušák suggested to us to investigate if there is a Katětov maximal MAD family of size $\omega _{1}$ in the Cohen model. At first, the author believed that the parametrized diamond $\Diamond ($ non $\left ( \mathcal {M}\right ) )$ (see [Reference Moore, Hrušák and Džamonja58]) might imply that there is such a family, but we were unable to prove it. We then tried to use CH to construct a Katětov maximal MAD family that would remain Katětov maximal after adding Cohen reals, but this also failed. Finally, we realized that there are no small Katětov maximal MAD families in the Cohen model. In this section we present the proof.

In this paper, the incarnation of Cohen forcing we choose to use is $\mathbb {C}=2^{<\omega }$ ordered by extension. If $G\subseteq \mathbb {C}$ is a generic filter, the associated Cohen real is $\left \{ n\in \omega \mid \bigcup G\left ( n\right ) =1\right \} .$ If $\kappa $ is a cardinal, denote by $\mathbb {C}_{\kappa }$ the finite support product of $\kappa $ copies of $\mathbb {C}.$ Given $X\subseteq \kappa ,$ by $\mathbb {C}_{X}$ denote $\prod \limits _{\alpha \in X}^{FS}\mathbb {C}$ and we view it as a suborder of $\mathbb {C}_{\kappa }.$ It is well known that if a MAD family is $\mathbb {C}$ -indestructible, then it is $\mathbb {C}_{\kappa }$ -indestructible for every cardinal $\kappa .$

Let $\mathcal {A}$ be an AD family and $B\in \mathcal {I(A)}.$ We say that B is $\mathcal {A}$ -saturated if there are $A_{0},\dots ,A_{n} \in \mathcal {A}$ such that $B=A_{0}\cup \dots \cup A_{n}.$ Note that if B is $\mathcal {A}$ -saturated, then $B=\bigcup \{A\in \mathcal {A}\mid \left \vert A\cap B\right \vert =\omega \}.$ Given $D\in \mathcal {I}(\mathcal {A}),$ we say that B is the $\mathcal {A}$ -saturation of D if $B=\bigcup \{A\in \mathcal {A}\mid \left \vert A\cap D\right \vert =\omega \}.$ It is easy to see that if B is the $\mathcal {A}$ -saturation of $D,$ then $D\setminus B$ is finite.

Proposition 94. Let $\mathcal {A}$ and $\mathcal {B}$ two $\mathbb {C}$ -indestructible MAD families and $\kappa $ a regular cardinal. If $\dot {C}_{gen}$ is the $\mathbb {C}_{\kappa }$ -name of the Cohen generic real added by the first component, then $\mathbb {C}_{\kappa }\Vdash $ “ $\mathcal {A} \upharpoonright \dot {C}_{gen} \nleq _{\textsf {SK}} \mathcal {B} $ .”

Proof First note that $\dot {C}_{gen}$ is forced to be in $\mathcal {I(A)}^{+},$ since the Cohen generic real has infinite intersection with every ground model infinite subset of $\omega .$ We also know that both $\mathcal {A}$ and $\mathcal {B}$ remain MAD families. We argue by contradiction, assume there is a condition $\overline {p}$ and $\dot {g}$ a $\mathbb {C}_{\kappa }$ -name for a function such that $\overline {p}$ forces that $\dot {g}$ is a strong Katětov function from $(\omega ,\mathcal {B)}$ to $(\dot {C}_{gen} ,\mathcal {A}\upharpoonright \dot {C}_{gen}).$ By standard forcing arguments, we can find $Z\in \left [ \kappa \right ] ^{\omega }$ such that $\overline {p} \in \mathbb {C}_{Z}$ and both $\dot {C}_{gen}$ and $\dot {g}$ are $\mathbb {C}_{Z}$ -names.

Claim 95. There are $p\in \mathbb {C}_{Z}$ , $\mathcal {B}_{1}\in \lbrack \mathcal {B} ]^{\omega _{1}}, s,t\in \left [ \omega \right ] ^{<\omega }$ and a family $\{(A_{B},D_{B})\mid B\in \mathcal {B}_{1}\}$ with the following properties $:$

1. $p\leq \overline {p}.$
2. $A_{B}\in \mathcal {I(A)}$ and is $\mathcal {A}$ -saturated.
3. If $B\in \mathcal {B}_{1},$ then $p\Vdash $ “ $A_{B}$ is the $\mathcal {A}$ -saturation of $\dot {g}[B]$ ” and $p\Vdash $ “ $\dot {g}\left [ B\right ] \setminus A_{B}=s$ ” (so $p\Vdash $ “ $\dot {g}\left [ B\right ] \subseteq A_{B}\cup s$ ”) $.$
4. $D_{B}\in \mathcal {I(B)}$ and is $\mathcal {B}$ -saturated.
5. If $B\in \mathcal {B}_{1},$ then $p\Vdash $ “ $D_{B}$ is the $\mathcal {B}$ -saturation of $\dot {g}^{-1}(A_{B}\cup s)$ ” and $p\Vdash $ “ $\dot {g}^{-1} (A_{B}\cup s)\setminus D_{B} =t$ ” (so $p\Vdash $ “ $\dot {g}^{-1}(A_{B}\cup s)\subseteq D_{B}\cup t$ ”) $.$
6. The family $\{A_{B}\mid B\in \mathcal {B}_{1}\}$ is almost disjoint.
7. If $p_{0}$ is the first coordinate of $p,$ then $s\subseteq p_{0} ^{-1}\left ( \left \{ 1\right \} \right ) .$

We prove the claim. For every $B\in \mathcal {B}$ we find $p_{B}\in \mathbb {C}_{Z}$ , $s_{B}, t_{B}\in \left [ \omega \right ] ^{<\omega }$ and $A_{B},D_{B}$ that satisfy 1 to 5 above (with $p_{B}$ instead of p, $s_{B}$ instead of s and $t_{B}$ instead of t). Since $\mathbb {C}_{Z}$ is countable and $\mathcal {B}$ is uncountable, we can find $\mathcal {B}_{2} \in \mathcal {[B]}^{\omega _{1}}$ and $p\in \mathbb {C}_{Z}, s,t\in \left [ \omega \right ] ^{<\omega }$ such that if $B\in \mathcal {B}_{2},$ then $p_{B}=p,$ $s_{B}=s$ , and $t_{B}=t.$ Note that since p forces that s is contained in the image of $\dot {g},$ it follows that $s\subseteq p_{0}^{-1}\left ( \left \{ 1\right \} \right ) $ (where $p_{0}$ is the first coordinate of p). We got all the points of the claim, except possibly point 6.

For every $B\in \mathcal {B}_{2},$ define $F_{B}=\{E\in \mathcal {A\mid }\left \vert A_{B}\cap E\right \vert =\omega \}.$ We know that $A_{B}=\bigcup F_{B},$ each $F_{B}$ is finite and p forces that every element of $F_{B}$ has infinite intersection with $\dot {g}\left [ B\right ] .$ We now look at the set $\{F_{B}\mid B\in \mathcal {B}_{2}\}.$ We can apply the Delta System Lemma (see [Reference Kunen50]) and find $\mathcal {B}_{1}\in \lbrack \mathcal {B}_{2}]^{\omega _{1} }$ and $R\subseteq \mathcal {A}$ finite such that $\{F_{B}\mid B\in \mathcal {B}_{1}\}$ is a delta system with root $R.$ However, we claim that R is in fact the empty set. Suppose this is not the case, choose $E\in R.$ As mentioned before, it follows that $p\Vdash $ “ $\dot {g}[B]\cap E$ is infinite” for every $B\in \mathcal {B}_{1}.$ In this way, p forces that $\dot {g}^{-1}\left ( E\right ) $ has infinite intersection with uncountably many elements of $\mathcal {B},$ which is a contradiction since $\dot {g}$ is forced to be a Katětov function. We conclude that $R=\emptyset $ and this finishes the proof of the claim.

We continue with the proof. Define the function $g^{+}:\omega \longrightarrow \mathcal {P}\left ( \omega \right ) $ where In this way, $g^{+}\left ( n\right ) $ is the set of all possible values of $\dot {g}\left ( n\right ) $ (under the condition p). For every $B\in \mathcal {B}_{1}$ and $n\in \omega ,$ we have the following remarks:

*) If $n\in B,$ then $g^{+}\left ( n\right ) \subseteq A_{B}\cup s.$
**) If $n\notin D_{B}\cup t,$ then $g^{+}\left ( n\right ) \cap (A_{B}\cup s)=\emptyset .$

In order to prove the first point, note that if $n\in B,$ then $p\Vdash $ “ $\dot {g}\left ( n\right ) \in \dot {g}[B]\subseteq A_{B}\cup s,$ ” so $g^{+}\left ( n\right ) \subseteq A_{B}\cup s.$ For the second point, if $n\notin D_{B}\cup t,$ then $p\Vdash $ “ $n\notin D_{B}\cup t,$ ” so $p\Vdash $ “ $n\notin \dot {g}^{-1}(A_{B}\cup s).$ ” It follows that $p\Vdash $ “ $g\left ( n\right ) \notin A_{B}\cup s$ ,” which implies that $g^{+}\left ( n\right ) \cap (A_{B}\cup s)=\emptyset .$

Define $Y=\{n\mid g^{+}\left ( n\right ) \in \left [ \omega \right ] ^{<\omega }\}.$ We will now prove the following:

Claim 96. The set $\{B\in \mathcal {B}_{1}\mid B\cap (\omega \setminus Y)\neq \emptyset \}$ is at most countable.

We will prove something much stronger: we will show that if $n\notin Y,$ then there is at most one element of $\mathcal {B}_{1}$ that has contains $n.$ Assume this is not the case, so there is $n\notin Y$ and $B_{1},B_{2}\in Y$ for which $n\in B_{1}\cap B_{2}.$ By point *) above, it follows that $g^{+}\left ( n\right ) \subseteq \left ( A_{B_{1}}\cup s\right ) \cap \left ( A_{B_{2}}\cup s\right ) .$ But this is a contradiction, since $A_{B_{1}}$ and $A_{B_{2}}$ are almost disjoint, yet $g^{+}\left ( n\right ) $ is infinite. This finishes the proof of the claim.

Define $u=\{i\in p_{0}^{-1}\left ( \left \{ 1\right \} \right ) \mid \exists B\in \mathcal {B}_{1}\left ( i\in A_{B}\cup s\right ) \}.$ For each $i\in u,$ choose $B_{i}\in \mathcal {B}_{1}$ such that $i\in A_{B_{i}}\cup s.$ Define $A=\bigcup \limits _{i\in u}\left ( A_{B_{i}}\cup s\right ) $ and $B=\bigcup \limits _{i\in u}\left ( D_{B_{i}}\cup t\right ) .$

Claim 97. $p\Vdash $ “ $\dot {g}^{-1}\left ( u\right ) \subseteq B$ .”

We have the following:

Since $u\subseteq A,$ it follows that $p\Vdash $ “ $\dot {g} ^{-1}\left ( u\right ) \subseteq B$ .”

We know that $\mathcal {B}_{1}$ is uncountable, so appealing to the Claim 96 we can find $R\in \mathcal {B}_{1}$ with the following properties:

1. $R\subseteq Y.$
2. R and B are almost disjoint.

Choose any $n\in R\setminus B$ and pick any $l>max\left ( g^{+}\left ( n\right ) \right ) ,$ dom $\left ( p_{0}\right ) $ (recall that $n\in Y,$ so $g^{+}\left ( n\right ) $ is finite). Now, define $q\in \mathbb {C}_{Z}$ such that $q\leq p$ and if $q_{0}$ is the first component of $q,$ then dom $\left ( q\left ( 0\right ) \right ) =l$ and if $i\in l\setminus $ dom $\left ( p_{0}\right ) ,$ then $q_{0}\left ( i\right ) =0.$ It follows that $q\Vdash $ “ $\dot {C}_{gen}\cap l=p_{0}^{-1}\left ( \left \{ 1\right \} \right ) $ .” Note that $q\Vdash $ “ $\dot {g}\left ( n\right ) \in \dot {C}_{gen}\cap l$ ” ( $\dot {g}\left ( n\right ) $ is forced to be in l since $g^{+}\left ( n\right ) \subseteq l$ ). In this way, it follows that $q\Vdash $ “ $\dot {g}\left ( n\right ) \in p_{0}^{-1} (\{1\})$ .”

Now we find $r\leq q$ and $j\in p_{0}^{-1}(\{1\})$ such that $r\Vdash $ “ $\dot {g}\left ( n\right ) =j$ .” Since j is forced to be in $\dot {g}[R],$ it follows that $j\in A_{R}\cup s.$ Since j is also in $p_{0}^{-1}(\{1\}),$ we get that $j\in u.$ However, by the Claim 97, we get that $p\Vdash $ “ $n\in \dot {g}^{-1}\left ( u\right ) \subseteq B$ ,” which implies that $n\in B.$ This is a contradiction since $n\in R\setminus B.$ This finishes the proof.

We can now prove the following:

Theorem 98. Let V be a model of CH and $\kappa>\omega _{1}$ a regular cardinal. $\mathbb {C}_{\kappa }$ forces that there are no Katětov uniform MAD families of size $\omega _{1}.$

Proof Let $G\subseteq \mathbb {C}_{\kappa }$ be a generic filter. Assume there is $\mathcal {A}\in V\left [ G\right ] $ a Katětov uniform MAD family of size $\omega _{1}.$ Note that $\mathcal {A}$ most appear in an intermediate extension, so $\mathcal {A}$ is $\mathbb {C}$ -indestructible. By Proposition 19, we know that $\mathcal {A}$ has a tight restriction, but since $\mathcal {A}$ is uniform, it follows by Lemma 15 that $\mathcal {A}$ is already tight.

Let $X\in \left [ \kappa \right ] ^{\omega _{1}}$ such that $\mathcal {A}\in V\left [ G_{X}\right ] $ (where $G$ is the restriction of G to $\mathbb {C}_{X}$ ). We know that $V\left [ G\right ] =V\left [ G_{X}\right ] \left [ G_{\kappa \setminus X}\right ] .$ Let $C_{gen}$ be the first Cohen real added by $\mathbb {C}_{\kappa \setminus X}.$ By the Proposition 94, we get that (in $V\left [ G\right ] $ ) $\mathcal {A}\upharpoonright C_{gen} \nleq _{\textsf {SK}}$ $\mathcal {A}.$ It follows by Point 5 of Lemma 21 that $\mathcal {A}\upharpoonright C_{gen} \nleq _{\textsf {K}}\mathcal {A}.$

It is known that in the Cohen model, a MAD family is $\mathbb {C} $ -indestructible if and only if it has size $\omega _{1}.$ With the theorem above, it follows that if there are Katětov maximal MAD families in the Cohen model, then all of them are $\mathbb {C}$ -destructible. However, we do not know if there is such family. We conjecture that there are no Katětov maximal MAD families in such model, and we hope Theorem 98 is the first step of the proof.

Conjecture 99. There are no Katětov maximal MAD families in the Cohen model.

Nevertheless, by Theorem 13, there are weakly tight MAD families of size continuum in the Cohen model. So we could not rule out the possibility that a Katětov uniform, weakly tight MAD family exists in there.

8 Open questions

In this last section, we restate some of the main open problems regarding the Katětov order on MAD families, and add some new ones. The most important problems are the following:

Problem 100 [Reference Hrušák and Ferreira40].

Is it consistent that there is a Katětov-top MAD family?

Problem 101 [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1].

Is it consistent that there are no Katětov maximal MAD families?

The only way we know how to construct Katětov maximal MAD families is by constructing a Katětov uniform, weakly tight MAD family. So the following problem is natural:

Problem 102 [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1].

Is it consistent that there is a Katětov maximal MAD family that is not weakly tight?

We show that Katětov maximality does not imply tightness, but a completely different idea for weak tightness would be needed.

The results in Section 4 suggest the following:

Problem 103. Does the existence of a completely separable, weakly tight MAD family imply that there is no Katětov-top MAD family?

Regarding the generic existence of uniform MAD families, we ask:

Problem 104. Does the generic existence of uniform MAD families imply non $\left ( \mathcal {M}\right ) =\mathfrak {a=c}$ ?

The results in Section 6 suggest the following:

Problem 105. Is the statement “For every MAD family $\mathcal {A},$ there is a Sacks indestructible MAD family $\mathcal {B}$ such that $\mathcal {A}\leq _{\textsf {K}}\mathcal {B} $ ” consistent? What about for Cohen indestructibility?

We know there are no small Katětov maximal MAD family in the Cohen model, but we do not know if there are any of them.

Problem 106. Is there a Katětov maximal MAD family in the Cohen model? What about Katětov uniform MAD families?

We also do not know anything about the following:

Problem 107. What can be said about the statement: “For every MAD family $\mathcal {A},$ there is a Katětov maximal MAD family $\mathcal {B}$ such that $\mathcal {A}\leq _{\textsf {K}}\mathcal {B} $ ”?

All known constructions of Katětov maximal MAD family yield a MAD family of size $\mathfrak {c.}$ This led Hrušák to ask the following:

Problem 108 [Reference Hrušák37].

Is it consistent that there is a Katětov maximal MAD family of size less than $\mathfrak {c}$ ?

In the past, the author claimed to answer positively the previous problem. Unfortunately, the proof had a mistake. We want to take the opportunity to clarify that the problem remains open.

Acknowledgement

This paper would not have been possible without the valuable teachings from Michael Hrušák. I would like to thank him for being my guide and mentor in this MAD journey.

Funding

The research of the author was supported by a PAPIIT grant IA102222.

Footnotes

1 Unfamiliar concepts used in this introduction will be defined in the next section.

2 There are other notions of MAD families that could be considered as “analogues” of Ramsey ultrafilters. Some of them will be explored in a forthcoming paper with Brendle, Hrušák, and Raghavan.

3 If $\kappa $ is a cardinal, by H $\left ( \kappa \right ) $ we denote the collection of all sets with hereditary size less than $\kappa .$ For more information, the reader may consult [Reference Kunen50].

4 It might be the case that $w\left [ Y\right ] $ is finite for some $w\in \mathbb {W}\left ( S\right ) .$ This is why we did not wrote the conclusion of the proposition as “ $\{w\left [ Y\right ] \mid w\in \mathbb {W}\left ( S\right ) \}$ is an AD family” (but we could have said instead that $\{w\left [ Y\right ] \mid w\in \mathbb {W}\left ( S\right ) \}\setminus \left [ \omega \right ] ^{<\omega }$ is an AD family).

5 See [Reference Brendle and Yatabe9, Reference Hrušák and Zapletal44] for more results of this type.

References

Arciga-Alejandre, M., Hrušák, M., and Martinez-Ranero, C., Invariance properties of almost disjoint families, this Journal, vol. 78 (2013), no. 3, pp. 989–999.Google Scholar

Balcar, B. and Simon, P., Disjoint refinement , Handbook of Boolean Algebras, vol. 2 (J. D. Monk and R. Bonnet, editors), North-Holland, Amsterdam, 1989, pp. 333–388.Google Scholar

Bartoszyński, T. and Judah, H., Set Theory: On the Structure of the Real Line , A. K. Peters, Wellesley, MA, 1995.CrossRef Google Scholar

Blass, A., Combinatorial cardinal characteristics of the continuum , Handbook of Set Theory, vol. 1 (M. Foreman and A. Kanamori, editors), Springer, Dordrecht, 2010, pp. 395–489.CrossRef Google Scholar

Brendle, J., Mob families and mad families . Archive for Mathematical Logic , vol. 37 (1997), no. 3, pp. 183–197.CrossRef Google Scholar

Brendle, J. and Flašková, J., Generic existence of ultrafilters on the natural numbers . Fundamenta Mathematicae , vol. 236 (2017), no. 3, pp. 201–245.CrossRef Google Scholar

Brendle, J. and Hrušák, M., Countable Fréchet Boolean groups: An independence result, this Journal, vol. 74 (2009), no. 3, pp. 1061–1068.Google Scholar

Brendle, J. and Raghavan, D., Bounding, splitting, and almost disjointness . Annals of Pure and Applied Logic , vol. 165 (2014), no. 2, pp. 631–651.CrossRef Google Scholar

Brendle, J. and Yatabe, S., Forcing indestructibility of MAD families . Annals of Pure and Applied Logic , vol. 132 (2005), nos. 2–3, pp. 271–312.CrossRef Google Scholar

Brendle, J., Spinas, O., and Zhang, Y., Uniformity of the meager ideal and maximal cofinitary groups . Journal of Algebra , vol. 232 (2000), no. 1, pp. 209–225.CrossRef Google Scholar

Cancino-Manríquez, J., Every maximal ideal may be Katětov above of all

${F}_{\sigma }$ ideals . Transactions of the American Mathematical Society , vol. 375 (2022), no. 3, pp. 1861–1881.CrossRef Google Scholar

Cancino-Manríquez, J., I-ultrafilters in the rational perfect set model, this Journal (2022), online ahead of print, https://doi.org/10.1017/jsl.2022.81.CrossRef Google Scholar

Canjar, R. M., On the generic existence of special ultrafilters . Proceedings of the American Mathematical Society , vol. 110 (1990), no. 1, pp. 223–241.CrossRef Google Scholar

Chodounský, D. and Guzmán, O., Indestructibility of ideals and MAD families . Annals of Pure and Applied Logic , vol. 172 (2021), no. 5, Paper no. 102905, 20 pages.CrossRef Google Scholar

Chodounský, D., González, O. G., and Hrušák, M., Mathias–Prikry and Laver type forcing; summable ideals, coideals, and +-selective filters . Archive for Mathematical Logic , vol. 55 (2016), nos. 3-4, pp. 493–504.CrossRef Google Scholar

Corral, C. and Hrušák, M., Fréchet-like properties and almost disjoint families . Topology and its Applications , vol. 277 (2020), Article no. 107216, 11 pages.CrossRef Google Scholar

Dow, A., Two classes of Fréchet–Urysohn spaces . Proceedings of the American Mathematical Society , vol. 108 (1990), no. 1, pp. 241–247.Google Scholar

Dow, A., On MAD families and sequential order , Papers on General Topology and Applications (Amsterdam, 1994) (E. Coplakova and K. P. Hart, editors), Annals of the New York Academy of Sciences, vol. 788, New York Academy of Sciences, New York, 1996, pp. 79–94.Google Scholar

Enderton, H. B., Elements of Set Theory , Academic Press, New York, 1977.Google Scholar

Erdős, P. and Shelah, S., Separability properties of almost-disjoint families of sets . Israel Journal of Mathematics , vol. 12 (1972), pp. 207–214.CrossRef Google Scholar

Farah, I., Analytic quotients: Theory of liftings for quotients over analytic ideals on the integers . Memoirs of the American Mathematical Society , vol. 148 (2000), no. 702, pp. xvi+177.CrossRef Google Scholar

Fischer, V. and Törnquist, A., Template iterations and maximal cofinitary groups . Fundamenta Mathematicae , vol. 230 (2015), no. 3, pp. 205–236.CrossRef Google Scholar

Fischer, V., Schrittesser, D., and Törnquist, A., A co-analytic Cohen-indestructible maximal cofinitary group, this Journal, vol. 82 (2017), no. 2, pp. 629–647.Google Scholar

Flašková, J., Ideals and sequentially compact spaces . Topology Proceedings , vol. 33 (2009), pp. 107–121.Google Scholar

Flašková, J., I-ultrafilters and summable ideals , 10th Asian Logic Conference (T. Arai, J. Brendle, H. Kikyo, C. T. Chong, R. Downey, Q. Feng, and H. Ono, editors), World Scientific, Hackensack, NJ, 2010, pp. 113–123.Google Scholar

Gao, S. and Zhang, Y., Definable sets of generators in maximal cofinitary groups . Advances in Mathematics , vol. 217 (2008), no. 2, pp. 814–832.CrossRef Google Scholar

Goldbring, I., Ultrafilters Throughout Mathematics , Graduate Studies in Mathematics, vol. 220, American Mathematical Society, Providence, RI, 2022.CrossRef Google Scholar

Guzmán, O., On completely separable MAD families , Proceedings of the 2020 RIMS Meeting on Set Theory: Reals and Topology , 2020, to appear.Google Scholar

Guzmán, O. and Hrušák, M., On Pospíšil ideals . Topology and its Applications , vol. 259 (2019), pp. 242–250.CrossRef Google Scholar

Guzmán, O. and Kalajdzievski, D., The ultrafilter and almost disjointness numbers . Advances in Mathematics , vol. 386 (2021), 107805.CrossRef Google Scholar

Guzmán, O., Hrušák, M., and Martínez-Celis, A., Canjar filters II , Proceedings of the 2014 RIMS Meeting on Reflection Principles and Set Theory of Large Cardinals , Kyoto, Japan, 2014, pp. 59–67.Google Scholar

Guzmán, O., Hrušák, M., Martínez, C., and Ramos, A., Generic existence of mad families, this Journal, vol. 82 (2017), no. 1, pp. 303–316.Google Scholar

Guzmán-González, O. and Meza-Alcántara, D., Some structural aspects of the Katětov order on Borel ideals . Order , vol. 33 (2016), no. 2, pp. 189–194.CrossRef Google Scholar

Halbeisen, L. J., Combinatorial Set Theory , second ed., Springer Monographs in Mathematics, Springer, Cham, 2017. With a gentle introduction to forcing.CrossRef Google Scholar

Hernández-Hernández, F. and Hrušák, M., Cardinal invariants of analytic

$P$ -ideals . Canadian Journal of Mathematics , vol. 59 (2007), no. 3, pp. 575–595.CrossRef Google Scholar

Hrušák, M., MAD families and the rationals . Commentationes Mathematicae Universitatis Carolinae , vol. 42 (2001), no. 2, pp. 345–352.Google Scholar

Hrušák, M., Combinatorics of filters and ideals , Set Theory and its Applications (L. Babinkostova, A. E. Caicedo, S. Geschke, and M. Scheepers, editors), Contemporary Mathematics, vol. 533, American Mathematical Society, Providence, RI, 2011, pp. 29–69.CrossRef Google Scholar

Hrušák, M., Almost disjoint families and topology, Recent Progress in General Topology III (K. P. Hart, J. van Mill, and P. Simon, editors), Atlantis Press, Paris, 2014.Google Scholar

Hrušák, M., Katětov order on Borel ideals . Archive for Mathematical Logic , vol. 56 (2017), no. 7, pp. 831–847.CrossRef Google Scholar

Hrušák, M. and Ferreira, S. G., Ordering MAD families a la Katětov, this Journal, vol. 68 (2003), no. 4, pp. 1337–1353.Google Scholar

Hrušák, M. and Minami, H., Mathias–Prikry and Laver–Prikry type forcing . Annals of Pure and Applied Logic , vol. 165 (2014), no. 3, pp. 880–894.CrossRef Google Scholar

Hrušák, M. and Ramos-García, U. A., Malykhin’s problem . Advances in Mathematics , vol. 262 (2014), pp. 193–212.CrossRef Google Scholar

Hrušák, M. and Simon, P., Completely separable mad families , Open Problems in Topology II (Pearl, E., editor), Elsevier, Amsterdam, 2007, Chap. 19, pp. 179 – 184.CrossRef Google Scholar

Hrušák, M. and Zapletal, J., Forcing with quotients . Archive for Mathematical Logic , vol. 47 (2008), nos. 7–8, pp. 719–739.CrossRef Google Scholar

Hrušák, M., Steprans, J., and Zhang, Y., Cofinitary groups, almost disjoint and dominating families, this Journal, vol. 66 (2001), no. 3, pp. 1259–1276.Google Scholar

Jech, T., Set Theory , third millennium edition, revised and expanded, Springer Monographs in Mathematics, Springer, Berlin, 2003.Google Scholar

Kastermans, B., The complexity of maximal cofinitary groups . Proceedings of the American Mathematical Society , vol. 137 (2009), no. 1, pp. 307–316.CrossRef Google Scholar

Kastermans, B., Isomorphism types of maximal cofinitary groups . Bulletin of Symbolic Logic , vol. 15 (2009), no. 3, pp. 300–319.CrossRef Google Scholar

Katětov, M., Products of filters . Commentationes Mathematicae Universitatis Carolinae , vol. 9 (1968), pp. 173–189.Google Scholar

Kunen, K., Set Theory , Studies in Logic (London), vol. 34, College Publications, London, 2011.Google Scholar

Kurilić, M. S., Cohen-stable families of subsets of integers, this Journal, vol. 66 (2001), no. 1, pp. 257–270.Google Scholar

Laflamme, C., Zapping small filters . Proceedings of the American Mathematical Society , vol. 114 (1992), no. 2, pp. 535–544.CrossRef Google Scholar

Malliaris, M. and Shelah, S., Cofinality spectrum theorems in model theory, set theory, and general topology . Journal of the American Mathematical Society , vol. 29 (2016), no. 1, pp. 237–297.CrossRef Google Scholar

Mathias, A. R. D., Happy families . Annals of Mathematical Logic , vol. 12 (1977), no. 1, pp. 59–111.CrossRef Google Scholar

Michael, H., Meza-Alcántara, D., Thümmel, E., and Uzcátegui, C., Ramsey type properties of ideals . Annals of Pure and Applied Logic , vol. 168 (2017), no. 11, pp. 2022–2049.Google Scholar

Mildenberger, H., Raghavan, D., and Steprans, J., Splitting families and complete separability . Canadian Mathematical Bulletin , vol. 57 (2014), no. 1, pp. 119–124.CrossRef Google Scholar

Minami, H. and Sakai, H., Katětov and Katětov-Blass orders on

${F}_{\sigma }$ -ideals . Archive for Mathematical Logic , vol. 55 (2016), nos. 7–8, pp. 883–898.CrossRef Google Scholar

Moore, J. T., Hrušák, M., and Džamonja, M., Parametrized

$\diamondsuit$ principles . Transactions of the American Mathematical Society , vol. 356 (2004), no. 6, pp. 2281–2306.CrossRef Google Scholar

Raghavan, D. and Steprāns, J., On weakly tight families . Canadian Journal of Mathematics , vol. 64 (2012), no. 6, pp. 1378–1394.CrossRef Google Scholar

Shelah, S., Proper and Improper Forcing , second ed., Perspectives in Mathematical Logic, Springer, Berlin, 1998.CrossRef Google Scholar

Shelah, S., MAD saturated families and SANE player . Canadian Journal of Mathematics , vol. 63 (2011), no. 6, pp. 1416–1435.CrossRef Google Scholar

Zapletal, J., Forcing Idealized , Cambridge Tracts in Mathematics, vol. 174, Cambridge University Press, Cambridge, 2008.CrossRef Google Scholar

Article contents

KATĚTOV ORDER ON MAD FAMILIES

Abstract

Keywords

MSC classification

1 Introduction

Theorem 5 (Arciga, Hrušák, and Martínez [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1]).

Theorem 7 (García-Ferreira and Hrušák [Reference Hrušák and Ferreira40]).

2 Notation

3 Preliminaries

Theorem 13 (Mildenberger, Raghavan, and Steprāns [Reference Mildenberger, Raghavan and Steprans56] and [Reference Raghavan and Steprāns59]).

Proposition 14 (Hrušák [Reference Hrušák36], Kurilic [Reference Kurilić51]).

Lemma 17 [Reference Hrušák and Ferreira40].

Proposition 18 [Reference Brendle and Yatabe9, Reference Hrušák and Zapletal44].

Proposition 19 [Reference Hrušák and Ferreira40, Reference Kurilić51].

4 Katětov-top MAD families vs. $\mathfrak {s\leq b}$

Theorem 25 (Mathias [Reference Mathias54]).

5 A Katětov maximal MAD family from $\mathfrak {b=c}$

Proposition 30 [Reference Hrušák and Ferreira40].

Theorem 39 [Reference Brendle and Yatabe10].

Proposition 43 [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1].

6 Two more constructions

Theorem 60 [Reference Brendle, Spinas and Zhang9].

Proposition 67 ( $\mathfrak {h=c}$ ).

Proposition 79 ( $\mathfrak {h=c}$ ).

Problem 89 (Arciga, Hrušák, and Martínez).

Proposition 92 ( $\mathfrak {h=c}$ ).

7 The Cohen model

8 Open questions

Problem 100 [Reference Hrušák and Ferreira40].

Problem 101 [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1].

Problem 102 [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1].

Problem 108 [Reference Hrušák37].

Acknowledgement

Funding

Footnotes

References

Save article to Kindle

Save article to Dropbox

Save article to Google Drive

Reply to: Submit a response

Your details

You have entered the maximum number of contributors

Conflicting interests