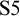1 Introduction
The possible world structures of Kripke [Reference Kripke32, Reference Kripke33] provide a very useful model theory for modal logics. Many propositional modal logics which arise naturally in alethic, temporal, epistemic, and deontic contexts can be shown to be sound and complete with respect to a class of relational (Kripke) frames. In many cases, this extends to multimodal logics, which include several modal operators, each of which is interpreted using its own accessibility relation on the set of worlds (points) of the frame. (The notions mentioned informally in this introductory section will be defined properly in Section 2.) While propositional logics allow the expression of many general intensional principles, these principles are in a sense all universal conditions. For example, it is possible to postulate axiomatically that generally,
![]() $\Box p$
only if p. Depending on the interpretation, this principle might say, e.g., that what is necessary is true, or that what is known is true. But it is impossible to postulate that this implication cannot be reversed, i.e., that there are cases in which p is true without
$\Box p$
only if p. Depending on the interpretation, this principle might say, e.g., that what is necessary is true, or that what is known is true. But it is impossible to postulate that this implication cannot be reversed, i.e., that there are cases in which p is true without
![]() $\Box p$
being true. Yet, it is equally natural to postulate that not every truth is known or necessary.
$\Box p$
being true. Yet, it is equally natural to postulate that not every truth is known or necessary.
A simple extension of a given propositional modal language allows for a straightforward regimentation of the example just given. This is the extension by quantifiers
![]() $\forall $
and
$\forall $
and
![]() $\exists $
binding the atomic proposition letters
$\exists $
binding the atomic proposition letters
![]() $p,q,r,\dots $
, which may then be conceived of as propositional variables. With these quantifiers, the relevant claim can be formulated as
$p,q,r,\dots $
, which may then be conceived of as propositional variables. With these quantifiers, the relevant claim can be formulated as
![]() $\exists p(p\wedge \neg \Box p)$
. Such extensions of modal logic were already considered in the earliest works on symbolic modal logic, by Lewis and Langford [Reference Lewis and Langford36], and their versatility in philosophical applications is evidenced in the work of Prior [Reference Prior43–Reference Prior47]. Propositional quantifiers are also straightforward to interpret on relational frames: when interpreting propositional formulas on such frames, each proposition letter is assigned a set of worlds—the set of worlds in which it is true. Thinking of propositional quantifiers as ranging over all possible interpretations of the variable which they bind, they are therefore straightforwardly interpreted as ranging over all sets of worlds. Such an interpretation of propositional quantifiers was already proposed by Kripke [Reference Kripke32].
$\exists p(p\wedge \neg \Box p)$
. Such extensions of modal logic were already considered in the earliest works on symbolic modal logic, by Lewis and Langford [Reference Lewis and Langford36], and their versatility in philosophical applications is evidenced in the work of Prior [Reference Prior43–Reference Prior47]. Propositional quantifiers are also straightforward to interpret on relational frames: when interpreting propositional formulas on such frames, each proposition letter is assigned a set of worlds—the set of worlds in which it is true. Thinking of propositional quantifiers as ranging over all possible interpretations of the variable which they bind, they are therefore straightforwardly interpreted as ranging over all sets of worlds. Such an interpretation of propositional quantifiers was already proposed by Kripke [Reference Kripke32].
It is natural to ask whether well-known completeness results of propositional modal logics with respect to classes of relational frames are preserved under the addition of propositional quantifiers. Many important results on this question were established around 1970, in particular by Bull [Reference Bull7], Kaplan [Reference Kaplan27], and Fine [Reference Fine12]. To state their results, let
![]() $\Lambda \pi +$
, for any normal modal logic
$\Lambda \pi +$
, for any normal modal logic
![]() $\Lambda $
, be the propositionally quantified modal logic of
$\Lambda $
, be the propositionally quantified modal logic of
![]() $\Lambda $
-frames, i.e., the set of formulas in the propositionally quantified modal language which are valid on the class of frames on which every theorem of
$\Lambda $
-frames, i.e., the set of formulas in the propositionally quantified modal language which are valid on the class of frames on which every theorem of
![]() $\Lambda $
is valid. The results of Bull, Kaplan, and Fine show that
$\Lambda $
is valid. The results of Bull, Kaplan, and Fine show that
![]() $\mathrm {S5}\pi +$
is axiomatizable; indeed, they show that
$\mathrm {S5}\pi +$
is axiomatizable; indeed, they show that
![]() $\mathrm {S5}\pi +$
is decidable, and provide a natural and independent axiomatization. Fine shows that this cannot be extended to a number of common modal logics which are weaker than
$\mathrm {S5}\pi +$
is decidable, and provide a natural and independent axiomatization. Fine shows that this cannot be extended to a number of common modal logics which are weaker than
![]() $\mathrm {S5}$
, as
$\mathrm {S5}$
, as
![]() $\mathrm {K}\pi +$
,
$\mathrm {K}\pi +$
,
![]() $\mathrm {T}\pi +$
,
$\mathrm {T}\pi +$
,
![]() $\mathrm {K4}\pi +$
,
$\mathrm {K4}\pi +$
,
![]() $\mathrm {S4}\pi +$
,
$\mathrm {S4}\pi +$
,
![]() $\mathrm {S4.2}\pi +$
, and
$\mathrm {S4.2}\pi +$
, and
![]() $\mathrm {B}\pi +$
are all not axiomatizable.
$\mathrm {B}\pi +$
are all not axiomatizable.
A few further results on the axiomatizability of propositionally quantified modal logics interpreted over relational frames have been obtained since then. Kremer [Reference Kremer30] notes that Fine’s unaxiomatizability results can be strengthened to show that the relevant logics are not just not axiomatizable, but in fact recursively isomorphic to second-order logic (understood as the validities of a second-order predicate language on standard models). A proof of this result for
![]() $\mathrm {S4.2}$
was presented by Kaminski and Tiomkin [Reference Kaminski and Tiomkin26], which extends to any modal logic
$\mathrm {S4.2}$
was presented by Kaminski and Tiomkin [Reference Kaminski and Tiomkin26], which extends to any modal logic
![]() $\Lambda $
weaker than
$\Lambda $
weaker than
![]() $\mathrm {S4.2}$
. More recently, Ding [Reference Ding10] has extended the decidability result from the class of frames validating
$\mathrm {S4.2}$
. More recently, Ding [Reference Ding10] has extended the decidability result from the class of frames validating
![]() $\mathrm {S5}$
to those validating
$\mathrm {S5}$
to those validating
![]() $\mathrm {KD4E}$
(aka
$\mathrm {KD4E}$
(aka
![]() $\mathrm {KD45}$
). Multimodal logics have been considered as well: Antonelli and Thomason [Reference Aldo Antonelli and Thomason1], Kuhn [Reference Kuhn34], and Belardinelli et al. [Reference Belardinelli, van der Hoek and Kuijer2] all show that the propositionally quantified bimodal logic on relational frames in which both modalities obey the principles of
$\mathrm {KD45}$
). Multimodal logics have been considered as well: Antonelli and Thomason [Reference Aldo Antonelli and Thomason1], Kuhn [Reference Kuhn34], and Belardinelli et al. [Reference Belardinelli, van der Hoek and Kuijer2] all show that the propositionally quantified bimodal logic on relational frames in which both modalities obey the principles of
![]() $\mathrm {S5}$
is recursively isomorphic to second-order logic, and Fritz [Reference Fritz16] extends this to the corresponding class of product frames, which validate certain interaction principles between the two modalities.
$\mathrm {S5}$
is recursively isomorphic to second-order logic, and Fritz [Reference Fritz16] extends this to the corresponding class of product frames, which validate certain interaction principles between the two modalities.
While these existing axiomatizability results cover many of the most well-known modal logics, the findings are at present somewhat unsystematic. This paper aims to improve this situation, by developing general methods by which a more complete picture can be obtained. First, as Ding [Reference Ding10, p. 1148] notes, it appears from the known results as if there is an “axiomatizability boundary” which divides normal modal logics according to strength, with a normal modal logic
![]() $\Lambda $
being above the boundary if and only if
$\Lambda $
being above the boundary if and only if
![]() $\Lambda \pi +$
is axiomatizable. We show that such a boundary does indeed exist among a wide class of normal modal logics, as in these cases, the complexity of
$\Lambda \pi +$
is axiomatizable. We show that such a boundary does indeed exist among a wide class of normal modal logics, as in these cases, the complexity of
![]() $\Lambda \pi +$
decreases monotonically with the strength of
$\Lambda \pi +$
decreases monotonically with the strength of
![]() $\Lambda $
. We note that the result does not extend to all normal modal logics.
$\Lambda $
. We note that the result does not extend to all normal modal logics.
The current understanding is especially limited when it comes to axiomatizable logics: only two non-trivial normal modal logics—
![]() $\mathrm {KD4E}$
and
$\mathrm {KD4E}$
and
![]() $\mathrm {S5}$
—have been identified as defining classes of frames whose propositionally quantified modal logics are axiomatizable (indeed, decidable). We will develop a new technique for showing the decidability of
$\mathrm {S5}$
—have been identified as defining classes of frames whose propositionally quantified modal logics are axiomatizable (indeed, decidable). We will develop a new technique for showing the decidability of
![]() $\Lambda \pi +$
which can be applied to many more strong normal modal logics
$\Lambda \pi +$
which can be applied to many more strong normal modal logics
![]() $\Lambda $
. Most notably, this includes
$\Lambda $
. Most notably, this includes
![]() $\mathrm {KE}$
and every one of its normal modal extension. We also simplify the construction presented in Kaminski and Tiomkin [Reference Kaminski and Tiomkin26] which makes it applicable to a wider range of normal modal logics. With these two general methods, we are able to trace the axiomatizability boundary in fine detail both from above and from below. Figure 1 summarizes many of the central results: It presents a number of normal modal logics, ordered according to strength (inclusion). The figure indicates the axiomatizability boundary using a dotted line: for any logic
$\mathrm {KE}$
and every one of its normal modal extension. We also simplify the construction presented in Kaminski and Tiomkin [Reference Kaminski and Tiomkin26] which makes it applicable to a wider range of normal modal logics. With these two general methods, we are able to trace the axiomatizability boundary in fine detail both from above and from below. Figure 1 summarizes many of the central results: It presents a number of normal modal logics, ordered according to strength (inclusion). The figure indicates the axiomatizability boundary using a dotted line: for any logic
![]() $\Lambda $
included in the diagram above this line,
$\Lambda $
included in the diagram above this line,
![]() $\Lambda \pi +$
is axiomatizable (indeed, decidable), and for any logic
$\Lambda \pi +$
is axiomatizable (indeed, decidable), and for any logic
![]() $\Lambda $
included in the diagram below this line,
$\Lambda $
included in the diagram below this line,
![]() $\Lambda \pi +$
is not axiomatizable (and in most cases recursively isomorphic to second-order logic). The various modal logics included in Figure 1 will be defined below; see Figure 2. For reasons of uniformity, we follow the notational conventions for modal axioms and logics of Hughes and Cresswell [Reference Hughes and Cresswell25, pp. 359–368] throughout, from which the arrangement of logics in Figure 1 is adapted as well. (The definition of
$\Lambda \pi +$
is not axiomatizable (and in most cases recursively isomorphic to second-order logic). The various modal logics included in Figure 1 will be defined below; see Figure 2. For reasons of uniformity, we follow the notational conventions for modal axioms and logics of Hughes and Cresswell [Reference Hughes and Cresswell25, pp. 359–368] throughout, from which the arrangement of logics in Figure 1 is adapted as well. (The definition of
![]() $\mathrm {K3}$
is missing from Hughes and Cresswell [Reference Hughes and Cresswell25], but it can be found in Hughes and Cresswell [Reference Hughes and Cresswell23, Appendix 3]. We have also changed some inclusion relations from the diagram of Hughes and Cresswell [Reference Hughes and Cresswell25] to correct what appear to be oversights.)
$\mathrm {K3}$
is missing from Hughes and Cresswell [Reference Hughes and Cresswell25], but it can be found in Hughes and Cresswell [Reference Hughes and Cresswell23, Appendix 3]. We have also changed some inclusion relations from the diagram of Hughes and Cresswell [Reference Hughes and Cresswell25] to correct what appear to be oversights.)

Figure 1 The axiomatizability boundary (dotted) among some finitely axiomatized normal modal logics.

Figure 2 Propositional unimodal axioms and logics.
Figure 1 only summarizes the results of this paper for a selection of unimodal logics discussed in the literature. The techniques developed and improved here are applicable more widely, and we establish results which are in several ways stronger than what is conveyed in the figure. For example, in many cases, establishing the unaxiomatizability of a given logic extends to all of its weakenings, and in some cases establishing the axiomatizability of a given logic extends to all of its strengthenings. The techniques used to establish these results are also applicable to multimodal logics. This is especially interesting in the case of the decidability results, as there are at present no decidability results for propositionally quantified multimodal logics. As an example, we will show the decidability of the propositionally quantified modal logic of bimodal relational frames in which both accessibility relations are equivalence relations, one of which is a refinement of the other.
The paper is organized as follows: Section 2 defines the basic concepts of propositionally quantified modal logics and relational frames. Section 3 develops a new method for establishing the decidability of
![]() $\Lambda \pi +$
, and applies it to a range of unimodal examples. Section 4 presents the simplified construction for establishing that
$\Lambda \pi +$
, and applies it to a range of unimodal examples. Section 4 presents the simplified construction for establishing that
![]() $\Lambda \pi +$
is recursively isomorphic to second-order logic, and applies it to a range of unimodal examples. Section 5 considers the special case of extensions of
$\Lambda \pi +$
is recursively isomorphic to second-order logic, and applies it to a range of unimodal examples. Section 5 considers the special case of extensions of
![]() $\mathrm {K4.3}$
, which requires different methods. Section 6 considers multimodal logics. The final Section 7 concludes with some open problems.
$\mathrm {K4.3}$
, which requires different methods. Section 6 considers multimodal logics. The final Section 7 concludes with some open problems.
2 Basic concepts
This section sets up more rigorously the questions to be answered below and some common logical concepts to be used in developing the answers. We recall only briefly standard definitions of normal modal logics and relational frames; for fuller developments, see a standard textbook such as [Reference Hughes and Cresswell25]. For the required recursion-theoretic notions, see [Reference Blackburn, de Rijke and Venema4, Appendix C].
2.1 Normal modal logics and relational frames
We start with the syntax of the propositionally quantified languages. In order to accommodate multimodal system, we define the language relative to a finite or countably infinite set of operators O. The relativity to this set of operators will mostly be assumed tacitly.
Definition 2.1. For any finite or countably infinite set O,
![]() $\mathcal {L}^O$
is the language whose formulas are specified in Backus–Naur form (BNF) as follows:
$\mathcal {L}^O$
is the language whose formulas are specified in Backus–Naur form (BNF) as follows:
where p indicates any member of a countably infinite set of propositional variables
![]() $\Phi $
, and
$\Phi $
, and
![]() $\Box $
indicates any member of O.
$\Box $
indicates any member of O.
![]() $\mathcal {L}^O_{\mathrm {qf}}$
is the set of quantifier-free formulas of
$\mathcal {L}^O_{\mathrm {qf}}$
is the set of quantifier-free formulas of
![]() $\mathcal {L}^O$
.
$\mathcal {L}^O$
.
As usual, we treat other Boolean operators like
![]() $\neg $
,
$\neg $
,
![]() $\wedge $
,
$\wedge $
,
![]() $\vee $
,
$\vee $
,
![]() $\leftrightarrow $
, and
$\leftrightarrow $
, and
![]() $\top $
as syntactic abbreviations; e.g., we use
$\top $
as syntactic abbreviations; e.g., we use
![]() $\neg \varphi $
to abbreviate
$\neg \varphi $
to abbreviate
![]() $\varphi \to \bot $
, and
$\varphi \to \bot $
, and
![]() $\top $
to abbreviate
$\top $
to abbreviate
![]() $\neg \bot $
. Similarly,
$\neg \bot $
. Similarly,
![]() $\Diamond $
and
$\Diamond $
and
![]() $\exists p$
abbreviate the duals of
$\exists p$
abbreviate the duals of
![]() $\Box $
and
$\Box $
and
![]() $\forall p$
, respectively. We use
$\forall p$
, respectively. We use
![]() $\bigwedge $
and
$\bigwedge $
and
![]() $\bigvee $
for finite conjunctions and disjunctions, writing, e.g.,
$\bigvee $
for finite conjunctions and disjunctions, writing, e.g.,
![]() $\bigwedge _{i=1}^np_i$
for
$\bigwedge _{i=1}^np_i$
for
![]() $p_1\wedge \cdots \wedge p_n$
. We also introduce some less familiar abbreviations: For any formula
$p_1\wedge \cdots \wedge p_n$
. We also introduce some less familiar abbreviations: For any formula
![]() $\varphi $
,
$\varphi $
,
![]() $\bar {\forall }\varphi $
abbreviates
$\bar {\forall }\varphi $
abbreviates
![]() $\forall p_1\dots \forall p_n\varphi $
, where
$\forall p_1\dots \forall p_n\varphi $
, where
![]() $p_1,\dots ,p_n$
are the free variables in
$p_1,\dots ,p_n$
are the free variables in
![]() $\varphi $
. Further, if O is finite, then for any
$\varphi $
. Further, if O is finite, then for any
![]() $n\in \mathbb {N}$
and formula
$n\in \mathbb {N}$
and formula
![]() $\varphi $
, we define
$\varphi $
, we define
![]() $O^n\varphi $
and
$O^n\varphi $
and
![]() $O^{\leq n}\varphi $
using the following induction:
$O^{\leq n}\varphi $
using the following induction:
 $$ \begin{align*} \begin{array}{ll} O^0\varphi:=\varphi, & O^{\leq0}\varphi:=\varphi, \\ O^{n+1}\varphi:=\bigwedge_{\Box\in O}\Box O^n\varphi, & O^{\leq n+1}\varphi:=\varphi\wedge\bigwedge_{\Box\in O}\Box O^{\leq n}\varphi. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} O^0\varphi:=\varphi, & O^{\leq0}\varphi:=\varphi, \\ O^{n+1}\varphi:=\bigwedge_{\Box\in O}\Box O^n\varphi, & O^{\leq n+1}\varphi:=\varphi\wedge\bigwedge_{\Box\in O}\Box O^{\leq n}\varphi. \end{array} \end{align*} $$
We further shorten
![]() $\{\Box \}^n\varphi $
and
$\{\Box \}^n\varphi $
and
![]() $\{\Box \}^{\leq n}\varphi $
to
$\{\Box \}^{\leq n}\varphi $
to
![]() $\Box ^n\varphi $
and
$\Box ^n\varphi $
and
![]() $\Box ^{\leq n}\varphi $
, respectively.
$\Box ^{\leq n}\varphi $
, respectively.
Normal modal logics can be understood as sets of quantifier-free formulas containing certain axioms and closed under certain rules. In order to state one of these rules, let
![]() $\varphi [\psi /p]$
be the result of replacing every occurrence of the propositional variable p in the formula
$\varphi [\psi /p]$
be the result of replacing every occurrence of the propositional variable p in the formula
![]() $\varphi $
by the formula
$\varphi $
by the formula
![]() $\psi $
. In cases in which
$\psi $
. In cases in which
![]() $\varphi $
contains quantifiers, this is only defined if
$\varphi $
contains quantifiers, this is only defined if
![]() $\psi $
is free for p in
$\psi $
is free for p in
![]() $\varphi $
, i.e., if every free occurrence of every variable q in
$\varphi $
, i.e., if every free occurrence of every variable q in
![]() $\psi $
remains free in
$\psi $
remains free in
![]() $\varphi [\psi /p]$
.
$\varphi [\psi /p]$
.
Definition 2.2. A normal modal logic is a subset of
![]() $\mathcal {L}^O_{\mathrm {qf}}$
which, for every modality
$\mathcal {L}^O_{\mathrm {qf}}$
which, for every modality
![]() $\Box \in O$
, contains every classical tautology and the distributivity axiom
$\Box \in O$
, contains every classical tautology and the distributivity axiom
![]() $\mathrm {K}^{\Box }$
:
$\mathrm {K}^{\Box }$
:
![]() $\Box (p\to q)\to (\Box p\to \Box q)$
, and is closed under the rules of modus
$\Box (p\to q)\to (\Box p\to \Box q)$
, and is closed under the rules of modus
![]() $\mathrm {MP}$
:
$\mathrm {MP}$
:
![]() $\varphi ,\varphi \to \psi /\psi $
, necessitation
$\varphi ,\varphi \to \psi /\psi $
, necessitation
![]() $\mathrm {Nec}$
:
$\mathrm {Nec}$
:
![]() $\varphi /\Box \varphi $
, and uniform substitution
$\varphi /\Box \varphi $
, and uniform substitution
![]() $\mathrm {US}$
:
$\mathrm {US}$
:
![]() $\varphi /\varphi [\psi /p]$
.
$\varphi /\varphi [\psi /p]$
.
![]() $\mathrm {K}$
is the smallest normal modal logic. If
$\mathrm {K}$
is the smallest normal modal logic. If
![]() $\Lambda $
is a normal modal logic and
$\Lambda $
is a normal modal logic and
![]() $\Gamma \subseteq \mathcal {L}^O_{\mathrm {qf}}$
, then
$\Gamma \subseteq \mathcal {L}^O_{\mathrm {qf}}$
, then
![]() $\Lambda +\Gamma $
is the smallest normal modal logic including both
$\Lambda +\Gamma $
is the smallest normal modal logic including both
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Gamma $
. If
$\Gamma $
. If
![]() $\Gamma =\{\gamma _1,\dots ,\gamma _n\}$
, we also write this logic as
$\Gamma =\{\gamma _1,\dots ,\gamma _n\}$
, we also write this logic as
![]() $\Lambda +\gamma _1+\dots +\gamma _n$
.
$\Lambda +\gamma _1+\dots +\gamma _n$
.
This definition presupposes that there is always a unique smallest normal modal logic including a given set. This claim is easily seen to be witnessed by the intersection of all normal modal logics including the relevant set. Having defined the general notion of a normal modal logic, we can now define the various unimodal logics included in Figure 1. They will be discussed in more detail below, but for ease of reference, we present them all together in Figure 2. To forestall a likely source of confusion, note that whereas
![]() $\mathrm {K4}$
is the extension of
$\mathrm {K4}$
is the extension of
![]() $\mathrm {K}$
by the axiom
$\mathrm {K}$
by the axiom
![]() $\mathbf {4}$
, the names for
$\mathbf {4}$
, the names for
![]() $\mathrm {K1.1/2}$
,
$\mathrm {K1.1/2}$
,
![]() $\mathrm {K2(.1)}$
, and
$\mathrm {K2(.1)}$
, and
![]() $\mathrm {K3.1}$
, which go back to Sobociński [Reference Sobociński55], have no such origin. Instead, they appear to derive merely from an enumeration of certain extensions of
$\mathrm {K3.1}$
, which go back to Sobociński [Reference Sobociński55], have no such origin. Instead, they appear to derive merely from an enumeration of certain extensions of
![]() $\mathrm {S4M}$
, which Sobociński labels
$\mathrm {S4M}$
, which Sobociński labels
![]() $\mathrm {K1}$
.
$\mathrm {K1}$
.
We say that a normal modal logic is axiomatizable if it is a recursively enumerable set. In fact, we will call any set of formulas of any of the languages considered here axiomatizable just in case it is recursively enumerable.
Turning from the syntactic to the model-theoretic side, we define the well-known concept of a relational frame, and the evaluation of a formula relative to a world of the frame and an assignment function mapping each propositional variable to the set of worlds in which it is to be evaluated as true. The usual concept of a relational (Kripke) model can be understood as consisting of a relational frame and an assignment function. We make use of two items of notation to state the clauses for modal operators and quantifiers, respectively: First, we write
![]() $R[w]$
for the set of elements R-accessible from w, i.e.,
$R[w]$
for the set of elements R-accessible from w, i.e.,
![]() $\{v:wRv\}$
. For later uses, we also extend this notation to any set x, writing
$\{v:wRv\}$
. For later uses, we also extend this notation to any set x, writing
![]() $R[x]$
for
$R[x]$
for
![]() $\{v:wRv\:\&\:w\in x\}$
. Second, we write
$\{v:wRv\:\&\:w\in x\}$
. Second, we write
![]() $a[x/p]$
for the function mapping p to x and every other
$a[x/p]$
for the function mapping p to x and every other
![]() $q\in \Phi $
to
$q\in \Phi $
to
![]() $a(q)$
.
$a(q)$
.
Definition 2.3. A relational frame (for O) is a structure
![]() $\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
such that W is a set, and for every
$\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
such that W is a set, and for every
![]() $\Box \in O$
,
$\Box \in O$
,
![]() $R_{\Box }$
is a binary relation on W. For every
$R_{\Box }$
is a binary relation on W. For every
![]() $w\in W$
and assignment function
$w\in W$
and assignment function
![]() $a:\Phi \to \mathcal {P}(W)$
,
$a:\Phi \to \mathcal {P}(W)$
,
![]() $\varphi $
being true relative to w and a is recursively defined as follows:
$\varphi $
being true relative to w and a is recursively defined as follows:
-
 $\mathfrak {F},w,a\Vdash p$
iff
$\mathfrak {F},w,a\Vdash p$
iff
 $w\in a(p)$
;
$w\in a(p)$
; -
 $\mathfrak {F},w,a\nVdash \bot $
;
$\mathfrak {F},w,a\nVdash \bot $
; -
 $\mathfrak {F},w,a\Vdash \varphi \to \psi $
iff
$\mathfrak {F},w,a\Vdash \varphi \to \psi $
iff
 $\mathfrak {F},w,a\Vdash \varphi $
only if
$\mathfrak {F},w,a\Vdash \varphi $
only if
 $\mathfrak {F},w,a\Vdash \psi $
;
$\mathfrak {F},w,a\Vdash \psi $
; -
 $\mathfrak {F},w,a\Vdash \Box \varphi $
iff
$\mathfrak {F},w,a\Vdash \Box \varphi $
iff
 $\mathfrak {F},v,a\Vdash \varphi $
for all
$\mathfrak {F},v,a\Vdash \varphi $
for all
 $v\in R_{\Box }[w]$
;
$v\in R_{\Box }[w]$
; -
 $\mathfrak {F},w,a\Vdash \forall p\varphi $
iff
$\mathfrak {F},w,a\Vdash \forall p\varphi $
iff
 $\mathfrak {F},w,a[x/p]\Vdash \varphi $
for all
$\mathfrak {F},w,a[x/p]\Vdash \varphi $
for all
 $x\subseteq W$
;
$x\subseteq W$
;
![]() $\varphi $
is valid in w, written
$\varphi $
is valid in w, written
![]() $\mathfrak {F},w\Vdash \varphi $
, if
$\mathfrak {F},w\Vdash \varphi $
, if
![]() $\mathfrak {F},w,a\Vdash \varphi $
for every assignment function a.
$\mathfrak {F},w,a\Vdash \varphi $
for every assignment function a.
![]() $\varphi $
is valid in
$\varphi $
is valid in
![]() $\mathfrak {F}$
, written
$\mathfrak {F}$
, written
![]() $\mathfrak {F}\Vdash \varphi $
, if
$\mathfrak {F}\Vdash \varphi $
, if
![]() $\mathfrak {F},w\Vdash \varphi $
for every
$\mathfrak {F},w\Vdash \varphi $
for every
![]() $w\in W$
.
$w\in W$
.
![]() $\varphi $
is valid on a class of relational frames
$\varphi $
is valid on a class of relational frames
![]() $\mathsf {C}$
, written
$\mathsf {C}$
, written
![]() $\mathsf {C}\Vdash \varphi $
, if
$\mathsf {C}\Vdash \varphi $
, if
![]() $\mathfrak {F}\Vdash \varphi $
for every
$\mathfrak {F}\Vdash \varphi $
for every
![]() $\mathfrak {F}$
in
$\mathfrak {F}$
in
![]() $\mathsf {C}$
.
$\mathsf {C}$
.
In the unimodal case, we omit the index
![]() $\Box $
, and write
$\Box $
, and write
![]() $\langle W,R\rangle $
for a frame. The different notions of validity are extended to sets of formulas: a set of formulas is valid just in case all of its members are valid in the relevant sense. Satisfiability is dual to validity: a formula is satisfiable (in a world, in a frame, or on a class) if its negation is not valid (in the same sense). We consider the size of a frame
$\langle W,R\rangle $
for a frame. The different notions of validity are extended to sets of formulas: a set of formulas is valid just in case all of its members are valid in the relevant sense. Satisfiability is dual to validity: a formula is satisfiable (in a world, in a frame, or on a class) if its negation is not valid (in the same sense). We consider the size of a frame
![]() $\langle W,R_{\Box }\rangle _{\Box \in O}$
to be
$\langle W,R_{\Box }\rangle _{\Box \in O}$
to be
![]() $|W|$
, the cardinality of the set of worlds.
$|W|$
, the cardinality of the set of worlds.
The notion of being valid in a relational frame gives rise to two crucial notions connecting sets of formulas and classes of relational frames: for any set of formulas
![]() $\Gamma $
, there is the class of relational frames defined by
$\Gamma $
, there is the class of relational frames defined by
![]() $\Gamma $
, written
$\Gamma $
, written
![]() $\mathsf {R}(\Gamma )$
, and for any class of relational frames
$\mathsf {R}(\Gamma )$
, and for any class of relational frames
![]() $\mathsf {C}$
, there is the propositionally quantified modal logic of
$\mathsf {C}$
, there is the propositionally quantified modal logic of
![]() $\mathsf {C}$
, written
$\mathsf {C}$
, written
![]() $\mathcal {L}(\mathsf {C})$
. With this, the propositionally quantified extension
$\mathcal {L}(\mathsf {C})$
. With this, the propositionally quantified extension
![]() $\Lambda \pi +$
of a given normal modal logic
$\Lambda \pi +$
of a given normal modal logic
![]() $\Lambda $
can be defined:
$\Lambda $
can be defined:
Definition 2.4. Let
![]() $\Gamma \subseteq \mathcal {L}^O$
,
$\Gamma \subseteq \mathcal {L}^O$
,
![]() $\mathsf {C}$
a class of relational frames, and
$\mathsf {C}$
a class of relational frames, and
![]() $\Lambda $
a normal modal logic. Then:
$\Lambda $
a normal modal logic. Then:
-
 $\mathsf {R}(\Gamma )$
is the class of relational frames
$\mathsf {R}(\Gamma )$
is the class of relational frames
 $\mathfrak {F}$
such that
$\mathfrak {F}$
such that
 $\mathfrak {F}\Vdash \gamma $
for all
$\mathfrak {F}\Vdash \gamma $
for all
 $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
. -
 $\mathcal {L}(\mathsf {C}):=\{\varphi \in \mathcal {L}^O:\mathsf {C}\Vdash \varphi \}.$
$\mathcal {L}(\mathsf {C}):=\{\varphi \in \mathcal {L}^O:\mathsf {C}\Vdash \varphi \}.$
-
 $\Lambda \pi +:=\mathcal {L}(\mathsf {R}(\Lambda )).$
$\Lambda \pi +:=\mathcal {L}(\mathsf {R}(\Lambda )).$
The validities on any relational frame contain the axioms used in the definition of normal modal logics, and are closed under the rules used in this definition. Consequently, for any
![]() $\Gamma \subseteq \mathcal {L}^O_{\mathrm {qf}}$
,
$\Gamma \subseteq \mathcal {L}^O_{\mathrm {qf}}$
,
![]() $\mathsf {R}(\mathrm {K}\Gamma )$
is
$\mathsf {R}(\mathrm {K}\Gamma )$
is
![]() $\mathsf {R}(\Gamma )$
, and
$\mathsf {R}(\Gamma )$
, and
![]() $\mathcal {L}(\mathsf {R}(\Gamma ))$
is
$\mathcal {L}(\mathsf {R}(\Gamma ))$
is
![]() $\mathrm {K}\Gamma \pi +$
. It is also worth noting that
$\mathrm {K}\Gamma \pi +$
. It is also worth noting that
![]() $\Lambda \pi +$
is consistent just in case
$\Lambda \pi +$
is consistent just in case
![]() $\Lambda $
is consistent; this follows from Makinson’s [Reference Makinson38] result that every consistent normal modal logic is valid in some one-element frame.
$\Lambda $
is consistent; this follows from Makinson’s [Reference Makinson38] result that every consistent normal modal logic is valid in some one-element frame.
2.2 Generated subframes
The addition of propositional quantifiers preserves an important feature of modal languages interpreted on relational frames: the truth of a formula
![]() $\varphi $
in a world w is dependent only on the subframe consisting of those worlds which are accessible from w by a finite sequence of steps along the accessibility relations. More carefully, if
$\varphi $
in a world w is dependent only on the subframe consisting of those worlds which are accessible from w by a finite sequence of steps along the accessibility relations. More carefully, if
![]() $\varphi $
contains at most n nested modal operators, only those worlds accessible by n steps along the accessibility relations are relevant. This fact will be appealed to repeatedly in the following, so we introduce the necessary definitions and results, even though they are essentially unchanged from the familiar quantifier-free setting; compare Blackburn et al. [Reference Blackburn, de Rijke and Venema4, p. 140].
$\varphi $
contains at most n nested modal operators, only those worlds accessible by n steps along the accessibility relations are relevant. This fact will be appealed to repeatedly in the following, so we introduce the necessary definitions and results, even though they are essentially unchanged from the familiar quantifier-free setting; compare Blackburn et al. [Reference Blackburn, de Rijke and Venema4, p. 140].
First, we introduce the notion of the modal depth of a formula
![]() $\varphi $
as the maximal number of nested modal operators in
$\varphi $
as the maximal number of nested modal operators in
![]() $\varphi $
. Alongside this, we introduce the corresponding notion of quantifier depth for quantifiers.
$\varphi $
. Alongside this, we introduce the corresponding notion of quantifier depth for quantifiers.
Definition 2.5.
![]() $\mathrm {md}$
and
$\mathrm {md}$
and
![]() $\mathrm {qd}$
are the functions from
$\mathrm {qd}$
are the functions from
![]() $\mathcal {L}^O$
to
$\mathcal {L}^O$
to
![]() $\mathbb {N}$
defined using the recursive clauses specified by the following table:
$\mathbb {N}$
defined using the recursive clauses specified by the following table:

![]() $\mathrm {md}(\varphi )$
is the modal depth of
$\mathrm {md}(\varphi )$
is the modal depth of
![]() $\varphi $
;
$\varphi $
;
![]() $\mathrm {qd}(\varphi )$
is the quantifier depth of
$\mathrm {qd}(\varphi )$
is the quantifier depth of
![]() $\varphi $
.
$\varphi $
.
Next, we define the notion of an ((n-step) generated) subframe. To do so, we restrict any binary relation R to a set x by writing
![]() $R|x$
for
$R|x$
for
![]() $\{\langle w,v\rangle :wRv\:\&\:w,v\in x\}$
. Later on, we similarly write
$\{\langle w,v\rangle :wRv\:\&\:w,v\in x\}$
. Later on, we similarly write
![]() $f|x$
for the restriction of a function f to a subset x of its domain.
$f|x$
for the restriction of a function f to a subset x of its domain.
Definition 2.6. Let
![]() $\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
be a relational frame.
$\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
be a relational frame.
![]() $\mathfrak {F}'=\langle W',R^{\prime }_{\Box }\rangle ^{}_{\Box \in O}$
is a subframe of
$\mathfrak {F}'=\langle W',R^{\prime }_{\Box }\rangle ^{}_{\Box \in O}$
is a subframe of
![]() $\mathfrak {F}$
if
$\mathfrak {F}$
if
![]() $W'\subseteq W$
and
$W'\subseteq W$
and
![]() $R^{\prime }_{\Box }=R_{\Box }|W'$
for all
$R^{\prime }_{\Box }=R_{\Box }|W'$
for all
![]() $\Box \in O$
. For any
$\Box \in O$
. For any
![]() $x\subseteq W$
and
$x\subseteq W$
and
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
 $$ \begin{align*} \begin{array}{ll} W_x^0:=x, &\\ W_x^{n+1}:=W_x^n\cup\bigcup_{\Box\in O}R_{\Box}[W_x^n], & \mathfrak{F}_x^n:=\langle W_x^n,R_{\Box}|W_x^n\rangle_{\Box\in O}, \\ W_x:=\bigcup_{n\in\mathbb{N}}W_x^n, &\mathfrak{F}_x:=\langle W_x,R_{\Box}|W_x\rangle_{\Box\in O}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} W_x^0:=x, &\\ W_x^{n+1}:=W_x^n\cup\bigcup_{\Box\in O}R_{\Box}[W_x^n], & \mathfrak{F}_x^n:=\langle W_x^n,R_{\Box}|W_x^n\rangle_{\Box\in O}, \\ W_x:=\bigcup_{n\in\mathbb{N}}W_x^n, &\mathfrak{F}_x:=\langle W_x,R_{\Box}|W_x\rangle_{\Box\in O}. \end{array} \end{align*} $$
![]() $\mathfrak {F}_x^{(n)}$
is the (n-step) subframe of
$\mathfrak {F}_x^{(n)}$
is the (n-step) subframe of
![]() $\mathfrak {F}$
generated by x. If x is a singleton
$\mathfrak {F}$
generated by x. If x is a singleton
![]() $\{w\}$
, we call the subframes point-generated, and omit set brackets, writing
$\{w\}$
, we call the subframes point-generated, and omit set brackets, writing
![]() $\mathfrak {F}_w^{(n)}$
for
$\mathfrak {F}_w^{(n)}$
for
![]() $\mathfrak {F}_{\{w\}}^{(n)}$
.
$\mathfrak {F}_{\{w\}}^{(n)}$
.
We can now show that a formula
![]() $\varphi $
is valid in a world w of a frame just in case it is valid in w in a subframe generated by a set containing w, as well as in the corresponding n-step generated subframes, as long as n is at least as great as the modal depth of
$\varphi $
is valid in a world w of a frame just in case it is valid in w in a subframe generated by a set containing w, as well as in the corresponding n-step generated subframes, as long as n is at least as great as the modal depth of
![]() $\varphi $
.
$\varphi $
.
Proposition 2.7. Let
![]() $\mathfrak {F}$
be a relational frame, x a set of worlds,
$\mathfrak {F}$
be a relational frame, x a set of worlds,
![]() $w\in x$
,
$w\in x$
,
![]() $\varphi \in \mathcal {L}^O$
, and
$\varphi \in \mathcal {L}^O$
, and
![]() $n\geq \mathrm {md}(\varphi )$
. Then,
$n\geq \mathrm {md}(\varphi )$
. Then,
Proof Routine, by an induction on the complexity of
![]() $\varphi $
relative to corresponding assignment functions.
$\varphi $
relative to corresponding assignment functions.
2.3 The axiomatizability boundary
Using generated subframes, we can now establish the (partial) axiomatizability boundary mentioned above. The crucial observation is that among certain sets of formulas
![]() $\Gamma \subseteq \mathcal {L}^O$
, the complexity of
$\Gamma \subseteq \mathcal {L}^O$
, the complexity of
![]() $\mathcal {L}(\mathsf {R}(\Gamma ))$
decreases monotonically with the strength of
$\mathcal {L}(\mathsf {R}(\Gamma ))$
decreases monotonically with the strength of
![]() $\Gamma $
. That is, if
$\Gamma $
. That is, if
![]() $\Gamma \subseteq \Delta $
, then
$\Gamma \subseteq \Delta $
, then
![]() $\mathcal {L}(\mathsf {R}(\Delta ))$
is reducible to
$\mathcal {L}(\mathsf {R}(\Delta ))$
is reducible to
![]() $\mathcal {L}(\mathsf {R}(\Gamma ))$
in the sense that there is a computable function
$\mathcal {L}(\mathsf {R}(\Gamma ))$
in the sense that there is a computable function
![]() $f:\mathcal {L}^O\to \mathcal {L}^O$
such that
$f:\mathcal {L}^O\to \mathcal {L}^O$
such that
![]() $\varphi \in \mathcal {L}(\mathsf {R}(\Delta ))$
iff
$\varphi \in \mathcal {L}(\mathsf {R}(\Delta ))$
iff
![]() $f(\varphi )\in \mathcal {L}(\mathsf {R}(\Gamma ))$
. We will establish such monotonicity for sets which satisfy two requirements: First, both O and
$f(\varphi )\in \mathcal {L}(\mathsf {R}(\Gamma ))$
. We will establish such monotonicity for sets which satisfy two requirements: First, both O and
![]() $\Delta \backslash \Gamma $
are finite. Second,
$\Delta \backslash \Gamma $
are finite. Second,
![]() $O^{\leq n}p\to O^{n+1}p\in \Delta $
for some natural number n.
$O^{\leq n}p\to O^{n+1}p\in \Delta $
for some natural number n.
Proposition 2.8. If
![]() $\Gamma \subseteq \Delta \subseteq \mathcal {L}^O$
, both O and
$\Gamma \subseteq \Delta \subseteq \mathcal {L}^O$
, both O and
![]() $\Delta \backslash \Gamma $
are finite, and
$\Delta \backslash \Gamma $
are finite, and
![]() $O^{\leq n}p\to O^{n+1}p\in \Delta $
for some
$O^{\leq n}p\to O^{n+1}p\in \Delta $
for some
![]() $n\in \mathbb {N}$
, then
$n\in \mathbb {N}$
, then
![]() $\mathcal {L}(\mathsf {R}(\Delta ))$
is reducible to
$\mathcal {L}(\mathsf {R}(\Delta ))$
is reducible to
![]() $\mathcal {L}(\mathsf {R}(\Gamma ))$
.
$\mathcal {L}(\mathsf {R}(\Gamma ))$
.
Proof The required reduction can be defined as mapping every
![]() $\varphi \in \mathcal {L}^O$
to
$\varphi \in \mathcal {L}^O$
to
We show that
![]() $\varphi \in \mathcal {L}(\mathsf {R}(\Delta ))$
iff
$\varphi \in \mathcal {L}(\mathsf {R}(\Delta ))$
iff
![]() $\varphi ^*\in \mathcal {L}(\mathsf {R}(\Gamma ))$
.
$\varphi ^*\in \mathcal {L}(\mathsf {R}(\Gamma ))$
.
The “if” direction is immediate. So assume that
![]() $\varphi ^*\notin \mathcal {L}(\mathsf {R}(\Gamma ))$
. Then there is a frame
$\varphi ^*\notin \mathcal {L}(\mathsf {R}(\Gamma ))$
. Then there is a frame
![]() $\mathfrak {F}$
in
$\mathfrak {F}$
in
![]() $\mathsf {R}(\Gamma )$
and w such that
$\mathsf {R}(\Gamma )$
and w such that
![]() $\mathfrak {F},w\nVdash \varphi ^*$
. Letting
$\mathfrak {F},w\nVdash \varphi ^*$
. Letting
![]() $\mathfrak {F}_w=\langle W,R\rangle $
, note that
$\mathfrak {F}_w=\langle W,R\rangle $
, note that
![]() $\mathfrak {F}_w=\mathfrak {F}_W$
. Thus by Proposition 2.7,
$\mathfrak {F}_w=\mathfrak {F}_W$
. Thus by Proposition 2.7,
![]() $\mathfrak {F}_w$
is in
$\mathfrak {F}_w$
is in
![]() $\mathsf {R}(\Gamma )$
as well. By Proposition 2.7, it also follows that
$\mathsf {R}(\Gamma )$
as well. By Proposition 2.7, it also follows that
![]() $\mathfrak {F}_w,w\nVdash \varphi ^*$
. So, first,
$\mathfrak {F}_w,w\nVdash \varphi ^*$
. So, first,
![]() $\mathfrak {F}_w,w\Vdash O^{\leq n}\bigwedge \Delta \backslash \Gamma $
, whence with
$\mathfrak {F}_w,w\Vdash O^{\leq n}\bigwedge \Delta \backslash \Gamma $
, whence with
![]() $O^{\leq n}p\to O^{n+1}p\in \Delta $
, it follows that
$O^{\leq n}p\to O^{n+1}p\in \Delta $
, it follows that
![]() $\mathfrak {F}_w\Vdash \bigwedge \Delta \backslash \Gamma $
, and so that
$\mathfrak {F}_w\Vdash \bigwedge \Delta \backslash \Gamma $
, and so that
![]() $\mathfrak {F}_w\in \mathsf {R}(\Delta )$
. Second,
$\mathfrak {F}_w\in \mathsf {R}(\Delta )$
. Second,
![]() $\mathfrak {F}_w,w\nVdash \varphi $
, whence
$\mathfrak {F}_w,w\nVdash \varphi $
, whence
![]() $\varphi \notin \mathcal {L}(\mathsf {R}(\Delta ))$
.
$\varphi \notin \mathcal {L}(\mathsf {R}(\Delta ))$
.
From this proposition, we obtain the partial axiomatizability boundary among unimodal logics mentioned above: If
![]() $\Lambda $
is a normal unimodal logic and
$\Lambda $
is a normal unimodal logic and
![]() $\Gamma $
is a finite set of
$\Gamma $
is a finite set of
![]() $\mathcal {L}^{\Box }_{\mathrm {qf}}$
-formulas such that
$\mathcal {L}^{\Box }_{\mathrm {qf}}$
-formulas such that
![]() $\Box ^{\leq n}p\to \Box ^{n+1}p\in \Lambda +\Gamma $
, then
$\Box ^{\leq n}p\to \Box ^{n+1}p\in \Lambda +\Gamma $
, then
![]() $\Lambda \pi +$
is recursively enumerable (decidable) only if
$\Lambda \pi +$
is recursively enumerable (decidable) only if
![]() $(\Lambda +\Gamma )\pi +$
is recursively enumerable (decidable) as well. This includes the majority of logics included in Figure 1; note in particular that every extension of
$(\Lambda +\Gamma )\pi +$
is recursively enumerable (decidable) as well. This includes the majority of logics included in Figure 1; note in particular that every extension of
![]() $\mathrm {K4}$
contains
$\mathrm {K4}$
contains
![]() $\Box p\to \Box \Box p$
, and every extension of
$\Box p\to \Box \Box p$
, and every extension of
![]() $\mathrm {KE}$
contains
$\mathrm {KE}$
contains
![]() $\Box \Box p\to \Box \Box \Box p$
, as is easy to see using the completeness of
$\Box \Box p\to \Box \Box \Box p$
, as is easy to see using the completeness of
![]() $\mathrm {KE}$
with respect to relational frames with a Euclidean accessibility relation.
$\mathrm {KE}$
with respect to relational frames with a Euclidean accessibility relation.
It is natural to ask whether the two constraints on sets of formulas in Proposition 2.8 are essential. We will later see that the requirement of finiteness of
![]() $\Delta \backslash \Gamma $
cannot be dropped completely, or weakened to recursively enumerable sets of axioms, even among sets of quantifier-free formulas; see Proposition 5.9. We leave open the question whether the requirement of finiteness can be weakened to decidability, as well as the question whether the assumption of containing
$\Delta \backslash \Gamma $
cannot be dropped completely, or weakened to recursively enumerable sets of axioms, even among sets of quantifier-free formulas; see Proposition 5.9. We leave open the question whether the requirement of finiteness can be weakened to decidability, as well as the question whether the assumption of containing
![]() $O^{\leq n}p\to O^{n+1}p\in \Delta $
for some
$O^{\leq n}p\to O^{n+1}p\in \Delta $
for some
![]() $n\in \mathbb {N}$
can be dropped or weakened.
$n\in \mathbb {N}$
can be dropped or weakened.
2.4 Second-order logic
Most of the complexity results to be established proceed by finding a reduction between
![]() $\mathcal {L}^O$
over a class of relational frames and a suitable form of second-order logic over such frames. We assume familiarity with second-order logic and its standard semantics; for a detailed exposition, see [Reference Shapiro53].
$\mathcal {L}^O$
over a class of relational frames and a suitable form of second-order logic over such frames. We assume familiarity with second-order logic and its standard semantics; for a detailed exposition, see [Reference Shapiro53].
The most basic case is that of monadic second-order logic. Given a countably infinite set of first-order variables
![]() $\Psi $
and a disjoint set of second-order variables
$\Psi $
and a disjoint set of second-order variables
![]() $\Omega $
, the language
$\Omega $
, the language
![]() $\mathcal {M}^O$
of monadic second-order logic (over O) is defined in BNF as follows:
$\mathcal {M}^O$
of monadic second-order logic (over O) is defined in BNF as follows:
where
![]() $x\in \Psi $
and
$x\in \Psi $
and
![]() $X\in \Omega $
. Formulas of
$X\in \Omega $
. Formulas of
![]() $\varphi $
can straightforwardly be interpreted over a relational frame
$\varphi $
can straightforwardly be interpreted over a relational frame
![]() $\mathfrak {F}$
, with individual quantifiers ranging over worlds, and monadic second-order quantifiers ranging over sets of worlds. We adapt the notation used above for
$\mathfrak {F}$
, with individual quantifiers ranging over worlds, and monadic second-order quantifiers ranging over sets of worlds. We adapt the notation used above for
![]() $\mathcal {L}^O$
, writing
$\mathcal {L}^O$
, writing
![]() $\mathfrak {F},a\Vdash \varphi $
for the truth of
$\mathfrak {F},a\Vdash \varphi $
for the truth of
![]() $\varphi $
in
$\varphi $
in
![]() $\mathfrak {F}$
relative to an assignment function a (on
$\mathfrak {F}$
relative to an assignment function a (on
![]() $\Psi \cup \Omega $
), and
$\Psi \cup \Omega $
), and
![]() $\mathfrak {F}\Vdash \varphi $
for
$\mathfrak {F}\Vdash \varphi $
for
![]() $\varphi $
being valid on
$\varphi $
being valid on
![]() $\mathfrak {F}$
, i.e., true relative to every assignment function. Similarly, for a set
$\mathfrak {F}$
, i.e., true relative to every assignment function. Similarly, for a set
![]() $\Gamma \subseteq \mathcal {M}^O$
, we write
$\Gamma \subseteq \mathcal {M}^O$
, we write
![]() $\mathsf {R}(\Gamma )$
for the class of relational frames validating every member of
$\mathsf {R}(\Gamma )$
for the class of relational frames validating every member of
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $\mathcal {M}(\mathsf {C})$
for the set of
$\mathcal {M}(\mathsf {C})$
for the set of
![]() $\mathcal {M}^O$
-formulas valid on every frame in
$\mathcal {M}^O$
-formulas valid on every frame in
![]() $\mathsf {C}$
. The analogous conventions will be adopted for the other versions of second-order logic discussed below; we won’t remark on this separately.
$\mathsf {C}$
. The analogous conventions will be adopted for the other versions of second-order logic discussed below; we won’t remark on this separately.
Monadic second-order logic arises naturally when one extends the well-known standard translation of propositional modal logic to propositional quantifiers. For a discussion of the standard translation in the quantifier-free setting, see [Reference Blackburn, de Rijke and Venema4, Section 2.4]. The standard translation maps every propositional modal formula
![]() $\varphi $
to a corresponding first-order formula
$\varphi $
to a corresponding first-order formula
![]() $\varphi ^x$
in which no first-order variable other than x is free. This is can be extended to propositional quantifiers by translating them as monadic second-order quantifiers. Assuming that for every propositional variable p, there is a distinct monadic second-order variable
$\varphi ^x$
in which no first-order variable other than x is free. This is can be extended to propositional quantifiers by translating them as monadic second-order quantifiers. Assuming that for every propositional variable p, there is a distinct monadic second-order variable
![]() $X_p$
, this leads to the recursive mapping from
$X_p$
, this leads to the recursive mapping from
![]() $\mathcal {L}^O$
to
$\mathcal {L}^O$
to
![]() $\mathcal {M}^O$
whose only non-trivial clauses are the following:
$\mathcal {M}^O$
whose only non-trivial clauses are the following:
 $$ \begin{align*} p^x&:=X_px, \\ (\forall p\varphi)^x&:=\forall X_p(\varphi^x), \\ (\Box\varphi)^x&:=\forall y(R_{\Box} xy\to\varphi^y). \end{align*} $$
$$ \begin{align*} p^x&:=X_px, \\ (\forall p\varphi)^x&:=\forall X_p(\varphi^x), \\ (\Box\varphi)^x&:=\forall y(R_{\Box} xy\to\varphi^y). \end{align*} $$
As in the case without propositional quantifiers, a formula
![]() $\varphi \in \mathcal {L}^O$
is true in a world of a frame, relative to an assignment function, just in case
$\varphi \in \mathcal {L}^O$
is true in a world of a frame, relative to an assignment function, just in case
![]() $\varphi ^x$
is true in that frame relative to a corresponding assignment function which interprets the first-order variable x as w. We can then state the fundamental result on the standard translation as follows:
$\varphi ^x$
is true in that frame relative to a corresponding assignment function which interprets the first-order variable x as w. We can then state the fundamental result on the standard translation as follows:
Proposition 2.9. Let
![]() $\mathfrak {F}$
be a relational frame, w a world, a an assignment function on propositional variables, and b an assignment function on first- and monadic second-order variables such that
$\mathfrak {F}$
be a relational frame, w a world, a an assignment function on propositional variables, and b an assignment function on first- and monadic second-order variables such that
![]() $b(X_p)=a(p)$
for all
$b(X_p)=a(p)$
for all
![]() $i\in \mathbb {N}$
. Then,
$i\in \mathbb {N}$
. Then,
Proof By a routine induction on the complexity of
![]() $\varphi $
.
$\varphi $
.
The standard translation brings out that propositionally quantified modal logic interpreted over relational frames can be thought of as a fragment of monadic second-order logic with binary relational constants. This is why it is sometimes called second-order propositional modal logic, e.g., by Kaminski and Tiomkin [Reference Kaminski and Tiomkin26]. In fact, already the study of propositional modal logic without propositional quantifiers over classes of relational frames involves a monadic second-order element: A quantifier-free formula
![]() $\varphi $
is valid in a world of a frame just in case its universal closure
$\varphi $
is valid in a world of a frame just in case its universal closure
![]() $\bar {\forall }\varphi $
is true in that world (independently of the assignment function). Because of this implicit second-order aspect, various sets
$\bar {\forall }\varphi $
is true in that world (independently of the assignment function). Because of this implicit second-order aspect, various sets
![]() $\Gamma \subseteq \mathcal {L}^{\Box }_{\mathrm {qf}}$
, such as the singletons of
$\Gamma \subseteq \mathcal {L}^{\Box }_{\mathrm {qf}}$
, such as the singletons of
![]() $\mathbf {M}$
and
$\mathbf {M}$
and
![]() $\mathbf {W}$
, define classes of relational frames
$\mathbf {W}$
, define classes of relational frames
![]() $\mathsf {R}(\Gamma )$
which are not first-order definable. This aspect of propositional modal logic is further discussed by Hughes and Cresswell [Reference Hughes and Cresswell25, pp. 188–189] and Blackburn et al. [Reference Blackburn, de Rijke and Venema4, Section 3.2].
$\mathsf {R}(\Gamma )$
which are not first-order definable. This aspect of propositional modal logic is further discussed by Hughes and Cresswell [Reference Hughes and Cresswell25, pp. 188–189] and Blackburn et al. [Reference Blackburn, de Rijke and Venema4, Section 3.2].
An immediate consequence of Proposition 2.9 is that for any class of relational frames
![]() $\mathsf {C}$
,
$\mathsf {C}$
,
![]() $\mathcal {L}(\mathsf {C})$
is reducible to
$\mathcal {L}(\mathsf {C})$
is reducible to
![]() $\mathcal {M}(\mathsf {C})$
. Thus, the decidability of the former follows from the decidability of the latter. This connection will form the basis of many of the decidability results to be presented. (This is a common approach to decidability results in modal logic; see [Reference Blackburn, de Rijke and Venema4, Section 6.3] for examples in the quantifier-free setting, and [Reference Zach58] for an example including propositional quantifiers.) In some cases, we can simply appeal to known results on the decidability of monadic second-order logic over classes of relational frames (see [Reference Gurevich, Barwise and Feferman19] for an overview of results in this area). In other cases, we will establish some new limitative results concerning monadic second-order logic.
$\mathcal {M}(\mathsf {C})$
. Thus, the decidability of the former follows from the decidability of the latter. This connection will form the basis of many of the decidability results to be presented. (This is a common approach to decidability results in modal logic; see [Reference Blackburn, de Rijke and Venema4, Section 6.3] for examples in the quantifier-free setting, and [Reference Zach58] for an example including propositional quantifiers.) In some cases, we can simply appeal to known results on the decidability of monadic second-order logic over classes of relational frames (see [Reference Gurevich, Barwise and Feferman19] for an overview of results in this area). In other cases, we will establish some new limitative results concerning monadic second-order logic.
The new limitative results can be simplified by using an obvious notational variant of monadic second-order logic which dispenses with first-order quantifiers. First-order quantifiers can be simulated using monadic second-order quantification over singleton sets if we admit two new kinds of atomic formulas. (See, e.g., [Reference Gurevich, Barwise and Feferman19, p. 482] for a similar variant; the present version is chosen so as to harmonize with
![]() $\mathcal {L}^O$
, but the differences are immaterial.) The variant monadic second-order language
$\mathcal {L}^O$
, but the differences are immaterial.) The variant monadic second-order language
![]() $\mathcal {N}^O$
is defined in BNF as follows:
$\mathcal {N}^O$
is defined in BNF as follows:
where
![]() $X\in \Omega $
. The truth-conditions for the new (non-standard) atomic formulas are as follows:
$X\in \Omega $
. The truth-conditions for the new (non-standard) atomic formulas are as follows:
-
 $\mathfrak {F},a\Vdash X\subseteq Y$
iff
$\mathfrak {F},a\Vdash X\subseteq Y$
iff
 $a(X)\subseteq a(Y),$
$a(X)\subseteq a(Y),$
-
 $\mathfrak {F},a\Vdash R_{\Box } XY$
iff for all
$\mathfrak {F},a\Vdash R_{\Box } XY$
iff for all
 $x\in a(X)$
there is some
$x\in a(X)$
there is some
 $y\in a(Y)$
such that
$y\in a(Y)$
such that
 $xR_{\Box } y.$
$xR_{\Box } y.$
![]() $\mathcal {M}^O$
and
$\mathcal {M}^O$
and
![]() $\mathcal {N}^O$
are intertranslatable: Assume that for every variable
$\mathcal {N}^O$
are intertranslatable: Assume that for every variable
![]() $\xi \in \Psi \cup \Omega $
,
$\xi \in \Psi \cup \Omega $
,
![]() $X_{\xi }$
is a distinct variable of
$X_{\xi }$
is a distinct variable of
![]() $\Omega $
, and consider the recursive mappings
$\Omega $
, and consider the recursive mappings
![]() $\nu :\mathcal {M}^O\to \mathcal {N}^O$
and
$\nu :\mathcal {M}^O\to \mathcal {N}^O$
and
![]() $\mu :\mathcal {N}^O\to \mathcal {M}^O$
whose only non-trivial clauses are the following:
$\mu :\mathcal {N}^O\to \mathcal {M}^O$
whose only non-trivial clauses are the following:
 $$ \begin{align*} \begin{array}{ll} \nu(Xx):=X_x\subseteq X_X, & \mu(X\subseteq Y):=\forall x(Xx\to Yx), \\ \nu(R_{\Box} xy):=R_{\Box} X_xX_y, &\mu(R_{\Box} XY):=\forall x(Xx\to\exists y(Yy\wedge R_{\Box} xy)), \\ \nu(\forall x\varphi):=\forall X_x(\mathrm{sing}(X_x)\to\nu(\varphi)), & \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} \nu(Xx):=X_x\subseteq X_X, & \mu(X\subseteq Y):=\forall x(Xx\to Yx), \\ \nu(R_{\Box} xy):=R_{\Box} X_xX_y, &\mu(R_{\Box} XY):=\forall x(Xx\to\exists y(Yy\wedge R_{\Box} xy)), \\ \nu(\forall x\varphi):=\forall X_x(\mathrm{sing}(X_x)\to\nu(\varphi)), & \end{array} \end{align*} $$
where
![]() $\mathrm {sing}(X)$
states that X is a singleton, which can be defined as follows:
$\mathrm {sing}(X)$
states that X is a singleton, which can be defined as follows:
-
 $\mathrm {empty}(X):=\forall Y(X\subseteq Y)$
,
$\mathrm {empty}(X):=\forall Y(X\subseteq Y)$
, -
 $\mathrm {sing}(X):=\neg \mathrm {empty}(X)\wedge \forall Y(Y\subseteq X\to \mathrm {empty}(Y)\vee X\subseteq Y)$
.
$\mathrm {sing}(X):=\neg \mathrm {empty}(X)\wedge \forall Y(Y\subseteq X\to \mathrm {empty}(Y)\vee X\subseteq Y)$
.
It is easy to see that along a result analogous to Proposition 2.9,
![]() $\mathcal {M}(\mathsf {C})$
is recursively isomorphic to
$\mathcal {M}(\mathsf {C})$
is recursively isomorphic to
![]() $\mathcal {N}(\mathsf {C})$
, for any class of relational frames. For present purposes, we can therefore treat
$\mathcal {N}(\mathsf {C})$
, for any class of relational frames. For present purposes, we can therefore treat
![]() $\mathcal {M}^O$
and
$\mathcal {M}^O$
and
![]() $\mathcal {N}^O$
as notational variants of monadic second-order logic, and so interchangeable.
$\mathcal {N}^O$
as notational variants of monadic second-order logic, and so interchangeable.
Monadic second-order logic will also play a role in establishing unaxiomatizability results. For this, we now note that on certain classes of relational frames, the standard translation can be reversed, and monadic second-order logic can conversely be thought of as a fragment of propositionally quantified modal logic. We establish this for point-generated unimodal frames with a transitive accessibility relation. The observation will be especially easy to show using the variant monadic second-order language
![]() $\mathcal {N}^{\Box }$
. We call the relevant function the “backwards translation.” Assuming that for every propositional variable
$\mathcal {N}^{\Box }$
. We call the relevant function the “backwards translation.” Assuming that for every propositional variable
![]() $p\in \Phi $
, there is a distinct second-order variable
$p\in \Phi $
, there is a distinct second-order variable
![]() $X_p\in \Omega $
, it is the recursive mapping
$X_p\in \Omega $
, it is the recursive mapping
![]() $\cdot ^{\leftarrow }:\mathcal {N}^{\Box }\to \mathcal {L}^{\Box }$
whose only non-trivial clauses are the following:
$\cdot ^{\leftarrow }:\mathcal {N}^{\Box }\to \mathcal {L}^{\Box }$
whose only non-trivial clauses are the following:
 $$ \begin{align*} (X\subseteq Y)^{\leftarrow}&:=\Box(p_X\to p_Y), \\ (RXY)^{\leftarrow}&:=\Box(p_X\to\Diamond p_Y), \\ (\forall X\varphi)^{\leftarrow}&:=\forall p_X(\varphi^{\leftarrow}). \end{align*} $$
$$ \begin{align*} (X\subseteq Y)^{\leftarrow}&:=\Box(p_X\to p_Y), \\ (RXY)^{\leftarrow}&:=\Box(p_X\to\Diamond p_Y), \\ (\forall X\varphi)^{\leftarrow}&:=\forall p_X(\varphi^{\leftarrow}). \end{align*} $$
Analogous to Proposition 2.9, we can show:
Proposition 2.10. Let
![]() $\mathfrak {F}=\langle W,R\rangle $
be a relational frame, R be transitive,
$\mathfrak {F}=\langle W,R\rangle $
be a relational frame, R be transitive,
![]() $w\in W$
, and
$w\in W$
, and
![]() $\varphi \in \mathcal {N}^{\Box }$
. For every second-order assignment function a on
$\varphi \in \mathcal {N}^{\Box }$
. For every second-order assignment function a on
![]() $\mathfrak {F}_w$
,
$\mathfrak {F}_w$
,
where
![]() $b(p_X)=a(X)$
for all
$b(p_X)=a(X)$
for all
![]() $X\in \Omega $
.
$X\in \Omega $
.
Proof By induction on the complexity of
![]() $\varphi $
.
$\varphi $
.
Thus, if
![]() $\mathsf {C}$
is a class of point-generated unimodal frames with a transitive accessibility relation, then
$\mathsf {C}$
is a class of point-generated unimodal frames with a transitive accessibility relation, then
![]() $\mathcal {N}(\mathsf {C})$
, and so also
$\mathcal {N}(\mathsf {C})$
, and so also
![]() $\mathcal {M}(\mathsf {C})$
, is reducible to
$\mathcal {M}(\mathsf {C})$
, is reducible to
![]() $\mathcal {L}(\mathsf {C})$
. We can therefore show that
$\mathcal {L}(\mathsf {C})$
. We can therefore show that
![]() $\mathcal {L}(\mathsf {C})$
is not axiomatizable by showing that
$\mathcal {L}(\mathsf {C})$
is not axiomatizable by showing that
![]() $\mathcal {M}(\mathsf {C})$
is not axiomatizable. We will employ this method for certain classes of frames. For other classes of frames, we devise a more ad hoc translation from
$\mathcal {M}(\mathsf {C})$
is not axiomatizable. We will employ this method for certain classes of frames. For other classes of frames, we devise a more ad hoc translation from
![]() $\mathcal {L}(\mathsf {C})$
, not to monadic second-order logic over
$\mathcal {L}(\mathsf {C})$
, not to monadic second-order logic over
![]() $\mathsf {C}$
, but to full second-order logic (which we also simply call second-order logic). In its usual presentation, (full) second-order logic provides n-ary variables for all
$\mathsf {C}$
, but to full second-order logic (which we also simply call second-order logic). In its usual presentation, (full) second-order logic provides n-ary variables for all
![]() $n\in \mathbb {N}$
, which are interpreted using n-ary relations. However, similar to the case of
$n\in \mathbb {N}$
, which are interpreted using n-ary relations. However, similar to the case of
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
, second-order logic can be shown to be intertranslatable with a seemingly more restricted language, and it will greatly simplify some of the following exposition to work with this latter language. The language, which we call
$\mathcal {N}$
, second-order logic can be shown to be intertranslatable with a seemingly more restricted language, and it will greatly simplify some of the following exposition to work with this latter language. The language, which we call
![]() $\mathcal {S}$
, employs only binary second-order variables, and no non-logical constants; its syntax is specified in BNF as follows:
$\mathcal {S}$
, employs only binary second-order variables, and no non-logical constants; its syntax is specified in BNF as follows:
where
![]() $x\in \Psi $
and
$x\in \Psi $
and
![]() $X\in \Omega $
. (While elements of
$X\in \Omega $
. (While elements of
![]() $\Omega $
serve as monadic second-order variables in
$\Omega $
serve as monadic second-order variables in
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
, they serve as binary second-order variables in
$\mathcal {N}$
, they serve as binary second-order variables in
![]() $\mathcal {S}$
. Below, it will always be clear which of these languages is used, and so it will always be clear whether a given member of
$\mathcal {S}$
. Below, it will always be clear which of these languages is used, and so it will always be clear whether a given member of
![]() $\Omega $
is used as a monadic or as a binary variable.)
$\Omega $
is used as a monadic or as a binary variable.)
Crucially, the variant second-order language
![]() $\mathcal {S}$
is not only syntactically restricted, but also interprets binary second-order quantifiers as restricted to symmetric relations. To emphasize this, we state the truth-conditions of such quantifiers explicitly, for any set D (since
$\mathcal {S}$
is not only syntactically restricted, but also interprets binary second-order quantifiers as restricted to symmetric relations. To emphasize this, we state the truth-conditions of such quantifiers explicitly, for any set D (since
![]() $\mathcal {S}$
has no non-logical constants, its models are simply sets):
$\mathcal {S}$
has no non-logical constants, its models are simply sets):
-
 $D,a\Vdash \forall X\varphi $
iff
$D,a\Vdash \forall X\varphi $
iff
 $D,a[S/X]\Vdash \varphi $
for all symmetric relations
$D,a[S/X]\Vdash \varphi $
for all symmetric relations
 $S\subseteq D^2$
.
$S\subseteq D^2$
.
The more general quantifiers of second-order logic as standardly defined can be simulated using this more restricted form of binary second-order quantification, as shown by Rabin and Scott in work presented by Nerode and Shore [Reference Nerode and Shore41]. For present purposes, we can therefore treat
![]() $\mathcal {S}$
as a notational variant of second-order logic. To emphasize the restricted interpretation of second-order quantifiers, we call it symmetric second-order logic, and write ssol for the set of its validities, i.e., the formulas of
$\mathcal {S}$
as a notational variant of second-order logic. To emphasize the restricted interpretation of second-order quantifiers, we call it symmetric second-order logic, and write ssol for the set of its validities, i.e., the formulas of
![]() $\mathcal {S}$
valid on all sets.
$\mathcal {S}$
valid on all sets.
3 Decidability
The main existing decidability result for propositionally quantified modal logics is the decidability of
![]() $\mathrm {S5}\pi +$
, which was established by Kaplan [Reference Kaplan27] and Fine [Reference Fine12]. Fine notes two ways of obtaining this result: The first uses a quantifier-elimination result for
$\mathrm {S5}\pi +$
, which was established by Kaplan [Reference Kaplan27] and Fine [Reference Fine12]. Fine notes two ways of obtaining this result: The first uses a quantifier-elimination result for
![]() $\mathrm {S5}\pi +$
, a version of which is also established by Kaplan. This technique also plays a role in the proof of the decidability of
$\mathrm {S5}\pi +$
, a version of which is also established by Kaplan. This technique also plays a role in the proof of the decidability of
![]() $\mathrm {KD4E}\pi +$
by Ding [Reference Ding10]. The other way of establishing the decidability of
$\mathrm {KD4E}\pi +$
by Ding [Reference Ding10]. The other way of establishing the decidability of
![]() $\mathrm {S5}\pi +$
, discussed by both Kaplan [Reference Kaplan27] and Fine [Reference Fine12], proceeds by reducing
$\mathrm {S5}\pi +$
, discussed by both Kaplan [Reference Kaplan27] and Fine [Reference Fine12], proceeds by reducing
![]() $\mathrm {S5}\pi +$
to monadic second-order logic (without non-logical constants), which is known to be decidable. The more general technique developed in this section is inspired by this second method.
$\mathrm {S5}\pi +$
to monadic second-order logic (without non-logical constants), which is known to be decidable. The more general technique developed in this section is inspired by this second method.
3.1 Frames of finitely bounded size
With the basic concepts introduced in the previous section, the decidability of
![]() $\mathrm {S5}\pi +$
is straightforward:
$\mathrm {S5}\pi +$
is straightforward:
![]() $\mathsf {R}(\mathrm {S5})$
is the class of unimodal frames whose accessibility relation is an equivalence relation. The accessibility relation of any point-generated subframe of such a frame is universal, so by Proposition 2.7,
$\mathsf {R}(\mathrm {S5})$
is the class of unimodal frames whose accessibility relation is an equivalence relation. The accessibility relation of any point-generated subframe of such a frame is universal, so by Proposition 2.7,
![]() $\mathrm {S5}\pi +$
is the propositionally quantified modal logic of relational frames with a universal accessibility relation. Using the standard translation and Proposition 2.9, we can think of this logic as a fragment of monadic second-order logic over such frames. But on such frames, atomic formulas of the form
$\mathrm {S5}\pi +$
is the propositionally quantified modal logic of relational frames with a universal accessibility relation. Using the standard translation and Proposition 2.9, we can think of this logic as a fragment of monadic second-order logic over such frames. But on such frames, atomic formulas of the form
![]() $Rxy$
are trivially true. Monadic second-order logic over such frames is therefore recursively isomorphic to monadic second-order logic without non-logical constants, models of which are simply sets. And the latter logic is well-known to be decidable; in fact, its decidability follows from results already obtained by Löwenheim [Reference Löwenheim37].
$Rxy$
are trivially true. Monadic second-order logic over such frames is therefore recursively isomorphic to monadic second-order logic without non-logical constants, models of which are simply sets. And the latter logic is well-known to be decidable; in fact, its decidability follows from results already obtained by Löwenheim [Reference Löwenheim37].
It will suffice to give just a sketch of a proof of this result: For simplicity, we work with the variant monadic second-order language
![]() $\mathcal {N}$
. First, we note that it suffices to show that every satisfiable monadic second-order formula without non-logical constants is satisfiable on a model whose size is bounded by some finite number which is computable in terms of the complexity of the formula: with this, the validity of a formula
$\mathcal {N}$
. First, we note that it suffices to show that every satisfiable monadic second-order formula without non-logical constants is satisfiable on a model whose size is bounded by some finite number which is computable in terms of the complexity of the formula: with this, the validity of a formula
![]() $\varphi $
can be determined by a finite computation, considering just the models of such bounded size, which are finite in number up to isomorphism. This finite bound on models is obtained in terms of the quantifier depth
$\varphi $
can be determined by a finite computation, considering just the models of such bounded size, which are finite in number up to isomorphism. This finite bound on models is obtained in terms of the quantifier depth
![]() $\mathrm {qd}(\varphi )$
of
$\mathrm {qd}(\varphi )$
of
![]() $\varphi $
, where the definition of quantifier depth for formulas of
$\varphi $
, where the definition of quantifier depth for formulas of
![]() $\mathcal {N}^O$
is straightforwardly adapted from Definition 2.5. The crucial insight is the following: As noted, a model for monadic second-order logic without non-logical constants is simply a set; therefore, in assigning values to variables, it only matters how these values are related by the subset relation. And given n variables, any such constellation of subset relationships can be exhibited in a set of size
$\mathcal {N}^O$
is straightforwardly adapted from Definition 2.5. The crucial insight is the following: As noted, a model for monadic second-order logic without non-logical constants is simply a set; therefore, in assigning values to variables, it only matters how these values are related by the subset relation. And given n variables, any such constellation of subset relationships can be exhibited in a set of size
![]() $2^n$
. (Related considerations were also used by Parry [Reference Parry42] to show the decidability of
$2^n$
. (Related considerations were also used by Parry [Reference Parry42] to show the decidability of
![]() $\mathrm {S5}$
.)
$\mathrm {S5}$
.)
This idea can be turned into a more rigorous proof using the technique of Ehrenfeucht–Fraïssé games, as noted by Väänänen [Reference Väänänen and Zalta56, Section 8], or their variant presentation as back and forth systems. These techniques allow us to show that a formula up to certain quantifier depth n is true in one model if and only if it is true in another model, connected to the first by a back-and-forth system; in the present case, a model (i.e., set) of size greater than
![]() $2^n$
and a model (set) of size
$2^n$
and a model (set) of size
![]() $2^n$
. Below, we therefore adapt back and forth systems to the variant monadic second-order language
$2^n$
. Below, we therefore adapt back and forth systems to the variant monadic second-order language
![]() $\mathcal {N}^O$
.
$\mathcal {N}^O$
.
In the relational frames we will be interested in, two worlds will not in general be interchangeable. But using back and forth systems, we will at least be able to reduce any cluster of duplicate worlds to a finite number determined by the quantifier depth of the formula under consideration. Combined with taking point-generated subframes, this gives us a flexible method for reducing the size of relational frames in a given class without changing the satisfiability of any propositionally quantified modal formula of a given complexity. In many interesting cases, we will be able to impose a finite bound on the size of the resulting frame which is computable in terms of this complexity, and this allows us to prove decidability of the relevant propositionally quantified modal logic.
We first make precise how such a bound on the size of relational frames entails decidability. To start, we introduce the notion of two frames validating the same closed monadic second-order formulas up to quantifier depth n, which we call being n-equivalent. We will be interested in classes of frames which contain, for every point-generated subframe of one of their frames, an n-equivalent frame of a size that is computably finitely bounded in terms of n; we call these computably reducible.
Definition 3.1. For any
![]() $n\in \mathbb {N}$
, relational frames
$n\in \mathbb {N}$
, relational frames
![]() $\mathfrak {F}$
and
$\mathfrak {F}$
and
![]() $\mathfrak {F}'$
are n-equivalent, written
$\mathfrak {F}'$
are n-equivalent, written
![]() $\mathfrak {F}\equiv _n\mathfrak {F}'$
, if for all closed formulas
$\mathfrak {F}\equiv _n\mathfrak {F}'$
, if for all closed formulas
![]() $\varphi \in \mathcal {N}^O$
of quantifier depth
$\varphi \in \mathcal {N}^O$
of quantifier depth
![]() $\leq n$
,
$\leq n$
,
![]() $\mathfrak {F}\Vdash \varphi $
iff
$\mathfrak {F}\Vdash \varphi $
iff
![]() $\mathfrak {F}'\Vdash \varphi $
.
$\mathfrak {F}'\Vdash \varphi $
.
Let
![]() $\mathsf {C}$
be a class of relational frames.
$\mathsf {C}$
be a class of relational frames.
-
• For any
 $r:\mathbb {N}\to \mathbb {N}$
,
$r:\mathbb {N}\to \mathbb {N}$
,
 $\mathsf {C}$
is r-reducible if for every
$\mathsf {C}$
is r-reducible if for every
 $n\in \mathbb {N}$
, every point-generated subframe of a frame in
$n\in \mathbb {N}$
, every point-generated subframe of a frame in
 $\mathsf {C}$
is n-equivalent to some frame in
$\mathsf {C}$
is n-equivalent to some frame in
 $\mathsf {C}$
of size
$\mathsf {C}$
of size
 $\leq r(n)$
.
$\leq r(n)$
. -
•
 $\mathsf {C}$
is computably reducible if
$\mathsf {C}$
is computably reducible if
 $\mathsf {C}$
is r-reducible for some computable function
$\mathsf {C}$
is r-reducible for some computable function
 $r:\mathbb {N}\to \mathbb {N}$
.
$r:\mathbb {N}\to \mathbb {N}$
.
We can now show that computably reducible classes of frames defined by finite sets of formulas give rise to decidable propositionally quantified modal logics. The proof is an instance of a standard type of decidability argument; for further details on this type of argument in the quantifier-free case, see [Reference Blackburn, de Rijke and Venema4, Section 6.2, esp. Theorem 6.7 on p. 342].
Lemma 3.2. If
![]() $\Gamma \subseteq \mathcal {L}^O$
is finite and
$\Gamma \subseteq \mathcal {L}^O$
is finite and
![]() $\mathsf {R}(\Gamma )$
is computably reducible, then
$\mathsf {R}(\Gamma )$
is computably reducible, then
![]() $\mathcal {L}(\mathsf {R}(\Gamma ))$
is decidable.
$\mathcal {L}(\mathsf {R}(\Gamma ))$
is decidable.
Proof Assume
![]() $\mathsf {R}(\Gamma )$
is r-reducible for some computable function
$\mathsf {R}(\Gamma )$
is r-reducible for some computable function
![]() $r:\mathbb {N}\to \mathbb {N}$
. If
$r:\mathbb {N}\to \mathbb {N}$
. If
![]() $\varphi \in \mathcal {L}^O$
is satisfiable in a frame in
$\varphi \in \mathcal {L}^O$
is satisfiable in a frame in
![]() $\mathsf {R}(\Gamma )$
, then by Proposition 2.7, it is satisfiable in one of its point-generated subframes
$\mathsf {R}(\Gamma )$
, then by Proposition 2.7, it is satisfiable in one of its point-generated subframes
![]() $\mathfrak {F}$
. Let n be the quantifier depth of
$\mathfrak {F}$
. Let n be the quantifier depth of
![]() $\nu (\varphi ^{x})$
, the translation of
$\nu (\varphi ^{x})$
, the translation of
![]() $\varphi $
in
$\varphi $
in
![]() $\mathcal {N}^O$
. Then there is a frame
$\mathcal {N}^O$
. Then there is a frame
![]() $\mathfrak {F}'$
in
$\mathfrak {F}'$
in
![]() $\mathsf {R}(\Gamma )$
of size
$\mathsf {R}(\Gamma )$
of size
![]() $\leq r(n)$
which is n-equivalent to
$\leq r(n)$
which is n-equivalent to
![]() $\mathfrak {F}$
, whence
$\mathfrak {F}$
, whence
![]() $\varphi $
is satisfiable on
$\varphi $
is satisfiable on
![]() $\mathfrak {F}'$
.
$\mathfrak {F}'$
.
Consequently, the satisfiability (or, correspondingly, validity) of any formula
![]() $\varphi $
can be determined by considering only frames in
$\varphi $
can be determined by considering only frames in
![]() $\mathsf {R}(\Gamma )$
up to the finite size
$\mathsf {R}(\Gamma )$
up to the finite size
![]() $r(\mathrm {qd}(\nu (\varphi ^x)))$
. Since r is a computable function, this bound is computable in terms of
$r(\mathrm {qd}(\nu (\varphi ^x)))$
. Since r is a computable function, this bound is computable in terms of
![]() $\varphi $
. Up to isomorphism, there are only finitely many such frames. Since
$\varphi $
. Up to isomorphism, there are only finitely many such frames. Since
![]() $\Gamma $
is finite, and the validity of a formula on a finite frame is decidable, the finite frames in
$\Gamma $
is finite, and the validity of a formula on a finite frame is decidable, the finite frames in
![]() $\mathsf {R}(\Gamma )$
are recursively enumerable. It follows that
$\mathsf {R}(\Gamma )$
are recursively enumerable. It follows that
![]() $\mathcal {L}(\mathsf {R}(\Gamma ))$
is decidable.
$\mathcal {L}(\mathsf {R}(\Gamma ))$
is decidable.
3.2 Diversity
In this section, we make precise the notion of worlds of a relational frame being duplicates: worlds w and v are duplicates if the structure of the frame is invariant under interchanging w and v, i.e., if the transposition
![]() $(wv)$
(the permutation of worlds mapping w and v to each other, and every other world to itself) is an automorphism of the frame (i.e., an isomorphism from the frame to itself). The relation of being a duplicate is an equivalence relation, dividing the frame into classes of interchangeable worlds. Without changing the validity of a given formula of a given syntactic complexity, each of these classes can be reduced to a certain finite number of worlds. Therefore, the number of these classes will play an important role; we call it the frame’s diversity.
$(wv)$
(the permutation of worlds mapping w and v to each other, and every other world to itself) is an automorphism of the frame (i.e., an isomorphism from the frame to itself). The relation of being a duplicate is an equivalence relation, dividing the frame into classes of interchangeable worlds. Without changing the validity of a given formula of a given syntactic complexity, each of these classes can be reduced to a certain finite number of worlds. Therefore, the number of these classes will play an important role; we call it the frame’s diversity.
Definition 3.3. Let
![]() $\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
be a relational frame.
$\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
be a relational frame.
![]() $w\in W$
is a duplicate of
$w\in W$
is a duplicate of
![]() $v\in W$
if
$v\in W$
if
![]() $(wv)$
is an automorphism of
$(wv)$
is an automorphism of
![]() $\mathfrak {F}$
.
$\mathfrak {F}$
.
![]() $\triangle _{\mathfrak {F}}$
is the relation of being a duplicate on
$\triangle _{\mathfrak {F}}$
is the relation of being a duplicate on
![]() $\mathfrak {F}$
, i.e.,
$\mathfrak {F}$
, i.e.,
A duplicate class of
![]() $\mathfrak {F}$
is an equivalence class of
$\mathfrak {F}$
is an equivalence class of
![]() $\triangle _{\mathfrak {F}}$
. The diversity of
$\triangle _{\mathfrak {F}}$
. The diversity of
![]() $\mathfrak {F}$
, written
$\mathfrak {F}$
, written
![]() $\Delta (\mathfrak {F})$
is the number of duplicate classes of
$\Delta (\mathfrak {F})$
is the number of duplicate classes of
![]() $\mathfrak {F}$
:
$\mathfrak {F}$
:
The diversity of a class of relational frames
![]() $\mathsf {C}$
, written
$\mathsf {C}$
, written
![]() $\Delta (\mathsf {C})$
, is the supremum of diversities of point-generated subframes of frames in
$\Delta (\mathsf {C})$
, is the supremum of diversities of point-generated subframes of frames in
![]() $\mathsf {C}$
, if there is such a cardinal, and undefined otherwise.
$\mathsf {C}$
, if there is such a cardinal, and undefined otherwise.
Below, we will show that for any class
![]() $\mathsf {C}$
of frames which is defined by a finite set of propositionally quantified modal formulas and which has finite diversity,
$\mathsf {C}$
of frames which is defined by a finite set of propositionally quantified modal formulas and which has finite diversity,
![]() $\mathcal {L}(\mathsf {C})$
is decidable; see Theorem 3.13. From this, many new results about the decidability of propositionally quantified modal logics can be derived, and we present a number of examples in Section 3.5.
$\mathcal {L}(\mathsf {C})$
is decidable; see Theorem 3.13. From this, many new results about the decidability of propositionally quantified modal logics can be derived, and we present a number of examples in Section 3.5.
In the following, we will introduce a generalization of the notion of a duplicate, and consider equivalence relations which are refinements of the duplicate relation, i.e., which only relate duplicates. While not strictly necessary, it is worth noting that for the simple notion of duplicates stated in Definition 3.3, there is a very natural alternative characterization of such equivalence relations. We discuss this in the remainder of this section; readers may skip ahead to Section 3.3 without loss of continuity.
Below, we will limit the number of worlds in a frame by reducing the number of duplicates of any world to a certain finite number. This is most straightforwardly done by choosing a suitable subframe, simply omitting any extraneous duplicates. But in the present simple case, an alternative approach is possible: instead of identifying a subset of the set of worlds, and considering the relevant subframe, we can also identify a suitable equivalence relation which is a refinement (subset) of the relation of being a duplicate, and consider the corresponding quotient frame, whose worlds are the equivalence relations of the original frame. The accessibility relations are lifted from the individual worlds to the equivalence classes. For it to be possible to define this lift in a suitable way, one might suppose that the equivalence relation must be a congruence with respect to the accessibility relations. But a weaker requirement suffices. Consider the case of an equivalence relation on a unimodal frame in which all worlds can access themselves but no other worlds. If the equivalence relation is not identity, it is not a congruence. But it is still clear how to define the quotient frame: every equivalence class should be able to access itself, and nothing else. What is needed for it to be possible to define the quotient frame is what we will call a weak congruence, which imposes the usual congruence constraint only on two pairs of equivalent worlds if their first coordinates are identical iff their second coordinates are identical. For such weak congruences, the accessibility relation of the quotient frame is defined as usual, except that an equivalence class can access itself just in case each/one of its members can access itself.
Definition 3.4. Let
![]() $\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
be a relational frame and
$\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
be a relational frame and
![]() $\sim $
an equivalence relation on W.
$\sim $
an equivalence relation on W.
![]() $\sim $
is a weak congruence on
$\sim $
is a weak congruence on
![]() $\mathfrak {F}$
if for all
$\mathfrak {F}$
if for all
![]() $w\sim w',v\sim v'\in W$
and
$w\sim w',v\sim v'\in W$
and
![]() $\Box \in O$
,
$\Box \in O$
,
-
if
 $w=v$
iff
$w=v$
iff
 $w'=v'$
, then
$w'=v'$
, then
 $wR_{\Box } v$
iff
$wR_{\Box } v$
iff
 $w'R_{\Box } v'$
.
$w'R_{\Box } v'$
.
In this case,
![]() $\mathfrak {F}/{\sim }$
is the relational frame
$\mathfrak {F}/{\sim }$
is the relational frame
![]() $\langle W/{\sim },R_{\Box }/{\sim }\rangle _{\Box \in O}$
where
$\langle W/{\sim },R_{\Box }/{\sim }\rangle _{\Box \in O}$
where
-
 $[w]_{\sim } R_{\Box }/{\sim }[v]_{\sim }$
iff
$[w]_{\sim } R_{\Box }/{\sim }[v]_{\sim }$
iff
 $w\nsim v$
and
$w\nsim v$
and
 $wR_{\Box } v$
, or
$wR_{\Box } v$
, or
 $w\sim v$
and
$w\sim v$
and
 $wR_{\Box } w$
.
$wR_{\Box } w$
.
It is routine to show that the constraints on weak congruences suffice to ensure that
![]() $\mathfrak {F}/{\sim }$
is well-defined. It is also easy to verify that an equivalence relation is a weak congruence just in case it relates only duplicates; i.e.,
$\mathfrak {F}/{\sim }$
is well-defined. It is also easy to verify that an equivalence relation is a weak congruence just in case it relates only duplicates; i.e.,
![]() $\sim $
is a weak congruence on
$\sim $
is a weak congruence on
![]() $\mathfrak {F}$
just in case it is a refinement of
$\mathfrak {F}$
just in case it is a refinement of
![]() $\triangle _{\mathfrak {F}}$
. Finally, it can be shown that the result of reducing the worlds of any duplicate class in
$\triangle _{\mathfrak {F}}$
. Finally, it can be shown that the result of reducing the worlds of any duplicate class in
![]() $\mathfrak {F}$
to n members, which we will define in Definition 3.10 as
$\mathfrak {F}$
to n members, which we will define in Definition 3.10 as
![]() $\mathfrak {F}_{\mathrm {id}}^n$
, is isomorphic to the quotient frame
$\mathfrak {F}_{\mathrm {id}}^n$
, is isomorphic to the quotient frame
![]() $\mathfrak {F}/{\sim }$
, where
$\mathfrak {F}/{\sim }$
, where
![]() $\sim $
is any weak congruence which divides every duplicate class d of
$\sim $
is any weak congruence which divides every duplicate class d of
![]() $\mathfrak {F}$
into
$\mathfrak {F}$
into
![]() $\mathrm {min}(|d|,n)$
equivalence classes.
$\mathrm {min}(|d|,n)$
equivalence classes.
3.3 Back and forth systems
This section introduces back and forth systems for
![]() $\mathcal {N}^O$
. Such systems have been developed for a wide range of logics, including propositional modal logic (see the notion of bisimulation in [Reference Blackburn, de Rijke and Venema4, Section 2.2]), first-order logic ([Reference Karp, Addison, Henkin and Tarski29] and [Reference Hodges22, Section 3.2]), second-order logic [Reference Väänänen and Zalta56, Section 3.1], and various quantified modal logics [Reference van Benthem3, p. 123] and [Reference Fritz14] including higher-order and/or infinitary quantified modal logics [Reference Fritz15, Reference Fritz and Goodman17].
$\mathcal {N}^O$
. Such systems have been developed for a wide range of logics, including propositional modal logic (see the notion of bisimulation in [Reference Blackburn, de Rijke and Venema4, Section 2.2]), first-order logic ([Reference Karp, Addison, Henkin and Tarski29] and [Reference Hodges22, Section 3.2]), second-order logic [Reference Väänänen and Zalta56, Section 3.1], and various quantified modal logics [Reference van Benthem3, p. 123] and [Reference Fritz14] including higher-order and/or infinitary quantified modal logics [Reference Fritz15, Reference Fritz and Goodman17].
Definition 3.5. Let
![]() $\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
and
$\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
and
![]() $\mathfrak {F}'=\langle W',R^{\prime }_{\Box }\rangle ^{}_{\Box \in O}$
be relational frames.
$\mathfrak {F}'=\langle W',R^{\prime }_{\Box }\rangle ^{}_{\Box \in O}$
be relational frames.
A partial isomorphism from
![]() $\mathfrak {F}$
to
$\mathfrak {F}$
to
![]() $\mathfrak {F}'$
is a partial injection i from
$\mathfrak {F}'$
is a partial injection i from
![]() $\mathcal {P}(W)$
to
$\mathcal {P}(W)$
to
![]() $\mathcal {P}(W')$
such that for all
$\mathcal {P}(W')$
such that for all
![]() $x,y\in \mathrm {dom}(i)$
and
$x,y\in \mathrm {dom}(i)$
and
![]() $\Box \in O$
:
$\Box \in O$
:
-
•
 $x\subseteq y$
iff
$x\subseteq y$
iff
 $i(x)\subseteq i(y)$
, and
$i(x)\subseteq i(y)$
, and -
• for all
 $w\in x$
there is a
$w\in x$
there is a
 $v\in y$
such that
$v\in y$
such that
 $wR_{\Box } v$
iff for all
$wR_{\Box } v$
iff for all
 $w'\in i(x)$
there is a
$w'\in i(x)$
there is a
 $v'\in i(y)$
such that
$v'\in i(y)$
such that
 $w'R^{\prime }_{\Box } v'$
.
$w'R^{\prime }_{\Box } v'$
.
A back and forth system from
![]() $\mathfrak {F}$
to
$\mathfrak {F}$
to
![]() $\mathfrak {F}'$
is a function I mapping every
$\mathfrak {F}'$
is a function I mapping every
![]() $n\in \mathbb {N}$
to a set of partial isomorphisms, such that for all
$n\in \mathbb {N}$
to a set of partial isomorphisms, such that for all
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $i\in I_{n+1}$
:
$i\in I_{n+1}$
:
-
• for all
 $x\subseteq W$
, there is a
$x\subseteq W$
, there is a
 $j\supseteq i$
in
$j\supseteq i$
in
 $I_n$
such that
$I_n$
such that
 $x\in \mathrm {dom}(j)$
, and
$x\in \mathrm {dom}(j)$
, and -
• for all
 $x'\subseteq W'$
, there is a
$x'\subseteq W'$
, there is a
 $j\supseteq i$
in
$j\supseteq i$
in
 $I_n$
such that
$I_n$
such that
 $x'\in \mathrm {im}(j)$
.
$x'\in \mathrm {im}(j)$
.
![]() $I_n$
is the nth stage of I.
$I_n$
is the nth stage of I.
This definition is set up just to allow for the following result, which shows that worlds of two frames connected by a partial isomorphism in the nth stage of a back and forth system validate the same formulas up to quantifier depth n, relative to suitable assignment functions:
Proposition 3.6. Let
![]() $\mathfrak {F}$
and
$\mathfrak {F}$
and
![]() $\mathfrak {F}'$
be relational frames, I a back and forth system from
$\mathfrak {F}'$
be relational frames, I a back and forth system from
![]() $\mathfrak {F}$
to
$\mathfrak {F}$
to
![]() $\mathfrak {F}'$
,
$\mathfrak {F}'$
,
![]() $\varphi \in \mathcal {N}^O$
,
$\varphi \in \mathcal {N}^O$
,
![]() $n\geq \mathrm {qd}(\varphi )$
,
$n\geq \mathrm {qd}(\varphi )$
,
![]() $i\in I_n$
, and a an assignment function for
$i\in I_n$
, and a an assignment function for
![]() $\mathfrak {F}$
such that
$\mathfrak {F}$
such that
![]() $\mathrm {im}(a)\subseteq \mathrm {dom}(i)$
. Then,
$\mathrm {im}(a)\subseteq \mathrm {dom}(i)$
. Then,
Proof By induction on the complexity of
![]() $\varphi $
.
$\varphi $
.
Using the notion of n-equivalence, we can sum up to the consequences of this lemma for closed formulas more concisely as follows:
Corollary 3.7. If
![]() $\mathfrak {F}$
and
$\mathfrak {F}$
and
![]() $\mathfrak {F}'$
are relational frames, I is a back and forth system from
$\mathfrak {F}'$
are relational frames, I is a back and forth system from
![]() $\mathfrak {F}$
to
$\mathfrak {F}$
to
![]() $\mathfrak {F}'$
,
$\mathfrak {F}'$
,
![]() $n\geq \mathrm {qd}(\varphi )$
, and
$n\geq \mathrm {qd}(\varphi )$
, and
![]() $I_n$
is non-empty, then
$I_n$
is non-empty, then
![]() $\mathfrak {F}$
and
$\mathfrak {F}$
and
![]() $\mathfrak {F}'$
are n-equivalent.
$\mathfrak {F}'$
are n-equivalent.
3.4 Reducing frames
We will now use back and forth systems to show that for any relational frame, an n-equivalent subframe can be obtained by limiting the number of duplicates of any given world to
![]() $2^n$
. However, for applications in the multimodal case in Section 6.2, it will be useful to develop this idea in a more general form.
$2^n$
. However, for applications in the multimodal case in Section 6.2, it will be useful to develop this idea in a more general form.
The simplest multimodal application which motivates this generalization is the case of bimodal frames in which both accessibility relations are equivalence relations, one of which is a refinement (subset) of the other. Let these relations be
![]() $R_{\boxtimes }\subseteq R_{\Box }$
. In a point-generated subframe of such a frame,
$R_{\boxtimes }\subseteq R_{\Box }$
. In a point-generated subframe of such a frame,
![]() $R_{\Box }$
is the universal relation. Any members of an
$R_{\Box }$
is the universal relation. Any members of an
![]() $R_{\boxtimes }$
-equivalence class are therefore duplicates. By reducing the number of duplicate worlds, these equivalence classes can therefore be shrunk to a size no greater than
$R_{\boxtimes }$
-equivalence class are therefore duplicates. By reducing the number of duplicate worlds, these equivalence classes can therefore be shrunk to a size no greater than
![]() $2^n$
, while retaining an n-equivalent subframe. The resulting subframe may still be infinite, since there may still be infinitely many
$2^n$
, while retaining an n-equivalent subframe. The resulting subframe may still be infinite, since there may still be infinitely many
![]() $R_{\boxtimes }$
-equivalence classes. However, the size of these equivalence classes is bounded by
$R_{\boxtimes }$
-equivalence classes. However, the size of these equivalence classes is bounded by
![]() $2^n$
, and there is no way of distinguishing two equivalence classes structurally other than in terms of their size. We can therefore apply the idea of reducing numbers of duplicates again, but on the level of equivalence classes of worlds instead of the worlds themselves, by reducing the duplicates of any
$2^n$
, and there is no way of distinguishing two equivalence classes structurally other than in terms of their size. We can therefore apply the idea of reducing numbers of duplicates again, but on the level of equivalence classes of worlds instead of the worlds themselves, by reducing the duplicates of any
![]() $R_{\boxtimes }$
-equivalence class to a finite number. It turns out that we can obtain an n-equivalent subframe by limiting the number of duplicates of
$R_{\boxtimes }$
-equivalence class to a finite number. It turns out that we can obtain an n-equivalent subframe by limiting the number of duplicates of
![]() $R_{\boxtimes }$
-equivalence classes to
$R_{\boxtimes }$
-equivalence classes to
![]() $2^{2^nn}$
.
$2^{2^nn}$
.
In anticipation of this generalization, we first generalize the notion of a duplicate from worlds to equivalence classes of worlds, relative to an arbitrary equivalence relation. It will also be useful to relativize the notion of a duplicate in a frame to a finite sequence of sets of worlds, which are understood as imposing additional structure on the frame under consideration. These sets of worlds will later be used to account for free variables, when considering open formulas. We therefore introduce the notion of an augmented frame, which adds to a relational frame
![]() $\mathfrak {F}$
an equivalence relation
$\mathfrak {F}$
an equivalence relation
![]() $\sim $
and a finite sequence of sets of worlds
$\sim $
and a finite sequence of sets of worlds
![]() $\alpha $
, and define what it takes for equivalence classes x and y to be duplicates in such an augmented frame: there must be an isomorphism between the subframes based on x and y, and this isomorphism must constitute an automorphism of the whole frame. Here, the notion of a subframe of an augmented frame is defined in the obvious way:
$\alpha $
, and define what it takes for equivalence classes x and y to be duplicates in such an augmented frame: there must be an isomorphism between the subframes based on x and y, and this isomorphism must constitute an automorphism of the whole frame. Here, the notion of a subframe of an augmented frame is defined in the obvious way:
![]() $\langle \mathfrak {F},{\sim },\alpha \rangle |x$
is
$\langle \mathfrak {F},{\sim },\alpha \rangle |x$
is
![]() $\langle \mathfrak {F}|x,{\sim }\cap x^2,\alpha '\rangle $
, where
$\langle \mathfrak {F}|x,{\sim }\cap x^2,\alpha '\rangle $
, where
![]() $\alpha '(m)=\alpha (m)\cap x$
for all
$\alpha '(m)=\alpha (m)\cap x$
for all
![]() $m\in \mathrm {dom}(\alpha )$
.
$m\in \mathrm {dom}(\alpha )$
.
Definition 3.8. An augmented frame is a structure
![]() $\mathfrak {A}=\langle \mathfrak {F},{\sim },\alpha \rangle $
, where
$\mathfrak {A}=\langle \mathfrak {F},{\sim },\alpha \rangle $
, where
![]() $\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
is a relational frame,
$\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
is a relational frame,
![]() $\sim $
is an equivalence relation on W, and
$\sim $
is an equivalence relation on W, and
![]() $\alpha $
is a sequence of pairwise distinct elements of
$\alpha $
is a sequence of pairwise distinct elements of
![]() $\mathcal {P}(W)$
of some finite length
$\mathcal {P}(W)$
of some finite length
![]() $k\in \mathbb {N}$
.
$k\in \mathbb {N}$
.
![]() $x,y\in W/{\sim }$
are duplicates in
$x,y\in W/{\sim }$
are duplicates in
![]() $\mathfrak {A}$
if there is an isomorphism f from
$\mathfrak {A}$
if there is an isomorphism f from
![]() $\mathfrak {A}|x$
to
$\mathfrak {A}|x$
to
![]() $\mathfrak {A}|y$
, and
$\mathfrak {A}|y$
, and
![]() $\hat {f}$
is an automorphism of
$\hat {f}$
is an automorphism of
![]() $\mathfrak {A}$
, where
$\mathfrak {A}$
, where
![]() $\hat {f}$
is the function on W such that for all
$\hat {f}$
is the function on W such that for all
![]() $w\in W$
,
$w\in W$
,
 $$\begin{align*}\hat{f}(w)=\begin{cases} f(w), & \text{if } w\in x, \\ f^{-1}(w), & \text{if } w\in y, \\ w, & \text{otherwise.} \end{cases}\end{align*}$$
$$\begin{align*}\hat{f}(w)=\begin{cases} f(w), & \text{if } w\in x, \\ f^{-1}(w), & \text{if } w\in y, \\ w, & \text{otherwise.} \end{cases}\end{align*}$$
![]() $\triangle _{\mathfrak {A}}$
is the relation of being a duplicate in
$\triangle _{\mathfrak {A}}$
is the relation of being a duplicate in
![]() $\mathfrak {A}$
. A duplicate congruence on
$\mathfrak {A}$
. A duplicate congruence on
![]() $\mathfrak {A}$
is an equivalence relation on
$\mathfrak {A}$
is an equivalence relation on
![]() $W/{\sim }$
which relates only duplicates in
$W/{\sim }$
which relates only duplicates in
![]() $\mathfrak {A}$
.
$\mathfrak {A}$
.
Since
![]() $\triangle _{\mathfrak {A}}$
is an equivalence relation on
$\triangle _{\mathfrak {A}}$
is an equivalence relation on
![]() $W/{\sim }$
, it is the coarsest duplicate congruence on
$W/{\sim }$
, it is the coarsest duplicate congruence on
![]() $\mathfrak {A}$
. It is also easy to see that the original notion of duplicate worlds in a relational frame
$\mathfrak {A}$
. It is also easy to see that the original notion of duplicate worlds in a relational frame
![]() $\mathfrak {F}$
can be recovered from the notion of duplicate equivalence classes by augmenting
$\mathfrak {F}$
can be recovered from the notion of duplicate equivalence classes by augmenting
![]() $\mathfrak {F}$
with the equivalence relation
$\mathfrak {F}$
with the equivalence relation
![]() $\mathrm {id}$
of identity and the empty sequence
$\mathrm {id}$
of identity and the empty sequence
![]() $\langle \rangle $
, and considering any world to be represented by its singleton set:
$\langle \rangle $
, and considering any world to be represented by its singleton set:
![]() $w\triangle _{\mathfrak {F}}v$
is equivalent to
$w\triangle _{\mathfrak {F}}v$
is equivalent to
![]() $\{w\}\triangle _{\langle \mathfrak {F},\mathrm {id},\langle \rangle \rangle }\{v\}$
.
$\{w\}\triangle _{\langle \mathfrak {F},\mathrm {id},\langle \rangle \rangle }\{v\}$
.
We can now define the notion of a subframe obtained by reducing the number of duplicate equivalence classes to n: We first index duplicate equivalence classes by ordinals, and then take the subframe based on those worlds which are in equivalence classes with index
![]() $<n$
. Strictly speaking, the resulting subframe will be depended on the choice of the indexing function, but as such subframes are unique up to isomorphism, we can ignore this dependence.
$<n$
. Strictly speaking, the resulting subframe will be depended on the choice of the indexing function, but as such subframes are unique up to isomorphism, we can ignore this dependence.
Definition 3.9. Assume
![]() $\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
is a relational frame,
$\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
is a relational frame,
![]() $\sim $
an equivalence relation on W, and
$\sim $
an equivalence relation on W, and
![]() $n>0$
. Let
$n>0$
. Let
![]() $\mathfrak {A}=\langle \mathfrak {F},{\sim },\langle \rangle \rangle $
. Consider any function
$\mathfrak {A}=\langle \mathfrak {F},{\sim },\langle \rangle \rangle $
. Consider any function
![]() $\delta $
mapping every
$\delta $
mapping every
![]() $x\in W/{\sim }$
to an ordinal
$x\in W/{\sim }$
to an ordinal
![]() $\delta (x)$
such that for every duplicate class
$\delta (x)$
such that for every duplicate class
![]() $D\in W/{\sim }/\triangle _{\mathfrak {A}}$
,
$D\in W/{\sim }/\triangle _{\mathfrak {A}}$
,
![]() $\delta |D$
is a bijection from D to
$\delta |D$
is a bijection from D to
![]() $|D|$
.
$|D|$
.
![]() $\mathfrak {F}^n_{\sim }$
is the subframe of
$\mathfrak {F}^n_{\sim }$
is the subframe of
![]() $\mathfrak {F}$
based on the set
$\mathfrak {F}$
based on the set
![]() $W'$
such that
$W'$
such that
![]() $w\in W'$
iff
$w\in W'$
iff
![]() $\delta ([w]_{\sim })<n$
, for all
$\delta ([w]_{\sim })<n$
, for all
![]() $w\in W$
.
$w\in W$
.
As the next step, we will connect
![]() $\mathfrak {F}$
and
$\mathfrak {F}$
and
![]() $\mathfrak {F}^n_{\sim }$
by a back and forth system. We do so by first defining a way of connecting any two relational frames, with associated equivalence relations, by a generic back and forth system. Of course, if the underlying relational frames are insufficiently similar, then this generic back and forth system will not be very useful, since most of its stages will be empty. The central idea behind the construction of the generic back and forth system is that a partial isomorphism between the relational frames is determined by any bijection f between the equivalence classes of duplicate congruences of the augmented frames satisfying certain additional conditions. Most importantly, if f maps equivalence class x to
$\mathfrak {F}^n_{\sim }$
by a back and forth system. We do so by first defining a way of connecting any two relational frames, with associated equivalence relations, by a generic back and forth system. Of course, if the underlying relational frames are insufficiently similar, then this generic back and forth system will not be very useful, since most of its stages will be empty. The central idea behind the construction of the generic back and forth system is that a partial isomorphism between the relational frames is determined by any bijection f between the equivalence classes of duplicate congruences of the augmented frames satisfying certain additional conditions. Most importantly, if f maps equivalence class x to
![]() $x'$
, then the subframes based on x and
$x'$
, then the subframes based on x and
![]() $x'$
must be isomorphic. Further, if f also maps y to
$x'$
must be isomorphic. Further, if f also maps y to
![]() $y'$
, then corresponding worlds in x and
$y'$
, then corresponding worlds in x and
![]() $x'$
must relate to corresponding worlds in y and
$x'$
must relate to corresponding worlds in y and
![]() $y'$
in corresponding ways in terms of the accessibility relations. Effectively, such a bijection f divides the equivalence classes of worlds of the two frames into clusters of duplicates, with the two frames being alike except that the relevant clusters may contain different numbers of duplicates. These numbers of duplicates will be important, and we call f an n-correspondence if it only connects clusters whose size is either both at least n, or identical. The generic back and forth system can now be defined, by including in its nth stage the partial isomorphisms determined by
$y'$
in corresponding ways in terms of the accessibility relations. Effectively, such a bijection f divides the equivalence classes of worlds of the two frames into clusters of duplicates, with the two frames being alike except that the relevant clusters may contain different numbers of duplicates. These numbers of duplicates will be important, and we call f an n-correspondence if it only connects clusters whose size is either both at least n, or identical. The generic back and forth system can now be defined, by including in its nth stage the partial isomorphisms determined by
![]() $2^{ln}$
-correspondences, where l bounds the sizes of equivalence classes in the augmented frames. Given such a correspondence f, the relevant partial isomorphism can be read off just from the augmented frames connected by f, in particular their third components
$2^{ln}$
-correspondences, where l bounds the sizes of equivalence classes in the augmented frames. Given such a correspondence f, the relevant partial isomorphism can be read off just from the augmented frames connected by f, in particular their third components
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
: the relevant partial isomorphism maps
$\alpha '$
: the relevant partial isomorphism maps
![]() $\alpha (m)$
to
$\alpha (m)$
to
![]() $\alpha '(m)$
, whenever these are defined. We therefore also require these sequences to have the same length, as part of the definition of an n-correspondence.
$\alpha '(m)$
, whenever these are defined. We therefore also require these sequences to have the same length, as part of the definition of an n-correspondence.
Definition 3.10. Let
![]() $\mathfrak {A}=\langle \mathfrak {F},{\sim },\alpha \rangle $
and
$\mathfrak {A}=\langle \mathfrak {F},{\sim },\alpha \rangle $
and
![]() $\mathfrak {A}'=\langle \mathfrak {F}',{\sim '},\alpha '\rangle $
be augmented frames, with
$\mathfrak {A}'=\langle \mathfrak {F}',{\sim '},\alpha '\rangle $
be augmented frames, with
![]() $\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
and
$\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
and
![]() $\mathfrak {F}'=\langle W',R^{\prime }_{\Box }\rangle ^{}_{\Box \in O}$
.
$\mathfrak {F}'=\langle W',R^{\prime }_{\Box }\rangle ^{}_{\Box \in O}$
.
For any
![]() $n>1$
, an n-correspondence from
$n>1$
, an n-correspondence from
![]() $\mathfrak {A}$
to
$\mathfrak {A}$
to
![]() $\mathfrak {A}'$
is a function f satisfying all of the following conditions:
$\mathfrak {A}'$
is a function f satisfying all of the following conditions:
-
(i) f is a bijection from
 $W/{\sim }/{\approx }$
to
$W/{\sim }/{\approx }$
to
 $W'/{\sim '}/{\approx '}$
, where
$W'/{\sim '}/{\approx '}$
, where
 $\approx $
is a duplicate congruence on
$\approx $
is a duplicate congruence on
 $\mathfrak {A}$
and
$\mathfrak {A}$
and
 $\approx '$
is a duplicate congruence on
$\approx '$
is a duplicate congruence on
 $\mathfrak {A}'$
.
$\mathfrak {A}'$
. -
(ii)
 $\alpha $
and
$\alpha $
and
 $\alpha '$
have the same length k.
$\alpha '$
have the same length k. -
(iii) For any
 $x\in W/{\sim }$
and
$x\in W/{\sim }$
and
 $x'\in f([x]_{\approx })$
, there is an isomorphism g from
$x'\in f([x]_{\approx })$
, there is an isomorphism g from
 $\mathfrak {A}|x$
to
$\mathfrak {A}|x$
to
 $\mathfrak {A}'|x'$
.
$\mathfrak {A}'|x'$
. -
(iv) For any
 $x,y\in W/{\sim }$
,
$x,y\in W/{\sim }$
,
 $x'\in f([x]_{\approx })$
,
$x'\in f([x]_{\approx })$
,
 $y'\in f([y]_{\approx })$
, isomorphisms g from
$y'\in f([y]_{\approx })$
, isomorphisms g from
 $\mathfrak {A}|x$
to
$\mathfrak {A}|x$
to
 $\mathfrak {A}'|x'$
and h from
$\mathfrak {A}'|x'$
and h from
 $\mathfrak {A}|y$
to
$\mathfrak {A}|y$
to
 $\mathfrak {A}'|y'$
,
$\mathfrak {A}'|y'$
,
 $w\in x$
,
$w\in x$
,
 $v\in y$
, and
$v\in y$
, and
 $\Box \in O$
:
$\Box \in O$
:  $$\begin{align*}wR_{\Box} v\text{ iff }g(w)R^{\prime}_{\Box} h(v).\end{align*}$$
$$\begin{align*}wR_{\Box} v\text{ iff }g(w)R^{\prime}_{\Box} h(v).\end{align*}$$
-
(v) For all
 $X\in \mathrm {dom}(f)$
, either
$X\in \mathrm {dom}(f)$
, either
 $|X|\geq n$
and
$|X|\geq n$
and
 $|f(X)|\geq n$
, or
$|f(X)|\geq n$
, or
 $|X|=|f(X)|$
.
$|X|=|f(X)|$
.
Assuming
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
have the same length k,
$\alpha '$
have the same length k,
![]() $i_{\mathfrak {A}}^{\mathfrak {A}'}$
is the partial function from
$i_{\mathfrak {A}}^{\mathfrak {A}'}$
is the partial function from
![]() $\mathcal {P}(W)$
to
$\mathcal {P}(W)$
to
![]() $\mathcal {P}(W')$
such that
$\mathcal {P}(W')$
such that
-
 $i_{\mathfrak {A}}^{\mathfrak {A}'}(x)=x'$
whenever
$i_{\mathfrak {A}}^{\mathfrak {A}'}(x)=x'$
whenever
 $x=\alpha (m)$
and
$x=\alpha (m)$
and
 $x'=\alpha '(m)$
, for some
$x'=\alpha '(m)$
, for some
 $m\leq k$
.
$m\leq k$
.
Given relational frames
![]() $\mathfrak {F}$
and
$\mathfrak {F}$
and
![]() $\mathfrak {F}'$
, equivalence relations
$\mathfrak {F}'$
, equivalence relations
![]() $\sim $
and
$\sim $
and
![]() $\sim '$
, and
$\sim '$
, and
![]() $n\in \mathbb {N}$
, let
$n\in \mathbb {N}$
, let
![]() $I_n$
be the set of functions
$I_n$
be the set of functions
![]() $i_{\mathfrak {A}}^{\mathfrak {A}'}$
for
$i_{\mathfrak {A}}^{\mathfrak {A}'}$
for
![]() $\mathfrak {A}$
an augmented frame based on
$\mathfrak {A}$
an augmented frame based on
![]() $\mathfrak {F}$
and
$\mathfrak {F}$
and
![]() $\sim $
and
$\sim $
and
![]() $\mathfrak {A}'$
an augmented frame based on
$\mathfrak {A}'$
an augmented frame based on
![]() $\mathfrak {F}'$
and
$\mathfrak {F}'$
and
![]() $\sim '$
such that there exists a
$\sim '$
such that there exists a
![]() $2^{ln}$
-correspondence from
$2^{ln}$
-correspondence from
![]() $\mathfrak {A}$
to
$\mathfrak {A}$
to
![]() $\mathfrak {A}'$
, where
$\mathfrak {A}'$
, where
![]() $l=\mathrm {sup}\{|x|:x\in W/{\sim }\}$
.
$l=\mathrm {sup}\{|x|:x\in W/{\sim }\}$
.
![]() $I_{\mathfrak {F},{\sim }}^{\mathfrak {F}',{\sim '}}$
is the function mapping any
$I_{\mathfrak {F},{\sim }}^{\mathfrak {F}',{\sim '}}$
is the function mapping any
![]() $n\in \mathbb {N}$
to
$n\in \mathbb {N}$
to
![]() $I_n$
.
$I_n$
.
The next lemma shows that this construction succeeds, at least insofar as
![]() $I_{\mathfrak {F},{\sim }}^{\mathfrak {F}',{\sim '}}$
is indeed a back and forth system. Note that it is immediate by construction that if
$I_{\mathfrak {F},{\sim }}^{\mathfrak {F}',{\sim '}}$
is indeed a back and forth system. Note that it is immediate by construction that if
![]() $m\leq n$
, then
$m\leq n$
, then
![]() $I_m\supseteq I_n$
. In the proof, we write
$I_m\supseteq I_n$
. In the proof, we write
![]() $\alpha ^{\smallfrown } x$
for the result of appending x to the end of a sequence
$\alpha ^{\smallfrown } x$
for the result of appending x to the end of a sequence
![]() $\alpha $
.
$\alpha $
.
Lemma 3.11. For any relational frames
![]() $\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
and
$\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
and
![]() $\mathfrak {F}'=\langle W',R^{\prime }_{\Box }\rangle ^{}_{\Box \in O}$
and equivalence relations
$\mathfrak {F}'=\langle W',R^{\prime }_{\Box }\rangle ^{}_{\Box \in O}$
and equivalence relations
![]() $\sim $
and
$\sim $
and
![]() ${\sim '}$
on W and
${\sim '}$
on W and
![]() $W'$
, respectively,
$W'$
, respectively,
![]() $I_{\mathfrak {F},{\sim }}^{\mathfrak {F}',{\sim '}}$
is a back and forth system from
$I_{\mathfrak {F},{\sim }}^{\mathfrak {F}',{\sim '}}$
is a back and forth system from
![]() $\mathfrak {F}$
to
$\mathfrak {F}$
to
![]() $\mathfrak {F}'$
.
$\mathfrak {F}'$
.
Proof It is routine to show that for every
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $I_n$
is a set of partial isomorphisms. So consider any
$I_n$
is a set of partial isomorphisms. So consider any
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $i\in I_{n+1}$
. By symmetry, it suffices to consider only the first condition. So, let
$i\in I_{n+1}$
. By symmetry, it suffices to consider only the first condition. So, let
![]() $x\subseteq W$
. If
$x\subseteq W$
. If
![]() $x\in \mathrm {dom}(i)$
, the claim is immediate, so assume otherwise.
$x\in \mathrm {dom}(i)$
, the claim is immediate, so assume otherwise.
Let
![]() $\mathfrak {A}=\langle \mathfrak {F},{\sim },\alpha \rangle $
and
$\mathfrak {A}=\langle \mathfrak {F},{\sim },\alpha \rangle $
and
![]() $\mathfrak {A}'=\langle \mathfrak {F}',{\sim '},\alpha '\rangle $
be augmented frames determining i, and f be the required
$\mathfrak {A}'=\langle \mathfrak {F}',{\sim '},\alpha '\rangle $
be augmented frames determining i, and f be the required
![]() $2^{l(n+1)}$
-correspondence, where
$2^{l(n+1)}$
-correspondence, where
![]() $l=\mathrm {sup}\{|s|:s\in W/{\sim }\}$
. Consequently, f is a bijection from
$l=\mathrm {sup}\{|s|:s\in W/{\sim }\}$
. Consequently, f is a bijection from
![]() $W/{\sim }/{\approx }$
to
$W/{\sim }/{\approx }$
to
![]() $W'/{\sim '}/{\approx '}$
, where
$W'/{\sim '}/{\approx '}$
, where
![]() $\approx $
is a duplicate congruence on
$\approx $
is a duplicate congruence on
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\approx '$
is duplicate congruence on
$\approx '$
is duplicate congruence on
![]() $\mathfrak {A}'$
. Let
$\mathfrak {A}'$
. Let
![]() $\overline {\mathfrak {A}}=\langle \mathfrak {F},{\sim },\alpha ^{\smallfrown } x\rangle $
, and
$\overline {\mathfrak {A}}=\langle \mathfrak {F},{\sim },\alpha ^{\smallfrown } x\rangle $
, and
![]() $\overline {\approx }$
the refinement of
$\overline {\approx }$
the refinement of
![]() $\approx $
which relates
$\approx $
which relates
![]() $y\approx z$
just in case y and z are duplicates in
$y\approx z$
just in case y and z are duplicates in
![]() $\overline {\mathfrak {A}}$
. Note that
$\overline {\mathfrak {A}}$
. Note that
![]() $\overline {\approx }$
divides every equivalence class of
$\overline {\approx }$
divides every equivalence class of
![]() $\approx $
into at most
$\approx $
into at most
![]() $2^l$
classes. So, for cardinality reasons, there is a refinement
$2^l$
classes. So, for cardinality reasons, there is a refinement
![]() $\overline {\approx }'$
of
$\overline {\approx }'$
of
![]() $\approx '$
and bijection g from
$\approx '$
and bijection g from
![]() $W/{\sim }/{\overline {\approx }}$
to
$W/{\sim }/{\overline {\approx }}$
to
![]() $W'/{\sim '}/{\overline {\approx }'}$
which refines f in the sense that if
$W'/{\sim '}/{\overline {\approx }'}$
which refines f in the sense that if
![]() $g([y]_{\overline {\approx }})=[y']_{\overline {\approx }'}$
then
$g([y]_{\overline {\approx }})=[y']_{\overline {\approx }'}$
then
![]() $f([y]_{\approx })=[y']_{\approx '}$
, such that for every
$f([y]_{\approx })=[y']_{\approx '}$
, such that for every
![]() $X\in W/{\sim }/{\overline {\approx }}$
, either
$X\in W/{\sim }/{\overline {\approx }}$
, either
![]() $|X|\geq 2^{ln}$
and
$|X|\geq 2^{ln}$
and
![]() $|g(X)|\geq 2^{ln}$
, or
$|g(X)|\geq 2^{ln}$
, or
![]() $|X|=|g(X)|$
.
$|X|=|g(X)|$
.
For every
![]() $X'\in W/{\sim '}/{\overline {\approx }'}$
, choose some representative
$X'\in W/{\sim '}/{\overline {\approx }'}$
, choose some representative
![]() $r_{X'}\in X'$
,
$r_{X'}\in X'$
,
![]() $y_{X'}\in g^{-1}(X')$
, and isomorphism
$y_{X'}\in g^{-1}(X')$
, and isomorphism
![]() $h_{X'}$
from
$h_{X'}$
from
![]() $\mathfrak {A}'|r_{X'}$
to
$\mathfrak {A}'|r_{X'}$
to
![]() $\mathfrak {A}|y_{X'}$
. For every
$\mathfrak {A}|y_{X'}$
. For every
![]() $y'\in W/{\sim '}$
, choose some isomorphism
$y'\in W/{\sim '}$
, choose some isomorphism
![]() $h_{y'}$
witnessing that
$h_{y'}$
witnessing that
![]() $y'$
and
$y'$
and
![]() $r_{[y']_{\overline {\approx }'}}$
are duplicates in
$r_{[y']_{\overline {\approx }'}}$
are duplicates in
![]() $\mathfrak {A}'$
. Define
$\mathfrak {A}'$
. Define
![]() $y^{\prime }_x=\{w'\in y':h_{[y']_{\overline {\approx }'}}\circ h_{y'}(w')\in x\}$
. Let
$y^{\prime }_x=\{w'\in y':h_{[y']_{\overline {\approx }'}}\circ h_{y'}(w')\in x\}$
. Let
![]() $x'=\bigcup \{y^{\prime }_x:y'\in W'/{\sim '}\}$
and
$x'=\bigcup \{y^{\prime }_x:y'\in W'/{\sim '}\}$
and
![]() $\overline {\mathfrak {A}}'=\langle \mathfrak {F}',{\sim '},\alpha ^{\prime \smallfrown } x'\rangle $
. Since x is not among the sets indexed by
$\overline {\mathfrak {A}}'=\langle \mathfrak {F}',{\sim '},\alpha ^{\prime \smallfrown } x'\rangle $
. Since x is not among the sets indexed by
![]() $\alpha $
, it follows by the construction that
$\alpha $
, it follows by the construction that
![]() $x'$
is not among the sets indexed by
$x'$
is not among the sets indexed by
![]() $\alpha '$
, so
$\alpha '$
, so
![]() $\overline {\mathfrak {A}}'$
is an augmented frame. It is routine to verify that g is a
$\overline {\mathfrak {A}}'$
is an augmented frame. It is routine to verify that g is a
![]() $2^{ln}$
-correspondence from
$2^{ln}$
-correspondence from
![]() $\overline {\mathfrak {A}}$
to
$\overline {\mathfrak {A}}$
to
![]() $\overline {\mathfrak {A}}'$
. From this, it follows that
$\overline {\mathfrak {A}}'$
. From this, it follows that
![]() $j:=i_{\overline {\mathfrak {A}}}^{\overline {\mathfrak {A}}'}\in I_n$
. It is also clear that
$j:=i_{\overline {\mathfrak {A}}}^{\overline {\mathfrak {A}}'}\in I_n$
. It is also clear that
![]() $j\supseteq i$
and
$j\supseteq i$
and
![]() $x\in \mathrm {dom}(j)$
, as required.
$x\in \mathrm {dom}(j)$
, as required.
We are now ready to put together the pieces developed in this section:
![]() $\mathfrak {F}^m_{\sim }$
is obtained from
$\mathfrak {F}^m_{\sim }$
is obtained from
![]() $\mathfrak {F}$
by reducing the number of duplicate equivalence classes to at most m. Letting
$\mathfrak {F}$
by reducing the number of duplicate equivalence classes to at most m. Letting
![]() $\approx $
be the duplicate relation, and
$\approx $
be the duplicate relation, and
![]() $\approx '$
its restriction for
$\approx '$
its restriction for
![]() $\mathfrak {F}^m_{\sim }$
, there is a straightforward m-correspondence, mapping every duplicate cluster to its reduction. We have seen that the corresponding partial isomorphism is contained in a stage of the generic back and forth system, the index of which is determined by m and the limit of the sizes of
$\mathfrak {F}^m_{\sim }$
, there is a straightforward m-correspondence, mapping every duplicate cluster to its reduction. We have seen that the corresponding partial isomorphism is contained in a stage of the generic back and forth system, the index of which is determined by m and the limit of the sizes of
![]() $\sim $
-equivalence classes. From this, it follows that
$\sim $
-equivalence classes. From this, it follows that
![]() $\mathfrak {F}$
and
$\mathfrak {F}$
and
![]() $\mathfrak {F}^m_{\sim }$
satisfy the same closed formulas up to a certain complexity.
$\mathfrak {F}^m_{\sim }$
satisfy the same closed formulas up to a certain complexity.
Proposition 3.12. Assume
![]() $\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
is a relational frame,
$\mathfrak {F}=\langle W,R_{\Box }\rangle _{\Box \in O}$
is a relational frame,
![]() $\sim $
an equivalence relation on W, and
$\sim $
an equivalence relation on W, and
![]() $n\in \mathbb {N}$
. Let
$n\in \mathbb {N}$
. Let
![]() $l=\mathrm {sup}\{|x|:x\in W/{\sim }\}$
. Then
$l=\mathrm {sup}\{|x|:x\in W/{\sim }\}$
. Then
![]() $\mathfrak {F}$
and
$\mathfrak {F}$
and
![]() $\mathfrak {F}^{2^{ln}}_{\sim }$
are n-equivalent.
$\mathfrak {F}^{2^{ln}}_{\sim }$
are n-equivalent.
Proof Let
![]() $\mathfrak {F}'=\mathfrak {F}^{2^{ln}}_{\sim }$
,
$\mathfrak {F}'=\mathfrak {F}^{2^{ln}}_{\sim }$
,
![]() $W'$
the set of worlds of
$W'$
the set of worlds of
![]() $\mathfrak {F}'$
, and
$\mathfrak {F}'$
, and
![]() ${\sim '}={\sim }|W'$
. Let
${\sim '}={\sim }|W'$
. Let
![]() $\mathfrak {A}=\langle \mathfrak {F},{\sim },\langle \rangle \rangle $
,
$\mathfrak {A}=\langle \mathfrak {F},{\sim },\langle \rangle \rangle $
,
![]() $\mathfrak {A}'=\langle \mathfrak {F}',{\sim '},\langle \rangle \rangle $
,
$\mathfrak {A}'=\langle \mathfrak {F}',{\sim '},\langle \rangle \rangle $
,
![]() ${\approx }=\triangle _{\mathfrak {A}}$
, and
${\approx }=\triangle _{\mathfrak {A}}$
, and
![]() ${\approx '}={\approx }|(W'/{\sim '})$
. Let f be the function from
${\approx '}={\approx }|(W'/{\sim '})$
. Let f be the function from
![]() $W/{\sim }/{\approx }$
to
$W/{\sim }/{\approx }$
to
![]() $W'/{\sim '}/{\approx '}$
such that
$W'/{\sim '}/{\approx '}$
such that
![]() $f:X\mapsto X|(W'/{\sim '})$
. Then f is a
$f:X\mapsto X|(W'/{\sim '})$
. Then f is a
![]() $2^{ln}$
-correspondence from
$2^{ln}$
-correspondence from
![]() $\mathfrak {A}$
to
$\mathfrak {A}$
to
![]() $\mathfrak {A}'$
. So
$\mathfrak {A}'$
. So
![]() $i_{\mathfrak {A}}^{\mathfrak {A}'}$
is a member of the nth stage of
$i_{\mathfrak {A}}^{\mathfrak {A}'}$
is a member of the nth stage of
![]() $I_{\mathfrak {F},{\sim }}^{\mathfrak {F}',{\sim '}}$
. By Lemma 3.11 and Corollary 3.7, it follows that
$I_{\mathfrak {F},{\sim }}^{\mathfrak {F}',{\sim '}}$
. By Lemma 3.11 and Corollary 3.7, it follows that
![]() $\mathfrak {F}$
and
$\mathfrak {F}$
and
![]() $\mathfrak {F}'$
are n-equivalent.
$\mathfrak {F}'$
are n-equivalent.
3.5 Decidability via finite diversity
In this section, we turn to the first application of reducing frames, and prove the decidability of several unimodal logics. First, we show generally that any class of relational frames defined by a finite set of formulas which has finite diversity gives rise to a decidable propositionally quantified modal logic. For this relatively simple result, much of the complexity involved above can be ignored, as we may work just with reductions in which the equivalence relation on worlds is identity. Using Proposition 3.12, we can thus note that any frame of diversity n can be reduced to one whose size is bounded in terms of n and the syntactic complexity of the formulas whose truth we wish to remain invariant. This allows us to show that any finitely defined class of frames with finite diversity is computably reducible, from which decidability follows by Lemma 3.2.
Theorem 3.13. If
![]() $\Gamma \subseteq \mathcal {L}^O$
is finite and
$\Gamma \subseteq \mathcal {L}^O$
is finite and
![]() $\mathsf {R}(\Gamma )$
has finite diversity, then
$\mathsf {R}(\Gamma )$
has finite diversity, then
![]() $\mathcal {L}(\mathsf {R}(\Gamma ))$
is decidable.
$\mathcal {L}(\mathsf {R}(\Gamma ))$
is decidable.
Proof Assume
![]() $\Gamma \subseteq \mathcal {L}^O$
is finite and
$\Gamma \subseteq \mathcal {L}^O$
is finite and
![]() $\mathsf {R}(\Gamma )$
has diversity
$\mathsf {R}(\Gamma )$
has diversity
![]() $n\in \mathbb {N}$
. Let
$n\in \mathbb {N}$
. Let
![]() $l:=\mathrm {max}\{\mathrm {qd}(\nu (\gamma ^x)):\gamma \in \Gamma \}$
. Let
$l:=\mathrm {max}\{\mathrm {qd}(\nu (\gamma ^x)):\gamma \in \Gamma \}$
. Let
![]() $r:\mathbb {N}\to \mathbb {N}$
such that
$r:\mathbb {N}\to \mathbb {N}$
such that
![]() $r:m\mapsto n\cdot 2^{\mathrm {max}(m,l)}$
. We show that
$r:m\mapsto n\cdot 2^{\mathrm {max}(m,l)}$
. We show that
![]() $\mathsf {R}(\Gamma )$
is r-reducible; the claim follows by Lemma 3.2. So consider any
$\mathsf {R}(\Gamma )$
is r-reducible; the claim follows by Lemma 3.2. So consider any
![]() $m\in \mathbb {N}$
and point-generated subframe
$m\in \mathbb {N}$
and point-generated subframe
![]() $\mathfrak {F}$
of a frame in
$\mathfrak {F}$
of a frame in
![]() $\mathsf {R}(\Gamma )$
. Let
$\mathsf {R}(\Gamma )$
. Let
![]() $\mathfrak {F}'$
be
$\mathfrak {F}'$
be
![]() $\mathfrak {F}^{2^{\mathrm {max}(m,l)}}_{\mathrm {id}}$
. By Proposition 3.12,
$\mathfrak {F}^{2^{\mathrm {max}(m,l)}}_{\mathrm {id}}$
. By Proposition 3.12,
![]() $\mathfrak {F}$
and
$\mathfrak {F}$
and
![]() $\mathfrak {F}'$
are
$\mathfrak {F}'$
are
![]() $\mathrm {max}(m,l)$
-equivalent (and so also m-equivalent). Thus
$\mathrm {max}(m,l)$
-equivalent (and so also m-equivalent). Thus
![]() $\mathfrak {F}'$
validates
$\mathfrak {F}'$
validates
![]() $\Gamma $
, whence
$\Gamma $
, whence
![]() $\mathfrak {F}'$
is in
$\mathfrak {F}'$
is in
![]() $\mathsf {R}(\Gamma )$
. By construction, the size of
$\mathsf {R}(\Gamma )$
. By construction, the size of
![]() $\mathfrak {F}'$
is limited by
$\mathfrak {F}'$
is limited by
![]() $r(m)$
.
$r(m)$
.
As a first illustration of how Theorem 3.13 can be applied, we note that Fine and Kaplan’s result on the decidability of
![]() $\mathrm {S5}\pi +$
follows immediately:
$\mathrm {S5}\pi +$
follows immediately:
Example 3.14.
![]() $\mathsf {R}(\mathrm {S5})$
has diversity
$\mathsf {R}(\mathrm {S5})$
has diversity
![]() $1$
, and so
$1$
, and so
![]() $\mathrm {S5}\pi +$
is decidable.
$\mathrm {S5}\pi +$
is decidable.
Proof
![]() $\mathsf {R}(\mathrm {S5})$
is the class of unimodal frames with an equivalence relation. Point-generated subframes of such frames have a universal relation, and so diversity
$\mathsf {R}(\mathrm {S5})$
is the class of unimodal frames with an equivalence relation. Point-generated subframes of such frames have a universal relation, and so diversity
![]() $1$
. The claim follows by Theorem 3.13.
$1$
. The claim follows by Theorem 3.13.
More interestingly, the theorem can also be applied to the weaker logic
![]() $\mathrm {KE}$
(aka
$\mathrm {KE}$
(aka
![]() $\mathrm {K5}$
), which establishes our first new decidability result:
$\mathrm {K5}$
), which establishes our first new decidability result:
Example 3.15.
![]() $\mathsf {R}(\mathrm {KE})$
has diversity
$\mathsf {R}(\mathrm {KE})$
has diversity
![]() $3$
, and so
$3$
, and so
![]() $\mathrm {KE}\pi +$
is decidable.
$\mathrm {KE}\pi +$
is decidable.
Proof
![]() $\mathsf {R}(\mathrm {KE})$
is the class of relational frames with a Euclidean relation. Let
$\mathsf {R}(\mathrm {KE})$
is the class of relational frames with a Euclidean relation. Let
![]() $\mathfrak {F}$
be such a frame, w one of its worlds, and
$\mathfrak {F}$
be such a frame, w one of its worlds, and
![]() $\mathfrak {F}_w=\langle W,R\rangle $
. It is routine to show that then, either R is universal on W, or there is a set
$\mathfrak {F}_w=\langle W,R\rangle $
. It is routine to show that then, either R is universal on W, or there is a set
![]() $x\subseteq W\backslash \{w\}$
such that
$x\subseteq W\backslash \{w\}$
such that
![]() $vRu$
iff either
$vRu$
iff either
![]() $v=w$
and
$v=w$
and
![]() $u\in x$
, or
$u\in x$
, or
![]() $v\neq w$
and
$v\neq w$
and
![]() $u\neq w$
. Thus, the diversity of
$u\neq w$
. Thus, the diversity of
![]() $\mathfrak {F}_w$
is bounded by
$\mathfrak {F}_w$
is bounded by
![]() $3$
. The claim follows by Theorem 3.13.
$3$
. The claim follows by Theorem 3.13.
With Proposition 2.8 and the fact that
![]() $\Box \Box p\to \Box \Box \Box p\in \mathrm {KE}$
, it follows that
$\Box \Box p\to \Box \Box \Box p\in \mathrm {KE}$
, it follows that
![]() $\Lambda \pi +$
is decidable, for any finite axiomatic extension
$\Lambda \pi +$
is decidable, for any finite axiomatic extension
![]() $\Lambda $
of
$\Lambda $
of
![]() $\mathrm {KE}$
. We therefore obtain Example 3.14 as a corollary, as well as the result of Ding [Reference Ding10] on the decidability of
$\mathrm {KE}$
. We therefore obtain Example 3.14 as a corollary, as well as the result of Ding [Reference Ding10] on the decidability of
![]() $\mathrm {KD4E}\pi +$
. In fact, every normal extension of
$\mathrm {KD4E}\pi +$
. In fact, every normal extension of
![]() $\mathrm {KE}$
is finitely axiomatizable, as shown by Nagle and Thomason [Reference Nagle and Thomason40]. We conclude:
$\mathrm {KE}$
is finitely axiomatizable, as shown by Nagle and Thomason [Reference Nagle and Thomason40]. We conclude:
Corollary 3.16. If
![]() $\Lambda $
is a normal extension of
$\Lambda $
is a normal extension of
![]() $\mathrm {KE}$
, then
$\mathrm {KE}$
, then
![]() $\Lambda \pi +$
is decidable.
$\Lambda \pi +$
is decidable.
To illustrate the versatility of our decidability argument, and to delineate the axiomatizability boundary further from above, we consider another, more exotic, example of a unimodal logic.
Example 3.17.
![]() $\mathsf {R}(\mathrm {K1.2})$
has diversity
$\mathsf {R}(\mathrm {K1.2})$
has diversity
![]() $2$
, and so
$2$
, and so
![]() $\mathrm {K1.2}\pi +$
is decidable.
$\mathrm {K1.2}\pi +$
is decidable.
Proof The argument is analogous to the above cases, using the following observation: If
![]() $\mathfrak {F}$
validates
$\mathfrak {F}$
validates
![]() $\mathrm {K1.2}$
, then in any point-generated subframe
$\mathrm {K1.2}$
, then in any point-generated subframe
![]() $\mathfrak {F}_w$
, w can access only itself and worlds which can access only themselves. So the diversity of
$\mathfrak {F}_w$
, w can access only itself and worlds which can access only themselves. So the diversity of
![]() $\mathfrak {F}_w$
is bounded by
$\mathfrak {F}_w$
is bounded by
![]() $2$
.
$2$
.
So far, we have considered finitely axiomatized normal modal logics and the classes of relational frames they define. But the method developed here applies as well to finite sets of formulas involving propositional quantifiers and the classes of relational frames they define. By way of illustration, we consider the logic of “elsewhere” discussed by von Wright [Reference von Wright and Sosa57], which is the propositional modal logic of the class of frames in which every world can access every other world, but not itself. Segerberg [Reference Segerberg52] shows that this is the normal modal logic axiomatized by the axioms
![]() $\mathbf {B}$
and
$\mathbf {B}$
and
![]() $p\to (\Box p\to \Box \Box p)$
. Since these axioms are valid on frames with a universal relations, it follows that they fail to impose the requirement of irreflexivity on the class of relational frames they define. However, using propositional quantifiers, irreflexivity is easily captured by the negation of the universal closure of the axiom
$p\to (\Box p\to \Box \Box p)$
. Since these axioms are valid on frames with a universal relations, it follows that they fail to impose the requirement of irreflexivity on the class of relational frames they define. However, using propositional quantifiers, irreflexivity is easily captured by the negation of the universal closure of the axiom
![]() $\mathbf {T}$
. Adding this to the other two axioms, we define the class of frames whose point-generated subframes are in the intended class of frames. By Proposition 2.7, these two classes of frames have the same propositionally quantified modal logic. We can thus reason as follows:
$\mathbf {T}$
. Adding this to the other two axioms, we define the class of frames whose point-generated subframes are in the intended class of frames. By Proposition 2.7, these two classes of frames have the same propositionally quantified modal logic. We can thus reason as follows:
Example 3.18. Let
![]() $\mathsf {E}$
be the class of unimodal frames in which every world can access every other world, but not itself.
$\mathsf {E}$
be the class of unimodal frames in which every world can access every other world, but not itself.
![]() $\mathcal {L}(\mathsf {E})$
is decidable.
$\mathcal {L}(\mathsf {E})$
is decidable.
Proof Let
![]() $\Gamma =\{p\to \Box \Diamond p,p\to (\Box p\to \Box \Box p),\neg \forall p(\Box p\to p)\}$
. The frames of
$\Gamma =\{p\to \Box \Diamond p,p\to (\Box p\to \Box \Box p),\neg \forall p(\Box p\to p)\}$
. The frames of
![]() $\mathsf {E}$
are exactly the point-generated subframes of frames in
$\mathsf {E}$
are exactly the point-generated subframes of frames in
![]() $\mathsf {R}(\Gamma )$
. Since the frames of
$\mathsf {R}(\Gamma )$
. Since the frames of
![]() $\mathsf {E}$
have diversity 1,
$\mathsf {E}$
have diversity 1,
![]() $\mathsf {R}(\Gamma )$
has diversity 1. It follows by Theorem 3.13 that
$\mathsf {R}(\Gamma )$
has diversity 1. It follows by Theorem 3.13 that
![]() $\mathcal {L}(\mathsf {R}(\Gamma ))=\mathcal {L}(\mathsf {E})$
is decidable.
$\mathcal {L}(\mathsf {R}(\Gamma ))=\mathcal {L}(\mathsf {E})$
is decidable.
We postpone the discussion of decidability results for extensions of
![]() $\mathrm {K4.3}$
and multimodal logics; they will be discussed in Sections 5.2 and 6, respectively. Instead, the next section turns to the main unaxiomatizability results.
$\mathrm {K4.3}$
and multimodal logics; they will be discussed in Sections 5.2 and 6, respectively. Instead, the next section turns to the main unaxiomatizability results.
4 Recursive isomorphism to second-order logic
Fine [Reference Fine12] already noted that for several well-known normal modal logics
![]() $\Lambda $
,
$\Lambda $
,
![]() $\Lambda \pi +$
is not axiomatizable, by sketching a reduction of second-order arithmetic to these logics. The relevant logics consisted of a few logics included in
$\Lambda \pi +$
is not axiomatizable, by sketching a reduction of second-order arithmetic to these logics. The relevant logics consisted of a few logics included in
![]() $\mathrm {S4.2}$
, as well as
$\mathrm {S4.2}$
, as well as
![]() $\mathrm {B}$
. A more detailed exposition of the relevant reduction was eventually presented by Garson [Reference Garson, Gabbay and Guenthner18]. Kremer [Reference Kremer30] notes that these results can be strengthened to showing that the relevant logics
$\mathrm {B}$
. A more detailed exposition of the relevant reduction was eventually presented by Garson [Reference Garson, Gabbay and Guenthner18]. Kremer [Reference Kremer30] notes that these results can be strengthened to showing that the relevant logics
![]() $\Lambda \pi +$
are recursively isomorphic to second-order logic, using the techniques applied to propositionally quantified relevant logic in his paper. According to Kremer [Reference Kremer31, p. 530], Fine and Kripke had already proved the stronger claim of recursive isomorphism to second-order logic in unpublished work “shortly after the publication of” Fine [Reference Fine12]. Kaminski and Tiomkin [Reference Kaminski and Tiomkin26] present a more detailed construction showing that for every normal modal logic
$\Lambda \pi +$
are recursively isomorphic to second-order logic, using the techniques applied to propositionally quantified relevant logic in his paper. According to Kremer [Reference Kremer31, p. 530], Fine and Kripke had already proved the stronger claim of recursive isomorphism to second-order logic in unpublished work “shortly after the publication of” Fine [Reference Fine12]. Kaminski and Tiomkin [Reference Kaminski and Tiomkin26] present a more detailed construction showing that for every normal modal logic
![]() $\Lambda $
included in
$\Lambda $
included in
![]() $\mathrm {S4.2}$
, second-order logic is reducible to
$\mathrm {S4.2}$
, second-order logic is reducible to
![]() $\Lambda\pi+$
.
$\Lambda\pi+$
.
In this section, we will present a variation on the construction of Kaminski and Tiomkin [Reference Kaminski and Tiomkin26]. By making use of the result of Rabin and Scott and the symmetric second-order language
![]() $\mathcal {S}$
discussed in Section 2.4, we will be able to provide a construction which is both simpler and more versatile. Aside from providing a more accessible presentation, we show that we easily obtain, as corollaries, analogous results for a number of further logics, including
$\mathcal {S}$
discussed in Section 2.4, we will be able to provide a construction which is both simpler and more versatile. Aside from providing a more accessible presentation, we show that we easily obtain, as corollaries, analogous results for a number of further logics, including
![]() $\mathrm {B}$
and
$\mathrm {B}$
and
![]() $\mathrm {K4.2W}$
. We work with unimodal logics throughout this section.
$\mathrm {K4.2W}$
. We work with unimodal logics throughout this section.
4.1 Fully representing class of frames
Key to showing the recursive isomorphism of the relevant logic
![]() $\Lambda \pi +$
is proving that ssol, the set of validities of symmetric second-order logic, can be reduced to it. We proceed as follows: First, we define a formula
$\Lambda \pi +$
is proving that ssol, the set of validities of symmetric second-order logic, can be reduced to it. We proceed as follows: First, we define a formula
![]() $\mathrm {P}(i)$
of
$\mathrm {P}(i)$
of
![]() $\mathcal {L}^{\Box }$
with a free propositional variable i. Then, we show that if
$\mathcal {L}^{\Box }$
with a free propositional variable i. Then, we show that if
![]() $\mathrm {P}(i)$
is true in a world w of a relational frame, relative to an assignment function a, we can simulate first- and (symmetric) second-order quantification over
$\mathrm {P}(i)$
is true in a world w of a relational frame, relative to an assignment function a, we can simulate first- and (symmetric) second-order quantification over
![]() $D=R[w]\cap a(i)$
using
$D=R[w]\cap a(i)$
using
![]() $\mathcal {L}^{\Box }$
. First-order quantification is easily simulated, since we can represent an element
$\mathcal {L}^{\Box }$
. First-order quantification is easily simulated, since we can represent an element
![]() $d\in D$
using any proposition which is true in d and no other element of D. To simulate symmetric second-order quantification,
$d\in D$
using any proposition which is true in d and no other element of D. To simulate symmetric second-order quantification,
![]() $\mathrm {P}(i)$
will be formulated to guarantee that for any
$\mathrm {P}(i)$
will be formulated to guarantee that for any
![]() $d,e\in D$
, there is a world v which serves to represent the unordered pair
$d,e\in D$
, there is a world v which serves to represent the unordered pair
![]() $\{d,e\}$
. This is easily effected by requiring that any
$\{d,e\}$
. This is easily effected by requiring that any
![]() $f\in D$
can access v if and only if f is one of d and e. With this, it is easy to simulate quantification over symmetric relations on D, since any such relation corresponds to a set of representations of pairs, and so at least one proposition. This allows us to reduce second-order logic to any logic
$f\in D$
can access v if and only if f is one of d and e. With this, it is easy to simulate quantification over symmetric relations on D, since any such relation corresponds to a set of representations of pairs, and so at least one proposition. This allows us to reduce second-order logic to any logic
![]() $\Lambda \pi +$
such that for each cardinal
$\Lambda \pi +$
such that for each cardinal
![]() $\kappa $
, there is a world w of a frame validating
$\kappa $
, there is a world w of a frame validating
![]() $\Lambda $
in which
$\Lambda $
in which
![]() $\mathrm {P}(i)$
is true relative to some assignment function a such that
$\mathrm {P}(i)$
is true relative to some assignment function a such that
![]() $|R[w]\cap a(i)|=\kappa $
.
$|R[w]\cap a(i)|=\kappa $
.
We start making this outline precise by introducing abbreviations for formulas of
![]() $\mathcal {L}^{\Box }$
expressing the relevant concepts. First, as Fine [Reference Fine12] observed, propositional quantifiers allow us to state that p is true in just one of the accessible worlds, as follows:
$\mathcal {L}^{\Box }$
expressing the relevant concepts. First, as Fine [Reference Fine12] observed, propositional quantifiers allow us to state that p is true in just one of the accessible worlds, as follows:
-
 $\mathrm {Q}(p):=\Diamond p\wedge \forall q(\Box (p\to q)\vee \Box (p\to \neg q))$
.
$\mathrm {Q}(p):=\Diamond p\wedge \forall q(\Box (p\to q)\vee \Box (p\to \neg q))$
.
We use
![]() $\mathrm {Ind}(p)$
to state that p represents an individual (an element of the domain D); we use
$\mathrm {Ind}(p)$
to state that p represents an individual (an element of the domain D); we use
![]() $\mathrm {PotP}(p)$
to state that p is true in a single world of
$\mathrm {PotP}(p)$
to state that p is true in a single world of
![]() $R[R[w]]$
, and so potentially serves to represent an unordered pair of individuals; and we use
$R[R[w]]$
, and so potentially serves to represent an unordered pair of individuals; and we use
![]() $\mathrm {Pair}(p,q,r)$
to state that, assuming p and q represent individuals, r represents their unordered pair:
$\mathrm {Pair}(p,q,r)$
to state that, assuming p and q represent individuals, r represents their unordered pair:
-
 $\mathrm {Ind}(p):=\mathrm {Q}(p)\wedge \Diamond (p\wedge i)$
,
$\mathrm {Ind}(p):=\mathrm {Q}(p)\wedge \Diamond (p\wedge i)$
, -
 $\mathrm {PotP}(p):=\Diamond \Diamond p\wedge \forall q(\Box \Box (p\to q)\vee \Box \Box (p\to \neg q))$
,
$\mathrm {PotP}(p):=\Diamond \Diamond p\wedge \forall q(\Box \Box (p\to q)\vee \Box \Box (p\to \neg q))$
, -
 $\mathrm {Pair}(p,q,r):=\mathrm {PotP}(r)\wedge \forall s(\mathrm {Ind}(s)\to (\Diamond (s\wedge \Diamond r)\leftrightarrow \Diamond (s\wedge (p\vee q))))$
.
$\mathrm {Pair}(p,q,r):=\mathrm {PotP}(r)\wedge \forall s(\mathrm {Ind}(s)\to (\Diamond (s\wedge \Diamond r)\leftrightarrow \Diamond (s\wedge (p\vee q))))$
.
With these, we can define the formula
![]() $\mathrm {P}(i)$
, stating that for any p and q representing individuals, there is some r representing their unordered pair:
$\mathrm {P}(i)$
, stating that for any p and q representing individuals, there is some r representing their unordered pair:
-
 $\mathrm {P}(i):=\forall p\forall q(\mathrm {Ind}(p)\wedge \mathrm {Ind}(q)\to \exists r\mathrm {Pair}(p,q,r))$
.
$\mathrm {P}(i):=\forall p\forall q(\mathrm {Ind}(p)\wedge \mathrm {Ind}(q)\to \exists r\mathrm {Pair}(p,q,r))$
.
Before turning to the simulation of second-order logic, it will be useful to record what it takes for
![]() $\mathrm {P}(i)$
to be true.
$\mathrm {P}(i)$
to be true.
Definition 4.1. Let
![]() $\mathfrak {F}=\langle W,R\rangle $
be a relational frame,
$\mathfrak {F}=\langle W,R\rangle $
be a relational frame,
![]() $w\in W$
, and
$w\in W$
, and
![]() $I\subseteq W$
. w and I provide pairing if for all
$I\subseteq W$
. w and I provide pairing if for all
![]() $d,e\in R[w]\cap I$
, there is some
$d,e\in R[w]\cap I$
, there is some
![]() $v\in R[R[w]]$
such that for all
$v\in R[R[w]]$
such that for all
![]() $f\in R[w]\cap I$
,
$f\in R[w]\cap I$
,
![]() $fRv$
iff
$fRv$
iff
![]() $f\in \{d,e\}$
.
$f\in \{d,e\}$
.
Lemma 4.2. Let
![]() $\mathfrak {F}=\langle W,R\rangle $
be a relational frame,
$\mathfrak {F}=\langle W,R\rangle $
be a relational frame,
![]() $w\in W$
, and a an assignment function. Then
$w\in W$
, and a an assignment function. Then
![]() $\mathfrak {F},w,a\Vdash \mathrm {P}(i)$
iff w and
$\mathfrak {F},w,a\Vdash \mathrm {P}(i)$
iff w and
![]() $a(i)$
provide pairing.
$a(i)$
provide pairing.
Proof Note that
![]() $\mathfrak {F},w,a\Vdash \mathrm {Ind}(p)$
iff
$\mathfrak {F},w,a\Vdash \mathrm {Ind}(p)$
iff
![]() $R[w]\cap a(p)$
is a singleton subset of
$R[w]\cap a(p)$
is a singleton subset of
![]() $a(i)$
, and
$a(i)$
, and
![]() $\mathfrak {F},w,a\Vdash \mathrm {PotP}(p)$
iff
$\mathfrak {F},w,a\Vdash \mathrm {PotP}(p)$
iff
![]() $R[R[w]]\cap a(p)$
is a singleton. Further, if
$R[R[w]]\cap a(p)$
is a singleton. Further, if
![]() $R[w]\cap a(p)=\{d\}\subseteq a(i)$
and
$R[w]\cap a(p)=\{d\}\subseteq a(i)$
and
![]() $R[w]\cap a(q)=\{e\}\subseteq a(i)$
, then
$R[w]\cap a(q)=\{e\}\subseteq a(i)$
, then
![]() $\mathfrak {F},w,a\Vdash \mathrm {Pair}(p,q,r)$
iff
$\mathfrak {F},w,a\Vdash \mathrm {Pair}(p,q,r)$
iff
![]() $R[R[w]]\cap a(r)$
is a singleton
$R[R[w]]\cap a(r)$
is a singleton
![]() $\{v\}$
such that for all
$\{v\}$
such that for all
![]() $f\in R[w]\cap a(i)$
,
$f\in R[w]\cap a(i)$
,
![]() $fRv$
iff
$fRv$
iff
![]() $f\in \{d,e\}$
. With these observations, it is routine to establish the claim.
$f\in \{d,e\}$
. With these observations, it is routine to establish the claim.
The next step requires us to simulate
![]() $\mathcal {S}$
using
$\mathcal {S}$
using
![]() $\mathcal {L}^{\Box }$
. We assume that for every variable
$\mathcal {L}^{\Box }$
. We assume that for every variable
![]() $\xi $
of
$\xi $
of
![]() $\mathcal {S}$
(first- or second-order), there is a distinct propositional variable
$\mathcal {S}$
(first- or second-order), there is a distinct propositional variable
![]() $p_{\xi }$
. With this, we define the recursive mapping
$p_{\xi }$
. With this, we define the recursive mapping
![]() $\cdot ^*$
from
$\cdot ^*$
from
![]() $\mathcal {S}$
to
$\mathcal {S}$
to
![]() $\mathcal {L}^{\Box }$
whose only non-trivial clauses are the following:
$\mathcal {L}^{\Box }$
whose only non-trivial clauses are the following:
-
 $(Xyz)^*:=\exists r(\mathrm {Pair}(p_y,p_z,r)\wedge \Diamond \Diamond (r\wedge p_X))$
,
$(Xyz)^*:=\exists r(\mathrm {Pair}(p_y,p_z,r)\wedge \Diamond \Diamond (r\wedge p_X))$
, -
 $(\forall x\varphi )^*:=\forall p_x(\mathrm {Ind}(p_x)\to \varphi ^*)$
,
$(\forall x\varphi )^*:=\forall p_x(\mathrm {Ind}(p_x)\to \varphi ^*)$
, -
 $(\forall X\varphi )^*:=\forall p_X(\varphi ^*)$
.
$(\forall X\varphi )^*:=\forall p_X(\varphi ^*)$
.
The next lemma observes that this mapping works as intended.
Lemma 4.3. Let
![]() $\varphi \in \mathcal {S}$
. If
$\varphi \in \mathcal {S}$
. If
![]() $\mathfrak {F}=\langle W,R\rangle $
is a relational frame,
$\mathfrak {F}=\langle W,R\rangle $
is a relational frame,
![]() $w\in W$
,
$w\in W$
,
![]() $I\subseteq W$
, a an assignment function for
$I\subseteq W$
, a an assignment function for
![]() $\mathcal {S}$
on
$\mathcal {S}$
on
![]() $D=R[w]\cap I$
, and w and I provide pairing, then
$D=R[w]\cap I$
, and w and I provide pairing, then
where b is the assignment function such that
![]() $b(i)=I$
,
$b(i)=I$
,
![]() $b(p_x)=\{a(x)\}$
, and
$b(p_x)=\{a(x)\}$
, and
![]() $b(p_X)$
is the set of
$b(p_X)$
is the set of
![]() $v\in R[R[w]]$
for which there are d and e related by
$v\in R[R[w]]$
for which there are d and e related by
![]() $a(X)$
such that for every
$a(X)$
such that for every
![]() $f\in D$
,
$f\in D$
,
![]() $fRv$
iff
$fRv$
iff
![]() $f\in \{d,e\}$
.
$f\in \{d,e\}$
.
Proof By induction on the complexity of
![]() $\varphi $
. (The proof requires showing that formulas in the image of
$\varphi $
. (The proof requires showing that formulas in the image of
![]() $\varphi ^*$
are insensitive to the truth of
$\varphi ^*$
are insensitive to the truth of
![]() $p_x$
outside of
$p_x$
outside of
![]() $R[w]$
, but this is straightforward from the syntactic positions in which
$R[w]$
, but this is straightforward from the syntactic positions in which
![]() $p_x$
occurs in any such formula. A similar observation is required for
$p_x$
occurs in any such formula. A similar observation is required for
![]() $p_X$
.)
$p_X$
.)
With this lemma, we can simulate
![]() $\mathcal {S}$
on
$\mathcal {S}$
on
![]() $R[w]\cap I$
whenever w and I provide pairing. Thus, we can reduce ssol to
$R[w]\cap I$
whenever w and I provide pairing. Thus, we can reduce ssol to
![]() $\mathcal {L}(\mathsf {C})$
whenever
$\mathcal {L}(\mathsf {C})$
whenever
![]() $\mathsf {C}$
is a class of frames in which for every cardinality, we can find corresponding w and I which provide pairing. Formally, this condition on classes of frames is defined as follows:
$\mathsf {C}$
is a class of frames in which for every cardinality, we can find corresponding w and I which provide pairing. Formally, this condition on classes of frames is defined as follows:
Definition 4.4. Let a class of relational frames
![]() $\mathsf {C}$
fully represent if for every cardinality
$\mathsf {C}$
fully represent if for every cardinality
![]() $\kappa $
, there is a frame
$\kappa $
, there is a frame
![]() $\mathfrak {F}=\langle W,R\rangle $
in
$\mathfrak {F}=\langle W,R\rangle $
in
![]() $\mathsf {C}$
,
$\mathsf {C}$
,
![]() $w\in W$
and
$w\in W$
and
![]() $I\subseteq W$
such that w and I provide pairing, and
$I\subseteq W$
such that w and I provide pairing, and
![]() $|R[w]\cap I|=\kappa $
.
$|R[w]\cap I|=\kappa $
.
Due to the parameter I, a single frame may be a witness of full representation for many cardinalities. Nonetheless, since there is a proper class of cardinals, any class of relational frames which fully represents must be proper as well. We can now show that whenever
![]() $\mathsf {C}$
fully represents, ssol can be reduced to
$\mathsf {C}$
fully represents, ssol can be reduced to
![]() $\mathcal {L}(\mathsf {C})$
, from which it follows that if
$\mathcal {L}(\mathsf {C})$
, from which it follows that if
![]() $\mathcal{L}(\mathsf{C})$
is finitely definable, then it is recursively isomorphic to ssol (and so second-order logic as usually defined). In fact, the reduction generalizes to any set
$\mathcal{L}(\mathsf{C})$
is finitely definable, then it is recursively isomorphic to ssol (and so second-order logic as usually defined). In fact, the reduction generalizes to any set
![]() $\Pi \subseteq \mathcal {L}(\mathsf {C})$
, as long as
$\Pi \subseteq \mathcal {L}(\mathsf {C})$
, as long as
![]() $\Pi $
includes
$\Pi $
includes
![]() $\mathrm {K}\pi +$
.
$\mathrm {K}\pi +$
.
Theorem 4.5. Let
![]() $\mathsf {C}$
be a class of relational frames which fully represents, and let
$\mathsf {C}$
be a class of relational frames which fully represents, and let
![]() $\Pi \subseteq \mathcal {L}^{\Box }$
such that
$\Pi \subseteq \mathcal {L}^{\Box }$
such that
![]() $\mathrm {K}\pi +\subseteq \Pi \subseteq \mathcal {L}(\mathsf {C})$
. Then second-order logic is reducible to
$\mathrm {K}\pi +\subseteq \Pi \subseteq \mathcal {L}(\mathsf {C})$
. Then second-order logic is reducible to
![]() $\Pi $
. If
$\Pi $
. If
![]() $\mathsf{C}$
is also defined by a finite set of formulas, then
$\mathsf{C}$
is also defined by a finite set of formulas, then
![]() $\mathcal{L}(\mathsf{C})$
is recursively isomorphic to second-order logic.
$\mathcal{L}(\mathsf{C})$
is recursively isomorphic to second-order logic.
Proof As discussed in Section 2.4, it suffices to reduce second-order logic in the guise of ssol to
![]() $\Pi $
. (The conclusion of recursive isomorphism for a class of frames defined by a finite set from such a reduction is routine; for further details, see the corresponding discussion by Kremer [Reference Kremer30].) We may focus just on sentences (closed formulas) of
$\Pi $
. (The conclusion of recursive isomorphism for a class of frames defined by a finite set from such a reduction is routine; for further details, see the corresponding discussion by Kremer [Reference Kremer30].) We may focus just on sentences (closed formulas) of
![]() $\mathcal {S}$
. The required reduction is then provided by the function mapping any sentence
$\mathcal {S}$
. The required reduction is then provided by the function mapping any sentence
![]() $\varphi $
of
$\varphi $
of
![]() $\mathcal {S}$
to
$\mathcal {S}$
to
We show that
![]() iff
iff
![]() $\varphi ^{\dagger }\in \Pi $
.
$\varphi ^{\dagger }\in \Pi $
.
Assume first that
![]() $\varphi ^{\dagger }\notin \Pi $
. Then
$\varphi ^{\dagger }\notin \Pi $
. Then
![]() $\varphi ^{\dagger }\notin \mathrm {K}\pi +$
. So there is a relational frame
$\varphi ^{\dagger }\notin \mathrm {K}\pi +$
. So there is a relational frame
![]() $\mathfrak {F}=\langle W,R\rangle $
,
$\mathfrak {F}=\langle W,R\rangle $
,
![]() $w\in W$
and assignment function a such that
$w\in W$
and assignment function a such that
![]() $\mathfrak {F},w,a\Vdash \mathrm {P}(i)\wedge \neg \varphi ^*$
. By Lemma 4.2, w and
$\mathfrak {F},w,a\Vdash \mathrm {P}(i)\wedge \neg \varphi ^*$
. By Lemma 4.2, w and
![]() $a(i)$
provide pairing. Since
$a(i)$
provide pairing. Since
![]() $\varphi $
is closed, it follows by Lemma 4.3 that
$\varphi $
is closed, it follows by Lemma 4.3 that
![]() $\varphi $
is falsified by
$\varphi $
is falsified by
![]() $R[w]\cap a(i)$
. So
$R[w]\cap a(i)$
. So
![]() .
.
Assume now that
![]() $\varphi ^{\dagger }\in \Pi $
. Then
$\varphi ^{\dagger }\in \Pi $
. Then
![]() $\varphi ^{\dagger }\in \mathcal {L}(\mathsf {C})$
. Assume for contradiction that
$\varphi ^{\dagger }\in \mathcal {L}(\mathsf {C})$
. Assume for contradiction that
![]() . Then for some cardinality
. Then for some cardinality
![]() $\kappa $
, the sentence
$\kappa $
, the sentence
![]() $\varphi $
is falsified by any set of size
$\varphi $
is falsified by any set of size
![]() $\kappa $
. Since
$\kappa $
. Since
![]() $\mathsf {C}$
fully represents, there is a frame
$\mathsf {C}$
fully represents, there is a frame
![]() $\mathfrak {F}=\langle W,R\rangle $
in
$\mathfrak {F}=\langle W,R\rangle $
in
![]() $\mathsf {C}$
,
$\mathsf {C}$
,
![]() $w\in W$
and assignment function a such that w and
$w\in W$
and assignment function a such that w and
![]() $a(i)$
provide pairing, and
$a(i)$
provide pairing, and
![]() $|R[w]\cap a(i)|=\kappa $
. By Lemma 4.2,
$|R[w]\cap a(i)|=\kappa $
. By Lemma 4.2,
![]() $\mathfrak {F},w,a\Vdash \mathrm {P}(i)$
. Since
$\mathfrak {F},w,a\Vdash \mathrm {P}(i)$
. Since
![]() $\varphi $
is closed and falsified by
$\varphi $
is closed and falsified by
![]() $R[w]\cap a(i)$
, it follows with Lemma 4.3 that
$R[w]\cap a(i)$
, it follows with Lemma 4.3 that
![]() $\mathfrak {F},w,a\nVdash \varphi ^*$
. Thus
$\mathfrak {F},w,a\nVdash \varphi ^*$
. Thus
![]() $\mathfrak {F},w\nVdash \varphi ^{\dagger }$
, contradicting
$\mathfrak {F},w\nVdash \varphi ^{\dagger }$
, contradicting
![]() $\varphi ^{\dagger }\in \mathcal {L}(\mathsf {C})$
. So
$\varphi ^{\dagger }\in \mathcal {L}(\mathsf {C})$
. So
![]() .
.
4.2 Examples
From Theorem 4.5, we can conclude for any finitely axiomatized normal modal logic
![]() $\Lambda$
that
$\Lambda$
that
![]() $\Lambda \pi +$
is recursively isomorphic to second-order logic by showing that
$\Lambda \pi +$
is recursively isomorphic to second-order logic by showing that
![]() $\mathsf {R}(\Lambda )$
fully represents. The details depend on
$\mathsf {R}(\Lambda )$
fully represents. The details depend on
![]() $\Lambda $
, but in many cases, the frames witnessing full representation can be derived from a relatively simple class of frames, which we now introduce. In the following, we assume that every cardinal
$\Lambda $
, but in many cases, the frames witnessing full representation can be derived from a relatively simple class of frames, which we now introduce. In the following, we assume that every cardinal
![]() $\kappa $
is a set of size
$\kappa $
is a set of size
![]() $\kappa $
, and write
$\kappa $
, and write
![]() $U(\kappa )$
for the set of unordered pairs of elements of
$U(\kappa )$
for the set of unordered pairs of elements of
![]() $\kappa $
, i.e.,
$\kappa $
, i.e.,
![]() $\{\{d,e\}:d,e\in \kappa \}$
. We assume that
$\{\{d,e\}:d,e\in \kappa \}$
. We assume that
![]() $\kappa $
,
$\kappa $
,
![]() $U(\kappa )$
, and
$U(\kappa )$
, and
![]() $\{\kappa ^+\}$
are pairwise disjoint. This is not guaranteed by the usual von Neumann definition of ordinals, as
$\{\kappa ^+\}$
are pairwise disjoint. This is not guaranteed by the usual von Neumann definition of ordinals, as
![]() $\{0,1\}=2\in 3$
, but the problem is easily overcome by considering the disjoint union of the relevant sets—we omit the details for simplicity.
$\{0,1\}=2\in 3$
, but the problem is easily overcome by considering the disjoint union of the relevant sets—we omit the details for simplicity.
Definition 4.6. If
![]() $\kappa $
is a cardinal,
$\kappa $
is a cardinal,
![]() $\mathfrak {F}_{\kappa }$
is the relational frame
$\mathfrak {F}_{\kappa }$
is the relational frame
![]() $\langle W,R\rangle $
such that:
$\langle W,R\rangle $
such that:
-
 $W=\{\kappa ^+\}\cup \kappa \cup U(\kappa )$
,
$W=\{\kappa ^+\}\cup \kappa \cup U(\kappa )$
, -
 $R=\{\langle \kappa ^+,w\rangle :w\in \kappa \}\cup \{\langle w,v\rangle :w\in \kappa $
,
$R=\{\langle \kappa ^+,w\rangle :w\in \kappa \}\cup \{\langle w,v\rangle :w\in \kappa $
,
 $v\in U(\kappa )$
, and
$v\in U(\kappa )$
, and
 $w\in v\}$
.
$w\in v\}$
.
![]() $\mathfrak {F}_{\kappa }$
is constructed just so that
$\mathfrak {F}_{\kappa }$
is constructed just so that
![]() $\kappa ^+$
and
$\kappa ^+$
and
![]() $\kappa $
provide pairing, and
$\kappa $
provide pairing, and
![]() $|R[\kappa ^+]\cap \kappa |=\kappa $
, which can easily be verified. Therefore the class of relational frames fully represents, from which we can draw the following conclusion:
$|R[\kappa ^+]\cap \kappa |=\kappa $
, which can easily be verified. Therefore the class of relational frames fully represents, from which we can draw the following conclusion:
Example 4.7.
![]() $\mathrm {K}\pi +$
is recursively isomorphic to second-order logic.
$\mathrm {K}\pi +$
is recursively isomorphic to second-order logic.
Proof Since the class of relational frames fully represents, the claim follows by Theorem 4.5.
More interestingly,
![]() $\mathfrak {F}_{\kappa }$
is easily adapted to meet a number of additional requirements, while
$\mathfrak {F}_{\kappa }$
is easily adapted to meet a number of additional requirements, while
![]() $\kappa ^+$
and
$\kappa ^+$
and
![]() $\kappa $
still provide pairing. For example, we can take the transitive closure of R, and so obtain frames validating the
$\kappa $
still provide pairing. For example, we can take the transitive closure of R, and so obtain frames validating the
![]() $\mathbf {4}$
axiom. Adding also a “final” world, seen by every world, we obtain a simple proof of the result of Kaminski and Tiomkin [Reference Kaminski and Tiomkin26] that
$\mathbf {4}$
axiom. Adding also a “final” world, seen by every world, we obtain a simple proof of the result of Kaminski and Tiomkin [Reference Kaminski and Tiomkin26] that
![]() $\mathrm {S4.2}\pi +$
is recursively isomorphic to second-order logic. In fact, we note that the result can be strengthened in two ways: First,
$\mathrm {S4.2}\pi +$
is recursively isomorphic to second-order logic. In fact, we note that the result can be strengthened in two ways: First,
![]() $\mathrm {S4.2}$
can be strengthened to
$\mathrm {S4.2}$
can be strengthened to
![]() $\mathrm {K2.1}$
. Second, the result extends to
$\mathrm {K2.1}$
. Second, the result extends to
![]() $\Lambda \pi +$
for every finitely axiomatized normal modal logic
$\Lambda \pi +$
for every finitely axiomatized normal modal logic
![]() $\Lambda \subseteq \mathrm {K2.1}$
, and the resulting unaxiomatizability extends to every subset of formulas which includes
$\Lambda \subseteq \mathrm {K2.1}$
, and the resulting unaxiomatizability extends to every subset of formulas which includes
![]() $\mathrm {K}\pi +$
.
$\mathrm {K}\pi +$
.
Example 4.8. Second-order logic is reducible to every set of formulas
![]() $\Pi $
such that
$\Pi $
such that
![]() $\mathrm{K}\pi+\subseteq\Pi\subseteq\mathrm{K2.1}\pi+$
. For every finitely axiomatized normal modal logic
$\mathrm{K}\pi+\subseteq\Pi\subseteq\mathrm{K2.1}\pi+$
. For every finitely axiomatized normal modal logic
![]() $\Lambda\subseteq\mathrm{K2.1}$
,
$\Lambda\subseteq\mathrm{K2.1}$
,
![]() $\Lambda\pi+$
is recursively isomorphic to second-order logic.
$\Lambda\pi+$
is recursively isomorphic to second-order logic.
Proof Consider a frame
![]() $\mathfrak {F}_{\kappa }$
, and add a new “final” world f, which every other world can access. Take the reflexive and transitive closure of the accessibility relation of this extended frame. In the resulting frame,
$\mathfrak {F}_{\kappa }$
, and add a new “final” world f, which every other world can access. Take the reflexive and transitive closure of the accessibility relation of this extended frame. In the resulting frame,
![]() $\kappa ^+$
and
$\kappa ^+$
and
![]() $\kappa $
still provide pairing, while
$\kappa $
still provide pairing, while
![]() $\mathrm {K2.1}$
is valid. So
$\mathrm {K2.1}$
is valid. So
![]() $\mathsf {C}(\mathrm {K2.1})$
fully represents, whence the claim follows by Theorem 4.5.
$\mathsf {C}(\mathrm {K2.1})$
fully represents, whence the claim follows by Theorem 4.5.
Analogously, we can cover the case of
![]() $\mathrm {B}$
, which is mentioned by Fine [Reference Fine12] and Kremer [Reference Kremer30], but not discussed by Kaminski and Tiomkin [Reference Kaminski and Tiomkin26].
$\mathrm {B}$
, which is mentioned by Fine [Reference Fine12] and Kremer [Reference Kremer30], but not discussed by Kaminski and Tiomkin [Reference Kaminski and Tiomkin26].
Example 4.9. Second-order logic is reducible to every set of formulas
![]() $\Pi $
such that
$\Pi $
such that
![]() $\mathrm{K}\pi+\subseteq\Pi\subseteq\mathrm{B}\pi+$
. For every finitely axiomatized normal modal logic
$\mathrm{K}\pi+\subseteq\Pi\subseteq\mathrm{B}\pi+$
. For every finitely axiomatized normal modal logic
![]() $\Lambda\subseteq\mathrm{B}$
,
$\Lambda\subseteq\mathrm{B}$
,
![]() $\Lambda\pi+$
is recursively isomorphic to second-order logic.
$\Lambda\pi+$
is recursively isomorphic to second-order logic.
Proof Consider a frame
![]() $\mathfrak {F}_{\kappa }$
, and take the reflexive and symmetric closure of the accessibility relation. In the resulting frame,
$\mathfrak {F}_{\kappa }$
, and take the reflexive and symmetric closure of the accessibility relation. In the resulting frame,
![]() $\kappa ^+$
and
$\kappa ^+$
and
![]() $\kappa $
still provide pairing, while
$\kappa $
still provide pairing, while
![]() $\mathrm {B}$
is valid. So
$\mathrm {B}$
is valid. So
![]() $\mathsf {C}(\mathrm {B})$
fully represents, whence the claim follows by Theorem 4.5.
$\mathsf {C}(\mathrm {B})$
fully represents, whence the claim follows by Theorem 4.5.
We can also cover the case of
![]() $\mathrm {K4.2W}$
, which appears not to have been considered in the literature so far. This subsumes the case of
$\mathrm {K4.2W}$
, which appears not to have been considered in the literature so far. This subsumes the case of
![]() $\mathrm {KW}$
, which is better known in the context of provability logic as
$\mathrm {KW}$
, which is better known in the context of provability logic as
![]() $\mathrm {GL}$
; see [Reference Boolos5].
$\mathrm {GL}$
; see [Reference Boolos5].
Example 4.10. Second-order logic is reducible to every set of formulas
![]() $\Pi $
such that
$\Pi $
such that
![]() $\mathrm{K}\pi+\subseteq\Pi\subseteq\mathrm{K4.2W}\pi+$
. For every finitely axiomatized normal modal logic
$\mathrm{K}\pi+\subseteq\Pi\subseteq\mathrm{K4.2W}\pi+$
. For every finitely axiomatized normal modal logic
![]() $\Lambda\subseteq\mathrm{K4.2W}$
,
$\Lambda\subseteq\mathrm{K4.2W}$
,
![]() $\Lambda\pi+$
is recursively isomorphic to second-order logic.
$\Lambda\pi+$
is recursively isomorphic to second-order logic.
Proof Analogous to Example 4.8, using the transitive closure instead of the transitive and reflexive closure of the accessibility relation.
Inspecting the structure of the frames used in these proofs, it is easy to see that these results can be strengthened further in various ways to some less commonly considered modal logics. For example, the frames used in the proof of Example 4.10 all do not admit any path along the accessibility relation with more than three steps. Thus,
![]() $\mathrm {K4.2W}$
can be strengthened by adding
$\mathrm {K4.2W}$
can be strengthened by adding
![]() $\Box \Box \Box \Box \bot $
as an axiom. These strengthened logics also need not be finitely axiomatizable for the reduction of second-order logic to be possible. An example is the logic
$\Box \Box \Box \Box \bot $
as an axiom. These strengthened logics also need not be finitely axiomatizable for the reduction of second-order logic to be possible. An example is the logic
![]() $\mathrm {BSeg}$
, which Hughes and Cresswell [Reference Hughes and Cresswell24] show not to be finitely axiomatizable. This normal modal logic is obtained by adding to
$\mathrm {BSeg}$
, which Hughes and Cresswell [Reference Hughes and Cresswell24] show not to be finitely axiomatizable. This normal modal logic is obtained by adding to
![]() $\mathrm {B}$
every instance of the following axiom schema for
$\mathrm {B}$
every instance of the following axiom schema for
![]() $n\geq 1$
:
$n\geq 1$
:
-
 $\mathbf {Seg}_n:=\bigwedge ^n_{i=1}\Diamond \Diamond p_i\to \Diamond \bigwedge ^n_{i=1}\Diamond p_i$
.
$\mathbf {Seg}_n:=\bigwedge ^n_{i=1}\Diamond \Diamond p_i\to \Diamond \bigwedge ^n_{i=1}\Diamond p_i$
.
The reduction of second-order logic in Example 4.9 can be extended to
![]() $\mathrm {BSeg}$
by enriching the accessibility relation of any frame
$\mathrm {BSeg}$
by enriching the accessibility relation of any frame
![]() $\mathfrak {F}_{\kappa }$
, letting
$\mathfrak {F}_{\kappa }$
, letting
![]() $\kappa ^+$
access every world and every world access
$\kappa ^+$
access every world and every world access
![]() $\kappa ^+$
.
$\kappa ^+$
.
5 Extensions of
 $\mathrm {K4.3}$
$\mathrm {K4.3}$
The extensions of the unimodal logic
![]() $\mathrm {K4.3}$
constitute a special case, requiring special treatment for both decidability and unaxiomatizability results. We therefore treat them separately in this section. The classes of frames they define are somewhat more complicated to describe, so we start by introducing the relevant notions. We then consider decidable and unaxiomatizable logics in turn.
$\mathrm {K4.3}$
constitute a special case, requiring special treatment for both decidability and unaxiomatizability results. We therefore treat them separately in this section. The classes of frames they define are somewhat more complicated to describe, so we start by introducing the relevant notions. We then consider decidable and unaxiomatizable logics in turn.
5.1 Linear orders and balloons
We first recall the standard order-theoretic notion of a linear order.
Definition 5.1. Let W be a set and R a binary relation on W.
-
• R is connected if for all w and v in W,
 $wRv$
,
$wRv$
,
 $w=v$
, or
$w=v$
, or
 $vRw$
.
$vRw$
. -
• R is a linear order if R is a connected partial order (i.e., if R is connected, reflexive, transitive, and antisymmetric).
When no confusion is likely to arise, we identify an ordered set with its ordering relation. Note that a binary relation on a finite set is a linear order just in case it is isomorphic to a finite initial segment
![]() $\{0,\dots ,n\}$
of the natural numbers under their natural order
$\{0,\dots ,n\}$
of the natural numbers under their natural order
![]() $\leq $
.
$\leq $
.
Next, we introduce the notion of a balloon, which we take from [Reference Chagrov and Zakharyaschev9, pp. 103–104]. Note that the sets H and T in this definitions may be empty.
Definition 5.2. Let W be a set and R a binary relation on W. R is a reflexive (irreflexive) balloon if W is the disjoint union of two sets
![]() $T=\{t_1,\dots ,t_n\}$
and H such that
$T=\{t_1,\dots ,t_n\}$
and H such that
![]() $wRv$
iff either
$wRv$
iff either
![]() $w=t_i$
and
$w=t_i$
and
![]() $v=t_j$
, for
$v=t_j$
, for
![]() $i\leq j$
(
$i\leq j$
(
![]() $i<j$
), or
$i<j$
), or
![]() $v\in H$
.
$v\in H$
.
With these notions, many classes of frames defined by extensions of
![]() $\mathrm {K4.3}$
can be described. For example,
$\mathrm {K4.3}$
can be described. For example,
![]() $\mathrm {K4.3}$
itself is valid on just those relational frames whose point-generated subframes have an accessibility relation which is transitive and connected. With this, it is easy to see that
$\mathrm {K4.3}$
itself is valid on just those relational frames whose point-generated subframes have an accessibility relation which is transitive and connected. With this, it is easy to see that
![]() $\mathrm {K3}$
is valid on every linear order with an endpoint (a world which is accessible from every world). Aside from this, we will also need an account of the classes of relational frames defined by
$\mathrm {K3}$
is valid on every linear order with an endpoint (a world which is accessible from every world). Aside from this, we will also need an account of the classes of relational frames defined by
![]() $\mathrm {S4.3.1}$
and
$\mathrm {S4.3.1}$
and
![]() $\mathrm {K4.3Z}$
. This is provided by the following lemma:
$\mathrm {K4.3Z}$
. This is provided by the following lemma:
Lemma 5.3. Let
![]() $\mathfrak {F}=\langle W,R\rangle $
be a point-generated relational frame.
$\mathfrak {F}=\langle W,R\rangle $
be a point-generated relational frame.
-
(a)
 $\mathrm {S4.3.1}$
is valid on
$\mathrm {S4.3.1}$
is valid on
 $\mathfrak {F}$
just in case one of the following two conditions obtains:
$\mathfrak {F}$
just in case one of the following two conditions obtains:-
(i) R is a reflexive balloon.
-
(ii)
 $\mathfrak {F}$
is isomorphic to
$\mathfrak {F}$
is isomorphic to
 $\langle \mathbb {N},\leq \rangle $
.
$\langle \mathbb {N},\leq \rangle $
.
-
-
(b)
 $\mathrm {K4.3Z}$
is valid on
$\mathrm {K4.3Z}$
is valid on
 $\mathfrak {F}$
just in case one of the following two conditions obtains:
$\mathfrak {F}$
just in case one of the following two conditions obtains:-
(i) R is an irreflexive balloon.
-
(ii)
 $\mathfrak {F}$
is isomorphic to
$\mathfrak {F}$
is isomorphic to
 $\langle \mathbb {N},<\rangle $
.
$\langle \mathbb {N},<\rangle $
.
-
Proof The arguments are routine. A statement equivalent to (a) is also given by Reynolds and Zakharyaschev [Reference Reynolds and Zakharyaschev49, p. 912].
5.2 Decidable logics
In this section, we will show that the two logics just considered,
![]() $\mathrm {S4.3.1}$
and
$\mathrm {S4.3.1}$
and
![]() $\mathrm {K4.3Z}$
, define classes of relational frames whose propositionally quantified modal logic is decidable. We do so by showing that the propositionally quantified modal logics of the various kinds of frames mentioned in Lemma 5.3 are decidable.
$\mathrm {K4.3Z}$
, define classes of relational frames whose propositionally quantified modal logic is decidable. We do so by showing that the propositionally quantified modal logics of the various kinds of frames mentioned in Lemma 5.3 are decidable.
The case of the natural numbers under their natural order is already discussed by Fine [Reference Fine12, p. 344]. As Fine notes, the decidability of the propositionally quantified modal logic of the single frame consisting of the natural numbers and their natural ordering follows from the decidability of monadic second-order logic over this frame, and the decidability of this monadic second-order theory was shown by Büchi [Reference Büchi, Nagel, Suppes and Tarski6]. This monadic second-order theory is known in the literature as
![]() $\mathrm {S1S}$
. Fine does not specify whether the intended natural order is
$\mathrm {S1S}$
. Fine does not specify whether the intended natural order is
![]() $\leq $
or
$\leq $
or
![]() $<$
, but the difference is immaterial: it is easy to see that the monadic second-order theories of the two orders are recursively isomorphic. Thus:
$<$
, but the difference is immaterial: it is easy to see that the monadic second-order theories of the two orders are recursively isomorphic. Thus:
Lemma 5.4. If
![]() $\mathsf {C}$
is the singleton of
$\mathsf {C}$
is the singleton of
![]() $\langle \mathbb {N},\leq \rangle $
or the singleton of
$\langle \mathbb {N},\leq \rangle $
or the singleton of
![]() $\langle \mathbb {N},<\rangle $
, then
$\langle \mathbb {N},<\rangle $
, then
![]() $\mathcal {L}(\mathsf {C})$
is decidable.
$\mathcal {L}(\mathsf {C})$
is decidable.
Proof Using the standard translation, this is immediate by Proposition 2.9 and the decidability of
![]() $\mathrm {S1S}$
.
$\mathrm {S1S}$
.
The remaining case of balloons requires a bit more thought. The most immediate difficulty is the fact that in a balloon, the cluster of worlds H among which the accessibility relation is universal may be of arbitrary size. It is initially not obvious that it is possible to suitably represent such an arbitrarily large set H using a finite or countably infinite set of natural numbers, in a reduction to
![]() $\mathrm {S1S}$
. However, using the techniques developed in Section 3, it is easy to see that H may always be assumed to be finite. With this, the reduction is straightforward.
$\mathrm {S1S}$
. However, using the techniques developed in Section 3, it is easy to see that H may always be assumed to be finite. With this, the reduction is straightforward.
Lemma 5.5. If
![]() $\mathsf {C}$
is the class of reflexive balloons or the class of irreflexive balloons, then
$\mathsf {C}$
is the class of reflexive balloons or the class of irreflexive balloons, then
![]() $\mathcal {L}(\mathsf {C})$
is decidable.
$\mathcal {L}(\mathsf {C})$
is decidable.
Proof We consider the irreflexive case; the reflexive case follows similarly. Along the lines of Lemma 5.4, it suffices to reduce
![]() $\mathcal {M}(\mathsf {C})$
to
$\mathcal {M}(\mathsf {C})$
to
![]() $\mathrm {S1S}$
, which we take to be the monadic second-order theory of the single frame
$\mathrm {S1S}$
, which we take to be the monadic second-order theory of the single frame
![]() $\langle \mathbb {N},<\rangle $
. First, note that if
$\langle \mathbb {N},<\rangle $
. First, note that if
![]() $\varphi \in \mathcal {N}^{\Box }$
is satisfiable on some reflexive balloon
$\varphi \in \mathcal {N}^{\Box }$
is satisfiable on some reflexive balloon
![]() $\mathfrak {F}$
in
$\mathfrak {F}$
in
![]() $\mathsf {C}$
, then by Proposition 3.12,
$\mathsf {C}$
, then by Proposition 3.12,
![]() $\varphi $
is also satisfiable on
$\varphi $
is also satisfiable on
![]() $\mathfrak {F}^{2^n}_{\mathrm {id}}$
, where
$\mathfrak {F}^{2^n}_{\mathrm {id}}$
, where
![]() $n=\mathrm {qd}(\varphi )$
, and so on a frame in the class of finite reflexive balloons
$n=\mathrm {qd}(\varphi )$
, and so on a frame in the class of finite reflexive balloons
![]() $\mathsf {F}$
. Thus
$\mathsf {F}$
. Thus
![]() $\mathcal {M}(\mathsf {C})$
is
$\mathcal {M}(\mathsf {C})$
is
![]() $\mathcal {M}(\mathsf {F})$
, so we may reduce
$\mathcal {M}(\mathsf {F})$
, so we may reduce
![]() $\mathcal {M}(\mathsf {F})$
to
$\mathcal {M}(\mathsf {F})$
to
![]() $\mathrm {S1S}$
.
$\mathrm {S1S}$
.
The required reduction is provided by the recursive mapping with the following non-trivial clauses (with t and h bound by initial existential quantifiers):
-
 $(Rxy)^{th}:=Rxy\vee \neg Ryt$
,
$(Rxy)^{th}:=Rxy\vee \neg Ryt$
, -
 $(\forall x\psi )^{th}:=\forall x(Rxh\to \psi ^{th})$
.
$(\forall x\psi )^{th}:=\forall x(Rxh\to \psi ^{th})$
.
This reduction simulates finite balloons using two numbers t and h as parameters: the numbers less than t and h represent T, and the remaining numbers less than h represent H. It is routine to show that
![]() $\varphi $
is valid over
$\varphi $
is valid over
![]() $\mathsf {F}$
iff
$\mathsf {F}$
iff
![]() $\varphi ^*\in \mathrm {S1S}$
, as required.
$\varphi ^*\in \mathrm {S1S}$
, as required.
With these results, it is straightforward to establish our first example, which further delimits the axiomatizability boundary of Figure 1:
Example 5.6.
![]() $\mathrm {S4.3.1}\pi +$
is decidable.
$\mathrm {S4.3.1}\pi +$
is decidable.
Proof Let
![]() $\mathsf {B}$
be the class of reflexive balloons, and
$\mathsf {B}$
be the class of reflexive balloons, and
![]() $\mathsf {N}$
the singleton of
$\mathsf {N}$
the singleton of
![]() $\langle \mathbb {N},\leq \rangle $
. By Lemma 5.3(a),
$\langle \mathbb {N},\leq \rangle $
. By Lemma 5.3(a),
![]() $\mathrm {S4.3.1}\pi +$
is
$\mathrm {S4.3.1}\pi +$
is
![]() $\mathcal {L}(\mathsf {B})\cap \mathcal {L}(\mathsf {N})$
. The decidability of this logic follows from Lemmas 5.4 and 5.5.
$\mathcal {L}(\mathsf {B})\cap \mathcal {L}(\mathsf {N})$
. The decidability of this logic follows from Lemmas 5.4 and 5.5.
Moreover, Fine [Reference Fine13] has shown that all normal extensions of
![]() $\mathrm {S4.3}$
are finitely axiomatizable. As in the case of
$\mathrm {S4.3}$
are finitely axiomatizable. As in the case of
![]() $\mathrm {KE}$
, we can therefore conclude:
$\mathrm {KE}$
, we can therefore conclude:
Corollary 5.7. If
![]() $\Lambda $
is a normal extension of
$\Lambda $
is a normal extension of
![]() $\mathrm {S4.3.1}$
, then
$\mathrm {S4.3.1}$
, then
![]() $\Lambda \pi +$
is decidable.
$\Lambda \pi +$
is decidable.
It is worth noting that Segerberg [Reference Segerberg51] showed in the standard quantifier-free setting that
![]() $\mathrm {S4.3.1}$
is the modal logic of the single frame
$\mathrm {S4.3.1}$
is the modal logic of the single frame
![]() $\langle \mathbb {N},\leq \rangle $
; a fortiori, it is also the modal logic of the class of frames it defines. Although these classes of frames have the same quantifier-free modal logic, and both give rise to decidable propositionally quantified modal logics (by Lemma 5.4 and Example 5.6), these propositionally quantified modal logics are not the same: with the additional expressive power of propositional quantifiers, balloons can be distinguished from
$\langle \mathbb {N},\leq \rangle $
; a fortiori, it is also the modal logic of the class of frames it defines. Although these classes of frames have the same quantifier-free modal logic, and both give rise to decidable propositionally quantified modal logics (by Lemma 5.4 and Example 5.6), these propositionally quantified modal logics are not the same: with the additional expressive power of propositional quantifiers, balloons can be distinguished from
![]() $\langle \mathbb {N},\leq \rangle $
, for example using the sentence
$\langle \mathbb {N},\leq \rangle $
, for example using the sentence
![]() $\Diamond \bar {\forall }\mathbf {5}$
.
$\Diamond \bar {\forall }\mathbf {5}$
.
Our second example is established in just the same way as the first:
Example 5.8.
![]() $\mathrm {K4.3Z}\pi +$
is decidable.
$\mathrm {K4.3Z}\pi +$
is decidable.
Proof Analogous to Example 5.6.
We can use this example to justify the earlier assertion that the requirement of finiteness in Proposition 2.8 cannot be weakened to recursive enumerability, even among quantifier-free sets of formulas: there is a normal modal logic
![]() $\Lambda $
obtained by strengthening
$\Lambda $
obtained by strengthening
![]() $\mathrm {K4.3Z}$
using a recursively enumerable set of axioms such that
$\mathrm {K4.3Z}$
using a recursively enumerable set of axioms such that
![]() $\Lambda \pi +$
is undecidable. This follows from the following result:
$\Lambda \pi +$
is undecidable. This follows from the following result:
Proposition 5.9. Any set
![]() $x\subseteq \mathbb {N}$
is reducible to
$x\subseteq \mathbb {N}$
is reducible to
![]() $(\mathrm {K4.3Z}+\Gamma _x)\pi +$
, where
$(\mathrm {K4.3Z}+\Gamma _x)\pi +$
, where
![]() $\Gamma _x=\{\Box ^n\Diamond \top :n\in x\}$
.
$\Gamma _x=\{\Box ^n\Diamond \top :n\in x\}$
.
Proof We show that
![]() $n\in x$
iff
$n\in x$
iff
![]() $\Box ^n\Diamond \top \in (\mathrm {K4.3Z}+\Gamma _x)\pi +$
. The left to right direction is immediate. For the right to left direction, assume
$\Box ^n\Diamond \top \in (\mathrm {K4.3Z}+\Gamma _x)\pi +$
. The left to right direction is immediate. For the right to left direction, assume
![]() $n\notin x$
, and let
$n\notin x$
, and let
![]() $\mathfrak {F}$
be a finite irreflexive linear order of length
$\mathfrak {F}$
be a finite irreflexive linear order of length
![]() $n+1$
.
$n+1$
.
![]() $\mathfrak {F}$
validates
$\mathfrak {F}$
validates
![]() $\mathrm {K4.3Z}+\Gamma _x$
but not
$\mathrm {K4.3Z}+\Gamma _x$
but not
![]() $\Box ^n\Diamond \top $
, whence
$\Box ^n\Diamond \top $
, whence
![]() $\Box ^n\Diamond \top \notin (\mathrm {K4.3Z}+\Gamma _x)\pi +$
.
$\Box ^n\Diamond \top \notin (\mathrm {K4.3Z}+\Gamma _x)\pi +$
.
If
![]() $x\subseteq \mathbb {N}$
is recursively enumerable but not decidable, it follows that
$x\subseteq \mathbb {N}$
is recursively enumerable but not decidable, it follows that
![]() $(\mathrm {K4.3Z}+\Gamma _x)\pi +$
is not decidable either, even though
$(\mathrm {K4.3Z}+\Gamma _x)\pi +$
is not decidable either, even though
![]() $\mathrm {K4.3Z}+\Gamma _x$
extends
$\mathrm {K4.3Z}+\Gamma _x$
extends
![]() $\mathrm {K4.3Z}$
using a recursively enumerable set
$\mathrm {K4.3Z}$
using a recursively enumerable set
![]() $\Gamma _x$
, and
$\Gamma _x$
, and
![]() $\mathrm {K4.3Z}\pi +$
is decidable. Similarly, if
$\mathrm {K4.3Z}\pi +$
is decidable. Similarly, if
![]() $x\subseteq \mathbb {N}$
is not recursively enumerable, then neither is
$x\subseteq \mathbb {N}$
is not recursively enumerable, then neither is
![]() $(\mathrm {K4.3Z}+\Gamma _x)\pi +$
, so the axiomatizability boundary cannot be extended to all normal modal logics.
$(\mathrm {K4.3Z}+\Gamma _x)\pi +$
, so the axiomatizability boundary cannot be extended to all normal modal logics.
5.3 Unaxiomatizable logics
After noting that the decidability of
![]() $\mathcal {L}(\{\langle \mathbb {N},\leq \rangle \})$
follows from Büchi’s result (see the previous section), Fine [Reference Fine12, p. 344] asserts that the decidability of
$\mathcal {L}(\{\langle \mathbb {N},\leq \rangle \})$
follows from Büchi’s result (see the previous section), Fine [Reference Fine12, p. 344] asserts that the decidability of
![]() $\mathrm {S4.3}\pi +$
follows from a generalization of Büchi’s result by Rabin [Reference Rabin48]. This, however, is a mistake: Rabin’s result applies to
$\mathrm {S4.3}\pi +$
follows from a generalization of Büchi’s result by Rabin [Reference Rabin48]. This, however, is a mistake: Rabin’s result applies to
![]() $\mathrm {S}k\mathrm {S}$
, for any
$\mathrm {S}k\mathrm {S}$
, for any
![]() $k\in \mathbb {N}\cup \{\omega \}$
, which is the monadic second-order theory of the infinite tree in which every node has exactly k successors. But
$k\in \mathbb {N}\cup \{\omega \}$
, which is the monadic second-order theory of the infinite tree in which every node has exactly k successors. But
![]() $\mathrm {S4.3}$
imposes substantially weaker constraints on frames. For example, any linear order is a relational frame validating
$\mathrm {S4.3}$
imposes substantially weaker constraints on frames. For example, any linear order is a relational frame validating
![]() $\mathrm {S4.3}$
. According to Kaminski and Tiomkin [Reference Kaminski and Tiomkin26, p. 41], it follows from this that
$\mathrm {S4.3}$
. According to Kaminski and Tiomkin [Reference Kaminski and Tiomkin26, p. 41], it follows from this that
![]() $\mathrm {S4.3}\pi +$
is not axiomatizable.
$\mathrm {S4.3}\pi +$
is not axiomatizable.
Kaminski and Tiomkin outline the following argument: Using results of Shelah [Reference Shelah54] and Gurevich and Shelah [Reference Gurevich and Shelah21], second-order arithmetic can be reduced to the monadic second-order theory of linear orders. The monadic second-order theory of linear orders can in turn be reduced to
![]() $\mathrm {S4.3}\pi +$
. (Kaminski and Tiomkin note that under a “weak” set-theoretic assumption, results of Gurevich and Shelah [Reference Gurevich and Shelah20] show that second-order logic can be reduced to the monadic second-order theory of linear orders. Under these assumptions, we therefore obtain that
$\mathrm {S4.3}\pi +$
. (Kaminski and Tiomkin note that under a “weak” set-theoretic assumption, results of Gurevich and Shelah [Reference Gurevich and Shelah20] show that second-order logic can be reduced to the monadic second-order theory of linear orders. Under these assumptions, we therefore obtain that
![]() $\mathrm{S4.3}\pi+$
is not just not axiomatizable, but recursively isomorphic to second-order logic.) In this section, we fill in some details of this observation, and note certain ways in which it can be strengthened.
$\mathrm{S4.3}\pi+$
is not just not axiomatizable, but recursively isomorphic to second-order logic.) In this section, we fill in some details of this observation, and note certain ways in which it can be strengthened.
The reduction of monadic second-order logic over linear orders to
![]() $\mathrm {S4.3}\pi +$
can be effected using the backwards translation, introduced in Section 2.4. The crucial feature of
$\mathrm {S4.3}\pi +$
can be effected using the backwards translation, introduced in Section 2.4. The crucial feature of
![]() $\mathrm {S4.3}$
which makes this possible is the fact that every linear order is a subframe of a transitive point-generated subframe of a frame in
$\mathrm {S4.3}$
which makes this possible is the fact that every linear order is a subframe of a transitive point-generated subframe of a frame in
![]() $\mathsf {R}(\mathrm {S4.3})$
. We therefore present the result in a more general form, applicable to any class of relational frames with this property. Analogous to the results in Section 4, the failure of axiomatizability extends to any smaller set of formulas which includes
$\mathsf {R}(\mathrm {S4.3})$
. We therefore present the result in a more general form, applicable to any class of relational frames with this property. Analogous to the results in Section 4, the failure of axiomatizability extends to any smaller set of formulas which includes
![]() $\mathrm {K}\pi +$
.
$\mathrm {K}\pi +$
.
Proposition 5.10. Let
![]() $\mathsf {C}$
be a class of relational frames such that every linear order is a subframe of a transitive point-generated subframe of a frame in
$\mathsf {C}$
be a class of relational frames such that every linear order is a subframe of a transitive point-generated subframe of a frame in
![]() $\mathsf {C}$
. No set of formulas
$\mathsf {C}$
. No set of formulas
![]() $\Pi \subseteq \mathcal {L}^{\Box }$
such that
$\Pi \subseteq \mathcal {L}^{\Box }$
such that
![]() $\mathrm {K}\pi +\subseteq \Pi \subseteq \mathcal {L}(\mathsf {C})$
is axiomatizable.
$\mathrm {K}\pi +\subseteq \Pi \subseteq \mathcal {L}(\mathsf {C})$
is axiomatizable.
Proof By the results of Shelah and Gurevich mentioned above, it suffices to reduce monadic second-order logic over linear orders to
![]() $\Pi $
. We do so by the function mapping any monadic second-order sentence
$\Pi $
. We do so by the function mapping any monadic second-order sentence
![]() $\varphi $
to
$\varphi $
to
where
![]() $\mathrm {Lin}$
is the (first-order) sentence stating that R is a linear order, and
$\mathrm {Lin}$
is the (first-order) sentence stating that R is a linear order, and
![]() $\psi ^X$
is the restriction of first-order quantifiers in
$\psi ^X$
is the restriction of first-order quantifiers in
![]() $\psi $
to X. We show that
$\psi $
to X. We show that
![]() $\varphi $
is valid over linear orders if and only if
$\varphi $
is valid over linear orders if and only if
![]() $\varphi ^*\in \Pi $
.
$\varphi ^*\in \Pi $
.
Assume
![]() $\varphi $
is false in some linear order. By assumption, the order is a subframe
$\varphi $
is false in some linear order. By assumption, the order is a subframe
![]() $\mathfrak {L}$
of a transitive point-generated subframe
$\mathfrak {L}$
of a transitive point-generated subframe
![]() $\mathfrak {F}_w$
of a frame
$\mathfrak {F}_w$
of a frame
![]() $\mathfrak {F}$
in
$\mathfrak {F}$
in
![]() $\mathsf {C}$
. Then
$\mathsf {C}$
. Then
![]() $\forall X(\mathrm {Lin}\to \varphi )^X$
is false in
$\forall X(\mathrm {Lin}\to \varphi )^X$
is false in
![]() $\mathfrak {F}_w$
. Since
$\mathfrak {F}_w$
. Since
![]() $\mathfrak {F}_w$
is transitive, it follows by Proposition 2.10 that
$\mathfrak {F}_w$
is transitive, it follows by Proposition 2.10 that
![]() $\mathfrak {F}_w,w\nVdash (\forall X(\mathrm {Lin}\to \varphi )^X)^{\leftarrow }$
, and so that
$\mathfrak {F}_w,w\nVdash (\forall X(\mathrm {Lin}\to \varphi )^X)^{\leftarrow }$
, and so that
![]() $\mathfrak {F}_w,w\nVdash \varphi ^*$
. With Proposition 2.7,
$\mathfrak {F}_w,w\nVdash \varphi ^*$
. With Proposition 2.7,
![]() $\varphi ^*\notin \mathcal {L}(\mathsf {C})$
, and so
$\varphi ^*\notin \mathcal {L}(\mathsf {C})$
, and so
![]() $\varphi ^*\notin \Pi $
.
$\varphi ^*\notin \Pi $
.
Assume
![]() $\varphi ^*\notin \Pi $
. Then
$\varphi ^*\notin \Pi $
. Then
![]() $\varphi ^*\notin \mathrm {K}\pi +$
, so there is a relational frame
$\varphi ^*\notin \mathrm {K}\pi +$
, so there is a relational frame
![]() $\mathfrak {F}$
and world w in which
$\mathfrak {F}$
and world w in which
![]() $\bar {\forall }\mathbf {4}$
is true but
$\bar {\forall }\mathbf {4}$
is true but
![]() $(\forall X(\mathrm {Lin}\to \varphi )^X)^{\leftarrow }$
is false (relative to any assignment function). Then
$(\forall X(\mathrm {Lin}\to \varphi )^X)^{\leftarrow }$
is false (relative to any assignment function). Then
![]() $\mathfrak {F}_w$
has a transitive accessibility relation, and so by Propositions 2.7 and 2.10,
$\mathfrak {F}_w$
has a transitive accessibility relation, and so by Propositions 2.7 and 2.10,
![]() $\forall X(\mathrm {Lin}\to \varphi )^X$
is false in
$\forall X(\mathrm {Lin}\to \varphi )^X$
is false in
![]() $\mathfrak {F}_w$
. So there is a (subframe of
$\mathfrak {F}_w$
. So there is a (subframe of
![]() $\mathfrak {F}_w$
which is a) linear order in which
$\mathfrak {F}_w$
which is a) linear order in which
![]() $\varphi $
is false. Therefore
$\varphi $
is false. Therefore
![]() $\varphi $
is not valid over linear orders.
$\varphi $
is not valid over linear orders.
From this result, we can conclude that
![]() $\mathrm {S4.3}\pi +$
is not axiomatizable. This extends to every normal modal logic included in
$\mathrm {S4.3}\pi +$
is not axiomatizable. This extends to every normal modal logic included in
![]() $\mathrm {K3}$
:
$\mathrm {K3}$
:
Example 5.11. For every normal modal logic
![]() $\Lambda \subseteq \mathrm {K3}$
,
$\Lambda \subseteq \mathrm {K3}$
,
![]() $\Lambda \pi +$
is not axiomatizable.
$\Lambda \pi +$
is not axiomatizable.
Proof Let
![]() $\mathfrak {L}$
be a reflexive linear order, and
$\mathfrak {L}$
be a reflexive linear order, and
![]() $\mathfrak {F}$
the result of adding to
$\mathfrak {F}$
the result of adding to
![]() $\mathfrak {L}$
an initial element i and a final element f. Then
$\mathfrak {L}$
an initial element i and a final element f. Then
![]() $\mathfrak {F}$
is a member of
$\mathfrak {F}$
is a member of
![]() $\mathsf {R}(\mathrm {K3})$
, while
$\mathsf {R}(\mathrm {K3})$
, while
![]() $\mathfrak {L}$
is a subframe of
$\mathfrak {L}$
is a subframe of
![]() $\mathfrak {F}_i$
. So,
$\mathfrak {F}_i$
. So,
![]() $\mathsf {R}(\mathrm {K3})$
satisfies the condition of Proposition 5.10, from which the claim follows.
$\mathsf {R}(\mathrm {K3})$
satisfies the condition of Proposition 5.10, from which the claim follows.
6 Multimodal logics
So far, we have considered only examples of unimodal logics. But, as urged already by Scott [Reference Scott and Lambert50, p. 161], applications of modal logics very often require multiple modalities. We therefore turn to the multimodal case. This opens up a vast field of new complexity questions, and we will not attempt as systematic an investigation as we aimed to provide for the unimodal case.
6.1 Fusions
Many interesting multimodal logics can be obtained using general methods for combining unimodal logics. There are different ways of combining modal logics; see [Reference Kurucz, Blackburn, van Benthem and Wolter35] for an introduction. The simplest way of combining two normal modal logics
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Lambda '$
is the formation of their fusion, which is the normal bimodal logic axiomatized by the theorems of
$\Lambda '$
is the formation of their fusion, which is the normal bimodal logic axiomatized by the theorems of
![]() $\Lambda $
for one modality, and those of
$\Lambda $
for one modality, and those of
![]() $\Lambda '$
for the other modality. This definition straightforwardly generalizes to fusions of arbitrary countable sets of normal modal logics. For the following definition, recall that we use
$\Lambda '$
for the other modality. This definition straightforwardly generalizes to fusions of arbitrary countable sets of normal modal logics. For the following definition, recall that we use
![]() $\mathrm {K}$
for the smallest normal modal logic in whatever modal language is contextually salient, which need not be unimodal.
$\mathrm {K}$
for the smallest normal modal logic in whatever modal language is contextually salient, which need not be unimodal.
Definition 6.1. Let I be a countable set, and for each
![]() $i\in I$
, let
$i\in I$
, let
![]() $\Lambda _i\subseteq \mathcal {L}^{\Box _i}$
be a normal unimodal logic. Then the fusion of
$\Lambda _i\subseteq \mathcal {L}^{\Box _i}$
be a normal unimodal logic. Then the fusion of
![]() $\Lambda _i$
(for
$\Lambda _i$
(for
![]() $i\in I$
), written
$i\in I$
), written
![]() $\bigotimes _{i\in I}\Lambda _i$
, is
$\bigotimes _{i\in I}\Lambda _i$
, is
![]() $\mathrm {K}+\bigcup _{i\in I}\Lambda _i$
, the smallest normal modal logic in
$\mathrm {K}+\bigcup _{i\in I}\Lambda _i$
, the smallest normal modal logic in
![]() $\mathcal {L}^{\{\Box _i:i\in I\}}$
including
$\mathcal {L}^{\{\Box _i:i\in I\}}$
including
![]() $\bigcup _{i\in I}\Lambda _i$
.
$\bigcup _{i\in I}\Lambda _i$
.
In the case of combining two logics, we write their fusion as
![]() $\Lambda _1\otimes \Lambda _2$
. When combining unimodal logics, we assume tacitly that they employ distinct modal operators. For example, we simply write
$\Lambda _1\otimes \Lambda _2$
. When combining unimodal logics, we assume tacitly that they employ distinct modal operators. For example, we simply write
![]() $\mathrm {S5}\otimes \mathrm {S5}$
for the fusion of
$\mathrm {S5}\otimes \mathrm {S5}$
for the fusion of
![]() $\mathrm {S5}$
in a unimodal language using different modal operators. We leave the choice of these modal operators unspecified, and choose them according to the relevant context.
$\mathrm {S5}$
in a unimodal language using different modal operators. We leave the choice of these modal operators unspecified, and choose them according to the relevant context.
For our purposes, fusions involving unimodal logics below the axiomatizability boundary in Figure 1 are uninteresting, since the resulting propositionally quantified modal logics will only be axiomatizable in the trivial case in which one of the fused logics is inconsistent (i.e., identical to
![]() $\mathcal {L}^{\Box }$
). This follows from the following observation.
$\mathcal {L}^{\Box }$
). This follows from the following observation.
Proposition 6.2. Let
![]() $\bigotimes _{i\in I}\Lambda _i$
be a fusion of consistent normal unimodal logics. Then for all
$\bigotimes _{i\in I}\Lambda _i$
be a fusion of consistent normal unimodal logics. Then for all
![]() $i\in I$
,
$i\in I$
,
![]() $(\bigotimes _{i\in I}\Lambda _i)\pi +$
is a conservative extension of
$(\bigotimes _{i\in I}\Lambda _i)\pi +$
is a conservative extension of
![]() $\Lambda _i\pi +$
, in the sense that for all
$\Lambda _i\pi +$
, in the sense that for all
![]() $\varphi \in \mathcal {L}^{\Box _i}$
,
$\varphi \in \mathcal {L}^{\Box _i}$
,
![]() $\varphi \in (\bigotimes _{i\in I}\Lambda _i)\pi +$
iff
$\varphi \in (\bigotimes _{i\in I}\Lambda _i)\pi +$
iff
![]() $\varphi \in \Lambda _i\pi +$
.
$\varphi \in \Lambda _i\pi +$
.
Proof Consider any
![]() $i\in I$
, and
$i\in I$
, and
![]() $\mathcal {L}^{\Box _i}$
-formula
$\mathcal {L}^{\Box _i}$
-formula
![]() $\varphi \notin \Lambda _i\pi +$
. Then there is a relational frame
$\varphi \notin \Lambda _i\pi +$
. Then there is a relational frame
![]() $\langle W,R\rangle $
validating
$\langle W,R\rangle $
validating
![]() $\Lambda _i$
but not
$\Lambda _i$
but not
![]() $\varphi $
. As shown by Makinson [Reference Makinson38], any consistent normal unimodal logic is included in either
$\varphi $
. As shown by Makinson [Reference Makinson38], any consistent normal unimodal logic is included in either
![]() $\mathrm {Triv}$
or
$\mathrm {Triv}$
or
![]() $\mathrm {Ver}$
. Let
$\mathrm {Ver}$
. Let
![]() $J=\{j\in I:\Lambda _j\subseteq \mathrm {Triv}\}$
. Let
$J=\{j\in I:\Lambda _j\subseteq \mathrm {Triv}\}$
. Let
![]() $\mathfrak {F}$
be the relational frame
$\mathfrak {F}$
be the relational frame
![]() $\langle W,R_{\Box _j}\rangle _{j\in I}$
such that
$\langle W,R_{\Box _j}\rangle _{j\in I}$
such that
![]() $R_i=R$
,
$R_i=R$
,
![]() $R_j=\mathrm {id}$
for
$R_j=\mathrm {id}$
for
![]() $j\in J$
, and
$j\in J$
, and
![]() $R_j=\emptyset $
in all other cases. Then
$R_j=\emptyset $
in all other cases. Then
![]() $\mathfrak {F}$
validates
$\mathfrak {F}$
validates
![]() $\bigotimes _{i\in I}\Lambda _i$
but not
$\bigotimes _{i\in I}\Lambda _i$
but not
![]() $\varphi $
.
$\varphi $
.
We therefore consider fusions of normal modal logics above the axiomatizability boundary in Figure 1. One such logic has already been considered in the literature on propositionally quantified modal logics: Antonelli and Thomason [Reference Aldo Antonelli and Thomason1] show that
![]() $(\mathrm {S5}\otimes \mathrm {S5})\pi +$
is recursively isomorphic to second-order logic. Proofs of this result can also be found in Kuhn [Reference Kuhn34] and Belardinelli et al. [Reference Belardinelli, van der Hoek and Kuijer2]. Since
$(\mathrm {S5}\otimes \mathrm {S5})\pi +$
is recursively isomorphic to second-order logic. Proofs of this result can also be found in Kuhn [Reference Kuhn34] and Belardinelli et al. [Reference Belardinelli, van der Hoek and Kuijer2]. Since
![]() $\mathrm {S5}$
is already a highly restrictive logic, this indicates that only very rare fusions of unimodal logics define classes of frames whose propositionally quantified modal logics are axiomatizable.
$\mathrm {S5}$
is already a highly restrictive logic, this indicates that only very rare fusions of unimodal logics define classes of frames whose propositionally quantified modal logics are axiomatizable.
One example for such a rare fusion is the finite fusion of normal modal logics of the form
![]() $\mathrm {KAlt}_n$
. For any
$\mathrm {KAlt}_n$
. For any
![]() $n\in \mathbb {N}$
, the unimodal logic
$n\in \mathbb {N}$
, the unimodal logic
![]() $\mathrm {KAlt}_n$
is valid on just those relational frames in which every world can access at most n worlds. Since the satisfiability of a formula with modal depth m is invariant under taking m-step point-generated subframes, the size of frames which need to be considered to determine satisfiability is finitely bounded in terms of m and the indices n of the fused logics.
$\mathrm {KAlt}_n$
is valid on just those relational frames in which every world can access at most n worlds. Since the satisfiability of a formula with modal depth m is invariant under taking m-step point-generated subframes, the size of frames which need to be considered to determine satisfiability is finitely bounded in terms of m and the indices n of the fused logics.
Example 6.3. Let
![]() $I$
be a finite set and,
$I$
be a finite set and,
![]() $n_i\in \mathbb {N}$
for all
$n_i\in \mathbb {N}$
for all
![]() $i\in I$
. Then
$i\in I$
. Then
![]() $(\bigotimes _{i\in I}\mathrm {KAlt}_{n_i})\pi +$
is decidable.
$(\bigotimes _{i\in I}\mathrm {KAlt}_{n_i})\pi +$
is decidable.
Proof Let
![]() $\varphi $
be a formula of modal depth m which is satisfiable on a frame validating
$\varphi $
be a formula of modal depth m which is satisfiable on a frame validating
![]() $(\bigotimes _{i\in I}\Lambda _i)\pi +$
. By Proposition 2.7,
$(\bigotimes _{i\in I}\Lambda _i)\pi +$
. By Proposition 2.7,
![]() $\varphi $
is satisfiable on an m-step-generated subframe, which is bounded in size by
$\varphi $
is satisfiable on an m-step-generated subframe, which is bounded in size by
![]() $\Sigma _{j=0}^m(\Sigma_{i\in I}n_i)^j$
. Decidability follows, since such subframes are recursively enumerable.
$\Sigma _{j=0}^m(\Sigma_{i\in I}n_i)^j$
. Decidability follows, since such subframes are recursively enumerable.
The decidability of
![]() $\mathrm {KAlt}_n\pi +$
follows as a special case; this establishes the last outstanding claim presented in Figure 1. This decidability result in the unimodal case was already noted by ten Cate [Reference ten Cate8, p. 222]. ten Cate also observes that the corresponding monadic second-order theory
$\mathrm {KAlt}_n\pi +$
follows as a special case; this establishes the last outstanding claim presented in Figure 1. This decidability result in the unimodal case was already noted by ten Cate [Reference ten Cate8, p. 222]. ten Cate also observes that the corresponding monadic second-order theory
![]() $\mathcal {M}^{\Box }(\mathrm {KAlt}_n)$
is undecidable as long as
$\mathcal {M}^{\Box }(\mathrm {KAlt}_n)$
is undecidable as long as
![]() $n\geq 2$
. Indeed, it is easy to see that accessibility relations of such frames may serve to encode a pairing function, so that these monadic second-order theories are recursively isomorphic to second-order logic. This highlights that despite the existence of the backwards translation on transitive frames,
$n\geq 2$
. Indeed, it is easy to see that accessibility relations of such frames may serve to encode a pairing function, so that these monadic second-order theories are recursively isomorphic to second-order logic. This highlights that despite the existence of the backwards translation on transitive frames,
![]() $\mathcal {L}^O$
is in general less expressive than
$\mathcal {L}^O$
is in general less expressive than
![]() $\mathcal {M}^O$
. For more on questions of expressivity, see [Reference ten Cate8].
$\mathcal {M}^O$
. For more on questions of expressivity, see [Reference ten Cate8].
6.2 Products and linear fusions
Many applications of multimodal logics require non-trivial interaction axioms between the modalities. For example, consider a combined modal-temporal logic with two modal operators,
![]() $\Box $
for necessary and
$\Box $
for necessary and
![]() $\mathrm {A}$
for always. One might plausibly think that what is necessarily always the case is always necessary, and vice versa. That is, one might include in this modal-temporal logic the principle:
$\mathrm {A}$
for always. One might plausibly think that what is necessarily always the case is always necessary, and vice versa. That is, one might include in this modal-temporal logic the principle:
The particular interaction principles to include in a given multimodal logic will of course depend on the application, but there are some general ways of combining modal logics which lead to non-trivial interaction axioms, and which arise naturally in many contexts.
Continuing with the example of a modal-temporal logic, consider the following simple way of constructing relational frames for such a language: We take a set of alethically possible worlds W as given, as well as a set of times T. The worlds of our frame are pairs of alethically possible worlds and times, i.e., the members of
![]() $W\times T$
. The accessibility relations for the two modalities operate on the respective components of these pairs:
$W\times T$
. The accessibility relations for the two modalities operate on the respective components of these pairs:
![]() $R_{\Box }$
relates pairs with the same time, and
$R_{\Box }$
relates pairs with the same time, and
![]() $R_{\mathrm {A}}$
relates pairs with the same alethically possible world. Such a class of frames for a combined modal-temporal logic was influentially developed by Kaplan [Reference Kaplan, Almog, Perry and Wettstein28]. It is an instance of a very general way of combining unimodal frames into a multimodal frame, and by extension combining normal unimodal logics to a normal multimodal logic. This is known as taking products.
$R_{\mathrm {A}}$
relates pairs with the same alethically possible world. Such a class of frames for a combined modal-temporal logic was influentially developed by Kaplan [Reference Kaplan, Almog, Perry and Wettstein28]. It is an instance of a very general way of combining unimodal frames into a multimodal frame, and by extension combining normal unimodal logics to a normal multimodal logic. This is known as taking products.
Given the results established above, the most natural question concerning the axiomatizability of propositionally quantified modal logic over product frames is whether
![]() $\mathcal {L}(\mathsf {PE})$
is axiomatizable, where
$\mathcal {L}(\mathsf {PE})$
is axiomatizable, where
![]() $\mathsf {PE}$
is the class of products of unimodal relational frames in which the accessibility relation is an equivalence relation. The resulting logic is a strengthening of
$\mathsf {PE}$
is the class of products of unimodal relational frames in which the accessibility relation is an equivalence relation. The resulting logic is a strengthening of
![]() $(\mathrm {S5}\otimes \mathrm {S5})\pi +$
which adds various interaction axioms, including the one stated above for
$(\mathrm {S5}\otimes \mathrm {S5})\pi +$
which adds various interaction axioms, including the one stated above for
![]() $\Box $
and
$\Box $
and
![]() $\mathrm {A}$
. This question is answered by Fritz [Reference Fritz16], who shows that this extension is also recursively isomorphic to second-order logic.
$\mathrm {A}$
. This question is answered by Fritz [Reference Fritz16], who shows that this extension is also recursively isomorphic to second-order logic.
In the case of modal-temporal logics, Montague [Reference Montague, Hintikka, Moravcsik and Suppes39] took a slightly different approach: like Kaplan, he started from a Cartesian product
![]() $W\times T$
, with the same relation for the temporal modality
$W\times T$
, with the same relation for the temporal modality
![]() $\mathrm {A}$
. However, Montague’s accessibility relation for the alethic modality
$\mathrm {A}$
. However, Montague’s accessibility relation for the alethic modality
![]() $\Box $
is universal. More generally, Dorr and Goodman [Reference Dorr and Goodman11] argue that the correct logic of
$\Box $
is universal. More generally, Dorr and Goodman [Reference Dorr and Goodman11] argue that the correct logic of
![]() $\Box $
and
$\Box $
and
![]() $\mathrm {A}$
includes the principle
$\mathrm {A}$
includes the principle
![]() $\Box p\to \mathrm {A}p$
: what is necessary is always the case. On relational frames, this principle is valid just in case
$\Box p\to \mathrm {A}p$
: what is necessary is always the case. On relational frames, this principle is valid just in case
![]() $R_{\mathrm {A}}$
is a subset of
$R_{\mathrm {A}}$
is a subset of
![]() $R_{\Box }$
. Abstracting from Montague’s particular models, this suggests a natural class of frames for our modal-temporal language
$R_{\Box }$
. Abstracting from Montague’s particular models, this suggests a natural class of frames for our modal-temporal language
![]() $\mathcal {L}^{\Box \mathrm {A}}$
, namely the class of bimodal frames in which both accessibility relations are equivalence relations, with
$\mathcal {L}^{\Box \mathrm {A}}$
, namely the class of bimodal frames in which both accessibility relations are equivalence relations, with
![]() $R_{\mathrm {A}}$
being a refinement of
$R_{\mathrm {A}}$
being a refinement of
![]() $R_{\Box }$
. This class is defined by
$R_{\Box }$
. This class is defined by
![]() $\mathrm {S5}\otimes \mathrm {S5}+\Box p\to \mathrm {A}p$
.
$\mathrm {S5}\otimes \mathrm {S5}+\Box p\to \mathrm {A}p$
.
This example suggest a simple general way of combining any two normal unimodal logics
![]() $\Lambda _1$
and
$\Lambda _1$
and
![]() $\Lambda _2$
(in this order), the result of which we call their linear fusion. It is obtained by adding to the fusion of
$\Lambda _2$
(in this order), the result of which we call their linear fusion. It is obtained by adding to the fusion of
![]() $\Lambda _1$
and
$\Lambda _1$
and
![]() $\Lambda _2$
the axiom
$\Lambda _2$
the axiom
![]() $\Box _1p\to \Box _2p$
, where
$\Box _1p\to \Box _2p$
, where
![]() $\Box _1$
and
$\Box _1$
and
![]() $\Box _2$
are the modalities of
$\Box _2$
are the modalities of
![]() $\Lambda _1$
and
$\Lambda _1$
and
![]() $\Lambda _2$
, respectively. This straightforwardly generalizes to any finite sequence of normal modal logics:
$\Lambda _2$
, respectively. This straightforwardly generalizes to any finite sequence of normal modal logics:
Definition 6.4. Let
![]() $\Lambda _0,\dots ,\Lambda _n$
be normal unimodal logics in languages
$\Lambda _0,\dots ,\Lambda _n$
be normal unimodal logics in languages
![]() $\mathcal {L}^{\Box _0},\dots ,\mathcal {L}^{\Box _n}$
, respectively. Then the linear fusion of
$\mathcal {L}^{\Box _0},\dots ,\mathcal {L}^{\Box _n}$
, respectively. Then the linear fusion of
![]() $\Lambda _0,\dots ,\Lambda _n$
is defined as follows:
$\Lambda _0,\dots ,\Lambda _n$
is defined as follows:
We show that in contrast to Kaplan’s product frames, the Montague-inspired approach to modal-temporal logic via linear fusions leads to a decidable propositionally quantified modal logic, as
![]() $(\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5})\pi +$
is decidable. Indeed, this extends to the linear fusion of any finite number of copies of
$(\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5})\pi +$
is decidable. Indeed, this extends to the linear fusion of any finite number of copies of
![]() $\mathrm {S5}$
.
$\mathrm {S5}$
.
Example 6.5.
![]() $(\mathrm {S5}\:\vec {\otimes }\:\cdots \:\vec {\otimes }\:\mathrm {S5})\pi +$
is decidable.
$(\mathrm {S5}\:\vec {\otimes }\:\cdots \:\vec {\otimes }\:\mathrm {S5})\pi +$
is decidable.
Proof We discuss the case of
![]() $(\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5})\pi +$
; it is clear that the argument can be iterated for longer linear fusions. Our main task is to show that
$(\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5})\pi +$
; it is clear that the argument can be iterated for longer linear fusions. Our main task is to show that
![]() $\mathsf {R}(\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5})$
is computably reducible. We do so by showing that it is r-reducible, for
$\mathsf {R}(\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5})$
is computably reducible. We do so by showing that it is r-reducible, for
![]() $r:n\mapsto 2^{(2^{n+1}n)}$
.
$r:n\mapsto 2^{(2^{n+1}n)}$
.
So let
![]() $n\in \mathbb {N}$
, and consider any point-generated subframe
$n\in \mathbb {N}$
, and consider any point-generated subframe
![]() $\mathfrak {F}=\langle W,R_{\Box },R_{\boxtimes }\rangle $
of a frame validating
$\mathfrak {F}=\langle W,R_{\Box },R_{\boxtimes }\rangle $
of a frame validating
![]() $\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5}$
. We use
$\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5}$
. We use
![]() $\mathcal {L}^{\Box \boxtimes }$
as the bimodal language of
$\mathcal {L}^{\Box \boxtimes }$
as the bimodal language of
![]() $\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5}$
, assuming that the latter contains
$\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5}$
, assuming that the latter contains
![]() $\Box p\to \boxtimes p$
.
$\Box p\to \boxtimes p$
.
![]() $\mathfrak {F}$
will be reduced to a finite frame in two stages. First, let
$\mathfrak {F}$
will be reduced to a finite frame in two stages. First, let
![]() $\mathfrak {F}'=\langle W',R^{\prime }_{\Box },R^{\prime }_{\boxtimes }\rangle $
be the frame
$\mathfrak {F}'=\langle W',R^{\prime }_{\Box },R^{\prime }_{\boxtimes }\rangle $
be the frame
![]() $\mathfrak {F}^{2^n}_{\mathrm {id}}$
. By Proposition 3.12,
$\mathfrak {F}^{2^n}_{\mathrm {id}}$
. By Proposition 3.12,
![]() $\mathfrak {F}$
and
$\mathfrak {F}$
and
![]() $\mathfrak {F}'$
are n-equivalent. Second, let
$\mathfrak {F}'$
are n-equivalent. Second, let
![]() $\mathfrak {F}"$
be the frame
$\mathfrak {F}"$
be the frame
![]() $\mathfrak {F}^{\prime 2^{(2^nn)}}_{R^{\prime }_{\boxtimes }}$
. Since the equivalence classes of
$\mathfrak {F}^{\prime 2^{(2^nn)}}_{R^{\prime }_{\boxtimes }}$
. Since the equivalence classes of
![]() $R^{\prime }_{\boxtimes }$
are bounded in size by
$R^{\prime }_{\boxtimes }$
are bounded in size by
![]() $2^n$
, it follows with Proposition 3.12 that
$2^n$
, it follows with Proposition 3.12 that
![]() $\mathfrak {F}'$
and
$\mathfrak {F}'$
and
![]() $\mathfrak {F}"$
are n-equivalent as well.
$\mathfrak {F}"$
are n-equivalent as well.
Since equivalence classes of
![]() $R^{\prime }_{\boxtimes }$
are bounded in size by
$R^{\prime }_{\boxtimes }$
are bounded in size by
![]() $2^n$
, and both
$2^n$
, and both
![]() $R^{\prime }_{\Box }$
and
$R^{\prime }_{\Box }$
and
![]() $R^{\prime }_{\boxtimes }$
are universal within such an equivalence relation, there are only up to
$R^{\prime }_{\boxtimes }$
are universal within such an equivalence relation, there are only up to
![]() $2^n$
duplicate classes of such equivalence classes in
$2^n$
duplicate classes of such equivalence classes in
![]() $\mathfrak {F}'$
. Therefore,
$\mathfrak {F}'$
. Therefore,
![]() $\mathfrak {F}"$
is bounded in size by
$\mathfrak {F}"$
is bounded in size by
![]() $2^n\cdot 2^{(2^nn)}=r(n)$
. By construction, it is easy to see that
$2^n\cdot 2^{(2^nn)}=r(n)$
. By construction, it is easy to see that
![]() $\mathfrak {F}"$
also validates
$\mathfrak {F}"$
also validates
![]() $\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5}$
. Thus
$\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5}$
. Thus
![]() $\mathsf {R}(\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5})$
is r-reducible. Since
$\mathsf {R}(\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5})$
is r-reducible. Since
![]() $\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5}$
is finitely axiomatizable, it follows with Lemma 3.2 that
$\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5}$
is finitely axiomatizable, it follows with Lemma 3.2 that
![]() $(\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5})\pi +$
is decidable.
$(\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5})\pi +$
is decidable.
Along the lines of Example 6.3, it is easy to see that for any linear fusion
![]() $\Lambda =\Lambda _0\:\vec {\otimes }\:\cdots \:\vec {\otimes }\:\Lambda _n$
, if
$\Lambda =\Lambda _0\:\vec {\otimes }\:\cdots \:\vec {\otimes }\:\Lambda _n$
, if
![]() $\Lambda _0$
is
$\Lambda _0$
is
![]() $\mathrm {KAlt}_m$
for some
$\mathrm {KAlt}_m$
for some
![]() $m\in \mathbb {N}$
and every other
$m\in \mathbb {N}$
and every other
![]() $\Lambda _i$
is
$\Lambda _i$
is
![]() $\mathrm {K}\Gamma _i$
for some finite set of axioms
$\mathrm {K}\Gamma _i$
for some finite set of axioms
![]() $\Gamma _i$
, then
$\Gamma _i$
, then
![]() $\Lambda \pi +$
is decidable. However, already
$\Lambda \pi +$
is decidable. However, already
![]() $(\mathrm {S5}\:\vec {\otimes }\:\mathrm {KAlt}_2)\pi +$
is recursively isomorphic to second-order logic. This follows by a straightforward pairing argument, similar to the case of
$(\mathrm {S5}\:\vec {\otimes }\:\mathrm {KAlt}_2)\pi +$
is recursively isomorphic to second-order logic. This follows by a straightforward pairing argument, similar to the case of
![]() $\mathcal {M}^{\Box }(\mathrm {KAlt}_n)$
for
$\mathcal {M}^{\Box }(\mathrm {KAlt}_n)$
for
![]() $n\geq 2$
, discussed above.
$n\geq 2$
, discussed above.
7 Conclusion
In this paper, we have developed general methods to answer questions concerning the axiomatizability of propositionally quantified modal logics on classes of relational frames. Central among these methods is the technique of reducing the number of duplicates of equivalence classes of worlds in relational frames. This led directly to several new decidability results, including the decidability of
![]() $\mathrm {KE}\pi +$
(Example 3.15). The technique can also fruitfully be combined with standard decidability arguments, such as reductions to
$\mathrm {KE}\pi +$
(Example 3.15). The technique can also fruitfully be combined with standard decidability arguments, such as reductions to
![]() $\mathrm {S1S}$
, as we did in order to show that
$\mathrm {S1S}$
, as we did in order to show that
![]() $\mathrm {S4.3.1}\pi +$
is decidable (Example 5.6). Finally, we showed how the reductions of duplicates can be iterated, which allowed us to prove that the multimodal logic
$\mathrm {S4.3.1}\pi +$
is decidable (Example 5.6). Finally, we showed how the reductions of duplicates can be iterated, which allowed us to prove that the multimodal logic
![]() $(\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5})\pi +$
is decidable (Example 6.5). We also improved an existing construction for showing propositionally quantified modal logics of classes of relational frames to be recursively isomorphic to second-order logic. This allowed us to simplify proofs for known cases, and to cover new cases such as
$(\mathrm {S5}\:\vec {\otimes }\:\mathrm {S5})\pi +$
is decidable (Example 6.5). We also improved an existing construction for showing propositionally quantified modal logics of classes of relational frames to be recursively isomorphic to second-order logic. This allowed us to simplify proofs for known cases, and to cover new cases such as
![]() $\mathrm {K4.2W}\pi +$
(Example 4.10).
$\mathrm {K4.2W}\pi +$
(Example 4.10).
The various examples used to illustrate these new and improved methods amount to a detailed picture of which normal unimodal logics define classes of relational frames whose propositionally quantified modal logics are axiomatizable, which is presented in Figure 1. For many of the commonly considered normal modal logics
![]() $\Lambda $
, the complexity of
$\Lambda $
, the complexity of
![]() $\Lambda\pi+$
decreases (weakly) monotonically with the strength of
$\Lambda\pi+$
decreases (weakly) monotonically with the strength of
![]() $\Lambda $
. Among these logics, the question of the axiomatizability of
$\Lambda $
. Among these logics, the question of the axiomatizability of
![]() $\Lambda\pi+$
therefore introduces what Ding [Reference Ding10, p. 1148] calls the “axiomatizability boundary,” which is indicated in Figure 1. This boundary, as well as a corresponding decidability boundary, gives rise to further problems which are left open here.
$\Lambda\pi+$
therefore introduces what Ding [Reference Ding10, p. 1148] calls the “axiomatizability boundary,” which is indicated in Figure 1. This boundary, as well as a corresponding decidability boundary, gives rise to further problems which are left open here.
First, even though we have developed general methods, our approach to locating the axiomatizability boundary has for the most part still been driven by considering particular examples. In some cases, we were able to obtain more general results, such as the observation that
![]() $\Lambda \pi +$
is decidable for every normal extension
$\Lambda \pi +$
is decidable for every normal extension
![]() $\Lambda $
of
$\Lambda $
of
![]() $\mathrm {KE}$
(Corollary 3.16), but much of the lattice of normal modal logics is not covered by any such general result established here.
$\mathrm {KE}$
(Corollary 3.16), but much of the lattice of normal modal logics is not covered by any such general result established here.
Second, one might also take a more abstract perspective on the issue, and ask whether the property of having an axiomatizable propositionally quantified extension
![]() $\Lambda \pi +$
, for axiomatizable normal modal logics
$\Lambda \pi +$
, for axiomatizable normal modal logics
![]() $\Lambda $
, is itself decidable. For an overview of similar complexity questions concerning metalogical properties of modal logics, see [Reference Chagrov and Zakharyaschev9, Chapter 17].
$\Lambda $
, is itself decidable. For an overview of similar complexity questions concerning metalogical properties of modal logics, see [Reference Chagrov and Zakharyaschev9, Chapter 17].
Third, it is not yet clear exactly how much of the lattice of normal modal logics divides neatly along the kind of axiomatizability boundary discussed here. Proposition 2.8 describes a relatively rich space of normal modal logics which does provide such a boundary. However, it follows from Proposition 5.9 that this cannot be extended to all normal modal logics. This limits, but does not pin down exactly, the spaces of normal modal logics to which we may be able to extend the axiomatizability boundary.
Finally, our discussion has been especially unsystematic in the multimodal case. This is partly due to the fact that this case has not been considered in the literature, with the exception of the particular matter of normal bimodal logics in which both unimodal fragments obey the principles of
![]() $\mathrm {S5}$
: It is known that in the case of
$\mathrm {S5}$
: It is known that in the case of
![]() $\mathrm{S5}$
, the two most common methods of combining modal logics, namely fusions and products, both lead to a propositionally quantified bimodal logic which is recursively isomorphic to second-order logic. To this we have added a decidability result, showing that taking the linear fusion of
$\mathrm{S5}$
, the two most common methods of combining modal logics, namely fusions and products, both lead to a propositionally quantified bimodal logic which is recursively isomorphic to second-order logic. To this we have added a decidability result, showing that taking the linear fusion of
![]() $\mathrm{S5}$
with itself leads to a decidable propositionally quantified bimodal logic (Example 6.5). However, many further complexity questions are left open in this area, including many questions on systems with interaction axioms between the modalities motivated by particular applications.
$\mathrm{S5}$
with itself leads to a decidable propositionally quantified bimodal logic (Example 6.5). However, many further complexity questions are left open in this area, including many questions on systems with interaction axioms between the modalities motivated by particular applications.
Acknowledgement
Thanks to Yifeng Ding, Wes Holliday, Johannes Marti, and a referee for this journal for very helpful comments and discussion.