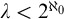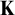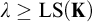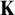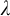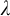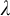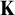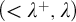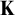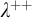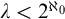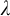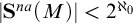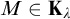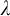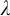1 Introduction
Abstract elementary classes (AECs for short) were introduced by Shelah [Reference Shelah and Baldwin22] to study classes of structures axiomatized in several infinitary logics. Given an abstract elementary class
![]() ${\mathbf {K}}$
and
${\mathbf {K}}$
and
![]() $\lambda $
an infinite cardinal,
$\lambda $
an infinite cardinal,
![]() ${\mathbb {I}}({\mathbf {K}}, \lambda )$
denotes the number of non-isomorphic models in
${\mathbb {I}}({\mathbf {K}}, \lambda )$
denotes the number of non-isomorphic models in
![]() ${\mathbf {K}}$
of cardinality
${\mathbf {K}}$
of cardinality
![]() $\lambda $
. One of the main test questions in the development of abstract elementary classes is Grossberg’s question [Reference Shelah25, Problem (5), p. 34]:Footnote
1
$\lambda $
. One of the main test questions in the development of abstract elementary classes is Grossberg’s question [Reference Shelah25, Problem (5), p. 34]:Footnote
1
Question 1.1. Let
![]() ${\mathbf {K}}$
be an AEC and
${\mathbf {K}}$
be an AEC and
![]() $\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
be an infinite cardinal. If
$\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
be an infinite cardinal. If
![]() ${{\mathbb {I}}({\mathbf {K}}, \lambda )= 1}$
and
${{\mathbb {I}}({\mathbf {K}}, \lambda )= 1}$
and
![]() $1 \leq {\mathbb {I}}({\mathbf {K}}, \lambda ^+) < 2^{\lambda ^+}$
, must
$1 \leq {\mathbb {I}}({\mathbf {K}}, \lambda ^+) < 2^{\lambda ^+}$
, must
![]() ${\mathbf {K}}$
have a model of cardinality
${\mathbf {K}}$
have a model of cardinality
![]() $\lambda ^{++}$
?
$\lambda ^{++}$
?
This question is still open. When the AEC has a countable Löwenheim–Skolem–Tarski number and
![]() $\lambda = \aleph _0$
, the issue of constructing a model in
$\lambda = \aleph _0$
, the issue of constructing a model in
![]() $\aleph _2$
was discussed in Shelah’s pioneering papers [Reference Shelah20, Reference Shelah21] and [Reference Shelah and Baldwin22, Theorem 3.7]. When the AEC has an uncountable Löwenheim–Skolem–Tarski number or
$\aleph _2$
was discussed in Shelah’s pioneering papers [Reference Shelah20, Reference Shelah21] and [Reference Shelah and Baldwin22, Theorem 3.7]. When the AEC has an uncountable Löwenheim–Skolem–Tarski number or
![]() $\lambda> \aleph _0$
Grossberg’s question is known to be significantly harder. For instance, Shelah’s best approximation to Grossberg’s question [Reference Shelah26, Section VI.0(2)], which is a revised version of [Reference Shelah25] published two decades earlier, is over 300 pages long. Additional approximations to Grossberg’s question include [Reference Shelah26, Section II.4.13.3], [Reference Jarden and Shelah11, Proposition 3.1.9], [Reference Vasey29, Theorem 8.9], [Reference Vasey32, Theorem 12.1], [Reference Shelah and Vasey27, Theorem 5.8], [Reference Mazari-Armida and Vasey17, Theorems 3.3 and 4.4], [Reference Mazari-Armida14, Theorem 4.2], [Reference Vasey33, Fact 1.6, Corollary 3.7 and Theorem 5.4], and [Reference Leung13, Remark 4.9].
$\lambda> \aleph _0$
Grossberg’s question is known to be significantly harder. For instance, Shelah’s best approximation to Grossberg’s question [Reference Shelah26, Section VI.0(2)], which is a revised version of [Reference Shelah25] published two decades earlier, is over 300 pages long. Additional approximations to Grossberg’s question include [Reference Shelah26, Section II.4.13.3], [Reference Jarden and Shelah11, Proposition 3.1.9], [Reference Vasey29, Theorem 8.9], [Reference Vasey32, Theorem 12.1], [Reference Shelah and Vasey27, Theorem 5.8], [Reference Mazari-Armida and Vasey17, Theorems 3.3 and 4.4], [Reference Mazari-Armida14, Theorem 4.2], [Reference Vasey33, Fact 1.6, Corollary 3.7 and Theorem 5.4], and [Reference Leung13, Remark 4.9].
A key intermediate step to answer Grossberg’s question has been to show that stability and even the existence of a superstablity-like independence notion follow from categoricity in several cardinals. Recently, there are many results where superstablity-like independence notions, without any categoricity assumptions, have been used to show the existence of larger models [Reference Shelah26, Chapter II.4.13.3], [Reference Jarden and Shelah11, Proposition 3.9], [Reference Vasey29, Theorem 8.9], [Reference Mazari-Armida14, Theorem 4.2]. In this paper, we show that stability, without any categoricity assumptions, is enough to construct larger models for small cardinals assuming a mild locality condition for Galois types.
Theorem 3.14. Suppose
![]() $\lambda <2^{\aleph _0}$
. Let
$\lambda <2^{\aleph _0}$
. Let
![]() ${\mathbf {K}}$
be an abstract elementary class with
${\mathbf {K}}$
be an abstract elementary class with
![]() $\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
. Assume
$\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
. Assume
![]() ${\mathbf {K}}$
has amalgamation in
${\mathbf {K}}$
has amalgamation in
![]() $\lambda $
, no maximal model in
$\lambda $
, no maximal model in
![]() $\lambda $
, and is stable in
$\lambda $
, and is stable in
![]() $\lambda $
. If
$\lambda $
. If
![]() ${\mathbf {K}}$
is
${\mathbf {K}}$
is
![]() $(<\lambda ^+, \lambda )$
-local, then
$(<\lambda ^+, \lambda )$
-local, then
![]() ${\mathbf {K}}$
has a model of cardinality
${\mathbf {K}}$
has a model of cardinality
![]() $\lambda ^{++}$
.
$\lambda ^{++}$
.
To help us compare our results with previous results, let us recall the following three frameworks: universal classes [Reference Shelah and Baldwin23, Reference Tarski28], tame AECs [Reference Grossberg and VanDieren10], and local AECs [Reference Baldwin and Lessmann6, Reference Shelah25]. The first is a semantic assumption on the AEC, while the other two are locality assumptions on Galois types (see Definitions 2.3 and 2.4). The relation between these frameworks is as follows: universal classes are
![]() $(<\aleph _0, \lambda )$
-tame for every
$(<\aleph _0, \lambda )$
-tame for every
![]() $\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
[Reference Vasey30, Theorem 3.7] and
$\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
[Reference Vasey30, Theorem 3.7] and
![]() $(<\aleph _0, \lambda )$
-tame AECs are
$(<\aleph _0, \lambda )$
-tame AECs are
![]() $(<\lambda ^+, \lambda )$
-local for every
$(<\lambda ^+, \lambda )$
-local for every
![]() $\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
. The first inclusion is proper and the second inclusion is not known to be proper (see Question 2.7).
$\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
. The first inclusion is proper and the second inclusion is not known to be proper (see Question 2.7).
When the AEC has an uncountable Löwenheim–Skolem–Tarski number or
![]() $\lambda> \aleph _0$
, Theorem 3.14 is new even for universal classes. When the AEC has a countable Löwenheim–Skolem–Tarski number and
$\lambda> \aleph _0$
, Theorem 3.14 is new even for universal classes. When the AEC has a countable Löwenheim–Skolem–Tarski number and
![]() $\lambda = \aleph _0$
, Theorem 3.14 is new for
$\lambda = \aleph _0$
, Theorem 3.14 is new for
![]() $(\aleph _0, \aleph _0)$
-local AECs. For
$(\aleph _0, \aleph _0)$
-local AECs. For
![]() $(<\aleph _0, \aleph _0)$
-tame AECs Theorem 3.14 can be obtained using [Reference Shelah and Vasey27, Corollary 4.7], [Reference Shelah and Vasey27, Theorem 5.8], and [Reference Shelah26, Conclusion II.4.13],Footnote
2
but the result has never been stated in the literature.
$(<\aleph _0, \aleph _0)$
-tame AECs Theorem 3.14 can be obtained using [Reference Shelah and Vasey27, Corollary 4.7], [Reference Shelah and Vasey27, Theorem 5.8], and [Reference Shelah26, Conclusion II.4.13],Footnote
2
but the result has never been stated in the literature.
A result similar to Theorem 3.14 is [Reference Vasey32, Theorem 12.1]. The main difference is that Vasey’s result has the additional assumption that the AEC is categorical in
![]() $\lambda $
. Moreover, Vasey assumes tameness while we only assume the weaker property of locality for Galois types. It is worth mentioning that Vasey does not assume that
$\lambda $
. Moreover, Vasey assumes tameness while we only assume the weaker property of locality for Galois types. It is worth mentioning that Vasey does not assume that
![]() $\lambda < 2^{\aleph _0}$
, but this is a weak assumption as long as
$\lambda < 2^{\aleph _0}$
, but this is a weak assumption as long as
![]() $\lambda $
is a small cardinal.
$\lambda $
is a small cardinal.
The main difference between the proof of Theorem 3.14 and the previous results is that we focus on finding one good type instead of a family of good types. A good type in this paper is a
![]() $\lambda $
-unique type (see Definition 3.8). Once we have this good type, we carefully build a chain of types above this type to show that every model of cardinality
$\lambda $
-unique type (see Definition 3.8). Once we have this good type, we carefully build a chain of types above this type to show that every model of cardinality
![]() $\lambda ^{+}$
has a proper extension and hence show the existence of a model of cardinality
$\lambda ^{+}$
has a proper extension and hence show the existence of a model of cardinality
![]() $\lambda ^{++}$
.
$\lambda ^{++}$
.
The set theoretic assumption that
![]() $\lambda <2^{\aleph _0}$
and model theoretic assumption of stability in
$\lambda <2^{\aleph _0}$
and model theoretic assumption of stability in
![]() $\lambda $
can be weakened to the model theoretic assumptions that
$\lambda $
can be weakened to the model theoretic assumptions that
![]() $|{\mathbf {S}}^{na}(M)|< 2^{\aleph _0}$
for every
$|{\mathbf {S}}^{na}(M)|< 2^{\aleph _0}$
for every
![]() $M \in {\mathbf {K}}_\lambda $
and stability for
$M \in {\mathbf {K}}_\lambda $
and stability for
![]() $\lambda $
-algebraic types in
$\lambda $
-algebraic types in
![]() $\lambda $
(see Theorem 3.11). The assumption of stability for
$\lambda $
(see Theorem 3.11). The assumption of stability for
![]() $\lambda $
-algebraic types in
$\lambda $
-algebraic types in
![]() $\lambda $
is strictly weaker than stability in
$\lambda $
is strictly weaker than stability in
![]() $\lambda $
as for instance all elementary classes are stable for
$\lambda $
as for instance all elementary classes are stable for
![]() $\lambda $
-algebraic types in
$\lambda $
-algebraic types in
![]() $\lambda $
. Moreover, any AEC with disjoint amalgamation in
$\lambda $
. Moreover, any AEC with disjoint amalgamation in
![]() $\lambda $
is stable for
$\lambda $
is stable for
![]() $\lambda $
-algebraic types in
$\lambda $
-algebraic types in
![]() $\lambda $
(see Proposition 3.3). Due to this, Theorem 3.11 is a significant improvement to Theorem 3.14 as the result holds for some unstable AECs. Theorem 3.11 is new even for universal classes with countable Löwenheim–Skolem–Tarski number and
$\lambda $
(see Proposition 3.3). Due to this, Theorem 3.11 is a significant improvement to Theorem 3.14 as the result holds for some unstable AECs. Theorem 3.11 is new even for universal classes with countable Löwenheim–Skolem–Tarski number and
![]() $\lambda = \aleph _0$
.
$\lambda = \aleph _0$
.
The first version of this paper had an additional section where we presented a positive answer to Grossberg’s question for small cardinals assuming a mild locality condition for Galois types and without any stability assumptions. That result relies on a result of Shelah [Reference Shelah26, Chapter VI.2.11(2)] for which Shelah does not provide an argument, for which the standard argument does not seem to work, and which we were unable to verify. Due to the status of Shelah’s result, following the referee’s advice, we decided not to include that result in the paper, but it can be consulted in [Reference Mazari-Armida and Yang18, Theorem 4.11] and [Reference Yang35].
The paper is organized as follows. Section 2 presents necessary background. Section 3 has the main results.
This paper was written while the second author was working on a Ph.D. thesis under the direction of Rami Grossberg at Carnegie Mellon University, and the second author would like to thank Professor Grossberg for his guidance and assistance in his research in general and in this work specifically. We would like to thank Rami Grossberg for suggesting us to pursue this project and for comments that helped improve the paper. We would also like to thank Sebastien Vasey for many helpful comments that helped improved the paper and for his comments regarding Remark 3.15. We are grateful to the referee for many comments that significantly improved the presentation of the paper, for the equivalence between (2) and (4) of Lemma 3.6 and for Question 3.5.
2 Preliminaries
We assume the reader has some familiarity with abstract elementary classes as presented in [Reference Baldwin1, Sections 4–8], [Reference Grossberg and Zhang9], or [Reference Shelah26, Section 2], but we recall the main notions used in this paper.
An AEC is a pair
![]() ${\mathbf {K}}=(K \le _{{\mathbf {K}}} )$
where K is a class of structures in a fixed language and
${\mathbf {K}}=(K \le _{{\mathbf {K}}} )$
where K is a class of structures in a fixed language and
![]() $\le _{{\mathbf {K}}} $
is a partial order on K extending the substructure relation such that
$\le _{{\mathbf {K}}} $
is a partial order on K extending the substructure relation such that
![]() ${\mathbf {K}}$
is closed under isomorphisms and satisfies the coherence property, the Löwenheim–Skolem–Tarski axiom, and the Tarski–Vaught axioms. The reader can consult the definition in [Reference Baldwin1, Definition 4.1].
${\mathbf {K}}$
is closed under isomorphisms and satisfies the coherence property, the Löwenheim–Skolem–Tarski axiom, and the Tarski–Vaught axioms. The reader can consult the definition in [Reference Baldwin1, Definition 4.1].
Notation 2.1. For any structure M, we denote its universe by
![]() $|M|$
, and its cardinality by
$|M|$
, and its cardinality by
![]() $\|M\|$
. For a cardinal
$\|M\|$
. For a cardinal
![]() $\lambda $
, we let
$\lambda $
, we let
![]() ${\mathbf {K}}_{\lambda }= \{M\in {\mathbf {K}} : \|M\| = \lambda \}$
. When we write
${\mathbf {K}}_{\lambda }= \{M\in {\mathbf {K}} : \|M\| = \lambda \}$
. When we write
![]() $M \le _{{\mathbf {K}}} N$
we assume that
$M \le _{{\mathbf {K}}} N$
we assume that
![]() $M, N \in {\mathbf {K}}$
.
$M, N \in {\mathbf {K}}$
.
For an AEC
![]() ${\mathbf {K}}$
,
${\mathbf {K}}$
,
![]() ${\mathbf {K}}$
has the amalgamation property if for every
${\mathbf {K}}$
has the amalgamation property if for every
![]() $M_0 \le _{{\mathbf {K}}} M_l$
for
$M_0 \le _{{\mathbf {K}}} M_l$
for
![]() $\ell =1,2$
, there is
$\ell =1,2$
, there is
![]() $N\in {\mathbf {K}}$
and
$N\in {\mathbf {K}}$
and
![]() ${\mathbf {K}}$
-embeddings
${\mathbf {K}}$
-embeddings
![]() $f_\ell :M_\ell \to N$
for
$f_\ell :M_\ell \to N$
for
![]() $\ell =1,2$
such that
$\ell =1,2$
such that
![]() $f_1 \restriction _{M_0}=f_2 \restriction _{M_0}$
; and
$f_1 \restriction _{M_0}=f_2 \restriction _{M_0}$
; and
![]() ${\mathbf {K}}$
has no maximal models if every
${\mathbf {K}}$
has no maximal models if every
![]() $M\in {\mathbf {K}}$
has a proper
$M\in {\mathbf {K}}$
has a proper
![]() $\le _{{\mathbf {K}}} $
-extension in
$\le _{{\mathbf {K}}} $
-extension in
![]() ${\mathbf {K}}$
. For a property P, we say that
${\mathbf {K}}$
. For a property P, we say that
![]() ${\mathbf {K}}$
has P in
${\mathbf {K}}$
has P in
![]() $\lambda $
if
$\lambda $
if
![]() ${\mathbf {K}}_\lambda $
has the property P.
${\mathbf {K}}_\lambda $
has the property P.
Throughout the rest of this section
![]() ${\mathbf {K}}$
is always an abstract elementary class and
${\mathbf {K}}$
is always an abstract elementary class and
![]() $\lambda $
is always a cardinal greater than or equal to the Löwenheim–Skolem–Tarski number of
$\lambda $
is always a cardinal greater than or equal to the Löwenheim–Skolem–Tarski number of
![]() ${\mathbf {K}}$
.
${\mathbf {K}}$
.
We recall the notion of a Galois type. These were originally introduced by Shelah.
Definition 2.2.
-
(1) For
 $(b_1, A_1, N_1), (b_2, A_2, N_2)$
such that
$(b_1, A_1, N_1), (b_2, A_2, N_2)$
such that
 $N_\ell \in {\mathbf {K}}$
,
$N_\ell \in {\mathbf {K}}$
,
 $A_\ell \subseteq |N|$
and
$A_\ell \subseteq |N|$
and
 $b_\ell \in N_\ell $
for
$b_\ell \in N_\ell $
for
 $\ell =1, 2$
,
$\ell =1, 2$
,
 $(b_1, A_1, N_1)E_{\text {at}} (b_2, A_2, N_2)$
if
$(b_1, A_1, N_1)E_{\text {at}} (b_2, A_2, N_2)$
if
 $A := A_1 = A_2$
, and there exist
$A := A_1 = A_2$
, and there exist
 ${\mathbf {K}}$
-embeddings
${\mathbf {K}}$
-embeddings
 $f_\ell : N_\ell \to N$
for
$f_\ell : N_\ell \to N$
for
 $\ell = 1, 2$
such that
$\ell = 1, 2$
such that
 $f_1 (b_1) = f_2 (b_2)$
and
$f_1 (b_1) = f_2 (b_2)$
and
 $f_1\restriction _{A}=f_2\restriction _A$
. Let E be the transitive closure of
$f_1\restriction _{A}=f_2\restriction _A$
. Let E be the transitive closure of
 $E_{\text {at}}$
.
$E_{\text {at}}$
. -
(2) Given
 $(b, A, N)$
, where
$(b, A, N)$
, where
 $N \in {\mathbf {K}}$
,
$N \in {\mathbf {K}}$
,
 $A \subseteq |N|$
, and
$A \subseteq |N|$
, and
 $b\in N$
, the Galois type of b over A in N, denoted by
$b\in N$
, the Galois type of b over A in N, denoted by
 ${\mathbf {gtp}} (b/A, N)$
, is the equivalence class of
${\mathbf {gtp}} (b/A, N)$
, is the equivalence class of
 $(b, A, N)$
modulo E.
$(b, A, N)$
modulo E. -
(3) For
 $M\in {\mathbf {K}}$
,
$M\in {\mathbf {K}}$
,
 ${\mathbf {S}}(M):=\{{\mathbf {gtp}}(a/M,N): M \le _{{\mathbf {K}}} N \text { and } a \in |N| \}$
denotes the set of all Galois types over M and
${\mathbf {S}}(M):=\{{\mathbf {gtp}}(a/M,N): M \le _{{\mathbf {K}}} N \text { and } a \in |N| \}$
denotes the set of all Galois types over M and
 ${\mathbf {S}}^{na}(M):=\{{\mathbf {gtp}}(a/M,N): M \le _{{\mathbf {K}}} N \text { and } a \in |N| \backslash |M| \}$
denotes the set of all non-algebraic types over M.
${\mathbf {S}}^{na}(M):=\{{\mathbf {gtp}}(a/M,N): M \le _{{\mathbf {K}}} N \text { and } a \in |N| \backslash |M| \}$
denotes the set of all non-algebraic types over M. -
(4) Given
 $p={\mathbf {gtp}}(b/A, N)$
and
$p={\mathbf {gtp}}(b/A, N)$
and
 $C \subseteq A$
, let
$C \subseteq A$
, let
 $p\upharpoonright {C}= [(b, C, N)]_{E}$
. Given
$p\upharpoonright {C}= [(b, C, N)]_{E}$
. Given
 $M \le _{{\mathbf {K}}} N$
,
$M \le _{{\mathbf {K}}} N$
,
 $p \in {\mathbf {S}}(N)$
and
$p \in {\mathbf {S}}(N)$
and
 $q \in {\mathbf {S}}(M)$
, p extends q, denoted by
$q \in {\mathbf {S}}(M)$
, p extends q, denoted by
 $q \leq p$
, if
$q \leq p$
, if
 $p\restriction _M = q$
.
$p\restriction _M = q$
.
Tameness and locality are properties asserting that distinct Galois types are witnessed locally. Tameness appears in some of the arguments of [Reference Shelah24] and was isolated in [Reference Grossberg and VanDieren10]. Locality appears for the first time in-print in [Reference Shelah25].
Definition 2.3.
-
(1)
 ${\mathbf {K}}$
is
${\mathbf {K}}$
is
 $(\kappa ,\lambda )$
-tame if for every
$(\kappa ,\lambda )$
-tame if for every
 $M \in {\mathbf {K}}_\lambda $
and every
$M \in {\mathbf {K}}_\lambda $
and every
 $p,q\in {\mathbf {S}}(M)$
, if
$p,q\in {\mathbf {S}}(M)$
, if
 $p\neq q$
, then there is
$p\neq q$
, then there is
 $A \subseteq |M|$
of cardinality
$A \subseteq |M|$
of cardinality
 $\kappa $
such that
$\kappa $
such that
 $p\restriction _A \neq q\restriction _A$
.
$p\restriction _A \neq q\restriction _A$
. -
(2)
 ${\mathbf {K}}$
is
${\mathbf {K}}$
is
 $(< \kappa , \lambda )$
-tame if for every
$(< \kappa , \lambda )$
-tame if for every
 $M \in {\mathbf {K}}_\lambda $
and every
$M \in {\mathbf {K}}_\lambda $
and every
 $p,q\in {\mathbf {S}}(M)$
, if
$p,q\in {\mathbf {S}}(M)$
, if
 $p\neq q$
, then there is
$p\neq q$
, then there is
 $A \subseteq |M|$
of cardinality less than
$A \subseteq |M|$
of cardinality less than
 $\kappa $
such that
$\kappa $
such that
 $p\restriction _A \neq q\restriction _A$
.
$p\restriction _A \neq q\restriction _A$
.
Definition 2.4.
-
(1)
 ${\mathbf {K}}$
is
${\mathbf {K}}$
is
 $(\kappa ,\lambda )$
-local if for every
$(\kappa ,\lambda )$
-local if for every
 $M \in {\mathbf {K}}_\lambda $
, every increasing continuous chain
$M \in {\mathbf {K}}_\lambda $
, every increasing continuous chain
 $\langle M_i : i<\kappa \rangle $
such that
$\langle M_i : i<\kappa \rangle $
such that
 $M=\bigcup _{i<\kappa }M_i$
and every
$M=\bigcup _{i<\kappa }M_i$
and every
 $p,q\in {\mathbf {S}}(M)$
, if
$p,q\in {\mathbf {S}}(M)$
, if
 $p\restriction _{M_i}=q\restriction _{M_i}$
for all
$p\restriction _{M_i}=q\restriction _{M_i}$
for all
 $i < \kappa $
then
$i < \kappa $
then
 $p=q$
.
$p=q$
. -
(2)
 ${\mathbf {K}}$
is
${\mathbf {K}}$
is
 $(< \kappa , \lambda )$
-local if
$(< \kappa , \lambda )$
-local if
 ${\mathbf {K}}$
is
${\mathbf {K}}$
is
 $(\mu ,\lambda )$
-local for all
$(\mu ,\lambda )$
-local for all
 $\mu <\kappa $
.
$\mu <\kappa $
.
Below are some relations between tameness and locality.
Proposition 2.5. Let
![]() $\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
.
$\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
.
-
(1) If
 ${\mathbf {K}}$
is
${\mathbf {K}}$
is
 $(< \aleph _0, \lambda )$
-tame, then
$(< \aleph _0, \lambda )$
-tame, then
 ${\mathbf {K}}$
is
${\mathbf {K}}$
is
 $(< \lambda ^+, \lambda )$
-local.
$(< \lambda ^+, \lambda )$
-local. -
(2) Assume
 $\lambda> {\operatorname {LS}}({\mathbf {K}})$
. If
$\lambda> {\operatorname {LS}}({\mathbf {K}})$
. If
 ${\mathbf {K}}$
is
${\mathbf {K}}$
is
 $( \lambda , \lambda )$
-local, then
$( \lambda , \lambda )$
-local, then
 ${\mathbf {K}}$
is
${\mathbf {K}}$
is
 $(<\lambda , \lambda )$
-tame.
$(<\lambda , \lambda )$
-tame. -
(3) If
 ${\mathbf {K}}$
is
${\mathbf {K}}$
is
 $( \mu , \mu )$
-local for every
$( \mu , \mu )$
-local for every
 $\mu \leq \lambda $
, then
$\mu \leq \lambda $
, then
 ${\mathbf {K}}$
is
${\mathbf {K}}$
is
 $({\operatorname {LS}}({\mathbf {K}}), \mu )$
-tame for every
$({\operatorname {LS}}({\mathbf {K}}), \mu )$
-tame for every
 $\mu \leq \lambda $
.
$\mu \leq \lambda $
. -
(4) Assume
 $\lambda \geq \kappa $
,
$\lambda \geq \kappa $
,
 ${\text {cf }} (\kappa )>\chi $
. If
${\text {cf }} (\kappa )>\chi $
. If
 ${\mathbf {K}}$
is
${\mathbf {K}}$
is
 $(\chi ,\lambda )$
-tame, then
$(\chi ,\lambda )$
-tame, then
 ${\mathbf {K}}$
is
${\mathbf {K}}$
is
 $(\kappa ,\lambda )$
-local.
$(\kappa ,\lambda )$
-local.
Proof
-
(1) Straightforward.
-
(2) Let
 $M \in {\mathbf {K}}_\lambda $
and
$M \in {\mathbf {K}}_\lambda $
and
 $p, q \in {\mathbf {S}} (M)$
such that
$p, q \in {\mathbf {S}} (M)$
such that
 $p\restriction _A = q\restriction _A$
for every
$p\restriction _A = q\restriction _A$
for every
 $A \subseteq |M|$
with
$A \subseteq |M|$
with
 $|A| < \lambda $
. Let
$|A| < \lambda $
. Let
 $\langle M_i : i < \lambda \rangle $
be an increasing continuous chain such that
$\langle M_i : i < \lambda \rangle $
be an increasing continuous chain such that
 $M=\bigcup _{i<\lambda }M_i$
and
$M=\bigcup _{i<\lambda }M_i$
and
 $\| M_i \| \leq {\operatorname {LS}}({\mathbf {K}}) + |i|$
for every
$\| M_i \| \leq {\operatorname {LS}}({\mathbf {K}}) + |i|$
for every
 $i < \lambda $
. Since
$i < \lambda $
. Since
 $\|M_i\| < \lambda $
for every
$\|M_i\| < \lambda $
for every
 $i < \lambda $
,
$i < \lambda $
,
 $p\restriction _{M_i} = q\restriction _{M_i}$
for every
$p\restriction _{M_i} = q\restriction _{M_i}$
for every
 $i < \lambda $
. Therefore,
$i < \lambda $
. Therefore,
 $p = q$
as
$p = q$
as
 ${\mathbf {K}}$
is
${\mathbf {K}}$
is
 $(\lambda , \lambda )$
-local.
$(\lambda , \lambda )$
-local. -
(3) Similar to (2), see also [Reference Baldwin and Lessmann6, Proposition 1.18].
-
(4) This is [Reference Baldwin and Shelah7, Lemma 1.11]
Remark 2.6. Universal classes are
![]() $(<\aleph _0, \lambda )$
-tame for every
$(<\aleph _0, \lambda )$
-tame for every
![]() $\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
[Reference Vasey30, Theorem 3.7], Quasiminimal AECs (in the sense of [Reference Vasey31]) are
$\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
[Reference Vasey30, Theorem 3.7], Quasiminimal AECs (in the sense of [Reference Vasey31]) are
![]() $(<\aleph _0, \lambda )$
-tame for every
$(<\aleph _0, \lambda )$
-tame for every
![]() $\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
[Reference Vasey31, Corollary 4.18], and many natural AECs of modules are
$\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
[Reference Vasey31, Corollary 4.18], and many natural AECs of modules are
![]() $(<\aleph _0, \lambda )$
-tame for every
$(<\aleph _0, \lambda )$
-tame for every
![]() $\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
(see, for example, [Reference Mazari-Armida15, Section 3]). The main results of this paper assume that the AEC is
$\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
(see, for example, [Reference Mazari-Armida15, Section 3]). The main results of this paper assume that the AEC is
![]() $(<\lambda ^+, \lambda )$
-local, so they apply to all of these classes.
$(<\lambda ^+, \lambda )$
-local, so they apply to all of these classes.
On the other hand there are AECs which are not
![]() $(\aleph _1, \aleph _1)$
-local [Reference Baldwin and Shelah7] and which are not tame [Reference Baldwin and Kolesnikov4].
$(\aleph _1, \aleph _1)$
-local [Reference Baldwin and Shelah7] and which are not tame [Reference Baldwin and Kolesnikov4].
A natural question we were unable to answer is the following:
Question 2.7. If
![]() ${\mathbf {K}}$
is
${\mathbf {K}}$
is
![]() $( \aleph _0, \aleph _0)$
-local, is
$( \aleph _0, \aleph _0)$
-local, is
![]() ${\mathbf {K}} (< \aleph _0, \aleph _0)$
-tame?
${\mathbf {K}} (< \aleph _0, \aleph _0)$
-tame?
Recall that if
![]() $\langle M_i : i<\omega \rangle $
is an increasing chain, then any increasing sequence of types
$\langle M_i : i<\omega \rangle $
is an increasing chain, then any increasing sequence of types
![]() $\langle p_i\in {\mathbf {S}}(M_i) : i<\omega \rangle $
has an upper bound. For longer sequences of types an upper bound might not exist. A sufficient condition for a sequence to have an upper bounds is coherence (see, for example, [Reference Mazari-Armida14, Definition 3.14] for the definition).
$\langle p_i\in {\mathbf {S}}(M_i) : i<\omega \rangle $
has an upper bound. For longer sequences of types an upper bound might not exist. A sufficient condition for a sequence to have an upper bounds is coherence (see, for example, [Reference Mazari-Armida14, Definition 3.14] for the definition).
Fact 2.8. Let
![]() $\delta $
be a limit ordinal and
$\delta $
be a limit ordinal and
![]() $\langle M_i : i\leq \delta \rangle $
be an increasing continuous chain. If
$\langle M_i : i\leq \delta \rangle $
be an increasing continuous chain. If
![]() $\langle p_i\in {\mathbf {S}}^{na}(M_i) : i<\delta \rangle $
is a coherent sequence of types, then there is
$\langle p_i\in {\mathbf {S}}^{na}(M_i) : i<\delta \rangle $
is a coherent sequence of types, then there is
![]() $p\in {\mathbf {S}}^{na}(M_\delta )$
such that
$p\in {\mathbf {S}}^{na}(M_\delta )$
such that
![]() $p \geq p_i$
for every
$p \geq p_i$
for every
![]() $i < \delta $
and
$i < \delta $
and
![]() $\langle p_i\in {\mathbf {S}}^{na}(M_i) : i < \delta + 1\rangle $
is coherent.
$\langle p_i\in {\mathbf {S}}^{na}(M_i) : i < \delta + 1\rangle $
is coherent.
3 Main results
In this section we prove the main results of the paper. Throughout this section
![]() ${\mathbf {K}}$
is always an abstract elementary class and
${\mathbf {K}}$
is always an abstract elementary class and
![]() $\lambda $
is always a cardinal greater than or equal to the Löwenheim–Skolem–Tarski number of
$\lambda $
is always a cardinal greater than or equal to the Löwenheim–Skolem–Tarski number of
![]() ${\mathbf {K}}$
. We begin by recalling the following notions that appear in [Reference Yang34] and [Reference Shelah26, Section VI].
${\mathbf {K}}$
. We begin by recalling the following notions that appear in [Reference Yang34] and [Reference Shelah26, Section VI].
Definition 3.1.
-
•
 $p={\mathbf {gtp}}(a/M,N)$
has the
$p={\mathbf {gtp}}(a/M,N)$
has the
 $\lambda $
-extension property if for every
$\lambda $
-extension property if for every
 $M'\in {\mathbf {K}}_\lambda \le _{{\mathbf {K}}} $
-extending M, there is
$M'\in {\mathbf {K}}_\lambda \le _{{\mathbf {K}}} $
-extending M, there is
 $q\in {\mathbf {S}}^{na}(M')$
extending p. In this case we say
$q\in {\mathbf {S}}^{na}(M')$
extending p. In this case we say
 $p\in {\mathbf {S}}^{\lambda -ext}(M)$
.Footnote
3
$p\in {\mathbf {S}}^{\lambda -ext}(M)$
.Footnote
3
-
•
 $p={\mathbf {gtp}}(a/M,N)$
is
$p={\mathbf {gtp}}(a/M,N)$
is
 $\lambda $
-algebraic if
$\lambda $
-algebraic if
 $p \in {\mathbf {S}}^{na}(M)-{\mathbf {S}}^{\lambda -ext}(M)$
. Let
$p \in {\mathbf {S}}^{na}(M)-{\mathbf {S}}^{\lambda -ext}(M)$
. Let
 ${\mathbf {S}}^{\lambda -al}(M)$
denote the
${\mathbf {S}}^{\lambda -al}(M)$
denote the
 $\lambda $
-algebraic types over M.
$\lambda $
-algebraic types over M.
Observe that if p has the
![]() $\lambda $
-extension property and
$\lambda $
-extension property and
![]() $dom(p) \in {\mathbf {K}}_\lambda $
then p is non-algebraic.
$dom(p) \in {\mathbf {K}}_\lambda $
then p is non-algebraic.
Recall that an AEC
![]() ${\mathbf {K}}$
is stable in
${\mathbf {K}}$
is stable in
![]() $\lambda $
if
$\lambda $
if
![]() $| {\mathbf {S}}(M)| \leq \lambda $
for every
$| {\mathbf {S}}(M)| \leq \lambda $
for every
![]() $M \in {\mathbf {K}}_\lambda $
. We introduce a weakening of stability.
$M \in {\mathbf {K}}_\lambda $
. We introduce a weakening of stability.
Definition 3.2.
![]() ${\mathbf {K}}$
is stable for
${\mathbf {K}}$
is stable for
![]() $\lambda $
-algebraic types in
$\lambda $
-algebraic types in
![]() $\lambda $
if for all
$\lambda $
if for all
![]() $M\in {\mathbf {K}}_\lambda $
,
$M\in {\mathbf {K}}_\lambda $
,
![]() $|{\mathbf {S}}^{\lambda -al}(M)|\leq \lambda $
.
$|{\mathbf {S}}^{\lambda -al}(M)|\leq \lambda $
.
Recall that an AEC
![]() ${\mathbf {K}}$
has disjoint amalgamation in
${\mathbf {K}}$
has disjoint amalgamation in
![]() $\lambda $
if for any
$\lambda $
if for any
![]() $M, N_1, N_2 \in {\mathbf {K}}_\lambda $
, if
$M, N_1, N_2 \in {\mathbf {K}}_\lambda $
, if
![]() $M \le _{{\mathbf {K}}} N_1, N_2$
and
$M \le _{{\mathbf {K}}} N_1, N_2$
and
![]() $N_1 \cap N_2 = M$
then there are
$N_1 \cap N_2 = M$
then there are
![]() $N \in {\mathbf {K}}_\lambda $
,
$N \in {\mathbf {K}}_\lambda $
,
![]() $f_1: N_1 \to N$
, and
$f_1: N_1 \to N$
, and
![]() $f_2: N_2 \to N$
such that
$f_2: N_2 \to N$
such that
![]() $f_1\upharpoonright _M= f_2 \upharpoonright _M$
and
$f_1\upharpoonright _M= f_2 \upharpoonright _M$
and
![]() $f_1[N_1] \cap f_2[N_2] = f_1[M](= f_2[M])$
. There are many AECs with disjoint amalgamation (see, for example, [Reference Baldwin, Eklof and Trlifaj2, Remark 2.2], [Reference Baldwin, Kolesnikov and Shelah5], [Reference Baldwin, Koerwien and Laskowski3], and [Reference Mazari-Armida and Rosicky16, Remark 2.10]).
$f_1[N_1] \cap f_2[N_2] = f_1[M](= f_2[M])$
. There are many AECs with disjoint amalgamation (see, for example, [Reference Baldwin, Eklof and Trlifaj2, Remark 2.2], [Reference Baldwin, Kolesnikov and Shelah5], [Reference Baldwin, Koerwien and Laskowski3], and [Reference Mazari-Armida and Rosicky16, Remark 2.10]).
Proposition 3.3. If
![]() $\kern2pt{\mathbf {K}}$
has disjoint amalgamation in
$\kern2pt{\mathbf {K}}$
has disjoint amalgamation in
![]() $\lambda $
, then
$\lambda $
, then
![]() ${\mathbf {S}}^{\lambda -al}(M) = \emptyset $
for every
${\mathbf {S}}^{\lambda -al}(M) = \emptyset $
for every
![]() $M \in {\mathbf {K}}_\lambda $
. In particular,
$M \in {\mathbf {K}}_\lambda $
. In particular,
![]() ${\mathbf {K}}$
is stable for
${\mathbf {K}}$
is stable for
![]() $\lambda $
-algebraic types in
$\lambda $
-algebraic types in
![]() $\lambda $
.
$\lambda $
.
Proof Let
![]() $M \in {\mathbf {K}}_\lambda $
. Suppose
$M \in {\mathbf {K}}_\lambda $
. Suppose
![]() $p={\mathbf {gtp}}(a/M,N)$
for
$p={\mathbf {gtp}}(a/M,N)$
for
![]() $a\in |N|-|M|$
. Let
$a\in |N|-|M|$
. Let
![]() $M' \in {\mathbf {K}}_\lambda $
with
$M' \in {\mathbf {K}}_\lambda $
with
![]() $M'\geq _{\mathbf {K}} M$
. Let
$M'\geq _{\mathbf {K}} M$
. Let
![]() $M" \in {\mathbf {K}}_\lambda $
and
$M" \in {\mathbf {K}}_\lambda $
and
![]() $f: M' \cong M"$
such that
$f: M' \cong M"$
such that
![]() $M" \cap N = M$
,
$M" \cap N = M$
,
![]() $M\le _{{\mathbf {K}}} M"$
, and
$M\le _{{\mathbf {K}}} M"$
, and
![]() $f\upharpoonright _M= id_M$
. Amalgamate
$f\upharpoonright _M= id_M$
. Amalgamate
![]() $M \le _{{\mathbf {K}}} M", N$
such that for some g the following commutes:
$M \le _{{\mathbf {K}}} M", N$
such that for some g the following commutes:

and
![]() $g[N]\cap M"=M$
. This is possible by disjoint amalgamation in
$g[N]\cap M"=M$
. This is possible by disjoint amalgamation in
![]() $\lambda $
.
$\lambda $
.
Let
![]() $L' \in {\mathbf {K}}_\lambda $
and
$L' \in {\mathbf {K}}_\lambda $
and
![]() $h: L' \cong L$
such that
$h: L' \cong L$
such that
![]() $M' \le _{{\mathbf {K}}} L'$
and
$M' \le _{{\mathbf {K}}} L'$
and
![]() $h\upharpoonright _{M'} = f\upharpoonright _{M'}$
.
$h\upharpoonright _{M'} = f\upharpoonright _{M'}$
.
Let
![]() $q= {\mathbf {gtp}}(h^{-1}(g(a))/M', L')$
. It is straightforward to show that q extends p and q is a non-algebraic type because
$q= {\mathbf {gtp}}(h^{-1}(g(a))/M', L')$
. It is straightforward to show that q extends p and q is a non-algebraic type because
![]() $g(a) \notin |M"|$
as
$g(a) \notin |M"|$
as
![]() $g[N]\cap M"=M$
.
$g[N]\cap M"=M$
.
Remark 3.4. The previous result shows that stability for
![]() $\lambda $
-algebraic types in
$\lambda $
-algebraic types in
![]() $\lambda $
is strictly weaker than stability in
$\lambda $
is strictly weaker than stability in
![]() $\lambda $
as AECs axiomatizable by a complete first-order theory have disjoint amalgamation (in all cardinals).
$\lambda $
as AECs axiomatizable by a complete first-order theory have disjoint amalgamation (in all cardinals).
A natural question, suggested by the referee, we were unable to answer is the following:
Question 3.5. Find a (natural) example of an AEC that is stable for
![]() $\lambda $
-algebraic types in
$\lambda $
-algebraic types in
![]() $\lambda $
but such that
$\lambda $
but such that
![]() ${\mathbf {S}}^{\lambda -al}(M) \neq \emptyset $
for some
${\mathbf {S}}^{\lambda -al}(M) \neq \emptyset $
for some
![]() $M \in {\mathbf {K}}_\lambda $
.
$M \in {\mathbf {K}}_\lambda $
.
We begin working towards proving the main results of the paper.
Lemma 3.6. Assume that
![]() ${\mathbf {K}}$
has amalgamation in
${\mathbf {K}}$
has amalgamation in
![]() $\lambda $
, no maximal model in
$\lambda $
, no maximal model in
![]() $\lambda $
, and is stable for
$\lambda $
, and is stable for
![]() $\lambda $
-algebraic types in
$\lambda $
-algebraic types in
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $p \in {\mathbf {S}}(M)$
and
$p \in {\mathbf {S}}(M)$
and
![]() $M \in {\mathbf {K}}_\lambda $
. The following are equivalent.
$M \in {\mathbf {K}}_\lambda $
. The following are equivalent.
-
(1) p has the
 $\lambda $
-extension property.
$\lambda $
-extension property. -
(2) p has
 $\geq \lambda ^+$
realizations in some
$\geq \lambda ^+$
realizations in some
 $M' \in {\mathbf {K}}$
such that
$M' \in {\mathbf {K}}$
such that
 $M \le _{{\mathbf {K}}} M'$
.
$M \le _{{\mathbf {K}}} M'$
.
Moreover if
![]() ${\mathbf {K}}$
is stable for
${\mathbf {K}}$
is stable for
![]() $\lambda $
-algebraic types in
$\lambda $
-algebraic types in
![]() $\lambda $
, the conditions above are equivalent to:
$\lambda $
, the conditions above are equivalent to:
-
(3) p has an extension to a type with the
 $\lambda $
-extension property for every
$\lambda $
-extension property for every
 $M' \in {\mathbf {K}}_\lambda $
a
$M' \in {\mathbf {K}}_\lambda $
a
 $\le _{{\mathbf {K}}} $
-extension of M.
$\le _{{\mathbf {K}}} $
-extension of M.
Moreover if
![]() ${\mathbf {K}}$
is stable in
${\mathbf {K}}$
is stable in
![]() $\lambda $
, the conditions above are equivalent to:
$\lambda $
, the conditions above are equivalent to:
-
(4) p has an extension to a non-algebraic type to some
 $M'$
universal extension of M.Footnote
4
$M'$
universal extension of M.Footnote
4
Proof The equivalence between (1) and (2) appears in [Reference Shelah25, Claim 2.9] (see also [Reference Baldwin and Lessmann6, Proposition 2.2]).
Assume
![]() ${\mathbf {K}}$
is stable for
${\mathbf {K}}$
is stable for
![]() $\lambda $
-algebraic types in
$\lambda $
-algebraic types in
![]() $\lambda $
. (3) implies (1) is clear, so we only need to show (2) implies (3).
$\lambda $
. (3) implies (1) is clear, so we only need to show (2) implies (3).
Let
![]() $M' \in {\mathbf {K}}_\lambda $
with
$M' \in {\mathbf {K}}_\lambda $
with
![]() $M \le _{{\mathbf {K}}} M'$
. By (2) there are
$M \le _{{\mathbf {K}}} M'$
. By (2) there are
![]() $N \geq _{\mathbf {K}} M$
and
$N \geq _{\mathbf {K}} M$
and
![]() $\{a_i\in |N| : i<\lambda ^+\}$
distinct realizations of
$\{a_i\in |N| : i<\lambda ^+\}$
distinct realizations of
![]() $p:= {\mathbf {gtp}}(a/M, N)$
. Using amalgamation in
$p:= {\mathbf {gtp}}(a/M, N)$
. Using amalgamation in
![]() $\lambda $
we may assume that
$\lambda $
we may assume that
![]() $M' \le _{{\mathbf {K}}} N$
. Moreover, we may assume without loss of generality that for all
$M' \le _{{\mathbf {K}}} N$
. Moreover, we may assume without loss of generality that for all
![]() $i<\lambda ^+$
,
$i<\lambda ^+$
,
![]() $a_i\notin |M'|$
. If not, subtract those
$a_i\notin |M'|$
. If not, subtract those
![]() $a_i$
that are in
$a_i$
that are in
![]() $M'$
. Observe that
$M'$
. Observe that
![]() ${\mathbf {gtp}}(a_i/M',N)\geq p$
and
${\mathbf {gtp}}(a_i/M',N)\geq p$
and
![]() ${\mathbf {gtp}}(a_i/M',N) \in {\mathbf {S}}^{na}(M')$
for all
${\mathbf {gtp}}(a_i/M',N) \in {\mathbf {S}}^{na}(M')$
for all
![]() $i<\lambda ^+$
. If
$i<\lambda ^+$
. If
![]() $|\{{\mathbf {gtp}}(a_i/M', N) : i<\lambda ^+\}|=\lambda ^+$
, it follows from stability for
$|\{{\mathbf {gtp}}(a_i/M', N) : i<\lambda ^+\}|=\lambda ^+$
, it follows from stability for
![]() $\lambda $
-algebraic types in
$\lambda $
-algebraic types in
![]() $\lambda $
that for some
$\lambda $
that for some
![]() $i < \lambda ^+$
,
$i < \lambda ^+$
,
![]() ${\mathbf {gtp}}(a_i/M', N) \in {\mathbf {S}}^{\lambda -ext}(M)$
. Otherwise
${\mathbf {gtp}}(a_i/M', N) \in {\mathbf {S}}^{\lambda -ext}(M)$
. Otherwise
![]() $| \{{\mathbf {gtp}}(a_i/M', N) : i<\lambda ^+\}|\leq \lambda $
. Let
$| \{{\mathbf {gtp}}(a_i/M', N) : i<\lambda ^+\}|\leq \lambda $
. Let
![]() $\Phi : \lambda ^+ \to \{{\mathbf {gtp}}(a_i/M', N) : i<\lambda ^+\}$
be given by
$\Phi : \lambda ^+ \to \{{\mathbf {gtp}}(a_i/M', N) : i<\lambda ^+\}$
be given by
![]() $i\mapsto {\mathbf {gtp}}(a_i/M',N)$
. Since
$i\mapsto {\mathbf {gtp}}(a_i/M',N)$
. Since
![]() $|\{{\mathbf {gtp}}(a_i/M', N) : i<\lambda ^+\}|\leq \lambda $
, by the pigeonhole principle there is
$|\{{\mathbf {gtp}}(a_i/M', N) : i<\lambda ^+\}|\leq \lambda $
, by the pigeonhole principle there is
![]() $q\in \{{\mathbf {gtp}}(a_i/M', N) : i<\lambda ^+\}$
such that
$q\in \{{\mathbf {gtp}}(a_i/M', N) : i<\lambda ^+\}$
such that
![]() $|\{ i <\lambda ^+: \Phi (i)=q\}| \geq \lambda ^+$
. That is, q has
$|\{ i <\lambda ^+: \Phi (i)=q\}| \geq \lambda ^+$
. That is, q has
![]() $\lambda ^+$
-many realizations in N. Hence q has the
$\lambda ^+$
-many realizations in N. Hence q has the
![]() $\lambda $
-extension property by the equivalence between (1) and (2) for q.
$\lambda $
-extension property by the equivalence between (1) and (2) for q.
Assume
![]() ${\mathbf {K}}$
is stable in
${\mathbf {K}}$
is stable in
![]() $\lambda $
. (1) implies (4) is clear as universal extensions exists by stability in
$\lambda $
. (1) implies (4) is clear as universal extensions exists by stability in
![]() $\lambda $
, so we only need to show (4) implies (2).
$\lambda $
, so we only need to show (4) implies (2).
Assume that
![]() $p:={\mathbf {gtp}}(a/M,N)$
has an extension to
$p:={\mathbf {gtp}}(a/M,N)$
has an extension to
![]() $q = {\mathbf {gtp}}(b/M',N') \in {\mathbf {S}}^{na}(M')$
for a universal extension
$q = {\mathbf {gtp}}(b/M',N') \in {\mathbf {S}}^{na}(M')$
for a universal extension
![]() $M'$
of M. We build
$M'$
of M. We build
![]() $\langle M_i: i<\lambda ^+\rangle $
increasing continuous such that
$\langle M_i: i<\lambda ^+\rangle $
increasing continuous such that
![]() $M_0 = M$
and for all i, there is
$M_0 = M$
and for all i, there is
![]() $a_i\in |M_{i+1}|-|M_i|$
realizing
$a_i\in |M_{i+1}|-|M_i|$
realizing
![]() ${\mathbf {gtp}}(a/M,N)$
. If we can carry out this construction we are done as
${\mathbf {gtp}}(a/M,N)$
. If we can carry out this construction we are done as
![]() $\bigcup _{i < \lambda ^+} M_i$
has
$\bigcup _{i < \lambda ^+} M_i$
has
![]() $\lambda ^+$
realizations of
$\lambda ^+$
realizations of
![]() ${\mathbf {gtp}}(a/M,N)$
. The base step and limit steps are clear, so we only need to do the successor step. Since
${\mathbf {gtp}}(a/M,N)$
. The base step and limit steps are clear, so we only need to do the successor step. Since
![]() $M'$
is universal over M, there is
$M'$
is universal over M, there is
![]() $f:M_i \to M'$
with
$f:M_i \to M'$
with
![]() $f\upharpoonright _M = id_M$
. Let
$f\upharpoonright _M = id_M$
. Let
![]() $M_{i+1} \in {\mathbf {K}}_\lambda $
and
$M_{i+1} \in {\mathbf {K}}_\lambda $
and
![]() $g: M_{i+1} \cong N'$
such that
$g: M_{i+1} \cong N'$
such that
![]() $M_i \le _{{\mathbf {K}}} M_{i+1}$
and
$M_i \le _{{\mathbf {K}}} M_{i+1}$
and
![]() $g\upharpoonright _{M_i} = f\upharpoonright _{M_i}$
. Let
$g\upharpoonright _{M_i} = f\upharpoonright _{M_i}$
. Let
![]() $a_{i+1} = g^{-1}(b)$
. It is straightforward to show that
$a_{i+1} = g^{-1}(b)$
. It is straightforward to show that
![]() $a_{i+1}$
is as required.
$a_{i+1}$
is as required.
We show that there are types with the
![]() $\lambda $
-extension property.
$\lambda $
-extension property.
Lemma 3.7. Assume that
![]() ${\mathbf {K}}$
has amalgamation in
${\mathbf {K}}$
has amalgamation in
![]() $\lambda $
and no maximal model in
$\lambda $
and no maximal model in
![]() $\lambda $
. If
$\lambda $
. If
![]() ${\mathbf {K}}$
is stable for
${\mathbf {K}}$
is stable for
![]() $\lambda $
-algebraic types in
$\lambda $
-algebraic types in
![]() $\lambda $
, then there is
$\lambda $
, then there is
![]() $p\in {\mathbf {S}}^{\lambda -ext}(M)$
for every
$p\in {\mathbf {S}}^{\lambda -ext}(M)$
for every
![]() $M \in {\mathbf {K}}_\lambda $
.
$M \in {\mathbf {K}}_\lambda $
.
Proof Fix
![]() $M\in {\mathbf {K}}_\lambda $
. There are two cases to consider. If
$M\in {\mathbf {K}}_\lambda $
. There are two cases to consider. If
![]() $|{\mathbf {S}}^{na}(M)|\geq \lambda ^+$
, the result follows directly from the assumption that
$|{\mathbf {S}}^{na}(M)|\geq \lambda ^+$
, the result follows directly from the assumption that
![]() ${\mathbf {K}}$
is stable for
${\mathbf {K}}$
is stable for
![]() $\lambda $
-algebraic types in
$\lambda $
-algebraic types in
![]() $\lambda $
. If
$\lambda $
. If
![]() $|{\mathbf {S}}^{na}(M)|\leq \lambda $
, then a similar argument to that of (2) implies (3) of the previous lemma can be used to obtain the result.
$|{\mathbf {S}}^{na}(M)|\leq \lambda $
, then a similar argument to that of (2) implies (3) of the previous lemma can be used to obtain the result.
Recall the following notion. This notion was first introduced by Shelah in [Reference Shelah19, Lemma 6.1], called minimal types there. Note that this is a different notion from the minimal types of [Reference Shelah25]. These types are also called quasiminimal types in the literature (see, for example, [Reference Lessmann12]).
Definition 3.8.
![]() $p={\mathbf {gtp}}(a/M,N)$
is a
$p={\mathbf {gtp}}(a/M,N)$
is a
![]() $\lambda $
-unique type if:
$\lambda $
-unique type if:
-
(1)
 $p={\mathbf {gtp}}(a/M,N)$
has the
$p={\mathbf {gtp}}(a/M,N)$
has the
 $\lambda $
-extension property.
$\lambda $
-extension property. -
(2) For every
 $M'\in {\mathbf {K}}_\lambda \le _{{\mathbf {K}}} $
-extending M, p has at most one extension
$M'\in {\mathbf {K}}_\lambda \le _{{\mathbf {K}}} $
-extending M, p has at most one extension
 $q\in {\mathbf {S}}^{\lambda -ext}(M')$
.
$q\in {\mathbf {S}}^{\lambda -ext}(M')$
.
In this case we say that
![]() $p \in {\mathbf {S}}^{\lambda -unq}(M)$
.
$p \in {\mathbf {S}}^{\lambda -unq}(M)$
.
We show the existence of
![]() $\lambda $
-unique types. The argument is standard (see, for example, [Reference Baldwin and Lessmann6, Proposition 2.5]), but we provide the details to show that the argument can be carried out in this setting.
$\lambda $
-unique types. The argument is standard (see, for example, [Reference Baldwin and Lessmann6, Proposition 2.5]), but we provide the details to show that the argument can be carried out in this setting.
Lemma 3.9. Assume that
![]() ${\mathbf {K}}$
has amalgamation in
${\mathbf {K}}$
has amalgamation in
![]() $\lambda $
, no maximal model in
$\lambda $
, no maximal model in
![]() $\lambda $
, and is stable for
$\lambda $
, and is stable for
![]() $\lambda $
-algebraic types in
$\lambda $
-algebraic types in
![]() $\lambda $
. If
$\lambda $
. If
![]() $|{\mathbf {S}}^{na}(M)|<2^{\aleph _0}$
for every
$|{\mathbf {S}}^{na}(M)|<2^{\aleph _0}$
for every
![]() $M \in {\mathbf {K}}_\lambda $
, then for every
$M \in {\mathbf {K}}_\lambda $
, then for every
![]() $M_0\in {\mathbf {K}}_\lambda $
and
$M_0\in {\mathbf {K}}_\lambda $
and
![]() $p\in {\mathbf {S}}^{\lambda -ext}(M_0)$
, there is
$p\in {\mathbf {S}}^{\lambda -ext}(M_0)$
, there is
![]() $M_1\in {\mathbf {K}}_\lambda $
and
$M_1\in {\mathbf {K}}_\lambda $
and
![]() $q \in {\mathbf {S}}^{\lambda -unq}(M_1)$
such that
$q \in {\mathbf {S}}^{\lambda -unq}(M_1)$
such that
![]() $M_0 \le _{{\mathbf {K}}} M_1$
and q extends p.
$M_0 \le _{{\mathbf {K}}} M_1$
and q extends p.
Proof Assume that
![]() $|{\mathbf {S}}^{na}(M)|<2^{\aleph _0}$
for every
$|{\mathbf {S}}^{na}(M)|<2^{\aleph _0}$
for every
![]() $M \in {\mathbf {K}}_\lambda $
and assume for the sake of contradiction that the conclusion fails. Then there is
$M \in {\mathbf {K}}_\lambda $
and assume for the sake of contradiction that the conclusion fails. Then there is
![]() $M_0\in {\mathbf {K}}_\lambda $
and
$M_0\in {\mathbf {K}}_\lambda $
and
![]() $p\in {\mathbf {S}}^{\lambda -ext}(M_0)$
without a
$p\in {\mathbf {S}}^{\lambda -ext}(M_0)$
without a
![]() $\lambda $
-unique type above it.
$\lambda $
-unique type above it.
We build
![]() $\langle M_n : n <\omega \rangle $
and
$\langle M_n : n <\omega \rangle $
and
![]() $\langle p_\eta : \eta \in 2^{<\omega } \rangle $
by induction such that:
$\langle p_\eta : \eta \in 2^{<\omega } \rangle $
by induction such that:
-
(1)
 $p_{\langle \rangle }=p$
;
$p_{\langle \rangle }=p$
; -
(2) for every
 $\eta \in 2^{<\omega }$
,
$\eta \in 2^{<\omega }$
,
 $p_\eta \in {\mathbf {S}}^{\lambda -ext}(M_{\ell (\eta )})$
;
$p_\eta \in {\mathbf {S}}^{\lambda -ext}(M_{\ell (\eta )})$
; -
(3) for every
 $\eta \in 2^{<\omega }$
,
$\eta \in 2^{<\omega }$
,  .
.
![]() The base step is given, so we do the induction step. By induction hypothesis we have
The base step is given, so we do the induction step. By induction hypothesis we have
![]() $\langle p_\eta \in {\mathbf {S}}^{\lambda -ext}(M_n) : \eta \in 2^n \rangle $
. Since there is no
$\langle p_\eta \in {\mathbf {S}}^{\lambda -ext}(M_n) : \eta \in 2^n \rangle $
. Since there is no
![]() $\lambda $
-unique type above
$\lambda $
-unique type above
![]() $p_{\langle \rangle }$
and by Lemma 3.6, for every
$p_{\langle \rangle }$
and by Lemma 3.6, for every
![]() $\eta \in 2^n $
there are
$\eta \in 2^n $
there are
![]() $N_\eta \in {\mathbf {K}}_\lambda $
and
$N_\eta \in {\mathbf {K}}_\lambda $
and
![]() $q_\eta ^0$
,
$q_\eta ^0$
,
![]() $q_\eta ^1 \in {\mathbf {S}}^{\lambda -ext}(N_\eta )$
such that
$q_\eta ^1 \in {\mathbf {S}}^{\lambda -ext}(N_\eta )$
such that
![]() $q_\eta ^0$
,
$q_\eta ^0$
,
![]() $q_\eta ^1 \geq p_\eta $
and
$q_\eta ^1 \geq p_\eta $
and
![]() $q_\eta ^0 \neq q_\eta ^1$
.
$q_\eta ^0 \neq q_\eta ^1$
.
Using amalgamation in
![]() $\lambda $
we build
$\lambda $
we build
![]() $M_{n+1} \in {\mathbf {K}}_\lambda $
and
$M_{n+1} \in {\mathbf {K}}_\lambda $
and
![]() $\langle f_\eta : N_\eta \xrightarrow [M_n]{} M_{n+1} : \eta \in 2^n \rangle $
. Now for every
$\langle f_\eta : N_\eta \xrightarrow [M_n]{} M_{n+1} : \eta \in 2^n \rangle $
. Now for every
![]() $\eta \in 2^n$
, let
$\eta \in 2^n$
, let ![]() such that
such that ![]() and
and ![]() . These exist by Lemma 3.6. It is easy to show that
. These exist by Lemma 3.6. It is easy to show that
![]() $M_{n+1}$
and
$M_{n+1}$
and ![]() are as required.
are as required.
![]() Let
Let
![]() $N:=\bigcup _{n <\omega } M_n\in {\mathbf {K}}_\lambda $
. For every
$N:=\bigcup _{n <\omega } M_n\in {\mathbf {K}}_\lambda $
. For every
![]() $\eta \in 2^\omega $
, let
$\eta \in 2^\omega $
, let
![]() $p_\eta \in {\mathbf {S}}^{na}(N)$
be an upper bound of
$p_\eta \in {\mathbf {S}}^{na}(N)$
be an upper bound of
![]() $\langle p_{\eta \restriction _n} : n<\omega \rangle $
given by Fact 2.8. Observe that if
$\langle p_{\eta \restriction _n} : n<\omega \rangle $
given by Fact 2.8. Observe that if
![]() $\eta \neq \nu \in 2^\omega $
,
$\eta \neq \nu \in 2^\omega $
,
![]() $p_\eta \neq p_\nu $
. Then
$p_\eta \neq p_\nu $
. Then
![]() $|{\mathbf {S}}^{na}(N)| \geq 2^{\aleph _0}$
which contradicts our assumption.
$|{\mathbf {S}}^{na}(N)| \geq 2^{\aleph _0}$
which contradicts our assumption.
Remark 3.10. If
![]() $M\le _{{\mathbf {K}}} N$
,
$M\le _{{\mathbf {K}}} N$
,
![]() $p\in {\mathbf {S}}^{\lambda -unq}(M)$
,
$p\in {\mathbf {S}}^{\lambda -unq}(M)$
,
![]() $q \in {\mathbf {S}}^{\lambda -ext}(N)$
, and
$q \in {\mathbf {S}}^{\lambda -ext}(N)$
, and
![]() $q\geq p$
, then
$q\geq p$
, then
![]() $q\in {\mathbf {S}}^{\lambda -unq}(N)$
.
$q\in {\mathbf {S}}^{\lambda -unq}(N)$
.
We are ready to prove one of the main results of the paper.
Theorem 3.11. Assume that
![]() ${\mathbf {K}}$
has amalgamation in
${\mathbf {K}}$
has amalgamation in
![]() $\lambda $
, no maximal model in
$\lambda $
, no maximal model in
![]() $\lambda $
, and is stable for
$\lambda $
, and is stable for
![]() $\lambda $
-algebraic types in
$\lambda $
-algebraic types in
![]() $\lambda $
. If
$\lambda $
. If
![]() $|{\mathbf {S}}^{na}(M)|<2^{\aleph _0}$
for every
$|{\mathbf {S}}^{na}(M)|<2^{\aleph _0}$
for every
![]() $M \in {\mathbf {K}}_\lambda $
and
$M \in {\mathbf {K}}_\lambda $
and
![]() ${\mathbf {K}}$
is
${\mathbf {K}}$
is
![]() $(<\lambda ^+, \lambda )$
-local, then
$(<\lambda ^+, \lambda )$
-local, then
![]() ${\mathbf {K}}$
has a model of cardinality
${\mathbf {K}}$
has a model of cardinality
![]() $\lambda ^{++}$
.
$\lambda ^{++}$
.
Proof It is enough to show that
![]() ${\mathbf {K}}$
has no maximal models in
${\mathbf {K}}$
has no maximal models in
![]() $\lambda ^+$
.
$\lambda ^+$
.
Assume for the sake of contradiction that
![]() $M\in {\mathbf {K}}_{\lambda ^+}$
is a maximal model. Let
$M\in {\mathbf {K}}_{\lambda ^+}$
is a maximal model. Let
![]() $N\le _{{\mathbf {K}}} M$
such that
$N\le _{{\mathbf {K}}} M$
such that
![]() $N \in {\mathbf {K}}_\lambda $
. By the maximality of M together with Lemma 3.7, Lemma 3.9, and amalgamation in
$N \in {\mathbf {K}}_\lambda $
. By the maximality of M together with Lemma 3.7, Lemma 3.9, and amalgamation in
![]() $\lambda $
, there is
$\lambda $
, there is
![]() $M_0 \in {\mathbf {K}}_\lambda $
with
$M_0 \in {\mathbf {K}}_\lambda $
with
![]() $N \le _{{\mathbf {K}}} M_0 \le _{{\mathbf {K}}} M$
and
$N \le _{{\mathbf {K}}} M_0 \le _{{\mathbf {K}}} M$
and
![]() $q_0\in {\mathbf {S}}^{\lambda -unq}(M_0)$
. Let
$q_0\in {\mathbf {S}}^{\lambda -unq}(M_0)$
. Let
![]() $\langle M_i\in {\mathbf {K}}_\lambda : i<\lambda ^+\rangle $
be a resolution of M with
$\langle M_i\in {\mathbf {K}}_\lambda : i<\lambda ^+\rangle $
be a resolution of M with
![]() $M_0$
as before. We build
$M_0$
as before. We build
![]() $\langle p_i : i <\lambda ^+\rangle $
such that:
$\langle p_i : i <\lambda ^+\rangle $
such that:
-
(1)
 $p_0=q_0$
;
$p_0=q_0$
; -
(2) if
 $i< j< \lambda ^+$
, then
$i< j< \lambda ^+$
, then
 $p_i\leq p_j$
;
$p_i\leq p_j$
; -
(3) for every
 $i < \lambda ^+$
,
$i < \lambda ^+$
,
 $p_i\in {\mathbf {S}}^{\lambda -unq}(M_i)$
;
$p_i\in {\mathbf {S}}^{\lambda -unq}(M_i)$
; -
(4) for every
 $j < \lambda ^+$
,
$j < \lambda ^+$
,
 $\langle p_i : i<j\rangle $
is coherent .
$\langle p_i : i<j\rangle $
is coherent .
![]() The base step is given and the successor step can be achieved using Lemma 3.6 and Remark 3.10. So assume i is limit, and take
The base step is given and the successor step can be achieved using Lemma 3.6 and Remark 3.10. So assume i is limit, and take
![]() $p_i$
to be an upper bound of
$p_i$
to be an upper bound of
![]() $\langle p_j : j<i\rangle $
given by Fact 2.8. By Fact 2.8
$\langle p_j : j<i\rangle $
given by Fact 2.8. By Fact 2.8
![]() $\langle p_j : j<i +1 \rangle $
is coherent, so we only need to show that
$\langle p_j : j<i +1 \rangle $
is coherent, so we only need to show that
![]() $p_i \in {\mathbf {S}}^{\lambda -unq}(\bigcup _{j<i}M_j )$
.
$p_i \in {\mathbf {S}}^{\lambda -unq}(\bigcup _{j<i}M_j )$
.
By Remark 3.10 it suffices to show that
![]() $p_i \in {\mathbf {S}}^{\lambda -ext}(\bigcup _{j<i}M_j)$
. Since
$p_i \in {\mathbf {S}}^{\lambda -ext}(\bigcup _{j<i}M_j)$
. Since
![]() $p_0\in {\mathbf {S}}^{\lambda -unq}(M_0)$
and
$p_0\in {\mathbf {S}}^{\lambda -unq}(M_0)$
and
![]() $M_0\le _{{\mathbf {K}}} \bigcup _{j<i}M_j$
, there is
$M_0\le _{{\mathbf {K}}} \bigcup _{j<i}M_j$
, there is
![]() $q\in {\mathbf {S}}^{\lambda -ext}(\bigcup _{j < i} M_j)$
such that
$q\in {\mathbf {S}}^{\lambda -ext}(\bigcup _{j < i} M_j)$
such that
![]() $q\geq p_0$
by Lemma 3.6.
$q\geq p_0$
by Lemma 3.6.
We show that for every
![]() $j<i$
,
$j<i$
,
![]() $q\restriction _{M_j}=p_i\restriction _{M_j}$
. Let
$q\restriction _{M_j}=p_i\restriction _{M_j}$
. Let
![]() $j<i$
. Since
$j<i$
. Since
![]() $q\restriction _{M_j}\in {\mathbf {S}}^{\lambda -ext}(M_j)$
,
$q\restriction _{M_j}\in {\mathbf {S}}^{\lambda -ext}(M_j)$
,
![]() $p_i\restriction _{M_j}=p_j \in {\mathbf {S}}^{\lambda -ext}(M_j)$
and both extend
$p_i\restriction _{M_j}=p_j \in {\mathbf {S}}^{\lambda -ext}(M_j)$
and both extend
![]() $p_0$
a
$p_0$
a
![]() $\lambda $
-unique type,
$\lambda $
-unique type,
![]() $q\restriction _{M_j}=p_i\restriction _{M_j}$
.
$q\restriction _{M_j}=p_i\restriction _{M_j}$
.
Therefore,
![]() $q = p_i$
as
$q = p_i$
as
![]() ${\mathbf {K}}$
is
${\mathbf {K}}$
is
![]() $(<\lambda ^+, \lambda )$
-local. Hence
$(<\lambda ^+, \lambda )$
-local. Hence
![]() $p_i \in {\mathbf {S}}^{\lambda -ext}(\bigcup _{j<i}M_j)$
as
$p_i \in {\mathbf {S}}^{\lambda -ext}(\bigcup _{j<i}M_j)$
as
![]() $q\in {\mathbf {S}}^{\lambda -ext}(\bigcup _{j < i} M_j)$
.
$q\in {\mathbf {S}}^{\lambda -ext}(\bigcup _{j < i} M_j)$
.
![]() Let
Let
![]() $q^*\in {\mathbf {S}}^{na}(M)$
be an upper bound of the coherent sequence
$q^*\in {\mathbf {S}}^{na}(M)$
be an upper bound of the coherent sequence
![]() $\langle p_i : i <\lambda ^+\rangle $
given by Fact 2.8. As
$\langle p_i : i <\lambda ^+\rangle $
given by Fact 2.8. As
![]() $q^*$
is a non-algebraic type, M has a proper extension which contradicts our assumption that M is maximal.
$q^*$
is a non-algebraic type, M has a proper extension which contradicts our assumption that M is maximal.
At the cost of strengthening the cardinal arithmetic hypothesis from
![]() $\lambda <2^{\aleph _0}$
to
$\lambda <2^{\aleph _0}$
to
![]() $\lambda ^+ <2^{\aleph _0}$
we can drop the assumption that
$\lambda ^+ <2^{\aleph _0}$
we can drop the assumption that
![]() $|{\mathbf {S}}^{na}(M)|<2^{\aleph _0}$
for every
$|{\mathbf {S}}^{na}(M)|<2^{\aleph _0}$
for every
![]() $M \in {\mathbf {K}}_\lambda $
.
$M \in {\mathbf {K}}_\lambda $
.
Lemma 3.12. Suppose
![]() $\lambda ^+<2^{\aleph _0}$
. Assume
$\lambda ^+<2^{\aleph _0}$
. Assume
![]() ${\mathbf {K}}$
has amalgamation in
${\mathbf {K}}$
has amalgamation in
![]() $\lambda $
, no maximal model in
$\lambda $
, no maximal model in
![]() $\lambda $
, and is stable for
$\lambda $
, and is stable for
![]() $\lambda $
-algebraic types in
$\lambda $
-algebraic types in
![]() $\lambda $
. If
$\lambda $
. If
![]() ${\mathbf {K}}$
is
${\mathbf {K}}$
is
![]() $(<\lambda ^+, \lambda )$
-local, then
$(<\lambda ^+, \lambda )$
-local, then
![]() ${\mathbf {K}}$
has a model of cardinality
${\mathbf {K}}$
has a model of cardinality
![]() $\lambda ^{++}$
.
$\lambda ^{++}$
.
Proof Assume for the sake of contradiction that
![]() ${\mathbf {K}}_{\lambda ^{++}}=\emptyset $
. We show that for every
${\mathbf {K}}_{\lambda ^{++}}=\emptyset $
. We show that for every
![]() $M\in {\mathbf {K}}_\lambda $
,
$M\in {\mathbf {K}}_\lambda $
,
![]() $|{\mathbf {S}}^{na}(M)| < 2^{\aleph _0}$
. This is enough by Theorem 3.11.
$|{\mathbf {S}}^{na}(M)| < 2^{\aleph _0}$
. This is enough by Theorem 3.11.
Let
![]() $M\in {\mathbf {K}}_\lambda $
. Then there is
$M\in {\mathbf {K}}_\lambda $
. Then there is
![]() $M \le _{\mathbf {K}} N\in {\mathbf {K}}_{\lambda ^+}$
maximal. Every
$M \le _{\mathbf {K}} N\in {\mathbf {K}}_{\lambda ^+}$
maximal. Every
![]() $p\in {\mathbf {S}}^{na}(M)$
is realized in N by amalgamation in
$p\in {\mathbf {S}}^{na}(M)$
is realized in N by amalgamation in
![]() $\lambda $
and maximality of N. Thus
$\lambda $
and maximality of N. Thus
![]() $|{\mathbf {S}}^{na}(M)|\leq \| N \| = \lambda ^+$
. Since
$|{\mathbf {S}}^{na}(M)|\leq \| N \| = \lambda ^+$
. Since
![]() $\lambda ^+<2^{\aleph _0}$
by assumption,
$\lambda ^+<2^{\aleph _0}$
by assumption,
![]() $|{\mathbf {S}}^{na}(M)| < 2^{\aleph _0}$
.
$|{\mathbf {S}}^{na}(M)| < 2^{\aleph _0}$
.
Remark 3.13. Theorem 3.11 and Lemma 3.12 are new even for universal classes with countable Löwenheim–Skolem–Tarski number and
![]() $\lambda = \aleph _0$
.
$\lambda = \aleph _0$
.
We use Theorem 3.11 to obtain the result mentioned in the abstract.
Theorem 3.14. Suppose
![]() $\lambda <2^{\aleph _0}$
. Let
$\lambda <2^{\aleph _0}$
. Let
![]() ${\mathbf {K}}$
be an abstract elementary class with
${\mathbf {K}}$
be an abstract elementary class with
![]() $\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
. Assume
$\lambda \geq {\operatorname {LS}}({\mathbf {K}})$
. Assume
![]() ${\mathbf {K}}$
has amalgamation in
${\mathbf {K}}$
has amalgamation in
![]() $\lambda $
, no maximal model in
$\lambda $
, no maximal model in
![]() $\lambda $
, and is stable in
$\lambda $
, and is stable in
![]() $\lambda $
. If
$\lambda $
. If
![]() ${\mathbf {K}}$
is
${\mathbf {K}}$
is
![]() $(<\lambda ^+, \lambda )$
-local, then
$(<\lambda ^+, \lambda )$
-local, then
![]() ${\mathbf {K}}$
has a model of cardinality
${\mathbf {K}}$
has a model of cardinality
![]() $\lambda ^{++}$
.
$\lambda ^{++}$
.
Proof We show that for every
![]() $M\in {\mathbf {K}}_\lambda $
,
$M\in {\mathbf {K}}_\lambda $
,
![]() $|{\mathbf {S}}^{na}(M)| < 2^{\aleph _0}$
. This is enough by Theorem 3.11. Let
$|{\mathbf {S}}^{na}(M)| < 2^{\aleph _0}$
. This is enough by Theorem 3.11. Let
![]() $M\in {\mathbf {K}}_\lambda $
.
$M\in {\mathbf {K}}_\lambda $
.
![]() $|{\mathbf {S}}^{na}(M)|\leq \lambda $
by stability in
$|{\mathbf {S}}^{na}(M)|\leq \lambda $
by stability in
![]() $\lambda $
. Since
$\lambda $
. Since
![]() $\lambda <2^{\aleph _0}$
by assumption,
$\lambda <2^{\aleph _0}$
by assumption,
![]() $|{\mathbf {S}}^{na}(M)| < 2^{\aleph _0}$
.
$|{\mathbf {S}}^{na}(M)| < 2^{\aleph _0}$
.
Remark 3.15. For AECs
![]() ${\mathbf {K}}$
with
${\mathbf {K}}$
with
![]() ${\operatorname {LS}}({\mathbf {K}})> \aleph _0$
or
${\operatorname {LS}}({\mathbf {K}})> \aleph _0$
or
![]() $\lambda> \aleph _0$
, the result is new even for universal classes. For AECs
$\lambda> \aleph _0$
, the result is new even for universal classes. For AECs
![]() ${\mathbf {K}}$
with
${\mathbf {K}}$
with
![]() ${\operatorname {LS}}({\mathbf {K}})= \aleph _0$
and
${\operatorname {LS}}({\mathbf {K}})= \aleph _0$
and
![]() $\lambda = \aleph _0$
, the assumption that
$\lambda = \aleph _0$
, the assumption that
![]() $\lambda < 2^{\aleph _0}$
is vacuous. This result for
$\lambda < 2^{\aleph _0}$
is vacuous. This result for
![]() $(<\aleph _0, \aleph _0)$
-tame AECs can be obtained using [Reference Shelah and Vasey27, Corollay 4.7], [Reference Shelah and Vasey27, Theorem 5.8], and [Reference Shelah26, Chapter II.4.13], but the result has never been stated in the literature. Moreover, the argument presented in this paper is significantly simpler than the argument using the results of Shelah and Vasey. Furthermore, the result is new for
$(<\aleph _0, \aleph _0)$
-tame AECs can be obtained using [Reference Shelah and Vasey27, Corollay 4.7], [Reference Shelah and Vasey27, Theorem 5.8], and [Reference Shelah26, Chapter II.4.13], but the result has never been stated in the literature. Moreover, the argument presented in this paper is significantly simpler than the argument using the results of Shelah and Vasey. Furthermore, the result is new for
![]() $(\aleph _0, \aleph _0)$
-local AECs.
$(\aleph _0, \aleph _0)$
-local AECs.
Funding
The first author’s research was partially supported by an AMS-Simons Travel Grant 2022–2024.