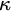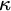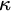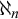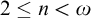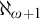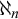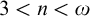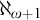1. Introduction
Obtaining compactness properties at many successive cardinals simultaneously is a long-running project of set theory. The tree property and its generalizations have been of particular interest. The starting point for this program was a result of Mitchell and Silver [Reference Mitchell12], who showed that it is consistent from a weakly compact cardinal for the tree property to hold at
![]() $\aleph _2$
; their techniques have formed the blueprint for obtaining the tree property at successors of regular cardinals. Abraham [Reference Abraham1] showed that it is possible for the tree property to hold at
$\aleph _2$
; their techniques have formed the blueprint for obtaining the tree property at successors of regular cardinals. Abraham [Reference Abraham1] showed that it is possible for the tree property to hold at
![]() $\aleph _2$
and
$\aleph _2$
and
![]() $\aleph _3$
simultaneously, starting from a supercompact cardinal and a weakly compact cardinal. Cummings and Foreman [Reference Cummings and Foreman2], starting with
$\aleph _3$
simultaneously, starting from a supercompact cardinal and a weakly compact cardinal. Cummings and Foreman [Reference Cummings and Foreman2], starting with
![]() $\omega $
many supercompacts, produced a model in which the tree property holds at
$\omega $
many supercompacts, produced a model in which the tree property holds at
![]() $\aleph _n$
for
$\aleph _n$
for
![]() $2 \leq n < \omega $
.
$2 \leq n < \omega $
.
Different techniques are required to obtain the tree property at the successor of a singular cardinal. Magidor and Shelah [Reference Magidor and Shelah11] showed that the tree property could hold at
![]() $\aleph _{\omega +1}$
using very strong large cardinal assumptions; these assumptions were reduced to
$\aleph _{\omega +1}$
using very strong large cardinal assumptions; these assumptions were reduced to
![]() $\omega $
supercompacts by Sinapova [Reference Sinapova16]. Similar results can be obtained at the successors of singular cardinals of uncountable cofinality. Building off techniques of Neeman [Reference Neeman13], Sinapova [Reference Sinapova15] showed that the tree property could consistently hold at the successor of a singular cardinal of any cofinality (along with the failure of SCH). Golshani [Reference Golshani6] further refined this result, showing that the tree property could hold at
$\omega $
supercompacts by Sinapova [Reference Sinapova16]. Similar results can be obtained at the successors of singular cardinals of uncountable cofinality. Building off techniques of Neeman [Reference Neeman13], Sinapova [Reference Sinapova15] showed that the tree property could consistently hold at the successor of a singular cardinal of any cofinality (along with the failure of SCH). Golshani [Reference Golshani6] further refined this result, showing that the tree property could hold at
![]() $\aleph _{\gamma +1}$
for any limit ordinal
$\aleph _{\gamma +1}$
for any limit ordinal
![]() $\gamma $
. Neeman [Reference Neeman14] was able to combine the techniques for obtaining the tree property at successors of regular cardinals and successors of singular cardinals, producing a model in which the tree property holds at
$\gamma $
. Neeman [Reference Neeman14] was able to combine the techniques for obtaining the tree property at successors of regular cardinals and successors of singular cardinals, producing a model in which the tree property holds at
![]() $\aleph _n$
for
$\aleph _n$
for
![]() $2\leq n < \omega $
and at
$2\leq n < \omega $
and at
![]() $\aleph _{\omega +1}$
simultaneously.
$\aleph _{\omega +1}$
simultaneously.
We now turn our attention to generalizations of the tree property. Two generalizations of interest, due to Jech and Magidor respectively, are the strong tree property and the super tree property (also known as ITP). These properties characterize strong compactness and supercompactness up to inaccessibility in much the same way that the tree property characterizes weak compactness. In particular, if
![]() $\kappa $
is inaccessible, then:
$\kappa $
is inaccessible, then:
-
• The tree property holds at
 $\kappa $
if and only if
$\kappa $
if and only if
 $\kappa $
is weakly compact.
$\kappa $
is weakly compact. -
• (Jech [Reference Jech9]) The strong tree property holds at
 $\kappa $
if and only if
$\kappa $
if and only if
 $\kappa $
is strongly compact.
$\kappa $
is strongly compact. -
• (Magidor [Reference Magidor10]) The super tree property (ITP) holds at
 $\kappa $
if and only if
$\kappa $
if and only if
 $\kappa $
is supercompact.
$\kappa $
is supercompact.
Although these properties were originally examined in the 1970s, recent work of Weiß, who studied these properties in his thesis [Reference Weiß18], has sparked a number of new results. Fontanella [Reference Fontanella3] generalized Abraham’s result to obtain ITP at
![]() $\aleph _2$
and
$\aleph _2$
and
![]() $\aleph _3$
simultaneously. Shortly thereafter, Fontanella [Reference Fontanella4] and Unger [Reference Unger17] independently showed that in the model of Cummings and Foreman, ITP holds at each
$\aleph _3$
simultaneously. Shortly thereafter, Fontanella [Reference Fontanella4] and Unger [Reference Unger17] independently showed that in the model of Cummings and Foreman, ITP holds at each
![]() $\aleph _n$
. Fontanella [Reference Fontanella5] also showed that assuming
$\aleph _n$
. Fontanella [Reference Fontanella5] also showed that assuming
![]() $\omega $
-many supercompact cardinals, the strong tree property could consistently hold at
$\omega $
-many supercompact cardinals, the strong tree property could consistently hold at
![]() $\aleph _{\omega +1}$
. Hachtman and Sinapova [Reference Hachtman and Sinapova8] generalized this result further, showing that from the same assumptions it is consistent to have ITP at
$\aleph _{\omega +1}$
. Hachtman and Sinapova [Reference Hachtman and Sinapova8] generalized this result further, showing that from the same assumptions it is consistent to have ITP at
![]() $\aleph _{\omega +1}$
.
$\aleph _{\omega +1}$
.
In this paper, we continue the analysis of the strong and super tree properties at successors of singular cardinals and at small successor cardinals simultaneously. In Section 3, we show that in Neeman’s construction in [Reference Neeman14], ITP holds at each
![]() $\aleph _n$
, and the strong tree property holds at
$\aleph _n$
, and the strong tree property holds at
![]() $\aleph _{\omega +1}$
. This answers a question of Fontanella, who asked if it was consistent to have the strong tree property up to
$\aleph _{\omega +1}$
. This answers a question of Fontanella, who asked if it was consistent to have the strong tree property up to
![]() $\aleph _{\omega +1}$
. The key step in this argument is Theorem 3.14, which describes a general class of forcings in which the strong tree property holds at the successor of a singular. This theorem applies to singular cardinals of any cofinality.
$\aleph _{\omega +1}$
. The key step in this argument is Theorem 3.14, which describes a general class of forcings in which the strong tree property holds at the successor of a singular. This theorem applies to singular cardinals of any cofinality.
Next, we consider ITP at successors of singular cardinals. In Section 4, we describe a similar class of forcings in which ITP holds at the successor of a singular. Once again, there are no restrictions on the cofinality of this singular cardinal. We use this to show that from
![]() $\tau $
-many supercompacts it is consistent to have ITP at
$\tau $
-many supercompacts it is consistent to have ITP at
![]() $\aleph _{\tau +1}$
for any regular
$\aleph _{\tau +1}$
for any regular
![]() $\tau $
with
$\tau $
with
![]() $\tau < \aleph _\tau $
. In Section 5, we apply this technique to show that in a modified version of Neeman’s model, ITP holds at
$\tau < \aleph _\tau $
. In Section 5, we apply this technique to show that in a modified version of Neeman’s model, ITP holds at
![]() $\aleph _{\omega +1}$
and at
$\aleph _{\omega +1}$
and at
![]() $\aleph _n$
for all
$\aleph _n$
for all
![]() $n> 3$
. This is a partial answer to a question of Hachtman and Sinapova, who asked if ITP could be obtained up to
$n> 3$
. This is a partial answer to a question of Hachtman and Sinapova, who asked if ITP could be obtained up to
![]() $\aleph _{\omega +1}$
.
$\aleph _{\omega +1}$
.
Finally, in Section 6, we show that these techniques can also be applied to obtain the strong and/or super tree properties at successors of small singular cardinals of multiple cofinalities simultaneously. In particular, given a finite increasing sequence
![]() $\alpha _0, \dots , \alpha _n$
of ordinals where for each
$\alpha _0, \dots , \alpha _n$
of ordinals where for each
![]() $i \leq n, \alpha _i < \omega _{\alpha _i}$
and
$i \leq n, \alpha _i < \omega _{\alpha _i}$
and
![]() $\omega _{\alpha _i}$
is a regular cardinal, we describe a model in which we obtain these properties at
$\omega _{\alpha _i}$
is a regular cardinal, we describe a model in which we obtain these properties at
![]() $\aleph _{\omega _{\alpha _i}+1}$
for all
$\aleph _{\omega _{\alpha _i}+1}$
for all
![]() $i \leq n$
. If
$i \leq n$
. If
![]() $\alpha _{i+1}> \alpha _i+1$
, we obtain ITP at
$\alpha _{i+1}> \alpha _i+1$
, we obtain ITP at
![]() $\aleph _{\omega _{\alpha _i}+1}$
; otherwise, we can obtain the strong tree property. Our large cardinal hypotheses here are somewhat stronger than in other sections; we require
$\aleph _{\omega _{\alpha _i}+1}$
; otherwise, we can obtain the strong tree property. Our large cardinal hypotheses here are somewhat stronger than in other sections; we require
![]() $\kappa _0$
-many supercompacts, where
$\kappa _0$
-many supercompacts, where
![]() $\kappa _0$
is itself supercompact.
$\kappa _0$
is itself supercompact.
On notation: we use the convention that a poset is
![]() $\kappa $
-closed if every descending sequence of size less than
$\kappa $
-closed if every descending sequence of size less than
![]() $\kappa $
has a lower bound. If
$\kappa $
has a lower bound. If
![]() $\mathbb {P}$
is a forcing notion over a model V, we will use
$\mathbb {P}$
is a forcing notion over a model V, we will use
![]() $V[\mathbb {P}]$
to denote the extension of V by some generic for
$V[\mathbb {P}]$
to denote the extension of V by some generic for
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
2. Preliminaries and branch lemmas
We begin by defining the strong tree property and ITP.
Definition 2.1. Let
![]() $\mu $
be a regular cardinal and let
$\mu $
be a regular cardinal and let
![]() $\lambda \geq \mu $
. A set
$\lambda \geq \mu $
. A set
![]() $d = \langle d_z \mid z\in \mathcal {P}_\mu (\lambda )\rangle $
is a
$d = \langle d_z \mid z\in \mathcal {P}_\mu (\lambda )\rangle $
is a
![]() $\mathcal {P}_\mu (\lambda )$
-list if for all
$\mathcal {P}_\mu (\lambda )$
-list if for all
![]() $z \in \mathcal {P}_\mu (\lambda )$
,
$z \in \mathcal {P}_\mu (\lambda )$
,
![]() $d_z\subseteq z$
. We define the zth level of a list, denoted
$d_z\subseteq z$
. We define the zth level of a list, denoted
![]() $L_z$
, by
$L_z$
, by
A
![]() $\mathcal {P}_\mu (\lambda )$
-list is thin if
$\mathcal {P}_\mu (\lambda )$
-list is thin if
![]() $|L_z| < \mu $
for all
$|L_z| < \mu $
for all
![]() $z \in \mathcal {P}_\mu (\lambda )$
.
$z \in \mathcal {P}_\mu (\lambda )$
.
Note that if
![]() $\mu $
is inaccessible, every
$\mu $
is inaccessible, every
![]() $\mathcal {P}_\mu (\lambda )$
list is thin.
$\mathcal {P}_\mu (\lambda )$
list is thin.
Definition 2.2. A set
![]() $b \subseteq \lambda $
is a cofinal branch through a
$b \subseteq \lambda $
is a cofinal branch through a
![]() $\mathcal {P}_\mu (\lambda )$
-list d if for all
$\mathcal {P}_\mu (\lambda )$
-list d if for all
![]() $x \in \mathcal {P}_\mu (\lambda )$
there is
$x \in \mathcal {P}_\mu (\lambda )$
there is
![]() $z \supseteq x$
such that
$z \supseteq x$
such that
![]() $b\cap x = d_z\cap x$
. In other words, for all x,
$b\cap x = d_z\cap x$
. In other words, for all x,
![]() $b \cap x \in L_x$
. We say that the strong tree property holds at
$b \cap x \in L_x$
. We say that the strong tree property holds at
![]() $\mu $
if for all
$\mu $
if for all
![]() $\lambda \geq \mu $
, every thin
$\lambda \geq \mu $
, every thin
![]() $\mathcal {P}_\mu (\lambda )$
-list has a cofinal branch.
$\mathcal {P}_\mu (\lambda )$
-list has a cofinal branch.
Definition 2.3. A set
![]() $b \subseteq \lambda $
is an ineffable branch through a
$b \subseteq \lambda $
is an ineffable branch through a
![]() $\mathcal {P}_\mu (\lambda )$
-list d if
$\mathcal {P}_\mu (\lambda )$
-list d if
![]() $\{z \in \mathcal {P}_\mu (\lambda ) \mid b \cap z = d_z\}$
is stationary. We say
$\{z \in \mathcal {P}_\mu (\lambda ) \mid b \cap z = d_z\}$
is stationary. We say
![]() $\operatorname {\mathrm {ITP}}(\mu ,\lambda )$
holds if every thin
$\operatorname {\mathrm {ITP}}(\mu ,\lambda )$
holds if every thin
![]() $\mathcal {P}_\mu (\lambda )$
-list has an ineffable branch. We say ITP holds at
$\mathcal {P}_\mu (\lambda )$
-list has an ineffable branch. We say ITP holds at
![]() $\mu $
if
$\mu $
if
![]() $\operatorname {\mathrm {ITP}}(\mu ,\lambda )$
holds for all
$\operatorname {\mathrm {ITP}}(\mu ,\lambda )$
holds for all
![]() $\lambda \geq \mu $
.
$\lambda \geq \mu $
.
Note that every ineffable branch is cofinal.
Fact 2.4 [Reference Weiß19, Proposition 3.4].
Let
![]() $\lambda '> \lambda $
.
$\lambda '> \lambda $
.
![]() $\operatorname {\mathrm {ITP}}(\mu , \lambda ')$
implies
$\operatorname {\mathrm {ITP}}(\mu , \lambda ')$
implies
![]() $\operatorname {\mathrm {ITP}}(\mu , \lambda )$
.
$\operatorname {\mathrm {ITP}}(\mu , \lambda )$
.
Fact 2.5 [Reference Fontanella5, Lemma 3.4].
Let
![]() $\lambda '> \lambda $
. If every thin
$\lambda '> \lambda $
. If every thin
![]() $\mathcal {P}_\mu (\lambda ')$
-list has a cofinal branch, then so does every thin
$\mathcal {P}_\mu (\lambda ')$
-list has a cofinal branch, then so does every thin
![]() $\mathcal {P}_\mu (\lambda )$
list.
$\mathcal {P}_\mu (\lambda )$
list.
ITP, like the tree property, is usually obtained at the successor of regular cardinals by means of a lifted embedding. This will produce a branch in the generic extension containing the embedding, as described in the following lemma.
Lemma 2.6. Let W be a model of set theory, and let d be a thin
![]() $\mathcal {P}_\kappa (\lambda )$
list. Suppose that in some extension
$\mathcal {P}_\kappa (\lambda )$
list. Suppose that in some extension
![]() $W[G]$
there is a generic embedding
$W[G]$
there is a generic embedding
![]() $j:W \to M$
with critical point
$j:W \to M$
with critical point
![]() $\kappa $
such that
$\kappa $
such that
![]() $j(\kappa )> \lambda $
and
$j(\kappa )> \lambda $
and
![]() $M^\lambda \subseteq M$
. Then in
$M^\lambda \subseteq M$
. Then in
![]() $W[G]$
, d has a cofinal branch b. Moreover, if
$W[G]$
, d has a cofinal branch b. Moreover, if
![]() $b \in W$
, then b is ineffable.
$b \in W$
, then b is ineffable.
Proof Work in
![]() $W[G]$
, and consider
$W[G]$
, and consider
![]() $j(d)$
. Since
$j(d)$
. Since
![]() $j(\kappa )> \lambda $
, we have that
$j(\kappa )> \lambda $
, we have that
![]() $j"\lambda \in \mathcal {P}_{j(\kappa )}(j(\lambda ))$
. Let
$j"\lambda \in \mathcal {P}_{j(\kappa )}(j(\lambda ))$
. Let
![]() $b = \{\alpha < \lambda \mid j(\alpha ) \in j(d)_{j"\lambda }\}$
.
$b = \{\alpha < \lambda \mid j(\alpha ) \in j(d)_{j"\lambda }\}$
.
We first claim that b is a cofinal branch. Let
![]() $z \in \mathcal {P}_\kappa (\lambda )^W$
. We want to show that
$z \in \mathcal {P}_\kappa (\lambda )^W$
. We want to show that
![]() $b \cap z \in L_z$
. Note that
$b \cap z \in L_z$
. Note that
![]() $j(d)_{j"\lambda }\cap j(z) \in j(L_z)$
. Since d is a thin list,
$j(d)_{j"\lambda }\cap j(z) \in j(L_z)$
. Since d is a thin list,
![]() $|L_z|< \kappa $
, so
$|L_z|< \kappa $
, so
![]() $j(L_z) = j"(L_z) = \{j(d)_{j(y)} \cap j(z) \mid z\subseteq y, y \in \mathcal {P}_\kappa (\lambda )^W\}$
. Since
$j(L_z) = j"(L_z) = \{j(d)_{j(y)} \cap j(z) \mid z\subseteq y, y \in \mathcal {P}_\kappa (\lambda )^W\}$
. Since
![]() $j(d)_{j"\lambda }\cap j(z) \in j(L_z)$
, there must be some y such that
$j(d)_{j"\lambda }\cap j(z) \in j(L_z)$
, there must be some y such that
![]() $j(d)_{j"\lambda }\cap j(z) = j(d)_{j(y)}\cap j(z)$
. It follows that
$j(d)_{j"\lambda }\cap j(z) = j(d)_{j(y)}\cap j(z)$
. It follows that
![]() $b\cap z = d_y\cap z$
.
$b\cap z = d_y\cap z$
.
Now, suppose that
![]() $b \in W$
. Let U be the normal measure on
$b \in W$
. Let U be the normal measure on
![]() $\mathcal {P}_\kappa (\lambda )^W$
corresponding to j. Note that in the ultrapower of W by U,
$\mathcal {P}_\kappa (\lambda )^W$
corresponding to j. Note that in the ultrapower of W by U,
![]() $j"\lambda $
is represented by
$j"\lambda $
is represented by
![]() $[x\to x]$
, and so
$[x\to x]$
, and so
![]() $j(d)_{j"\lambda }$
is represented by
$j(d)_{j"\lambda }$
is represented by
![]() $[x \mapsto d]_{[x\mapsto x]} = [x \mapsto d_x]$
. On the other hand, since
$[x \mapsto d]_{[x\mapsto x]} = [x \mapsto d_x]$
. On the other hand, since
![]() $b \in W$
, we can take
$b \in W$
, we can take
![]() $j(b)$
; indeed,
$j(b)$
; indeed,
![]() $j(d)_{j"\lambda } = j(b) \cap j"\lambda $
. Since
$j(d)_{j"\lambda } = j(b) \cap j"\lambda $
. Since
![]() $j(b)$
is represented by
$j(b)$
is represented by
![]() $[x \mapsto b]$
,
$[x \mapsto b]$
,
![]() $j(d)_{j"\lambda } = [x \mapsto b] \cap [x \mapsto x]$
. We conclude that
$j(d)_{j"\lambda } = [x \mapsto b] \cap [x \mapsto x]$
. We conclude that
![]() $d_x = b \cap x$
for U-many x. Since U is a normal measure on W, all measure one sets must be stationary in W, so b must be an ineffable branch.
$d_x = b \cap x$
for U-many x. Since U is a normal measure on W, all measure one sets must be stationary in W, so b must be an ineffable branch.
The next step is usually to show that the forcing could not have added a branch, so the branch must have already been present in W, and will thus be ineffable. The crucial ingredients in this process are branch preservation lemmas. To generalize the standard branch lemmas from trees to thin lists, we use the (thin) approximation property.
Definition 2.7. Let
![]() $\kappa $
be regular. A forcing
$\kappa $
be regular. A forcing
![]() $\mathbb {P}$
has the
$\mathbb {P}$
has the
![]() $\kappa $
-approximation property in a model V if for every ordinal
$\kappa $
-approximation property in a model V if for every ordinal
![]() $\lambda $
and every
$\lambda $
and every
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {b}$
for a subset of
$\dot {b}$
for a subset of
![]() $\lambda $
,
$\lambda $
,
![]() $\Vdash _{\mathbb {P}} \dot {b} \cap z \in V$
for all
$\Vdash _{\mathbb {P}} \dot {b} \cap z \in V$
for all
![]() $z \in (\mathcal {P}_\kappa (\lambda ))^V$
implies that
$z \in (\mathcal {P}_\kappa (\lambda ))^V$
implies that
![]() $\Vdash _{\mathbb {P}} \dot {b} \in V.$
$\Vdash _{\mathbb {P}} \dot {b} \in V.$
A poset
![]() $\mathbb {P}$
has the thin
$\mathbb {P}$
has the thin
![]() $\kappa $
-approximation property in V if for every ordinal
$\kappa $
-approximation property in V if for every ordinal
![]() $\lambda $
and every
$\lambda $
and every
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {b}$
for a subset of
$\dot {b}$
for a subset of
![]() $\lambda $
,
$\lambda $
,
![]() $\Vdash _{\mathbb {P}} \dot {b} \cap z \in V$
and
$\Vdash _{\mathbb {P}} \dot {b} \cap z \in V$
and
![]() $|\{x \in V \mid \exists p\in \mathbb {P} \ p \Vdash _{\mathbb {P}} x = \dot {b}\cap z\}|<\kappa $
for every
$|\{x \in V \mid \exists p\in \mathbb {P} \ p \Vdash _{\mathbb {P}} x = \dot {b}\cap z\}|<\kappa $
for every
![]() $z \in (\mathcal {P}_\kappa (\lambda ))^V$
implies that
$z \in (\mathcal {P}_\kappa (\lambda ))^V$
implies that
![]() $\Vdash _{\mathbb {P}} \dot {b} \in V$
.
$\Vdash _{\mathbb {P}} \dot {b} \in V$
.
Note that the thin
![]() $\kappa $
-approximation property is weaker than the
$\kappa $
-approximation property is weaker than the
![]() $\kappa $
-approximation property. We say that names meeting the hypotheses in Definition 2.7 are (thinly)
$\kappa $
-approximation property. We say that names meeting the hypotheses in Definition 2.7 are (thinly)
![]() $\kappa $
-approximated by
$\kappa $
-approximated by
![]() $\mathbb {P}$
over V. These properties are useful because a cofinal branch through a thin
$\mathbb {P}$
over V. These properties are useful because a cofinal branch through a thin
![]() $\mathcal {P}_\kappa (\lambda )$
list is always thinly approximated over V.
$\mathcal {P}_\kappa (\lambda )$
list is always thinly approximated over V.
Lemma 2.8. Let d be a thin
![]() $\mathcal {P}_\kappa (\lambda )$
list in V, and let
$\mathcal {P}_\kappa (\lambda )$
list in V, and let
![]() $\mathbb {P}$
be a notion of forcing over V. Suppose
$\mathbb {P}$
be a notion of forcing over V. Suppose
![]() $\dot {b}$
is a
$\dot {b}$
is a
![]() $\mathbb {P}$
-name for a cofinal branch through this list. Then
$\mathbb {P}$
-name for a cofinal branch through this list. Then
![]() $\dot {b}$
is thinly
$\dot {b}$
is thinly
![]() $\kappa $
-approximated by
$\kappa $
-approximated by
![]() $\mathbb {P}$
over V.
$\mathbb {P}$
over V.
Proof Let
![]() $\dot {b}$
be a name for a cofinal branch, and let
$\dot {b}$
be a name for a cofinal branch, and let
![]() $x \in (\mathcal {P}_\kappa (\lambda ))^V$
. Since
$x \in (\mathcal {P}_\kappa (\lambda ))^V$
. Since
![]() $\dot {b}$
is forced to be cofinal,
$\dot {b}$
is forced to be cofinal,
![]() $\dot {b}\cap x$
is forced to be in
$\dot {b}\cap x$
is forced to be in
![]() $L_x$
for all x. Since
$L_x$
for all x. Since
![]() $L_x$
is in V,
$L_x$
is in V,
![]() $\dot {b}\cap x$
is likewise forced to be in V. Since the list is thin,
$\dot {b}\cap x$
is likewise forced to be in V. Since the list is thin,
![]() $|L_x| < \kappa $
, and so there are fewer than
$|L_x| < \kappa $
, and so there are fewer than
![]() $\kappa $
possibilities for
$\kappa $
possibilities for
![]() $\dot {b}\cap x$
.
$\dot {b}\cap x$
.
Lemma 2.9 [Reference Unger17, Lemma 7.10].
Suppose that
![]() $\dot {b}$
is a
$\dot {b}$
is a
![]() $\mathbb {P}\ast \dot {\mathbb {Q}}$
-name for a subset of some ordinal
$\mathbb {P}\ast \dot {\mathbb {Q}}$
-name for a subset of some ordinal
![]() $\mu $
, which is
$\mu $
, which is
![]() $(thinly) \kappa $
-approximated by
$(thinly) \kappa $
-approximated by
![]() $\mathbb {P}\ast \dot {\mathbb {Q}}$
over V. If
$\mathbb {P}\ast \dot {\mathbb {Q}}$
over V. If
![]() $\mathbb {P}$
has the
$\mathbb {P}$
has the
![]() $\kappa $
-cc, then in
$\kappa $
-cc, then in
![]() $V[\mathbb {P}]$
,
$V[\mathbb {P}]$
,
![]() $\dot {b}$
is still
$\dot {b}$
is still
![]() $(thinly) \kappa $
-approximated by
$(thinly) \kappa $
-approximated by
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Proof Let G be generic for
![]() $\mathbb {P}$
over V. Since
$\mathbb {P}$
over V. Since
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\kappa $
-cc,
$\kappa $
-cc,
![]() $\mathcal {P}_\kappa (\mu )^V$
is cofinal in
$\mathcal {P}_\kappa (\mu )^V$
is cofinal in
![]() $\mathcal {P}_\kappa (\mu )^{V[G]}$
. In
$\mathcal {P}_\kappa (\mu )^{V[G]}$
. In
![]() $V[G]$
, if
$V[G]$
, if
![]() $x \in \mathcal {P}_\kappa (\mu )$
is a subset of some
$x \in \mathcal {P}_\kappa (\mu )$
is a subset of some
![]() $y \in \mathcal {P}_\kappa (\mu )^{V}$
, then
$y \in \mathcal {P}_\kappa (\mu )^{V}$
, then
![]() $\dot {b}\cap x$
is determined solely by
$\dot {b}\cap x$
is determined solely by
![]() $\dot {b}\cap y$
and x. Since
$\dot {b}\cap y$
and x. Since
![]() $\dot {b}$
is
$\dot {b}$
is
![]() $\kappa $
-approximated by
$\kappa $
-approximated by
![]() $\mathbb {P}\ast \dot {\mathbb {Q}}$
over V,
$\mathbb {P}\ast \dot {\mathbb {Q}}$
over V,
![]() $\dot {b}\cap y$
must be in V. It follows that
$\dot {b}\cap y$
must be in V. It follows that
![]() $\mathbb {Q}$
forces that
$\mathbb {Q}$
forces that
![]() $\dot {b}\cap x \in V[G]$
, as desired.
$\dot {b}\cap x \in V[G]$
, as desired.
Now suppose that
![]() $\dot {b}$
is thinly
$\dot {b}$
is thinly
![]() $\kappa $
-approximated by
$\kappa $
-approximated by
![]() $\mathbb {P}\ast \dot {\mathbb {Q}}$
, not just
$\mathbb {P}\ast \dot {\mathbb {Q}}$
, not just
![]() $\kappa $
-approximated. For every possible value of
$\kappa $
-approximated. For every possible value of
![]() $\dot {b}\cap x$
, we can always choose an extension that is a possible value for
$\dot {b}\cap x$
, we can always choose an extension that is a possible value for
![]() $\dot {b}\cap y$
. This defines an injection from the possible values (in
$\dot {b}\cap y$
. This defines an injection from the possible values (in
![]() $V[G]$
) of
$V[G]$
) of
![]() $\dot {b}\cap x$
to the possible values (in
$\dot {b}\cap x$
to the possible values (in
![]() $V)$
of
$V)$
of
![]() $\dot {b}\cap y$
. Since
$\dot {b}\cap y$
. Since
![]() $\dot {b}$
is thinly
$\dot {b}$
is thinly
![]() $\kappa $
-approximated in V by
$\kappa $
-approximated in V by
![]() $\mathbb {P}\ast \dot {\mathbb {Q}}$
, there
$\mathbb {P}\ast \dot {\mathbb {Q}}$
, there
![]() $<\kappa $
-many possible values for
$<\kappa $
-many possible values for
![]() $\dot {b}\cap y$
, and thus there will be
$\dot {b}\cap y$
, and thus there will be
![]() $<\kappa $
-many possible values in
$<\kappa $
-many possible values in
![]() $V[G]$
for
$V[G]$
for
![]() $\dot {b}\cap x$
. So
$\dot {b}\cap x$
. So
![]() $\dot {b}$
is thinly
$\dot {b}$
is thinly
![]() $\kappa $
-approximated by
$\kappa $
-approximated by
![]() $\mathbb {Q}$
over
$\mathbb {Q}$
over
![]() $V[G]$
.
$V[G]$
.
Lemma 2.10 (Part of Easton’s Lemma).
Let
![]() $\mathbb {P}$
be
$\mathbb {P}$
be
![]() $\kappa $
-closed in W, where V is a
$\kappa $
-closed in W, where V is a
![]() $\kappa $
-cc forcing extension of W. Then forcing with
$\kappa $
-cc forcing extension of W. Then forcing with
![]() $\mathbb {P}$
over V does not add any sequences of length
$\mathbb {P}$
over V does not add any sequences of length
![]() $<\kappa $
.
$<\kappa $
.
Lemma 2.11. Suppose that
![]() $\dot {b}$
is a
$\dot {b}$
is a
![]() $\mathbb {P} \ast \dot {\mathbb {Q}} \ast \dot {\mathbb {S}}$
-name for a subset of some ordinal
$\mathbb {P} \ast \dot {\mathbb {Q}} \ast \dot {\mathbb {S}}$
-name for a subset of some ordinal
![]() $\mu $
, which is
$\mu $
, which is
![]() $\kappa $
-approximated. If
$\kappa $
-approximated. If
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\kappa $
-cc, and
$\kappa $
-cc, and
![]() $\mathbb {Q}$
does not add sequences of length less than
$\mathbb {Q}$
does not add sequences of length less than
![]() $\kappa $
to
$\kappa $
to
![]() $V[\mathbb {P}]$
, then in
$V[\mathbb {P}]$
, then in
![]() $V[\mathbb {P} \ast \dot {\mathbb {Q}}]$
,
$V[\mathbb {P} \ast \dot {\mathbb {Q}}]$
,
![]() $\dot {b}$
is still
$\dot {b}$
is still
![]() $\kappa $
-approximated by
$\kappa $
-approximated by
![]() $\mathbb {S}$
.
$\mathbb {S}$
.
Proof Let
![]() $z \in (\mathcal {P}_\kappa (\mu ))^{V[\mathbb {P}\ast \dot {\mathbb {Q}}]}$
. Since
$z \in (\mathcal {P}_\kappa (\mu ))^{V[\mathbb {P}\ast \dot {\mathbb {Q}}]}$
. Since
![]() $\mathbb {Q}$
does not add sequences of length
$\mathbb {Q}$
does not add sequences of length
![]() $< \kappa $
,
$< \kappa $
,
![]() $z \in (\mathcal {P}_\kappa (\mu ))^{V[\mathbb {P}]}$
. By Lemma 2.9,
$z \in (\mathcal {P}_\kappa (\mu ))^{V[\mathbb {P}]}$
. By Lemma 2.9,
![]() $\Vdash _{\mathbb {Q}\ast \dot {\mathbb {S}}} z \cap \dot {b} \in V[\mathbb {P}]$
. We conclude that, working in
$\Vdash _{\mathbb {Q}\ast \dot {\mathbb {S}}} z \cap \dot {b} \in V[\mathbb {P}]$
. We conclude that, working in
![]() $V[\mathbb {P} \ast \dot {\mathbb {Q}}]$
,
$V[\mathbb {P} \ast \dot {\mathbb {Q}}]$
,
![]() $\Vdash _{\mathbb {S}} z \cap \dot {b} \in V[\mathbb {P}] \subseteq V[\mathbb {P}\ast \dot {\mathbb {Q}}]$
.
$\Vdash _{\mathbb {S}} z \cap \dot {b} \in V[\mathbb {P}] \subseteq V[\mathbb {P}\ast \dot {\mathbb {Q}}]$
.
To show that forcings have the (thin) approximation property, we will use the following lemmas, which generalize traditional branch preservation lemmas for trees.
Lemma 2.12 [Reference Unger17, Lemma 7.9].
Let
![]() $\tau < \kappa $
with
$\tau < \kappa $
with
![]() $2^\tau \geq \kappa $
. If
$2^\tau \geq \kappa $
. If
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\tau ^+$
-closed, then
$\tau ^+$
-closed, then
![]() $\mathbb {P}$
has the thin
$\mathbb {P}$
has the thin
![]() $\kappa $
-approximation property.
$\kappa $
-approximation property.
Lemma 2.13 [Reference Unger17, Lemma 7.8].
Let
![]() $\kappa $
be regular. Suppose
$\kappa $
be regular. Suppose
![]() $\mathbb {P}$
is a poset such that
$\mathbb {P}$
is a poset such that
![]() $\mathbb {P}\times \mathbb {P}$
is
$\mathbb {P}\times \mathbb {P}$
is
![]() $\kappa $
-cc. Then
$\kappa $
-cc. Then
![]() $\mathbb {P}$
has the
$\mathbb {P}$
has the
![]() $\kappa $
-approximation property.
$\kappa $
-approximation property.
The following definition and lemma provide a tool for verifying when the square of a poset has the
![]() $\kappa $
-cc in outer models.
$\kappa $
-cc in outer models.
Definition 2.14. Let
![]() $K\subseteq V$
be a model of a sufficiently large fragment of ZFC. We say that K has the
$K\subseteq V$
be a model of a sufficiently large fragment of ZFC. We say that K has the
![]() $<\delta $
-covering property with respect to V if for every
$<\delta $
-covering property with respect to V if for every
![]() $A \subseteq K$
in V with
$A \subseteq K$
in V with
![]() $|A|<\delta $
, there is some
$|A|<\delta $
, there is some
![]() $B \in K$
so that
$B \in K$
so that
![]() $K\models |B|<\delta $
and
$K\models |B|<\delta $
and
![]() $A \subseteq B$
.
$A \subseteq B$
.
Lemma 2.15 [Reference Neeman14, Claim 2.2].
Let
![]() $\delta < \kappa $
be regular cardinals, and suppose K is a model of some large enough fragment of ZFC that has the
$\delta < \kappa $
be regular cardinals, and suppose K is a model of some large enough fragment of ZFC that has the
![]() $<\kappa $
-covering property with respect to V. Suppose also that for all
$<\kappa $
-covering property with respect to V. Suppose also that for all
![]() $\gamma < \kappa $
,
$\gamma < \kappa $
,
![]() $K \models \gamma ^{<\delta } < \kappa $
. Let
$K \models \gamma ^{<\delta } < \kappa $
. Let
![]() $\mathbb {P}$
be a forcing notion in K whose conditions are functions of size
$\mathbb {P}$
be a forcing notion in K whose conditions are functions of size
![]() $<\delta $
in K. Then any family of size
$<\delta $
in K. Then any family of size
![]() $\kappa $
in V of conditions in
$\kappa $
in V of conditions in
![]() $\mathbb {P}$
can be refined to a family of the same size whose domains form a
$\mathbb {P}$
can be refined to a family of the same size whose domains form a
![]() $\Delta $
-system.
$\Delta $
-system.
We will also use the following lemma that generalizes [Reference Neeman14, Claim 2.4].
Lemma 2.16. Let
![]() $\mathbb {P}$
be a
$\mathbb {P}$
be a
![]() $\kappa $
-cc forcing and
$\kappa $
-cc forcing and
![]() $\mathbb {Q}$
be a
$\mathbb {Q}$
be a
![]() $\kappa $
-closed forcing. Suppose there exists
$\kappa $
-closed forcing. Suppose there exists
![]() $\tau < \kappa $
such that
$\tau < \kappa $
such that
![]() $2^\tau> \kappa $
. Then
$2^\tau> \kappa $
. Then
![]() $\mathbb {Q}$
has the thin
$\mathbb {Q}$
has the thin
![]() $\kappa ^+$
-approximation property over the generic extension by
$\kappa ^+$
-approximation property over the generic extension by
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
Proof Let
![]() $\lambda>\kappa $
be some ordinal, and let
$\lambda>\kappa $
be some ordinal, and let
![]() $\dot {d}$
be a
$\dot {d}$
be a
![]() $\mathbb {P}\times \mathbb {Q}$
-name for a subset of
$\mathbb {P}\times \mathbb {Q}$
-name for a subset of
![]() $\lambda $
that is thinly
$\lambda $
that is thinly
![]() $\kappa ^+$
-approximated by
$\kappa ^+$
-approximated by
![]() $\mathbb {Q}$
over the generic extension of V by
$\mathbb {Q}$
over the generic extension of V by
![]() $\mathbb {P}$
. Suppose that
$\mathbb {P}$
. Suppose that
![]() $1 \Vdash _{\mathbb {P}\times \mathbb {Q}} \dot {d}\notin V[\dot {G}_{\mathbb {P}}]$
, where
$1 \Vdash _{\mathbb {P}\times \mathbb {Q}} \dot {d}\notin V[\dot {G}_{\mathbb {P}}]$
, where
![]() $\dot {G}_{\mathbb {P}}$
is the canonical name for a generic of
$\dot {G}_{\mathbb {P}}$
is the canonical name for a generic of
![]() $\mathbb {P}$
. Let
$\mathbb {P}$
. Let
![]() $\delta \leq \tau $
be the least such that
$\delta \leq \tau $
be the least such that
![]() $2^\delta> \kappa $
. For each
$2^\delta> \kappa $
. For each
![]() $\sigma \in 2^{<\delta }$
we will build a triple
$\sigma \in 2^{<\delta }$
we will build a triple
![]() $(A_\sigma , q_\sigma , x_\sigma )$
where
$(A_\sigma , q_\sigma , x_\sigma )$
where
![]() $A_\sigma $
is a maximal antichain in
$A_\sigma $
is a maximal antichain in
![]() $\mathbb {P}$
,
$\mathbb {P}$
,
![]() $q_\sigma \in \mathbb {Q}$
, and
$q_\sigma \in \mathbb {Q}$
, and
![]() $x_\sigma \in (\mathcal {P}_{\kappa ^+}(\lambda ))^V$
, such that
$x_\sigma \in (\mathcal {P}_{\kappa ^+}(\lambda ))^V$
, such that
![]() $q_{\sigma '} \leq q_\sigma $
whenever
$q_{\sigma '} \leq q_\sigma $
whenever
![]() $\sigma '$
extends
$\sigma '$
extends
![]() $\sigma $
, and for all
$\sigma $
, and for all
![]() $\sigma \in 2^{<\delta }$
and all
$\sigma \in 2^{<\delta }$
and all
![]() $p \in A_\sigma $
,
$p \in A_\sigma $
,
![]() $(p,q_{\sigma ^\smallfrown 0})$
and
$(p,q_{\sigma ^\smallfrown 0})$
and
![]() $(p,q_{\sigma ^\smallfrown 1})$
force contradictory values for
$(p,q_{\sigma ^\smallfrown 1})$
force contradictory values for
![]() $\dot {d}\cap x_\sigma $
. Note that it suffices to consider
$\dot {d}\cap x_\sigma $
. Note that it suffices to consider
![]() $x_\sigma \in (\mathcal {P}_{\kappa ^+}(\lambda ))^V$
, since
$x_\sigma \in (\mathcal {P}_{\kappa ^+}(\lambda ))^V$
, since
![]() $(\mathcal {P}_{\kappa ^+}(\lambda ))^V$
is cofinal in
$(\mathcal {P}_{\kappa ^+}(\lambda ))^V$
is cofinal in
![]() $(\mathcal {P}_{\kappa ^+}(\lambda ))^{V[\mathbb {P}]}$
by the
$(\mathcal {P}_{\kappa ^+}(\lambda ))^{V[\mathbb {P}]}$
by the
![]() $\kappa $
-cc of
$\kappa $
-cc of
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
We will build this inductively, using the following claim.
Claim 2.17. For any
![]() $p \in \mathbb {P}$
and
$p \in \mathbb {P}$
and
![]() $q_0, q_1\in \mathbb {Q}$
, we can find
$q_0, q_1\in \mathbb {Q}$
, we can find
![]() $p' \leq p$
,
$p' \leq p$
,
![]() $q_0'\leq q_0$
,
$q_0'\leq q_0$
,
![]() $q_1'\leq q_1$
, and
$q_1'\leq q_1$
, and
![]() $x \in \mathcal {P}_\kappa (\lambda )$
such that
$x \in \mathcal {P}_\kappa (\lambda )$
such that
![]() $p'$
forces that
$p'$
forces that
![]() $q^{\prime }_0$
and
$q^{\prime }_0$
and
![]() $q^{\prime }_1$
force contradictory information about
$q^{\prime }_1$
force contradictory information about
![]() $\dot {d}\cap x$
.
$\dot {d}\cap x$
.
Proof Recall that
![]() $1 \Vdash _{\mathbb {P}\times \mathbb {Q}} \dot {d}\notin V[\dot {G}_{\mathbb {P}}].$
It follows that if
$1 \Vdash _{\mathbb {P}\times \mathbb {Q}} \dot {d}\notin V[\dot {G}_{\mathbb {P}}].$
It follows that if
![]() $G\times Q_0 \times Q_1$
is generic for
$G\times Q_0 \times Q_1$
is generic for
![]() $\mathbb {P}\times \mathbb {Q} \times \mathbb {Q}$
, the interpretations
$\mathbb {P}\times \mathbb {Q} \times \mathbb {Q}$
, the interpretations
![]() $\dot {d}_{G\times Q_0}$
and
$\dot {d}_{G\times Q_0}$
and
![]() $\dot {d}_{G\times Q_1}$
must not be equal. Thus there must be a pair of conditions
$\dot {d}_{G\times Q_1}$
must not be equal. Thus there must be a pair of conditions
![]() $(p^{\prime }_0,q_0') \leq (p,q_0)$
and
$(p^{\prime }_0,q_0') \leq (p,q_0)$
and
![]() $(p^{\prime }_1, q^{\prime }_1) \leq (p,q_1)$
such that
$(p^{\prime }_1, q^{\prime }_1) \leq (p,q_1)$
such that
![]() $(p^{\prime }_0,q_0') \in G\times Q_0$
and
$(p^{\prime }_0,q_0') \in G\times Q_0$
and
![]() $(p^{\prime }_1,q_1') \in G\times Q_1$
and the pair decides incompatible information about
$(p^{\prime }_1,q_1') \in G\times Q_1$
and the pair decides incompatible information about
![]() $\dot {d}\cap x$
for some
$\dot {d}\cap x$
for some
![]() $x \in \mathcal {P}_{\kappa ^+}(\lambda )$
. Since
$x \in \mathcal {P}_{\kappa ^+}(\lambda )$
. Since
![]() $p^{\prime }_0$
and
$p^{\prime }_0$
and
![]() $p^{\prime }_1$
are both in G, they are compatible. We set
$p^{\prime }_1$
are both in G, they are compatible. We set
![]() $p'$
to be a common extension of
$p'$
to be a common extension of
![]() $p^{\prime }_0$
and
$p^{\prime }_0$
and
![]() $p^{\prime }_1$
; the conclusion follows.
$p^{\prime }_1$
; the conclusion follows.
Let
![]() $q \in \mathbb {Q}$
. We wish to build
$q \in \mathbb {Q}$
. We wish to build
![]() $(A,q_0, q_1, x)$
where A is a maximal antichain in
$(A,q_0, q_1, x)$
where A is a maximal antichain in
![]() $\mathbb {P}$
,
$\mathbb {P}$
,
![]() $q_0, q_1 \leq q$
, and for all
$q_0, q_1 \leq q$
, and for all
![]() $p \in A$
, p forces that
$p \in A$
, p forces that
![]() $q_0$
and
$q_0$
and
![]() $q_1$
force contradictory information about
$q_1$
force contradictory information about
![]() $\dot {d}\cap x$
.
$\dot {d}\cap x$
.
For each
![]() $q \in \mathbb {Q}$
, we construct
$q \in \mathbb {Q}$
, we construct
![]() $(A, q_0, q_1, x)$
recursively. Set
$(A, q_0, q_1, x)$
recursively. Set
![]() $q_0^0 = q_0^1 = q$
and
$q_0^0 = q_0^1 = q$
and
![]() ${A_0 = \emptyset }$
. At successor stages
${A_0 = \emptyset }$
. At successor stages
![]() $\alpha +1$
we choose a new p incompatible with all conditions in our antichain-in-construction
$\alpha +1$
we choose a new p incompatible with all conditions in our antichain-in-construction
![]() $A_\alpha $
if such exists, then strengthen it to
$A_\alpha $
if such exists, then strengthen it to
![]() $p' \leq p$
so that there exist some
$p' \leq p$
so that there exist some
![]() $q^0_{\alpha +1} \leq q^0_\alpha $
,
$q^0_{\alpha +1} \leq q^0_\alpha $
,
![]() $q^1_{\alpha +1} \leq q^1_\alpha $
, and
$q^1_{\alpha +1} \leq q^1_\alpha $
, and
![]() $x_{\alpha +1}\supset x_\alpha $
as desired. We then define
$x_{\alpha +1}\supset x_\alpha $
as desired. We then define
![]() $A_{\alpha +1}$
to be
$A_{\alpha +1}$
to be
![]() $A_\alpha \cup \{p'\}$
. At limit stages
$A_\alpha \cup \{p'\}$
. At limit stages
![]() $\gamma $
, we take unions (for
$\gamma $
, we take unions (for
![]() $A_\gamma $
and
$A_\gamma $
and
![]() $x_\gamma $
) and lower bounds for
$x_\gamma $
) and lower bounds for
![]() $q^0_\gamma $
and
$q^0_\gamma $
and
![]() $q_\gamma ^1$
. Note that since
$q_\gamma ^1$
. Note that since
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\kappa $
-cc, this process will end at some
$\kappa $
-cc, this process will end at some
![]() $\gamma < \kappa $
, and so since
$\gamma < \kappa $
, and so since
![]() $\mathbb {Q}$
is
$\mathbb {Q}$
is
![]() $\kappa $
-closed we will always be able to take these lower bounds. This process gives
$\kappa $
-closed we will always be able to take these lower bounds. This process gives
![]() $(A, q_0, q_1, x)$
. Applying this construction repeatedly, we can build the binary tree structure as desired.
$(A, q_0, q_1, x)$
. Applying this construction repeatedly, we can build the binary tree structure as desired.
Now let
![]() $x = \bigcup _{\sigma \in 2^{<\delta }} x_\sigma .$
For each
$x = \bigcup _{\sigma \in 2^{<\delta }} x_\sigma .$
For each
![]() $f \in 2^\delta $
, by closure we can find
$f \in 2^\delta $
, by closure we can find
![]() $q^{\prime }_f$
such that
$q^{\prime }_f$
such that
![]() $q^{\prime }_f \leq q_{f\upharpoonright \alpha }$
for all
$q^{\prime }_f \leq q_{f\upharpoonright \alpha }$
for all
![]() $\alpha < \delta $
. Let G be generic for
$\alpha < \delta $
. Let G be generic for
![]() $\mathbb {P}$
. Since G is generic,
$\mathbb {P}$
. Since G is generic,
![]() $G \cap A_\sigma $
is nonempty for all
$G \cap A_\sigma $
is nonempty for all
![]() $\sigma $
. Working in
$\sigma $
. Working in
![]() $V[G]$
, we define
$V[G]$
, we define
![]() $q_f \leq q^{\prime }_f$
to be a refinement deciding
$q_f \leq q^{\prime }_f$
to be a refinement deciding
![]() $\dot {d}\cap x$
.
$\dot {d}\cap x$
.
We claim that if
![]() $f \neq g$
are elements of
$f \neq g$
are elements of
![]() $2^\delta $
, then
$2^\delta $
, then
![]() $q_f$
and
$q_f$
and
![]() $q_g$
force contradictory things about
$q_g$
force contradictory things about
![]() $\dot {d}\cap x$
. Let
$\dot {d}\cap x$
. Let
![]() $\alpha $
be the largest such that
$\alpha $
be the largest such that
![]() $f\upharpoonright \alpha = g\upharpoonright \alpha $
. Since
$f\upharpoonright \alpha = g\upharpoonright \alpha $
. Since
![]() $G \cap A_{f\upharpoonright \alpha }$
is nonempty,
$G \cap A_{f\upharpoonright \alpha }$
is nonempty,
![]() $q_{f\upharpoonright \alpha ^\smallfrown 0}$
and
$q_{f\upharpoonright \alpha ^\smallfrown 0}$
and
![]() $q_{f\upharpoonright \alpha ^\smallfrown 1}$
force contradictory information about
$q_{f\upharpoonright \alpha ^\smallfrown 1}$
force contradictory information about
![]() $x_{f\upharpoonright \alpha }\subseteq x$
. Since f extends one of these and g extends the other, we see that
$x_{f\upharpoonright \alpha }\subseteq x$
. Since f extends one of these and g extends the other, we see that
![]() $q_f$
must disagree with
$q_f$
must disagree with
![]() $q_g$
on
$q_g$
on
![]() $\dot {d}\cap x$
. Thus every
$\dot {d}\cap x$
. Thus every
![]() $q_f$
for
$q_f$
for
![]() $f\in 2^\delta $
forces a different value for
$f\in 2^\delta $
forces a different value for
![]() $\dot {d}\cap x$
, and so there must be at least
$\dot {d}\cap x$
, and so there must be at least
![]() $2^\delta> \kappa $
potential values for
$2^\delta> \kappa $
potential values for
![]() $\dot {d}\cap x$
. But since
$\dot {d}\cap x$
. But since
![]() $\dot {d}$
is thinly
$\dot {d}$
is thinly
![]() $\kappa ^+$
-approximated, there are fewer than
$\kappa ^+$
-approximated, there are fewer than
![]() $\kappa ^+$
potential values for
$\kappa ^+$
potential values for
![]() $\dot {d}$
, and thus for
$\dot {d}$
, and thus for
![]() $\dot {d}\cap x$
. This gives a contradiction.
$\dot {d}\cap x$
. This gives a contradiction.
At the successor of a singular strong limit cardinal, we have a similar lemma, a generalization of [Reference Magidor and Shelah11, Lemma 2.1]. The main difference is that we index the construction by
![]() $\nu ^{<\tau }$
instead of
$\nu ^{<\tau }$
instead of
![]() $2^{<\delta }$
. To prove this lemma we need a couple of claims, which expand on the splitting behavior described in Claim 2.17
$2^{<\delta }$
. To prove this lemma we need a couple of claims, which expand on the splitting behavior described in Claim 2.17
Claim 2.18. Suppose
![]() $\nu $
is a singular strong limit cardinal with cofinality
$\nu $
is a singular strong limit cardinal with cofinality
![]() $\tau $
, and let
$\tau $
, and let
![]() $\lambda \geq \nu ^+$
. Let
$\lambda \geq \nu ^+$
. Let
![]() $\mathbb {S}$
be a notion of forcing. Let
$\mathbb {S}$
be a notion of forcing. Let
![]() $\dot {d}$
be a
$\dot {d}$
be a
![]() $\mathbb {S}$
-name for a subset of
$\mathbb {S}$
-name for a subset of
![]() $\lambda $
that is thinly
$\lambda $
that is thinly
![]() $\nu ^+$
-approximated by
$\nu ^+$
-approximated by
![]() $\mathbb {S}$
over V, such that
$\mathbb {S}$
over V, such that
![]() $\dot {d}$
is forced not to be in V. Then for any
$\dot {d}$
is forced not to be in V. Then for any
![]() $s \in \mathbb {S}$
, there is a sequence
$s \in \mathbb {S}$
, there is a sequence
![]() $\langle s_\alpha \mid \alpha < \nu \rangle $
of conditions in
$\langle s_\alpha \mid \alpha < \nu \rangle $
of conditions in
![]() $\mathbb {S}$
and a set
$\mathbb {S}$
and a set
![]() $x \in \mathcal {P}_{\nu ^+}(\lambda )$
, such that
$x \in \mathcal {P}_{\nu ^+}(\lambda )$
, such that
![]() $s_\alpha \leq s$
for each
$s_\alpha \leq s$
for each
![]() $\alpha < \nu $
and each
$\alpha < \nu $
and each
![]() $s_\alpha $
decides a different value for
$s_\alpha $
decides a different value for
![]() $\dot {d}\cap x$
.
$\dot {d}\cap x$
.
Proof Fix
![]() $s \in \mathbb {S}$
. For
$s \in \mathbb {S}$
. For
![]() $x \in \mathcal {P}_{\nu ^+}(\lambda )$
, let
$x \in \mathcal {P}_{\nu ^+}(\lambda )$
, let
![]() $T(x)$
be the set of all
$T(x)$
be the set of all
![]() $y \subseteq x$
such that some
$y \subseteq x$
such that some
![]() $s' \leq s$
forces
$s' \leq s$
forces
![]() $\dot {d}\cap x = y$
. Since
$\dot {d}\cap x = y$
. Since
![]() $\dot {d}$
is thinly
$\dot {d}$
is thinly
![]() $\nu ^+$
-approximated,
$\nu ^+$
-approximated,
![]() $|T(x)| \leq \nu $
for all x. We wish to construct
$|T(x)| \leq \nu $
for all x. We wish to construct
![]() $x \in \mathcal {P}_{\nu ^+}(\lambda )$
such that
$x \in \mathcal {P}_{\nu ^+}(\lambda )$
such that
![]() $|T(x)| = \nu $
.
$|T(x)| = \nu $
.
Fix
![]() $x_0 \in \mathcal {P}_{\nu ^+}(\lambda )$
. We will build a
$x_0 \in \mathcal {P}_{\nu ^+}(\lambda )$
. We will build a
![]() $\subseteq $
-increasing sequence
$\subseteq $
-increasing sequence
![]() $\langle x_\alpha \mid \alpha < \nu \rangle $
such that for all
$\langle x_\alpha \mid \alpha < \nu \rangle $
such that for all
![]() $\alpha < \nu $
and all
$\alpha < \nu $
and all
![]() $y \in T(x_\alpha )$
, there are distinct
$y \in T(x_\alpha )$
, there are distinct
![]() $y_0$
and
$y_0$
and
![]() $y_1$
in
$y_1$
in
![]() $T(x_{\alpha +1})$
such that
$T(x_{\alpha +1})$
such that
![]() $y_0 \cap x_\alpha = y_1 \cap x_\alpha = y$
. We do so recursively.
$y_0 \cap x_\alpha = y_1 \cap x_\alpha = y$
. We do so recursively.
Fix
![]() $\alpha < \nu $
, and let
$\alpha < \nu $
, and let
![]() $y \in T(x_\alpha )$
as witnessed by a condition
$y \in T(x_\alpha )$
as witnessed by a condition
![]() $s' \leq s$
. Since
$s' \leq s$
. Since
![]() $\dot {d}$
is forced not to be in V, we can find a set
$\dot {d}$
is forced not to be in V, we can find a set
![]() $x_{\alpha +1}^y \supseteq x_\alpha $
, distinct
$x_{\alpha +1}^y \supseteq x_\alpha $
, distinct
![]() $y^{\prime }_0, y^{\prime }_1 \in \mathcal {P}_{\nu ^+}(\lambda )$
, and conditions
$y^{\prime }_0, y^{\prime }_1 \in \mathcal {P}_{\nu ^+}(\lambda )$
, and conditions
![]() $s_0, s_1 \leq s'$
such that
$s_0, s_1 \leq s'$
such that
![]() $s_0 \Vdash \dot {d}\cap x_{\alpha +1}^y = y^{\prime }_0$
and
$s_0 \Vdash \dot {d}\cap x_{\alpha +1}^y = y^{\prime }_0$
and
![]() $s_1 \Vdash \dot {d}\cap x_{\alpha +1}^y = y^{\prime }_1$
. (If such objects did not exist, then a single condition could decide
$s_1 \Vdash \dot {d}\cap x_{\alpha +1}^y = y^{\prime }_1$
. (If such objects did not exist, then a single condition could decide
![]() $\dot {d}$
, contradicting the assumption that
$\dot {d}$
, contradicting the assumption that
![]() $\dot {d} \notin V$
.) Since
$\dot {d} \notin V$
.) Since
![]() $s_0$
and
$s_0$
and
![]() $s_1$
extend
$s_1$
extend
![]() $s'$
, we must have
$s'$
, we must have
![]() $y^{\prime }_0 \cap x_\alpha = y^{\prime }_1 \cap x_\alpha = y$
. Let
$y^{\prime }_0 \cap x_\alpha = y^{\prime }_1 \cap x_\alpha = y$
. Let
![]() $x_{\alpha +1} = \bigcup _{y \in T(x_\alpha )} x_{\alpha +1}^y$
. For each
$x_{\alpha +1} = \bigcup _{y \in T(x_\alpha )} x_{\alpha +1}^y$
. For each
![]() $y \in T(x_\alpha )$
, let
$y \in T(x_\alpha )$
, let
![]() $s_0$
,
$s_0$
,
![]() $s_1$
,
$s_1$
,
![]() $y^{\prime }_0$
, and
$y^{\prime }_0$
, and
![]() $y^{\prime }_1$
be as above. Extend
$y^{\prime }_1$
be as above. Extend
![]() $s_0$
to decide the value of
$s_0$
to decide the value of
![]() $\dot {d}\cap x_{\alpha +1}$
to be some
$\dot {d}\cap x_{\alpha +1}$
to be some
![]() $y_0 \supseteq y^{\prime }_0$
; similarly, extend
$y_0 \supseteq y^{\prime }_0$
; similarly, extend
![]() $s_1$
to force
$s_1$
to force
![]() $\dot {d}\cap x_{\alpha +1} = y_1$
for some
$\dot {d}\cap x_{\alpha +1} = y_1$
for some
![]() $y_1 \supseteq y^{\prime }_1$
. Then
$y_1 \supseteq y^{\prime }_1$
. Then
![]() $y_0$
and
$y_0$
and
![]() $y_1$
are distinct elements of
$y_1$
are distinct elements of
![]() $T(x_{\alpha +1})$
, and
$T(x_{\alpha +1})$
, and
![]() $y_0\cap x_\alpha = y_1\cap x_\alpha = y$
, so
$y_0\cap x_\alpha = y_1\cap x_\alpha = y$
, so
![]() $x_{\alpha +1}$
has the desired properties. This covers successor stages; at limit stages we take unions.
$x_{\alpha +1}$
has the desired properties. This covers successor stages; at limit stages we take unions.
Now let
![]() $x = \bigcup _{\alpha < \nu } x_\alpha $
. Let
$x = \bigcup _{\alpha < \nu } x_\alpha $
. Let
![]() $y \in T(x)$
. Then for all
$y \in T(x)$
. Then for all
![]() $\alpha < \nu $
,
$\alpha < \nu $
,
![]() $y\cap x_\alpha \in T(x_\alpha )$
. By construction, we have distinct
$y\cap x_\alpha \in T(x_\alpha )$
. By construction, we have distinct
![]() $y_0$
and
$y_0$
and
![]() $y_1$
in
$y_1$
in
![]() $T(x_\alpha +1)$
(as witnessed by conditions
$T(x_\alpha +1)$
(as witnessed by conditions
![]() $s_0$
and
$s_0$
and
![]() $s_1$
) such that
$s_1$
) such that
![]() $y_0 \cap x_\alpha = y_1 \cap x_\alpha = y\cap x_\alpha $
. Moreover, any extensions of these conditions that decide
$y_0 \cap x_\alpha = y_1 \cap x_\alpha = y\cap x_\alpha $
. Moreover, any extensions of these conditions that decide
![]() $\dot {d}\cap x$
must decide incompatible values. Since there are
$\dot {d}\cap x$
must decide incompatible values. Since there are
![]() $\nu $
-many of these splittings, there must be at least
$\nu $
-many of these splittings, there must be at least
![]() $\nu $
possible values for
$\nu $
possible values for
![]() $\dot {d}\cap x$
. We conclude that
$\dot {d}\cap x$
. We conclude that
![]() $|T(x)| = \nu $
.
$|T(x)| = \nu $
.
Claim 2.19. Suppose
![]() $\nu $
is a singular strong limit cardinal with cofinality
$\nu $
is a singular strong limit cardinal with cofinality
![]() $\tau $
, and let
$\tau $
, and let
![]() $\lambda \geq \nu ^+$
. Let
$\lambda \geq \nu ^+$
. Let
![]() $\mathbb {P}$
and
$\mathbb {P}$
and
![]() $\mathbb {Q}$
be notions of forcing such that
$\mathbb {Q}$
be notions of forcing such that
![]() $|\mathbb {P}|\leq \mu $
and
$|\mathbb {P}|\leq \mu $
and
![]() $\mathbb {Q}$
is
$\mathbb {Q}$
is
![]() $\mu ^+$
-closed for some
$\mu ^+$
-closed for some
![]() $\mu $
with
$\mu $
with
![]() $\tau < \mu < \nu $
. Let
$\tau < \mu < \nu $
. Let
![]() $\dot {d}$
be a
$\dot {d}$
be a
![]() $\mathbb {P}\times \mathbb {Q}$
-name for a subset of
$\mathbb {P}\times \mathbb {Q}$
-name for a subset of
![]() $\lambda $
that is thinly
$\lambda $
that is thinly
![]() $\nu ^+$
-approximated by
$\nu ^+$
-approximated by
![]() $\mathbb {Q}$
over the generic extension of V by
$\mathbb {Q}$
over the generic extension of V by
![]() $\mathbb {P}$
, such that
$\mathbb {P}$
, such that
![]() $1_{\mathbb {P}\times \mathbb {Q}} \Vdash \dot {d}\notin V[\dot {G}_{\mathbb {P}}]$
.
$1_{\mathbb {P}\times \mathbb {Q}} \Vdash \dot {d}\notin V[\dot {G}_{\mathbb {P}}]$
.
Suppose
![]() $p_0 \in \mathbb {P}$
, and let
$p_0 \in \mathbb {P}$
, and let
![]() $\langle q_\alpha \mid \alpha < \nu \rangle $
be a sequence of conditions in
$\langle q_\alpha \mid \alpha < \nu \rangle $
be a sequence of conditions in
![]() $\mathbb {Q}$
. Then there is a sequence
$\mathbb {Q}$
. Then there is a sequence
![]() $\langle q^{\prime }_\alpha \mid \alpha < \nu \rangle $
with
$\langle q^{\prime }_\alpha \mid \alpha < \nu \rangle $
with
![]() $q^{\prime }_\alpha \leq q_\alpha $
for each
$q^{\prime }_\alpha \leq q_\alpha $
for each
![]() $\alpha < \nu $
, along with a set
$\alpha < \nu $
, along with a set
![]() $x \in \mathcal {P}_{\nu ^+}(\lambda )$
, such that for all
$x \in \mathcal {P}_{\nu ^+}(\lambda )$
, such that for all
![]() $\alpha < \beta $
there is some
$\alpha < \beta $
there is some
![]() $p_{\alpha \beta } \leq p_0$
so that
$p_{\alpha \beta } \leq p_0$
so that
![]() $(p_{\alpha \beta },q^{\prime }_\alpha )$
and
$(p_{\alpha \beta },q^{\prime }_\alpha )$
and
![]() $(p_{\alpha \beta }, q^{\prime }_\beta $
) force incompatible information about
$(p_{\alpha \beta }, q^{\prime }_\beta $
) force incompatible information about
![]() $\dot {d}\cap x$
.
$\dot {d}\cap x$
.
Proof Let G be generic for
![]() $\mathbb {P}$
containing
$\mathbb {P}$
containing
![]() $p_0$
, and work for the moment in
$p_0$
, and work for the moment in
![]() $V[G]$
. For all
$V[G]$
. For all
![]() $\alpha < \nu $
, by Claim 2.18 there is
$\alpha < \nu $
, by Claim 2.18 there is
![]() $x_\alpha \in \mathcal {P}_{\nu ^+}(\lambda )$
such that there are
$x_\alpha \in \mathcal {P}_{\nu ^+}(\lambda )$
such that there are
![]() $\nu $
-many possible values for
$\nu $
-many possible values for
![]() $\dot {d}\cap x_\alpha $
that can be forced by extensions of
$\dot {d}\cap x_\alpha $
that can be forced by extensions of
![]() $q_\alpha $
. Returning to V, we note that these possible values are also possible values of
$q_\alpha $
. Returning to V, we note that these possible values are also possible values of
![]() $\dot {d}\cap x_\alpha $
that can be forced by extensions of
$\dot {d}\cap x_\alpha $
that can be forced by extensions of
![]() $(p_0, q_\alpha )$
. Since
$(p_0, q_\alpha )$
. Since
![]() $\mathbb {P}$
does not collapse
$\mathbb {P}$
does not collapse
![]() $\nu $
or
$\nu $
or
![]() $\nu ^+$
, we conclude that (in V) there are
$\nu ^+$
, we conclude that (in V) there are
![]() $\nu $
-many possibilities for
$\nu $
-many possibilities for
![]() $\dot {d}\cap x_\alpha $
that can be forced by extensions of
$\dot {d}\cap x_\alpha $
that can be forced by extensions of
![]() $(p_0, q_\alpha )$
.
$(p_0, q_\alpha )$
.
Let
![]() $x = \bigcup _{\alpha < \nu } x_\alpha $
; note that
$x = \bigcup _{\alpha < \nu } x_\alpha $
; note that
![]() $x \in \mathcal {P}_{\nu ^+}(\lambda )$
. Since
$x \in \mathcal {P}_{\nu ^+}(\lambda )$
. Since
![]() $(p_0,q_\alpha )$
has
$(p_0,q_\alpha )$
has
![]() $\nu $
-many extensions deciding pairwise-distinct values for
$\nu $
-many extensions deciding pairwise-distinct values for
![]() $\dot {d}\cap x_\alpha $
, by extending each further we can obtain
$\dot {d}\cap x_\alpha $
, by extending each further we can obtain
![]() $\nu $
-many extensions of each
$\nu $
-many extensions of each
![]() $(p_0, q_\alpha )$
deciding pairwise-distinct values for
$(p_0, q_\alpha )$
deciding pairwise-distinct values for
![]() $\dot {d}\cap x$
. (To do this, simply take the
$\dot {d}\cap x$
. (To do this, simply take the
![]() $\nu $
-many extensions that disagree on
$\nu $
-many extensions that disagree on
![]() $\dot {d}\cap x_\alpha $
, and extend them further to decide
$\dot {d}\cap x_\alpha $
, and extend them further to decide
![]() $\dot {d}\cap x$
. Since
$\dot {d}\cap x$
. Since
![]() $x_\alpha \subseteq x$
, these further extensions must also disagree on
$x_\alpha \subseteq x$
, these further extensions must also disagree on
![]() $\dot {d}\cap x$
.)
$\dot {d}\cap x$
.)
For all
![]() $\alpha < \nu $
, we will inductively define a condition
$\alpha < \nu $
, we will inductively define a condition
![]() $q^{\prime }_\alpha \leq q_\alpha $
and functions
$q^{\prime }_\alpha \leq q_\alpha $
and functions
![]() $e_\alpha :\mathbb {P}\to \mathbb {P}$
and
$e_\alpha :\mathbb {P}\to \mathbb {P}$
and
![]() $f_\alpha :\mathbb {P}\to \mathcal {P}(x)$
such that the following hold:
$f_\alpha :\mathbb {P}\to \mathcal {P}(x)$
such that the following hold:
-
•
 $e_\alpha (p) \leq p.$
$e_\alpha (p) \leq p.$
-
•
 $(e_\alpha (p), q^{\prime }_\alpha )\Vdash _{\mathbb {P}\times \mathbb {Q}} \dot {d}\cap x = f_\alpha (p).$
$(e_\alpha (p), q^{\prime }_\alpha )\Vdash _{\mathbb {P}\times \mathbb {Q}} \dot {d}\cap x = f_\alpha (p).$
-
• For all
 $\alpha < \beta < \nu $
,
$\alpha < \beta < \nu $
,
 $f_\alpha (p) \neq f_\beta (p_0)$
for all
$f_\alpha (p) \neq f_\beta (p_0)$
for all
 $p\in \mathbb {P}$
.
$p\in \mathbb {P}$
.
The sequence
![]() $\langle q^{\prime }_\alpha \mid \alpha < \nu \rangle $
will be the desired object; for each pair
$\langle q^{\prime }_\alpha \mid \alpha < \nu \rangle $
will be the desired object; for each pair
![]() $\alpha < \beta $
we will choose
$\alpha < \beta $
we will choose
![]() $p_{\alpha \beta }$
to be
$p_{\alpha \beta }$
to be
![]() $e_\alpha (e_\beta (p_0))$
. We build these objects with a double induction, inducting over both
$e_\alpha (e_\beta (p_0))$
. We build these objects with a double induction, inducting over both
![]() $\alpha $
and the elements of
$\alpha $
and the elements of
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
Enumerate
![]() $\mathbb {P}$
by
$\mathbb {P}$
by
![]() $\langle p_\xi \mid \xi < \mu \rangle $
, starting with the already determined condition
$\langle p_\xi \mid \xi < \mu \rangle $
, starting with the already determined condition
![]() $p_0$
. Suppose we have defined
$p_0$
. Suppose we have defined
![]() $q^{\prime }_\delta , e_\delta ,$
and
$q^{\prime }_\delta , e_\delta ,$
and
![]() $f_\delta $
for all
$f_\delta $
for all
![]() $\delta < \alpha $
. Inducting on
$\delta < \alpha $
. Inducting on
![]() $\xi $
, we wish to define
$\xi $
, we wish to define
![]() $q_\alpha ^\xi \leq q_\alpha $
,
$q_\alpha ^\xi \leq q_\alpha $
,
![]() $e_\alpha (p_\xi ) \leq p_\xi $
, and
$e_\alpha (p_\xi ) \leq p_\xi $
, and
![]() $f_\alpha (p_\xi )$
such that:
$f_\alpha (p_\xi )$
such that:
-
•
 $\langle q_\alpha ^\xi \mid \xi < \mu \rangle $
forms a decreasing sequence below
$\langle q_\alpha ^\xi \mid \xi < \mu \rangle $
forms a decreasing sequence below
 $q_\alpha $
,
$q_\alpha $
, -
•
 $(e_\alpha (p_\xi ), q_\alpha ^\xi )\Vdash _{\mathbb {P}\times \mathbb {Q}}\dot {d}\cap x = f_\alpha (p_\xi )$
, and
$(e_\alpha (p_\xi ), q_\alpha ^\xi )\Vdash _{\mathbb {P}\times \mathbb {Q}}\dot {d}\cap x = f_\alpha (p_\xi )$
, and -
•
 $f_\delta (p) \neq f_\alpha (p_0)$
for all
$f_\delta (p) \neq f_\alpha (p_0)$
for all
 $\delta < \alpha $
and all
$\delta < \alpha $
and all
 $p \in \mathbb {P}$
.
$p \in \mathbb {P}$
.
Since
![]() $(p_0, q)$
has
$(p_0, q)$
has
![]() $\nu $
-many extensions deciding
$\nu $
-many extensions deciding
![]() $\dot {d}\cap x$
differently, and we have used at most
$\dot {d}\cap x$
differently, and we have used at most
![]() $\max (\alpha , |\mathbb {P}|) < \nu $
of these extensions in earlier stages, we can pick
$\max (\alpha , |\mathbb {P}|) < \nu $
of these extensions in earlier stages, we can pick
![]() $e_\alpha (p_0), q_\alpha ^0,$
and
$e_\alpha (p_0), q_\alpha ^0,$
and
![]() $f_\alpha (p_0)$
as desired. At successor stages
$f_\alpha (p_0)$
as desired. At successor stages
![]() $\xi +1$
, we choose an extension
$\xi +1$
, we choose an extension
![]() $(e_\alpha (p_{\xi +1}), q_\alpha ^{\xi +1})$
of
$(e_\alpha (p_{\xi +1}), q_\alpha ^{\xi +1})$
of
![]() $(p_{\xi +1}, q_\alpha ^\xi )$
deciding the value of
$(p_{\xi +1}, q_\alpha ^\xi )$
deciding the value of
![]() $\dot {d}\cap x$
, and set
$\dot {d}\cap x$
, and set
![]() $f_\alpha (p_{\xi +1})$
to be that value. At limit stages
$f_\alpha (p_{\xi +1})$
to be that value. At limit stages
![]() $\gamma $
, using the
$\gamma $
, using the
![]() $\mu ^+$
-closure of
$\mu ^+$
-closure of
![]() $\mathbb {Q}$
we select
$\mathbb {Q}$
we select
![]() $e_\alpha (p_\gamma ) \leq p_\gamma $
and a lower bound
$e_\alpha (p_\gamma ) \leq p_\gamma $
and a lower bound
![]() $q_\alpha ^{\gamma }$
of
$q_\alpha ^{\gamma }$
of
![]() $\langle q_\alpha ^\xi \mid \xi < \gamma \rangle $
, such that
$\langle q_\alpha ^\xi \mid \xi < \gamma \rangle $
, such that
![]() $(e_\alpha (p_\gamma ), q_\alpha ^\gamma )$
decides the value of
$(e_\alpha (p_\gamma ), q_\alpha ^\gamma )$
decides the value of
![]() $\dot {d}\cap x$
. Set
$\dot {d}\cap x$
. Set
![]() $f_\alpha (p_{\gamma })$
to be this value. When this induction on the elements of
$f_\alpha (p_{\gamma })$
to be this value. When this induction on the elements of
![]() $\mathbb {P}$
is finished, we define
$\mathbb {P}$
is finished, we define
![]() $q^{\prime }_\alpha $
to be a lower bound of
$q^{\prime }_\alpha $
to be a lower bound of
![]() $\langle q_\alpha ^\xi \mid \xi < \mu \rangle $
. This process constructs functions
$\langle q_\alpha ^\xi \mid \xi < \mu \rangle $
. This process constructs functions
![]() $e_\alpha $
and
$e_\alpha $
and
![]() $f_\alpha $
, as well as the sequence
$f_\alpha $
, as well as the sequence
![]() $\langle q^{\prime }_\alpha \mid \alpha < \nu \rangle $
, with the desired properties.
$\langle q^{\prime }_\alpha \mid \alpha < \nu \rangle $
, with the desired properties.
Finally we verify that the sequence
![]() $\langle q^{\prime }_\alpha \mid \alpha < \nu \rangle $
meets the requirements in the statement of the lemma. Fix
$\langle q^{\prime }_\alpha \mid \alpha < \nu \rangle $
meets the requirements in the statement of the lemma. Fix
![]() $\alpha < \beta < \nu $
. Let
$\alpha < \beta < \nu $
. Let
![]() $p_{\alpha \beta } = e_\alpha (e_\beta (p_0))$
. By construction,
$p_{\alpha \beta } = e_\alpha (e_\beta (p_0))$
. By construction,
![]() $e_\beta (p_0)\Vdash \dot {d}\cap x = f_\beta (p_0)$
; since
$e_\beta (p_0)\Vdash \dot {d}\cap x = f_\beta (p_0)$
; since
![]() $p_{\alpha \beta } \leq e_\beta (p_0)$
,
$p_{\alpha \beta } \leq e_\beta (p_0)$
,
![]() $(p_{\alpha \beta }, q^{\prime }_\beta )$
also forces this. On the other hand,
$(p_{\alpha \beta }, q^{\prime }_\beta )$
also forces this. On the other hand,
![]() $(p_{\alpha \beta }, q^{\prime }_\alpha )\Vdash \dot {d}\cap x = f_\alpha (e_\beta (p_0))$
. By construction, these must be different values.
$(p_{\alpha \beta }, q^{\prime }_\alpha )\Vdash \dot {d}\cap x = f_\alpha (e_\beta (p_0))$
. By construction, these must be different values.
Lemma 2.20. Suppose
![]() $\nu $
is a singular strong limit cardinal with cofinality
$\nu $
is a singular strong limit cardinal with cofinality
![]() $\tau $
. Let
$\tau $
. Let
![]() $\mathbb {Q}$
be a
$\mathbb {Q}$
be a
![]() $\mu ^+$
-closed forcing over a model V for some
$\mu ^+$
-closed forcing over a model V for some
![]() $\mu < \nu $
with
$\mu < \nu $
with
![]() $\tau \leq \mu $
, and let
$\tau \leq \mu $
, and let
![]() $\mathbb {P} \in V$
be a poset with
$\mathbb {P} \in V$
be a poset with
![]() $|\mathbb {P}|\leq \mu $
. Then
$|\mathbb {P}|\leq \mu $
. Then
![]() $\mathbb {Q}$
has the thin
$\mathbb {Q}$
has the thin
![]() $\nu ^+$
-approximation property in the generic extension of V by
$\nu ^+$
-approximation property in the generic extension of V by
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
Proof Let
![]() $\lambda $
be a some ordinal, and let
$\lambda $
be a some ordinal, and let
![]() $\dot {d}$
be a
$\dot {d}$
be a
![]() $\mathbb {P}\times \mathbb {Q}$
-name for a subset of
$\mathbb {P}\times \mathbb {Q}$
-name for a subset of
![]() $\lambda $
that is thinly
$\lambda $
that is thinly
![]() $\nu ^+$
-approximated by
$\nu ^+$
-approximated by
![]() $\mathbb {Q}$
over the generic extension by
$\mathbb {Q}$
over the generic extension by
![]() $\mathbb {P}$
. Suppose further that the empty condition in
$\mathbb {P}$
. Suppose further that the empty condition in
![]() $\mathbb {P}\times \mathbb {Q}$
forces
$\mathbb {P}\times \mathbb {Q}$
forces
![]() $\dot {d}\notin V[\dot {G}_{\mathbb {P}}]$
. For each
$\dot {d}\notin V[\dot {G}_{\mathbb {P}}]$
. For each
![]() $\sigma \in \nu ^{<\tau }$
we will build a pair
$\sigma \in \nu ^{<\tau }$
we will build a pair
![]() $(q_\sigma , x_\sigma )$
with
$(q_\sigma , x_\sigma )$
with
![]() $q_\sigma \in \mathbb {Q}$
and
$q_\sigma \in \mathbb {Q}$
and
![]() $x_\sigma \in (\mathcal {P}_{\nu ^+}(\lambda ))^V$
, along with a collection of dense sets
$x_\sigma \in (\mathcal {P}_{\nu ^+}(\lambda ))^V$
, along with a collection of dense sets
![]() $\langle D_\sigma ^{\alpha \beta }\mid \alpha < \beta < \nu \rangle $
, such that
$\langle D_\sigma ^{\alpha \beta }\mid \alpha < \beta < \nu \rangle $
, such that
![]() $q_{\sigma '} \leq q_\sigma $
whenever
$q_{\sigma '} \leq q_\sigma $
whenever
![]() $\sigma '$
extends
$\sigma '$
extends
![]() $\sigma $
, and for all
$\sigma $
, and for all
![]() $\sigma \in \nu ^{<\tau }$
, all
$\sigma \in \nu ^{<\tau }$
, all
![]() $\alpha < \beta $
, and all
$\alpha < \beta $
, and all
![]() $p \in D^{\alpha \beta }_{\sigma }$
,
$p \in D^{\alpha \beta }_{\sigma }$
,
![]() $(p, q_{\sigma ^\smallfrown \alpha })$
and
$(p, q_{\sigma ^\smallfrown \alpha })$
and
![]() $(p, q_{\sigma ^\smallfrown \beta })$
force contradictory information about
$(p, q_{\sigma ^\smallfrown \beta })$
force contradictory information about
![]() $\dot {d}\cap x_{\sigma }$
.
$\dot {d}\cap x_{\sigma }$
.
Fix
![]() $q \in \mathbb {Q}$
. We will construct
$q \in \mathbb {Q}$
. We will construct
![]() $\langle q_\alpha \mid \alpha < \nu \rangle , x \in \mathcal {P}_{\nu ^+}(\lambda )$
, and a dense sets
$\langle q_\alpha \mid \alpha < \nu \rangle , x \in \mathcal {P}_{\nu ^+}(\lambda )$
, and a dense sets
![]() $D_{\alpha \beta }$
, such that each
$D_{\alpha \beta }$
, such that each
![]() $q_\alpha \leq q$
, and for all
$q_\alpha \leq q$
, and for all
![]() $\alpha < \beta $
and all
$\alpha < \beta $
and all
![]() $p \in D_{\alpha \beta }$
, p forces that
$p \in D_{\alpha \beta }$
, p forces that
![]() $q_\alpha $
and
$q_\alpha $
and
![]() $q_\beta $
force contradictory information about
$q_\beta $
force contradictory information about
![]() $\dot {d}\cap x$
.
$\dot {d}\cap x$
.
We do so by recursion, iterating over all elements of
![]() $\mathbb {P}$
. Enumerate the elements of
$\mathbb {P}$
. Enumerate the elements of
![]() $\mathbb {P}$
by
$\mathbb {P}$
by
![]() $\langle p_\delta \mid \delta < \mu \rangle $
. Set
$\langle p_\delta \mid \delta < \mu \rangle $
. Set
![]() $D_{\alpha \beta }^0 = \emptyset $
, and for all
$D_{\alpha \beta }^0 = \emptyset $
, and for all
![]() $\alpha < \nu $
, let
$\alpha < \nu $
, let
![]() $q_\alpha ^0 = q$
. First we consider the successor stage
$q_\alpha ^0 = q$
. First we consider the successor stage
![]() $\delta +1$
. Applying Claim 2.19 to
$\delta +1$
. Applying Claim 2.19 to
![]() $p_{\delta }$
and the sequence
$p_{\delta }$
and the sequence
![]() $\langle q^\delta _\alpha \mid \alpha < \nu \rangle $
, we obtain
$\langle q^\delta _\alpha \mid \alpha < \nu \rangle $
, we obtain
![]() $\langle q^{\delta +1}_\alpha \mid \alpha < \nu \rangle $
with
$\langle q^{\delta +1}_\alpha \mid \alpha < \nu \rangle $
with
![]() $q^{\delta +1}_\alpha \leq q^\delta _\alpha $
for each
$q^{\delta +1}_\alpha \leq q^\delta _\alpha $
for each
![]() $\alpha < \nu $
,
$\alpha < \nu $
,
![]() $x_{\delta +1} \in \mathcal {P}_{\nu ^+}(\lambda )$
, and strengthenings
$x_{\delta +1} \in \mathcal {P}_{\nu ^+}(\lambda )$
, and strengthenings
![]() $p_{\alpha \beta }^{\delta } \leq p_{\delta }$
for all
$p_{\alpha \beta }^{\delta } \leq p_{\delta }$
for all
![]() $\alpha < \beta < \nu $
, so that
$\alpha < \beta < \nu $
, so that
![]() $(p_{\alpha \beta }^{\delta }, q^{\delta +1}_\alpha )$
and
$(p_{\alpha \beta }^{\delta }, q^{\delta +1}_\alpha )$
and
![]() $(p_{\alpha \beta }^{\delta }, q^{\delta +1}_\beta )$
force contradictory information about
$(p_{\alpha \beta }^{\delta }, q^{\delta +1}_\beta )$
force contradictory information about
![]() $\dot {d}\cap x_{\delta +1}$
. We set
$\dot {d}\cap x_{\delta +1}$
. We set
![]() $D_{\alpha \beta }^{\delta +1} = D_{\alpha \beta }^\delta \cup \{p_{\alpha \beta }^{\delta }\}$
.
$D_{\alpha \beta }^{\delta +1} = D_{\alpha \beta }^\delta \cup \{p_{\alpha \beta }^{\delta }\}$
.
At each limit stage
![]() $\gamma $
, we take unions for
$\gamma $
, we take unions for
![]() $x_\gamma $
and each
$x_\gamma $
and each
![]() $D_{\alpha \beta }^\gamma $
, and lower bounds to produce each
$D_{\alpha \beta }^\gamma $
, and lower bounds to produce each
![]() $q^\gamma _\alpha $
. Since
$q^\gamma _\alpha $
. Since
![]() $\mathbb {Q}$
is
$\mathbb {Q}$
is
![]() $\mu ^+$
-closed, we will always be able to take these lower bounds. Let
$\mu ^+$
-closed, we will always be able to take these lower bounds. Let
![]() $q_\alpha $
be a lower bound of the sequence
$q_\alpha $
be a lower bound of the sequence
![]() $\langle q^\delta _\alpha \mid \delta < \mu \rangle $
. Finally, setting
$\langle q^\delta _\alpha \mid \delta < \mu \rangle $
. Finally, setting
![]() $x = \bigcup _{\delta <\mu }x_\delta $
, we obtain the desired objects. Repeating this construction, we can obtain
$x = \bigcup _{\delta <\mu }x_\delta $
, we obtain the desired objects. Repeating this construction, we can obtain
![]() $(q_\sigma , x_\sigma )$
and
$(q_\sigma , x_\sigma )$
and
![]() $\langle D_\sigma ^{\alpha \beta }\mid \alpha < \beta <\nu \rangle $
as desired for any
$\langle D_\sigma ^{\alpha \beta }\mid \alpha < \beta <\nu \rangle $
as desired for any
![]() $\sigma \in \nu ^{<\tau }$
and any
$\sigma \in \nu ^{<\tau }$
and any
![]() $\alpha < \beta < \nu $
.
$\alpha < \beta < \nu $
.
Let
![]() $x = \bigcup _{\sigma \in \nu ^{<\tau }} x_\sigma $
. For all
$x = \bigcup _{\sigma \in \nu ^{<\tau }} x_\sigma $
. For all
![]() $f \in \nu ^\tau $
, by the closure of
$f \in \nu ^\tau $
, by the closure of
![]() $\mathbb {Q}$
we can find
$\mathbb {Q}$
we can find
![]() $q^{\prime }_f$
such that
$q^{\prime }_f$
such that
![]() $q^{\prime }_f\leq q_{f\upharpoonright \alpha }$
for all
$q^{\prime }_f\leq q_{f\upharpoonright \alpha }$
for all
![]() $\alpha <\tau $
. Let G be generic for
$\alpha <\tau $
. Let G be generic for
![]() $\mathbb {P}$
, and note that it will intersect every
$\mathbb {P}$
, and note that it will intersect every
![]() $D^{\alpha \beta }_{\sigma }$
. Working in
$D^{\alpha \beta }_{\sigma }$
. Working in
![]() $V[G]$
, let
$V[G]$
, let
![]() $q_f \leq q_f'$
be a strengthening that decides
$q_f \leq q_f'$
be a strengthening that decides
![]() $\dot {d}\cap x$
.
$\dot {d}\cap x$
.
Let
![]() $f \neq g$
be elements of
$f \neq g$
be elements of
![]() $\nu ^\tau $
, and let
$\nu ^\tau $
, and let
![]() $\alpha $
be the largest such that
$\alpha $
be the largest such that
![]() $f\upharpoonright \alpha = g\upharpoonright \alpha $
. Let
$f\upharpoonright \alpha = g\upharpoonright \alpha $
. Let
![]() $\zeta = f(\alpha )$
, and
$\zeta = f(\alpha )$
, and
![]() $\xi = g(\alpha )$
. Since G intersects
$\xi = g(\alpha )$
. Since G intersects
![]() $D^{\zeta \xi }_{f\upharpoonright \alpha }$
, we see that
$D^{\zeta \xi }_{f\upharpoonright \alpha }$
, we see that
![]() $q_{(f\upharpoonright \alpha ) ^\smallfrown \zeta }$
and
$q_{(f\upharpoonright \alpha ) ^\smallfrown \zeta }$
and
![]() $q_{(f\upharpoonright \alpha ) ^\smallfrown \xi }$
force contradictory information about
$q_{(f\upharpoonright \alpha ) ^\smallfrown \xi }$
force contradictory information about
![]() $\dot {d}\cap x_{f\upharpoonright \alpha } \subseteq \dot {d}\cap x$
. Since f extends
$\dot {d}\cap x_{f\upharpoonright \alpha } \subseteq \dot {d}\cap x$
. Since f extends
![]() $(f\upharpoonright \alpha ) ^\smallfrown \zeta $
and g extends
$(f\upharpoonright \alpha ) ^\smallfrown \zeta $
and g extends
![]() $(f\upharpoonright n) ^\smallfrown \xi $
, it follows that
$(f\upharpoonright n) ^\smallfrown \xi $
, it follows that
![]() $q_f$
and
$q_f$
and
![]() $q_g$
disagree on
$q_g$
disagree on
![]() $\dot {d} \cap x$
.
$\dot {d} \cap x$
.
We conclude that each
![]() $f \in \nu ^\tau $
forces a distinct value for
$f \in \nu ^\tau $
forces a distinct value for
![]() $\dot {d}\cap x$
, so there must be at least
$\dot {d}\cap x$
, so there must be at least
![]() $\nu ^\tau> \nu $
potential values for
$\nu ^\tau> \nu $
potential values for
![]() $\dot {d}\cap x$
. But since
$\dot {d}\cap x$
. But since
![]() $\dot {d}$
is thinly
$\dot {d}$
is thinly
![]() $\nu ^+$
-approximated, there are at most
$\nu ^+$
-approximated, there are at most
![]() $\nu $
potential values for
$\nu $
potential values for
![]() $\dot {d}$
and thus for
$\dot {d}$
and thus for
![]() $\dot {d}\cap x$
. This is a contradiction.
$\dot {d}\cap x$
. This is a contradiction.
To obtain the strong tree property and ITP at successors of singular cardinals, as in [Reference Neeman14] and [Reference Hachtman and Sinapova8] we will use the concept of systems of branches.
Definition 2.21. Let
![]() $D \subseteq \operatorname {\mathrm {Ord}}, \rho \in \operatorname {\mathrm {Ord}}$
, and I be an index set. A system on
$D \subseteq \operatorname {\mathrm {Ord}}, \rho \in \operatorname {\mathrm {Ord}}$
, and I be an index set. A system on
![]() $D \times \rho $
is a family
$D \times \rho $
is a family
![]() $\langle R_s \rangle _{s\in I}$
of transitive, reflexive relations on
$\langle R_s \rangle _{s\in I}$
of transitive, reflexive relations on
![]() $D \times \rho $
such that:
$D \times \rho $
such that:
-
(1) If
 $(\alpha , \xi ) R_s (\beta , \zeta )$
and
$(\alpha , \xi ) R_s (\beta , \zeta )$
and
 $(\alpha , \xi ) \neq (\beta , \zeta )$
, then
$(\alpha , \xi ) \neq (\beta , \zeta )$
, then
 $\alpha < \beta $
.
$\alpha < \beta $
. -
(2) If
 $(\alpha _0, \xi _0)$
and
$(\alpha _0, \xi _0)$
and
 $(\alpha _1, \xi _1)$
are both
$(\alpha _1, \xi _1)$
are both
 $R_s$
-below
$R_s$
-below
 $(\beta , \zeta )$
, then
$(\beta , \zeta )$
, then
 $(\alpha _0, \xi _0)$
and
$(\alpha _0, \xi _0)$
and
 $(\alpha _1, \xi _1)$
are comparable in
$(\alpha _1, \xi _1)$
are comparable in
 $R_s$
.
$R_s$
. -
(3) For every
 $\alpha < \beta $
both in D, there are
$\alpha < \beta $
both in D, there are
 $s\in I$
and
$s\in I$
and
 $\xi , \zeta \in \rho $
so that
$\xi , \zeta \in \rho $
so that
 $(\alpha , \xi ) R_s (\beta , \zeta )$
.
$(\alpha , \xi ) R_s (\beta , \zeta )$
.
A branch through
![]() $R_s$
is a subset of
$R_s$
is a subset of
![]() $D\times \rho $
that is linearly ordered by
$D\times \rho $
that is linearly ordered by
![]() $R_s$
and downwards
$R_s$
and downwards
![]() $R_s$
-closed. Note that each branch can be viewed as a partial function
$R_s$
-closed. Note that each branch can be viewed as a partial function
![]() $b:D\rightharpoonup \rho $
. A branch through
$b:D\rightharpoonup \rho $
. A branch through
![]() $R_s$
is cofinal if its domain is cofinal in D. A system of branches through
$R_s$
is cofinal if its domain is cofinal in D. A system of branches through
![]() $\langle R_s\rangle _{s\in I}$
is a family
$\langle R_s\rangle _{s\in I}$
is a family
![]() $\langle b_\eta \rangle _{\eta \in J}$
so that each
$\langle b_\eta \rangle _{\eta \in J}$
so that each
![]() $b_\eta $
is a branch through some
$b_\eta $
is a branch through some
![]() $R_{s(\eta )}$
, and
$R_{s(\eta )}$
, and
![]() $D = \bigcup _{\eta \in J} \operatorname {\mathrm {dom}}(b_\eta )$
.
$D = \bigcup _{\eta \in J} \operatorname {\mathrm {dom}}(b_\eta )$
.
We have the following branch lemma for systems of branches. This lemma was originally stated for a singular cardinal
![]() $\nu $
of countable cofinality, but the same proof applies for any cofinality.
$\nu $
of countable cofinality, but the same proof applies for any cofinality.
Lemma 2.22 [Reference Neeman14, Lemma 3.3 and Remark 3.4].
Let
![]() $\nu $
be a strong limit singular cardinal, and let
$\nu $
be a strong limit singular cardinal, and let
![]() $\langle R_s\rangle _{s\in I}$
be a system in V on
$\langle R_s\rangle _{s\in I}$
be a system in V on
![]() $D\times \rho $
, with D cofinal in
$D\times \rho $
, with D cofinal in
![]() $\nu ^+$
. Let
$\nu ^+$
. Let
![]() $\mathbb {P}$
be a poset in V, and let
$\mathbb {P}$
be a poset in V, and let
![]() $\kappa < \nu $
be a regular cardinal above
$\kappa < \nu $
be a regular cardinal above
![]() $\max (|I|, \rho )^+$
, so that
$\max (|I|, \rho )^+$
, so that
![]() $:$
$:$
-
(1) The empty condition in
 $\mathbb {P}$
forces that there exists a system
$\mathbb {P}$
forces that there exists a system
 $\langle b_\eta \rangle _{\eta \in J}$
of branches through
$\langle b_\eta \rangle _{\eta \in J}$
of branches through
 $\langle R_s \rangle _{s\in I}$
, with
$\langle R_s \rangle _{s\in I}$
, with
 $|J|^+ < \kappa $
.
$|J|^+ < \kappa $
. -
(2) For
 $\lambda = \max (|I|,|J|,\rho )^+ < \kappa $
, there is a poset
$\lambda = \max (|I|,|J|,\rho )^+ < \kappa $
, there is a poset
 $\mathbb {P}^\lambda $
adding
$\mathbb {P}^\lambda $
adding
 $\lambda $
mutually generic filters for
$\lambda $
mutually generic filters for
 $\mathbb {P}$
such that
$\mathbb {P}$
such that
 $\mathbb {P}^\lambda $
is
$\mathbb {P}^\lambda $
is
 $<\kappa $
-distributive.
$<\kappa $
-distributive.
Then there exists
![]() $\eta $
so that
$\eta $
so that
![]() $b_\eta $
is cofinal and belongs to V. In particular, there is
$b_\eta $
is cofinal and belongs to V. In particular, there is
![]() $s \in I$
so that in V,
$s \in I$
so that in V,
![]() $R_s$
has a cofinal branch.
$R_s$
has a cofinal branch.
3. ITP below
 $\aleph _{\omega +1}$
with the strong tree property at
$\aleph _{\omega +1}$
with the strong tree property at
 $\aleph _{\omega +1}$
$\aleph _{\omega +1}$
Using the techniques from the previous section, we show that in the model of [Reference Neeman14],
![]() $\operatorname {\mathrm {ITP}}$
holds at
$\operatorname {\mathrm {ITP}}$
holds at
![]() $\aleph _n$
for all
$\aleph _n$
for all
![]() $2 \leq n < \omega $
, and the strong tree property holds at
$2 \leq n < \omega $
, and the strong tree property holds at
![]() $\aleph _{\omega +1}$
.
$\aleph _{\omega +1}$
.
3.1. The forcing
First we recall Neeman’s construction. See [Reference Neeman14] for a more detailed exposition. (In this paper we adopt the convention that a
![]() $\kappa $
-closed forcing is a forcing where every sequence of length less than
$\kappa $
-closed forcing is a forcing where every sequence of length less than
![]() $\kappa $
has a lower bound; [Reference Neeman14] uses a different convention that includes sequences of length
$\kappa $
has a lower bound; [Reference Neeman14] uses a different convention that includes sequences of length
![]() $\kappa $
. So in particular, we will refer to
$\kappa $
. So in particular, we will refer to
![]() $\mu ^+$
-closed forcings where [Reference Neeman14] refers to
$\mu ^+$
-closed forcings where [Reference Neeman14] refers to
![]() $\mu $
-closed forcings.)
$\mu $
-closed forcings.)
Let
![]() $\langle \kappa _n \mid 2 \leq n < \omega \rangle $
be an increasing sequence of indestructibly supercompact cardinals with supremum
$\langle \kappa _n \mid 2 \leq n < \omega \rangle $
be an increasing sequence of indestructibly supercompact cardinals with supremum
![]() $\nu $
, and suppose there is a partial function
$\nu $
, and suppose there is a partial function
![]() $\phi $
such that for all
$\phi $
such that for all
![]() $2<n<\omega $
,
$2<n<\omega $
,
![]() $\phi \upharpoonright \kappa _n$
is an indestructible Laver function for
$\phi \upharpoonright \kappa _n$
is an indestructible Laver function for
![]() $\kappa _n$
. That is, for each
$\kappa _n$
. That is, for each
![]() $A \in V$
,
$A \in V$
,
![]() $\gamma \in \operatorname {\mathrm {Ord}}$
, and every extension
$\gamma \in \operatorname {\mathrm {Ord}}$
, and every extension
![]() $V[E]$
of V by a
$V[E]$
of V by a
![]() $<\kappa _n$
-directed closed forcing, there is a
$<\kappa _n$
-directed closed forcing, there is a
![]() $\gamma $
-supercompactness embedding
$\gamma $
-supercompactness embedding
![]() $\pi $
in
$\pi $
in
![]() $V[E]$
with critical point
$V[E]$
with critical point
![]() $\kappa _n$
, such that
$\kappa _n$
, such that
![]() $\pi \upharpoonright \operatorname {\mathrm {Ord}} \in V$
,
$\pi \upharpoonright \operatorname {\mathrm {Ord}} \in V$
,
![]() $\pi (\phi )(\kappa _n)=A$
, and the next point in
$\pi (\phi )(\kappa _n)=A$
, and the next point in
![]() $\operatorname {\mathrm {dom}}(\pi (\phi ))$
above
$\operatorname {\mathrm {dom}}(\pi (\phi ))$
above
![]() $\kappa _n$
is greater than
$\kappa _n$
is greater than
![]() $\gamma $
. Such a function can be arranged via the standard construction for Laver indestructibility (see [Reference Neeman14, Section 4] for details). By restricting the domain if necessary, we can assume that for all
$\gamma $
. Such a function can be arranged via the standard construction for Laver indestructibility (see [Reference Neeman14, Section 4] for details). By restricting the domain if necessary, we can assume that for all
![]() $\alpha \in \operatorname {\mathrm {dom}}(\phi )$
, if
$\alpha \in \operatorname {\mathrm {dom}}(\phi )$
, if
![]() $\gamma $
is in
$\gamma $
is in
![]() $\operatorname {\mathrm {dom}}(\phi )\cap \alpha $
then
$\operatorname {\mathrm {dom}}(\phi )\cap \alpha $
then
![]() $\phi (\gamma ) \in V_\alpha $
.
$\phi (\gamma ) \in V_\alpha $
.
The forcing consists of three parts: Cohen forcings to ensure that
![]() $2^{\kappa _n} = \kappa _{n+2}$
for each
$2^{\kappa _n} = \kappa _{n+2}$
for each
![]() $n \geq 2$
, Laver preparation to ensure that each
$n \geq 2$
, Laver preparation to ensure that each
![]() $\kappa _n$
is indestructibly generically supercompact, and Mitchell-style collapses to make each
$\kappa _n$
is indestructibly generically supercompact, and Mitchell-style collapses to make each
![]() $\kappa _n$
become
$\kappa _n$
become
![]() $\aleph _n$
. The situation is somewhat complicated by the fact that in order to obtain ITP (or even just the tree property) at
$\aleph _n$
. The situation is somewhat complicated by the fact that in order to obtain ITP (or even just the tree property) at
![]() $\aleph _{\omega +1}$
later on, we cannot fix the cardinal that will become
$\aleph _{\omega +1}$
later on, we cannot fix the cardinal that will become
![]() $\aleph _1$
in advance. As in [Reference Neeman14], we define a set Index that gives us the possibilities for the new
$\aleph _1$
in advance. As in [Reference Neeman14], we define a set Index that gives us the possibilities for the new
![]() $\aleph _1$
, and define our poset using a lottery sum over the elements of Index.
$\aleph _1$
, and define our poset using a lottery sum over the elements of Index.
First we define the Cohen piece of the forcing.
Definition 3.1. For
![]() $n \geq 2$
, let
$n \geq 2$
, let
![]() $\mathbb {A}_n \mathrel {\mathop :}= \operatorname {\mathrm {Add}}(\kappa _n, \kappa _{n+2})$
. Let
$\mathbb {A}_n \mathrel {\mathop :}= \operatorname {\mathrm {Add}}(\kappa _n, \kappa _{n+2})$
. Let
![]() $\kappa _0$
denote
$\kappa _0$
denote
![]() $\omega $
, and set
$\omega $
, and set
![]() $\mathbb {A}_0 \mathrel {\mathop :}= \operatorname {\mathrm {Add}}(\omega , \kappa _2)$
. Let
$\mathbb {A}_0 \mathrel {\mathop :}= \operatorname {\mathrm {Add}}(\omega , \kappa _2)$
. Let
![]() $\mathbb {A}_1 = \sum _{\mu \in \text {Index}} \operatorname {\mathrm {Add}}(\mu ^+, \kappa _3)$
. (The set Index will be defined below, as it relies on the initial stage of both the Cohen and Laver parts of the forcing.) We use
$\mathbb {A}_1 = \sum _{\mu \in \text {Index}} \operatorname {\mathrm {Add}}(\mu ^+, \kappa _3)$
. (The set Index will be defined below, as it relies on the initial stage of both the Cohen and Laver parts of the forcing.) We use
![]() $\kappa _1$
to refer to the value of
$\kappa _1$
to refer to the value of
![]() $\mu ^+$
chosen by a fixed generic. Let
$\mu ^+$
chosen by a fixed generic. Let
![]() $\mathbb {A}$
be the full support product of
$\mathbb {A}$
be the full support product of
![]() $\mathbb {A}_n$
for
$\mathbb {A}_n$
for
![]() $n < \omega $
.
$n < \omega $
.
We will use
![]() $A_{[n,m]}$
to denote
$A_{[n,m]}$
to denote
![]() $\prod _{n\leq i\leq m}A_i$
; half-open and open intervals are defined similarly.
$\prod _{n\leq i\leq m}A_i$
; half-open and open intervals are defined similarly.
![]() $\mathbb {A}\upharpoonright \alpha $
denotes
$\mathbb {A}\upharpoonright \alpha $
denotes
![]() $\mathbb {A}_{[0,n)}\times \mathbb {A}_n\upharpoonright \alpha $
, where n is the least such that
$\mathbb {A}_{[0,n)}\times \mathbb {A}_n\upharpoonright \alpha $
, where n is the least such that
![]() $\alpha \leq \kappa _{n+2}$
.
$\alpha \leq \kappa _{n+2}$
.
Next we define the Laver preparation.
Definition 3.2. We define two posets,
![]() $\mathbb {B}$
in V and
$\mathbb {B}$
in V and
![]() $\mathbb {U}$
in the extension of V by
$\mathbb {U}$
in the extension of V by
![]() $\mathbb {A}$
, recursively as follows:
$\mathbb {A}$
, recursively as follows:
-
(1) Conditions p in
 $\mathbb {B}$
are functions with
$\mathbb {B}$
are functions with
 $\operatorname {\mathrm {dom}}(p) \subseteq \nu $
so that for every inaccessible cardinal
$\operatorname {\mathrm {dom}}(p) \subseteq \nu $
so that for every inaccessible cardinal
 $\alpha $
,
$\alpha $
,
 $|\operatorname {\mathrm {dom}}(p)\cap \alpha | < \alpha $
. In particular,
$|\operatorname {\mathrm {dom}}(p)\cap \alpha | < \alpha $
. In particular,
 $|\operatorname {\mathrm {dom}}(p)\cap \kappa _{n+2}| < \kappa _{n+2}$
for each n.
$|\operatorname {\mathrm {dom}}(p)\cap \kappa _{n+2}| < \kappa _{n+2}$
for each n. -
(2) If
 $\alpha \in \operatorname {\mathrm {dom}}(p)$
, then
$\alpha \in \operatorname {\mathrm {dom}}(p)$
, then
 $\alpha $
is inaccessible, not equal to any
$\alpha $
is inaccessible, not equal to any
 $\kappa _n$
,
$\kappa _n$
,
 $\alpha \in \operatorname {\mathrm {dom}}(\phi )$
, and
$\alpha \in \operatorname {\mathrm {dom}}(\phi )$
, and
 $\phi (\alpha )$
is an
$\phi (\alpha )$
is an
 $(\mathbb {A}\upharpoonright \alpha )\ast (\dot {\mathbb {U}}\upharpoonright \alpha )$
name for a poset forced to be
$(\mathbb {A}\upharpoonright \alpha )\ast (\dot {\mathbb {U}}\upharpoonright \alpha )$
name for a poset forced to be
 $<\alpha $
-directed closed.
$<\alpha $
-directed closed. -
(3)
 $p(\alpha )$
is an
$p(\alpha )$
is an
 $(\mathbb {A}\upharpoonright \alpha ) \ast (\dot {\mathbb {U}}\upharpoonright \alpha )$
name for a condition in
$(\mathbb {A}\upharpoonright \alpha ) \ast (\dot {\mathbb {U}}\upharpoonright \alpha )$
name for a condition in
 $\phi (\alpha )$
.
$\phi (\alpha )$
. -
(4)
 $p^* \leq p$
in
$p^* \leq p$
in
 $\mathbb {B}$
if and only if
$\mathbb {B}$
if and only if
 $\operatorname {\mathrm {dom}}(p^*)\supseteq \operatorname {\mathrm {dom}}(p)$
and for each
$\operatorname {\mathrm {dom}}(p^*)\supseteq \operatorname {\mathrm {dom}}(p)$
and for each
 $\alpha \in \operatorname {\mathrm {dom}}(p)$
,
$\alpha \in \operatorname {\mathrm {dom}}(p)$
,
 $(\emptyset , p^*\upharpoonright \alpha )$
forces in
$(\emptyset , p^*\upharpoonright \alpha )$
forces in
 $(\mathbb {A}\upharpoonright \alpha ) \ast (\dot {\mathbb {U}}\upharpoonright \alpha )$
that
$(\mathbb {A}\upharpoonright \alpha ) \ast (\dot {\mathbb {U}}\upharpoonright \alpha )$
that
 $p^*(\alpha ) \leq p(\alpha )$
.
$p^*(\alpha ) \leq p(\alpha )$
. -
(5) Let A be generic for
 $\mathbb {A}$
.
$\mathbb {A}$
.
 $\mathbb {U} = \dot {\mathbb {U}}[A]$
has the same conditions as
$\mathbb {U} = \dot {\mathbb {U}}[A]$
has the same conditions as
 $\mathbb {B}$
. The order is given by
$\mathbb {B}$
. The order is given by
 $p^* \leq p$
if and only if
$p^* \leq p$
if and only if
 $\operatorname {\mathrm {dom}}(p^*) \supseteq \operatorname {\mathrm {dom}}(p)$
and there exists a condition
$\operatorname {\mathrm {dom}}(p^*) \supseteq \operatorname {\mathrm {dom}}(p)$
and there exists a condition
 $a^*$
in A so that for every
$a^*$
in A so that for every
 $\alpha \in \operatorname {\mathrm {dom}}(p)$
,
$\alpha \in \operatorname {\mathrm {dom}}(p)$
,
 $(a^*\upharpoonright \alpha , p^*\upharpoonright \alpha )$
forces in
$(a^*\upharpoonright \alpha , p^*\upharpoonright \alpha )$
forces in
 $(\mathbb {A}\upharpoonright \alpha ) \ast (\dot {\mathbb {U}}\upharpoonright \alpha )$
that
$(\mathbb {A}\upharpoonright \alpha ) \ast (\dot {\mathbb {U}}\upharpoonright \alpha )$
that
 $p^*(\alpha ) \leq p(\alpha )$
.
$p^*(\alpha ) \leq p(\alpha )$
.
Let
![]() $\mathbb {U}_0 = U\upharpoonright \kappa _2$
, and for all
$\mathbb {U}_0 = U\upharpoonright \kappa _2$
, and for all
![]() $n> 0$
let
$n> 0$
let
![]() $\mathbb {U}_n = \mathbb {U}\upharpoonright [\kappa _{n+1}, \kappa _{n+2})$
. We define
$\mathbb {U}_n = \mathbb {U}\upharpoonright [\kappa _{n+1}, \kappa _{n+2})$
. We define
![]() $\mathbb {U}_{[0,n]} = \mathbb {U}\upharpoonright \kappa _{n+2}$
; note that
$\mathbb {U}_{[0,n]} = \mathbb {U}\upharpoonright \kappa _{n+2}$
; note that
![]() $\mathbb {U}_{[0,n]}$
is a poset in
$\mathbb {U}_{[0,n]}$
is a poset in
![]() $V[A_{[0,n]}]$
.
$V[A_{[0,n]}]$
.
Definition 3.3. Let
![]() $\beta < \nu $
and let F be a filter in
$\beta < \nu $
and let F be a filter in
![]() $\mathbb {A}\ast \dot {\mathbb {U}}\upharpoonright \beta $
. We define
$\mathbb {A}\ast \dot {\mathbb {U}}\upharpoonright \beta $
. We define
![]() $\mathbb {B}^{+F}\upharpoonright [\beta , \nu )$
to consist of conditions
$\mathbb {B}^{+F}\upharpoonright [\beta , \nu )$
to consist of conditions
![]() $p\in \mathbb {B}$
with
$p\in \mathbb {B}$
with
![]() $\operatorname {\mathrm {dom}}(p) \subseteq [\beta , \nu )$
with the ordering
$\operatorname {\mathrm {dom}}(p) \subseteq [\beta , \nu )$
with the ordering
![]() $p^* \leq p$
if and only if
$p^* \leq p$
if and only if
![]() $\operatorname {\mathrm {dom}}(p^*) \supseteq \operatorname {\mathrm {dom}}(p)$
and there exists
$\operatorname {\mathrm {dom}}(p^*) \supseteq \operatorname {\mathrm {dom}}(p)$
and there exists
![]() $(a,b) \in F$
so that for every
$(a,b) \in F$
so that for every
![]() $\alpha \in \operatorname {\mathrm {dom}}(p)$
,
$\alpha \in \operatorname {\mathrm {dom}}(p)$
,
![]() $(a\upharpoonright \alpha , b\cup p^*\upharpoonright \alpha )$
forces
$(a\upharpoonright \alpha , b\cup p^*\upharpoonright \alpha )$
forces
![]() $p^*(\alpha ) \leq p(\alpha )$
.
$p^*(\alpha ) \leq p(\alpha )$
.
Remark 3.4. Given a generic
![]() $A \ast U$
for
$A \ast U$
for
![]() $\mathbb {A} \ast \dot {\mathbb {U}}$
over V, with
$\mathbb {A} \ast \dot {\mathbb {U}}$
over V, with
![]() $F = A\upharpoonright \beta \ast U\upharpoonright \beta $
,
$F = A\upharpoonright \beta \ast U\upharpoonright \beta $
,
![]() $U \upharpoonright [\beta ,\nu )$
may not be a generic filter for
$U \upharpoonright [\beta ,\nu )$
may not be a generic filter for
![]() $\mathbb {B}^{+F} \upharpoonright [\beta ,\nu )$
. However, we can force to add a filter
$\mathbb {B}^{+F} \upharpoonright [\beta ,\nu )$
. However, we can force to add a filter
![]() $G \subseteq U\upharpoonright [\beta ,\nu ) $
that is generic for
$G \subseteq U\upharpoonright [\beta ,\nu ) $
that is generic for
![]() $\mathbb {B}^{+F}\upharpoonright [\beta ,\nu )$
. We call this forcing the factor forcing refining
$\mathbb {B}^{+F}\upharpoonright [\beta ,\nu )$
. We call this forcing the factor forcing refining
![]() $U\upharpoonright \beta $
to a generic for
$U\upharpoonright \beta $
to a generic for
![]() $\mathbb {B}^{+F}\upharpoonright [\beta ,\nu )$
.
$\mathbb {B}^{+F}\upharpoonright [\beta ,\nu )$
.
Fact 3.5 [Reference Neeman14, Claim 4.7].
Let
![]() $\bar {\beta } \leq \beta $
. Suppose that
$\bar {\beta } \leq \beta $
. Suppose that
![]() $\bar {F}$
is generic for
$\bar {F}$
is generic for
![]() $\mathbb {A}\upharpoonright \bar {\beta }\ast \dot {\mathbb {U}}\upharpoonright \bar {\beta }$
over V. Then
$\mathbb {A}\upharpoonright \bar {\beta }\ast \dot {\mathbb {U}}\upharpoonright \bar {\beta }$
over V. Then
![]() $\mathbb {B}^{+\bar {F}}\upharpoonright [\beta ,\nu )$
is
$\mathbb {B}^{+\bar {F}}\upharpoonright [\beta ,\nu )$
is
![]() $<\beta $
directed closed in
$<\beta $
directed closed in
![]() $V[\bar {F}]$
.
$V[\bar {F}]$
.
Fact 3.6 [Reference Neeman14, Lemma 4.12].
Let
![]() $n < \omega $
and let
$n < \omega $
and let
![]() $A\ast U_{[0,n]}$
be generic for
$A\ast U_{[0,n]}$
be generic for
![]() $\mathbb {A}\ast \dot {\mathbb {U}}_{[0,n]}$
over V. Then in
$\mathbb {A}\ast \dot {\mathbb {U}}_{[0,n]}$
over V. Then in
![]() $V[A][U_{[0,n]}]$
,
$V[A][U_{[0,n]}]$
,
![]() $\kappa _{n+2}$
is generically supercompact. Moreover, this supercompactness is indestructible under forcing with
$\kappa _{n+2}$
is generically supercompact. Moreover, this supercompactness is indestructible under forcing with
![]() $<\kappa _{n+2}$
-directed-closed forcings in
$<\kappa _{n+2}$
-directed-closed forcings in
![]() $V[A_{[0,n]}][U_{[0,n]}]$
. The forcing poset producing this embedding is
$V[A_{[0,n]}][U_{[0,n]}]$
. The forcing poset producing this embedding is
![]() $\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V\times \operatorname {\mathrm {Add}}(\kappa _{n+1}, \pi (\kappa _{n+3}))^V$
.
$\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V\times \operatorname {\mathrm {Add}}(\kappa _{n+1}, \pi (\kappa _{n+3}))^V$
.
By this we mean the following. Let
![]() $\hat {A}$
be generic for
$\hat {A}$
be generic for
![]() $\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V\times \operatorname {\mathrm {Add}}(\kappa _{n+1}, \pi (\kappa _{n+3}))^V$
. Let
$\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V\times \operatorname {\mathrm {Add}}(\kappa _{n+1}, \pi (\kappa _{n+3}))^V$
. Let
![]() $\lambda \geq \kappa _{n+2}$
, and let G be generic for some
$\lambda \geq \kappa _{n+2}$
, and let G be generic for some
![]() $\kappa _{n+2}$
-directed-closed forcing in
$\kappa _{n+2}$
-directed-closed forcing in
![]() $V[A_{[0,n]}][U_{[0,n]}]$
. Then in the generic extension
$V[A_{[0,n]}][U_{[0,n]}]$
. Then in the generic extension
![]() $V[A][U_{[0,n]}][G][\hat {A}]$
there is an elementary embedding
$V[A][U_{[0,n]}][G][\hat {A}]$
there is an elementary embedding
![]() $\pi : V[A][U_{[0,n]}][G] \to V^*[A^*][U^*_{[0,n]}][G^*]$
with critical point
$\pi : V[A][U_{[0,n]}][G] \to V^*[A^*][U^*_{[0,n]}][G^*]$
with critical point
![]() $\kappa _{n+2}$
, such that
$\kappa _{n+2}$
, such that
![]() $\pi (\kappa _{n+2})> \lambda $
,
$\pi (\kappa _{n+2})> \lambda $
,
![]() $\pi \upharpoonright \operatorname {\mathrm {Ord}} \in V$
, and
$\pi \upharpoonright \operatorname {\mathrm {Ord}} \in V$
, and
![]() $V^*[A^*][U^*_{[0,n]}][G^*]$
is closed under
$V^*[A^*][U^*_{[0,n]}][G^*]$
is closed under
![]() $\lambda $
-sequences in this generic extension.
$\lambda $
-sequences in this generic extension.
Definition 3.7. We define the set Index as the set of all
![]() $\mu < \kappa _2$
so that:
$\mu < \kappa _2$
so that:
-
(1)
 $\mu $
is a strong limit cardinal of cofinality
$\mu $
is a strong limit cardinal of cofinality
 $\omega $
and
$\omega $
and
 $\operatorname {\mathrm {dom}}(\phi )$
has a largest point
$\operatorname {\mathrm {dom}}(\phi )$
has a largest point
 $\lambda $
below
$\lambda $
below
 $\mu $
.
$\mu $
. -
(2) Over any extension
 $V[E]$
of V by a
$V[E]$
of V by a
 $\mu ^+$
closed poset, the further extension by
$\mu ^+$
closed poset, the further extension by
 $\mathbb {A}_0\upharpoonright \lambda \ast \dot {U}_0\upharpoonright \lambda + 1$
does not collapse
$\mathbb {A}_0\upharpoonright \lambda \ast \dot {U}_0\upharpoonright \lambda + 1$
does not collapse
 $(\mu ^+)^V$
.
$(\mu ^+)^V$
. -
(3)
 $\mathbb {A}_0 \upharpoonright \lambda \ast \dot {U}_0\upharpoonright \lambda +1$
has size at most
$\mathbb {A}_0 \upharpoonright \lambda \ast \dot {U}_0\upharpoonright \lambda +1$
has size at most
 $\mu ^+$
.
$\mu ^+$
.
We note that there are many elements in
![]() $\operatorname {\mathrm {Index}}$
. In particular, consider the case where
$\operatorname {\mathrm {Index}}$
. In particular, consider the case where
![]() $\gamma $
is a strong limit cardinal with cofinality
$\gamma $
is a strong limit cardinal with cofinality
![]() $\omega $
above
$\omega $
above
![]() $\kappa _2$
and
$\kappa _2$
and
![]() $i:V \to V^*$
is some
$i:V \to V^*$
is some
![]() $\gamma $
-supercompactness embedding with critical point
$\gamma $
-supercompactness embedding with critical point
![]() $\kappa _2$
. Then the largest point of
$\kappa _2$
. Then the largest point of
![]() $\operatorname {\mathrm {dom}}(i(\phi ))$
below
$\operatorname {\mathrm {dom}}(i(\phi ))$
below
![]() $\gamma $
will be
$\gamma $
will be
![]() $\kappa _2$
; by elementarity there are many
$\kappa _2$
; by elementarity there are many
![]() $\mu $
satisfying the first condition. If
$\mu $
satisfying the first condition. If
![]() $|\phi (\lambda )| < \mu $
, then the second and third conditions will be satisfied, since
$|\phi (\lambda )| < \mu $
, then the second and third conditions will be satisfied, since
![]() $\mathbb {A}_0\upharpoonright \lambda \ast \dot {U}\upharpoonright \lambda +1$
will have size less than
$\mathbb {A}_0\upharpoonright \lambda \ast \dot {U}\upharpoonright \lambda +1$
will have size less than
![]() $\mu $
and so will not be able to collapse
$\mu $
and so will not be able to collapse
![]() $\mu ^+.$
$\mu ^+.$
Finally, we define the collapses.
Definition 3.8. For each
![]() $n < \omega $
, define
$n < \omega $
, define
![]() $\mathbb {C}_n$
in V as follows. Conditions in
$\mathbb {C}_n$
in V as follows. Conditions in
![]() $\mathbb {C}_n$
are functions p such that:
$\mathbb {C}_n$
are functions p such that:
-
(1)
 $\operatorname {\mathrm {dom}}(p)$
is contained in the interval
$\operatorname {\mathrm {dom}}(p)$
is contained in the interval
 $(\kappa _{n+1}, \kappa _{n+2})$
and
$(\kappa _{n+1}, \kappa _{n+2})$
and
 $|\operatorname {\mathrm {dom}}(p)| < \kappa _{n+1}$
.
$|\operatorname {\mathrm {dom}}(p)| < \kappa _{n+1}$
. -
(2) For each
 $\alpha \in \operatorname {\mathrm {dom}}(p)$
,
$\alpha \in \operatorname {\mathrm {dom}}(p)$
,
 $p(\alpha )$
is an
$p(\alpha )$
is an
 $(\mathbb {A}\upharpoonright \alpha )\ast (\dot {U}\upharpoonright \kappa _{n+1})$
name for a condition in the poset
$(\mathbb {A}\upharpoonright \alpha )\ast (\dot {U}\upharpoonright \kappa _{n+1})$
name for a condition in the poset
 $\operatorname {\mathrm {Add}}(\kappa _{n+1}, 1)$
of the extension by
$\operatorname {\mathrm {Add}}(\kappa _{n+1}, 1)$
of the extension by
 $(\mathbb {A}\upharpoonright \alpha )\ast (\dot {U}\upharpoonright \kappa _{n+1})$
.
$(\mathbb {A}\upharpoonright \alpha )\ast (\dot {U}\upharpoonright \kappa _{n+1})$
.
We define the ordering by
![]() $p^* \leq p$
if and only if
$p^* \leq p$
if and only if
![]() $\operatorname {\mathrm {dom}}(p^*) \supseteq \operatorname {\mathrm {dom}}(p)$
and for each
$\operatorname {\mathrm {dom}}(p^*) \supseteq \operatorname {\mathrm {dom}}(p)$
and for each
![]() $\alpha \in \operatorname {\mathrm {dom}}(p)$
, the empty condition in
$\alpha \in \operatorname {\mathrm {dom}}(p)$
, the empty condition in
![]() $(\mathbb {A}\upharpoonright \alpha )\ast (\dot {U}\upharpoonright \kappa _{n+1})$
forces that
$(\mathbb {A}\upharpoonright \alpha )\ast (\dot {U}\upharpoonright \kappa _{n+1})$
forces that
![]() $p^*(\alpha ) \leq p(\alpha )$
.
$p^*(\alpha ) \leq p(\alpha )$
.
Let
![]() $\mathbb {C}$
be the full support product of each
$\mathbb {C}$
be the full support product of each
![]() $\mathbb {C}_n$
.
$\mathbb {C}_n$
.
Note that
![]() $\mathbb {C}_0$
is defined using
$\mathbb {C}_0$
is defined using
![]() $\kappa _1$
, which is not a priori known. When we have access to a generic for
$\kappa _1$
, which is not a priori known. When we have access to a generic for
![]() $\mathbb {A}_1$
, we will use the
$\mathbb {A}_1$
, we will use the
![]() $\kappa _1$
determined by this generic; if not, we will view it as a parameter in the definition. We will occasionally refer to this poset as
$\kappa _1$
determined by this generic; if not, we will view it as a parameter in the definition. We will occasionally refer to this poset as
![]() $\mathbb {C}_0(\kappa _1)$
if the choice of
$\mathbb {C}_0(\kappa _1)$
if the choice of
![]() $\kappa _1$
is not clear from context.
$\kappa _1$
is not clear from context.
Definition 3.9. For a filter
![]() $F \subseteq \mathbb {A}\ast \dot {U}$
define the enrichment of
$F \subseteq \mathbb {A}\ast \dot {U}$
define the enrichment of
![]() $\mathbb {C}$
to F, denoted by
$\mathbb {C}$
to F, denoted by
![]() $\mathbb {C}^{+F}$
, to be the poset with the same conditions as
$\mathbb {C}^{+F}$
, to be the poset with the same conditions as
![]() $\mathbb {C}$
but the order given by
$\mathbb {C}$
but the order given by
![]() $p^* \leq p$
if and only if there exists a condition
$p^* \leq p$
if and only if there exists a condition
![]() $(a, u) \in F$
so that for each
$(a, u) \in F$
so that for each
![]() $\alpha \in \operatorname {\mathrm {dom}}(p)$
,
$\alpha \in \operatorname {\mathrm {dom}}(p)$
,
![]() $(a\upharpoonright \alpha , u\upharpoonright \kappa _i) \Vdash _{\mathbb {A}\upharpoonright \alpha \ast \dot {U}\upharpoonright \kappa _{i}} p^*(\alpha ) \leq p(\alpha )$
, where i is the largest such that
$(a\upharpoonright \alpha , u\upharpoonright \kappa _i) \Vdash _{\mathbb {A}\upharpoonright \alpha \ast \dot {U}\upharpoonright \kappa _{i}} p^*(\alpha ) \leq p(\alpha )$
, where i is the largest such that
![]() $\kappa _i \leq \alpha $
.
$\kappa _i \leq \alpha $
.
Remark 3.10. Let
![]() $A \ast U$
be generic for
$A \ast U$
be generic for
![]() $\mathbb {A}\ast \mathbb {U}$
,
$\mathbb {A}\ast \mathbb {U}$
,
![]() $F = A\upharpoonright \kappa _n \ast U\upharpoonright \kappa _n$
, and let S be generic for
$F = A\upharpoonright \kappa _n \ast U\upharpoonright \kappa _n$
, and let S be generic for
![]() $\mathbb {C}^{+A\ast U}$
. As before, we can find a factor forcing refining
$\mathbb {C}^{+A\ast U}$
. As before, we can find a factor forcing refining
![]() $S\upharpoonright [\kappa _n, \nu )$
to a generic for
$S\upharpoonright [\kappa _n, \nu )$
to a generic for
![]() $\mathbb {C}^{+F}\upharpoonright [\kappa _n, \nu )$
.
$\mathbb {C}^{+F}\upharpoonright [\kappa _n, \nu )$
.
Fact 3.11 [Reference Neeman14, Claim 4.15].
-
(1) Let F be generic for
 $\mathbb {A}\upharpoonright \beta \ast \dot {\mathbb {U}}\upharpoonright \beta $
for
$\mathbb {A}\upharpoonright \beta \ast \dot {\mathbb {U}}\upharpoonright \beta $
for
 $\beta \leq \kappa _{n+1}$
. Then
$\beta \leq \kappa _{n+1}$
. Then
 $\mathbb {C}^{+F}\upharpoonright [\kappa _{n+1},\nu )$
is
$\mathbb {C}^{+F}\upharpoonright [\kappa _{n+1},\nu )$
is
 $<\kappa _{n+1}$
directed closed in
$<\kappa _{n+1}$
directed closed in
 $V[F]$
.
$V[F]$
. -
(2) Let
 $\beta \in (\kappa _{n+1}, \kappa _{n+2})$
and let F be generic for
$\beta \in (\kappa _{n+1}, \kappa _{n+2})$
and let F be generic for
 $\mathbb {A}\upharpoonright \beta \ast \dot {U}\upharpoonright \kappa _{n+1}.$
Then
$\mathbb {A}\upharpoonright \beta \ast \dot {U}\upharpoonright \kappa _{n+1}.$
Then
 $\mathbb {C}^{+F}\upharpoonright [\beta ,\kappa _{n+2})$
is
$\mathbb {C}^{+F}\upharpoonright [\beta ,\kappa _{n+2})$
is
 $<\kappa _{n+1}$
directed closed in
$<\kappa _{n+1}$
directed closed in
 $V[F]$
.
$V[F]$
.
Let A be generic for
![]() $\mathbb {A}$
, U be generic for
$\mathbb {A}$
, U be generic for
![]() $\mathbb {U}$
over
$\mathbb {U}$
over
![]() $V[A]$
, S be generic for
$V[A]$
, S be generic for
![]() $\mathbb {C}^{+A\ast U}$
over
$\mathbb {C}^{+A\ast U}$
over
![]() $V[A][U]$
, and e be generic for
$V[A][U]$
, and e be generic for
![]() $\operatorname {\mathrm {Col}}(\omega , \mu )$
over
$\operatorname {\mathrm {Col}}(\omega , \mu )$
over
![]() $V[A][U][S]$
, noting that
$V[A][U][S]$
, noting that
![]() $\mu $
is determined by the generic for
$\mu $
is determined by the generic for
![]() $\mathbb {A}_1$
included in A. The final model is
$\mathbb {A}_1$
included in A. The final model is
![]() $V[A][U][S][e]$
.
$V[A][U][S][e]$
.
The cardinal structure in this model is what one would expect.
Fact 3.12. In
![]() $V[A][U][S][e]$
, the following properties hold.
$V[A][U][S][e]$
, the following properties hold.
-
•
 $\kappa _n = \aleph _n$
for each n.
$\kappa _n = \aleph _n$
for each n. -
•
 $2^{\kappa _n} = \kappa _{n+2}$
for each n.
$2^{\kappa _n} = \kappa _{n+2}$
for each n. -
•
 $2^\omega = \kappa _2$
.
$2^\omega = \kappa _2$
.
Fact 3.13 [Reference Neeman14, Lemma 4.24].
V has the
![]() $<\kappa _n$
-covering property with respect to
$<\kappa _n$
-covering property with respect to
![]() $V[A][U][S][e]$
for all
$V[A][U][S][e]$
for all
![]() $n \geq 2$
.
$n \geq 2$
.
3.2. The strong tree property at the successor of a singular
To obtain the strong tree property at
![]() $\aleph _{\omega +1}$
, we will generalize [Reference Neeman14, Lemma 3.10] to the strong tree property. For full generality, and to allow us to use it in later results, we will prove the lemma for the successor of a singular cardinal of any cofinality. The main obstacle here is that the strong tree property is a global property that must hold for every
$\aleph _{\omega +1}$
, we will generalize [Reference Neeman14, Lemma 3.10] to the strong tree property. For full generality, and to allow us to use it in later results, we will prove the lemma for the successor of a singular cardinal of any cofinality. The main obstacle here is that the strong tree property is a global property that must hold for every
![]() $\lambda $
; we solve this by bringing in an auxiliary poset that collapses
$\lambda $
; we solve this by bringing in an auxiliary poset that collapses
![]() $\lambda $
to
$\lambda $
to
![]() $\nu ^+$
.
$\nu ^+$
.
Theorem 3.14. Let
![]() $\tau $
be a regular cardinal. Let
$\tau $
be a regular cardinal. Let
![]() $\langle \kappa _{\rho } \mid \rho < \tau \rangle $
be a continuous sequence of regular cardinals above
$\langle \kappa _{\rho } \mid \rho < \tau \rangle $
be a continuous sequence of regular cardinals above
![]() $\tau $
, with supremum
$\tau $
, with supremum
![]() $\nu $
. Let
$\nu $
. Let
![]() $\operatorname {\mathrm {Index}} \subseteq \kappa _0$
, and fix
$\operatorname {\mathrm {Index}} \subseteq \kappa _0$
, and fix
![]() $\rho ' < \tau $
. For each
$\rho ' < \tau $
. For each
![]() $\mu \in \operatorname {\mathrm {Index}}$
, let
$\mu \in \operatorname {\mathrm {Index}}$
, let
![]() $\mathbb {L}_\mu $
be a forcing poset of size
$\mathbb {L}_\mu $
be a forcing poset of size
![]() $\leq \kappa _{\rho '}$
. Let R be a rank-initial segment of V satisfying a large enough fragment of ZFC. For all
$\leq \kappa _{\rho '}$
. Let R be a rank-initial segment of V satisfying a large enough fragment of ZFC. For all
![]() $\lambda \geq \nu ^+$
with
$\lambda \geq \nu ^+$
with
![]() $\lambda ^\nu = \lambda $
, let
$\lambda ^\nu = \lambda $
, let
![]() $\mathbb {K} = \mathbb {K}_\lambda $
be a poset preserving all cardinals
$\mathbb {K} = \mathbb {K}_\lambda $
be a poset preserving all cardinals
![]() $\leq \nu ^+$
that forces
$\leq \nu ^+$
that forces
![]() $|\lambda |=\nu ^+$
. Let K be generic for
$|\lambda |=\nu ^+$
. Let K be generic for
![]() $\mathbb {K}$
. Suppose that
$\mathbb {K}$
. Suppose that
![]() $:$
$:$
-
(1) For each
 $X \prec R$
with
$X \prec R$
with
 $|X| = \lambda $
and
$|X| = \lambda $
and
 $\lambda \subseteq X$
such that
$\lambda \subseteq X$
such that
 $\mathbb {K}$
is in the transitive part of X, let
$\mathbb {K}$
is in the transitive part of X, let
 $\bar {V} = \bar {V}_X$
be the transitive collapse of X. For stationarily many X, in
$\bar {V} = \bar {V}_X$
be the transitive collapse of X. For stationarily many X, in
 $V[K]$
there exists a
$V[K]$
there exists a
 $\nu ^+$
-Knaster poset
$\nu ^+$
-Knaster poset
 $\mathbb {H} = \mathbb {H}_X$
such that
$\mathbb {H} = \mathbb {H}_X$
such that
 $\mathbb {H}$
forces the existence of a generic
$\mathbb {H}$
forces the existence of a generic
 $\nu ^+$
-supercompactness embedding
$\nu ^+$
-supercompactness embedding
 $i: \bar {V}[K] \to \bar {M}[K^*]$
with critical point
$i: \bar {V}[K] \to \bar {M}[K^*]$
with critical point
 $\kappa _0$
such that
$\kappa _0$
such that
 $\nu \in i(\operatorname {\mathrm {Index}})$
, and a set L such that L is generic over
$\nu \in i(\operatorname {\mathrm {Index}})$
, and a set L such that L is generic over
 $\bar {M}[K^*]$
for
$\bar {M}[K^*]$
for
 $i(\mathbb {L})(\nu )$
.
$i(\mathbb {L})(\nu )$
. -
(2) In
 $V[K]$
, for all ordinals
$V[K]$
, for all ordinals
 $\rho < \tau $
, there is a generic
$\rho < \tau $
, there is a generic
 $\nu ^+$
-supercompactness embedding
$\nu ^+$
-supercompactness embedding
 $j_{\rho +2}$
with domain
$j_{\rho +2}$
with domain
 $V[K]$
and critical point
$V[K]$
and critical point
 $\kappa _{\rho +2}$
, added by a poset
$\kappa _{\rho +2}$
, added by a poset
 $\mathbb {F}$
such that the full support power
$\mathbb {F}$
such that the full support power
 $\mathbb {F}^{\kappa _\rho }$
is
$\mathbb {F}^{\kappa _\rho }$
is
 $<\kappa _{\rho }$
-distributive in
$<\kappa _{\rho }$
-distributive in
 $V[K]$
.
$V[K]$
.
Then there is
![]() $\mu \in \operatorname {\mathrm {Index}}$
such that the strong tree property holds at
$\mu \in \operatorname {\mathrm {Index}}$
such that the strong tree property holds at
![]() $\nu ^+$
in the extension of V by
$\nu ^+$
in the extension of V by
![]() $\mathbb {L}_\mu $
.
$\mathbb {L}_\mu $
.
Proof Suppose not. Then for every
![]() $\mu \in \operatorname {\mathrm {Index}}$
, there exists
$\mu \in \operatorname {\mathrm {Index}}$
, there exists
![]() $\lambda \geq \nu ^+$
regular such that there is a thin
$\lambda \geq \nu ^+$
regular such that there is a thin
![]() $\mathcal {P}_{\nu ^+}(\lambda )$
-list with no cofinal branch in the extension of V by
$\mathcal {P}_{\nu ^+}(\lambda )$
-list with no cofinal branch in the extension of V by
![]() $\mathbb {L}_\mu $
. Applying Fact 2.5, by taking an upper bound, we can assume that
$\mathbb {L}_\mu $
. Applying Fact 2.5, by taking an upper bound, we can assume that
![]() $\lambda $
is the same for each
$\lambda $
is the same for each
![]() $\mu $
. Similarly, by increasing
$\mu $
. Similarly, by increasing
![]() $\lambda $
if necessary we can assume that
$\lambda $
if necessary we can assume that
![]() $\lambda ^\nu = \lambda $
. For each
$\lambda ^\nu = \lambda $
. For each
![]() $\mu \in \operatorname {\mathrm {Index}}$
, let
$\mu \in \operatorname {\mathrm {Index}}$
, let
![]() $\dot {d}^\mu $
be a
$\dot {d}^\mu $
be a
![]() $\mathbb {L}_\mu $
-name for a thin
$\mathbb {L}_\mu $
-name for a thin
![]() $\mathcal {P}_{\nu ^+}(\lambda )$
-list forced by the empty condition to have no cofinal branch. Assume that the empty condition in
$\mathcal {P}_{\nu ^+}(\lambda )$
-list forced by the empty condition to have no cofinal branch. Assume that the empty condition in
![]() $\mathbb {L}_\mu $
forces the zth level of
$\mathbb {L}_\mu $
forces the zth level of
![]() $\dot {d}^\mu $
to be indexed by
$\dot {d}^\mu $
to be indexed by
![]() $\langle \dot {\sigma }_z^\mu (\zeta ) \mid \zeta < \nu \rangle $
. We work in
$\langle \dot {\sigma }_z^\mu (\zeta ) \mid \zeta < \nu \rangle $
. We work in
![]() $V[K]$
. Note that
$V[K]$
. Note that
![]() $\lambda $
is collapsed, but we can still examine cofinal branches through a thin
$\lambda $
is collapsed, but we can still examine cofinal branches through a thin
![]() $\mathcal {P}_{\nu ^+}(\lambda )$
-list when
$\mathcal {P}_{\nu ^+}(\lambda )$
-list when
![]() $\lambda $
is merely an ordinal. In fact, since
$\lambda $
is merely an ordinal. In fact, since
![]() $\lambda $
has cardinality and cofinality
$\lambda $
has cardinality and cofinality
![]() $\nu ^+$
,
$\nu ^+$
,
![]() $\mathcal {P}_{\nu ^+}(\lambda )$
is order isomorphic to
$\mathcal {P}_{\nu ^+}(\lambda )$
is order isomorphic to
![]() $\mathcal {P}_{\nu ^+}(\nu ^+)$
. We can thus assume that, in
$\mathcal {P}_{\nu ^+}(\nu ^+)$
. We can thus assume that, in
![]() $V[K]$
,
$V[K]$
,
![]() $\dot {d}^\mu $
is a
$\dot {d}^\mu $
is a
![]() $\mathbb {L}_\mu $
-name for a thin
$\mathbb {L}_\mu $
-name for a thin
![]() $\mathcal {P}_{\nu ^+}(\nu ^+)$
-list. Since
$\mathcal {P}_{\nu ^+}(\nu ^+)$
-list. Since
![]() $\nu ^+$
is cofinal (actually club) in
$\nu ^+$
is cofinal (actually club) in
![]() $\mathcal {P}_{\nu ^+}(\nu ^+)$
, we can further assume that
$\mathcal {P}_{\nu ^+}(\nu ^+)$
, we can further assume that
![]() $\dot {d}^\mu $
is indexed by ordinals.
$\dot {d}^\mu $
is indexed by ordinals.
Let
![]() $I = \{(r, \mu ) \mid \mu \in \operatorname {\mathrm {Index}}, r \in \mathbb {L}_\mu \}$
. For
$I = \{(r, \mu ) \mid \mu \in \operatorname {\mathrm {Index}}, r \in \mathbb {L}_\mu \}$
. For
![]() $s = (r,\mu )$
, let
$s = (r,\mu )$
, let
![]() $R_s$
be the relation
$R_s$
be the relation
![]() $(\alpha , \zeta ) R_s (\beta , \xi )$
iff
$(\alpha , \zeta ) R_s (\beta , \xi )$
iff
![]() $\alpha \leq \beta $
and
$\alpha \leq \beta $
and
![]() $r \Vdash _{\mathbb {L}_{\mu }} \dot {\sigma }^\mu _\alpha (\zeta ) = \dot {\sigma }^\mu _{\beta }(\xi )\cap \alpha $
.
$r \Vdash _{\mathbb {L}_{\mu }} \dot {\sigma }^\mu _\alpha (\zeta ) = \dot {\sigma }^\mu _{\beta }(\xi )\cap \alpha $
.
Let
![]() $X, \bar {V}$
, and
$X, \bar {V}$
, and
![]() $\mathbb {H}$
be as in condition (1), with the function
$\mathbb {H}$
be as in condition (1), with the function
![]() $\mu \mapsto \dot {d}^\mu $
contained in X. Let G be generic for
$\mu \mapsto \dot {d}^\mu $
contained in X. Let G be generic for
![]() $\mathbb {H}$
over
$\mathbb {H}$
over
![]() $V[K]$
, and let
$V[K]$
, and let
![]() $i, L \in V[K][G]$
be as in condition (1). Noting that
$i, L \in V[K][G]$
be as in condition (1). Noting that
![]() $\nu \in i(\operatorname {\mathrm {Index}})$
, we can apply the image of this map to
$\nu \in i(\operatorname {\mathrm {Index}})$
, we can apply the image of this map to
![]() $\nu $
to obtain a
$\nu $
to obtain a
![]() $i(\mathbb {L})(\nu )$
-name for a thin
$i(\mathbb {L})(\nu )$
-name for a thin
![]() $\mathcal {P}_{\nu ^+}(\lambda )$
-list, that we will denote by
$\mathcal {P}_{\nu ^+}(\lambda )$
-list, that we will denote by
![]() $i\dot {d}^\nu $
. Let
$i\dot {d}^\nu $
. Let
![]() $id^\nu = (i\dot {d}^{\nu })_L \in V[K][G]$
, and denote the
$id^\nu = (i\dot {d}^{\nu })_L \in V[K][G]$
, and denote the
![]() $\alpha $
th level with
$\alpha $
th level with
![]() $i\sigma ^\nu _\alpha $
similarly.
$i\sigma ^\nu _\alpha $
similarly.
Let
![]() $\gamma \in i(\nu ^+)$
such that
$\gamma \in i(\nu ^+)$
such that
![]() $\gamma> i"\nu ^+$
. For each
$\gamma> i"\nu ^+$
. For each
![]() $\alpha < \nu ^+$
, there exists
$\alpha < \nu ^+$
, there exists
![]() $\rho _\alpha $
with
$\rho _\alpha $
with
![]() $\rho ' \leq \rho _\alpha < \tau $
and
$\rho ' \leq \rho _\alpha < \tau $
and
![]() $\xi _\alpha < i(\kappa _{\rho _\alpha })$
such that
$\xi _\alpha < i(\kappa _{\rho _\alpha })$
such that
![]() $i\sigma _{i(\alpha )}^\nu (\xi _\alpha ) = i\sigma _\gamma ^\nu (0)\cap i(\alpha )$
. Let
$i\sigma _{i(\alpha )}^\nu (\xi _\alpha ) = i\sigma _\gamma ^\nu (0)\cap i(\alpha )$
. Let
![]() $\dot {\rho }_\alpha $
be an
$\dot {\rho }_\alpha $
be an
![]() $\mathbb {H}$
-name for
$\mathbb {H}$
-name for
![]() $\rho _\alpha $
. Note that the construction of this name does not depend on the choice of generic G, since the existence of such a
$\rho _\alpha $
. Note that the construction of this name does not depend on the choice of generic G, since the existence of such a
![]() $\rho _\alpha $
is forced by the empty condition; the generic is used for notational convenience.
$\rho _\alpha $
is forced by the empty condition; the generic is used for notational convenience.
Working now in
![]() $V[K]$
, for each
$V[K]$
, for each
![]() $\alpha < \nu ^+$
, let
$\alpha < \nu ^+$
, let
![]() $h_\alpha \in \mathbb {H}$
decide the value of
$h_\alpha \in \mathbb {H}$
decide the value of
![]() $\dot {\rho }_\alpha $
to be some ordinal
$\dot {\rho }_\alpha $
to be some ordinal
![]() $\rho _\alpha < \tau $
. Since
$\rho _\alpha < \tau $
. Since
![]() $\tau < \nu ^+$
are both regular, and
$\tau < \nu ^+$
are both regular, and
![]() $\mathbb {H}$
is
$\mathbb {H}$
is
![]() $\nu ^+$
-Knaster, in
$\nu ^+$
-Knaster, in
![]() $V[K]$
we can obtain an unbounded set
$V[K]$
we can obtain an unbounded set
![]() $S \subseteq \nu ^+$
and a fixed
$S \subseteq \nu ^+$
and a fixed
![]() $\rho < \tau $
such that for any
$\rho < \tau $
such that for any
![]() $\alpha ,\beta $
both in S,
$\alpha ,\beta $
both in S,
![]() $h_\alpha $
and
$h_\alpha $
and
![]() $h_{\beta }$
are compatible, and
$h_{\beta }$
are compatible, and
![]() $\rho _\alpha = \rho _{\beta } = \rho $
. Note that by construction,
$\rho _\alpha = \rho _{\beta } = \rho $
. Note that by construction,
![]() $\rho ' \leq \rho $
, so
$\rho ' \leq \rho $
, so
![]() $|\mathbb {L}_\mu | \leq \kappa _\rho $
.
$|\mathbb {L}_\mu | \leq \kappa _\rho $
.
Lemma 3.15.
![]() $\langle R_s \rangle _{s \in I}$
is a system on
$\langle R_s \rangle _{s \in I}$
is a system on
![]() $S \times \kappa _\rho $
.
$S \times \kappa _\rho $
.
Proof The first two conditions are trivial, so it suffices to verify the third. Let
![]() $\alpha < \beta \in S$
. Let p be a common extension of
$\alpha < \beta \in S$
. Let p be a common extension of
![]() $h_\alpha $
and
$h_\alpha $
and
![]() $h_\beta $
, and let G be a generic for
$h_\beta $
, and let G be a generic for
![]() $\mathbb {H}$
over
$\mathbb {H}$
over
![]() $V[K]$
containing p. Work in
$V[K]$
containing p. Work in
![]() $V[K][G]$
. Then there exist
$V[K][G]$
. Then there exist
![]() $\zeta , \xi < i(\kappa _\rho )$
such that
$\zeta , \xi < i(\kappa _\rho )$
such that
![]() $i\sigma ^\nu _{i(\alpha )}(\zeta ) = i\sigma ^\nu _\gamma (0) \cap i(\alpha )$
and
$i\sigma ^\nu _{i(\alpha )}(\zeta ) = i\sigma ^\nu _\gamma (0) \cap i(\alpha )$
and
![]() $i\sigma ^\nu _{i(\beta )}(\xi ) = i\sigma ^\nu _\gamma (0) \cap i(\beta )$
. We conclude that
$i\sigma ^\nu _{i(\beta )}(\xi ) = i\sigma ^\nu _\gamma (0) \cap i(\beta )$
. We conclude that
![]() $\bar {M}[K^*] \models \exists \mu \in i(\operatorname {\mathrm {Index}}), r\in i\mathbb {L}_{\mu }$
, and
$\bar {M}[K^*] \models \exists \mu \in i(\operatorname {\mathrm {Index}}), r\in i\mathbb {L}_{\mu }$
, and
![]() $\zeta , \xi < i(\kappa _\rho )$
such that
$\zeta , \xi < i(\kappa _\rho )$
such that
![]() $r \Vdash \sigma ^\nu _{i(\alpha )}(\zeta ) = \sigma ^\nu _{i(\beta )}(\xi )\cap i(\alpha )$
. By elementarity, there exist
$r \Vdash \sigma ^\nu _{i(\alpha )}(\zeta ) = \sigma ^\nu _{i(\beta )}(\xi )\cap i(\alpha )$
. By elementarity, there exist
![]() $\mu \in \operatorname {\mathrm {Index}}, r\in \mathbb {L}_{\mu }$
, and
$\mu \in \operatorname {\mathrm {Index}}, r\in \mathbb {L}_{\mu }$
, and
![]() $\zeta , \xi < \kappa _\rho $
such that
$\zeta , \xi < \kappa _\rho $
such that
![]() $r \Vdash \sigma ^\mu _\alpha (\zeta )= \sigma ^\mu _{\beta }(\xi )\cap \alpha $
. In particular, letting
$r \Vdash \sigma ^\mu _\alpha (\zeta )= \sigma ^\mu _{\beta }(\xi )\cap \alpha $
. In particular, letting
![]() $s = (r,\mu )$
, we have that
$s = (r,\mu )$
, we have that
![]() $(\alpha , \zeta ) R_s (\beta , \xi )$
.
$(\alpha , \zeta ) R_s (\beta , \xi )$
.
Lemma 3.16. There exists
![]() $s \in I$
such that
$s \in I$
such that
![]() $R_s$
has a cofinal branch.
$R_s$
has a cofinal branch.
Proof By assumption, we have a generic
![]() $\nu ^+$
-supercompactness embedding j with domain
$\nu ^+$
-supercompactness embedding j with domain
![]() $V[K]$
and critical point
$V[K]$
and critical point
![]() $\kappa _{\rho +3}$
, added by a poset
$\kappa _{\rho +3}$
, added by a poset
![]() $\mathbb {F}$
with generic F whose full support power is
$\mathbb {F}$
with generic F whose full support power is
![]() $<\kappa _{\rho +1}$
-distributive in V. In particular, this power is
$<\kappa _{\rho +1}$
-distributive in V. In particular, this power is
![]() $<\kappa _{\rho +1}$
-distributive in
$<\kappa _{\rho +1}$
-distributive in
![]() $V[K]$
, so it satisfies hypothesis (2) of Lemma 2.22. Recall that
$V[K]$
, so it satisfies hypothesis (2) of Lemma 2.22. Recall that
![]() $|\mathbb {L}_\mu | < \kappa _0$
. We can assume that the underlying set of
$|\mathbb {L}_\mu | < \kappa _0$
. We can assume that the underlying set of
![]() $\mathbb {L}_\mu $
is an ordinal below the critical point of j, so that j fixes
$\mathbb {L}_\mu $
is an ordinal below the critical point of j, so that j fixes
![]() $\mathbb {L}_\mu $
pointwise.
$\mathbb {L}_\mu $
pointwise.
Work in
![]() $V[K][F]$
. Let
$V[K][F]$
. Let
![]() $\gamma ' \in j(S)$
such that
$\gamma ' \in j(S)$
such that
![]() $\gamma '> \sup j"\nu ^+$
. For each
$\gamma '> \sup j"\nu ^+$
. For each
![]() $\delta < \kappa _\rho $
and
$\delta < \kappa _\rho $
and
![]() $s = (\mu , p) \in I,$
we define
$s = (\mu , p) \in I,$
we define
We claim that
![]() $\langle b_{s,\delta } \mid s\in I, \delta < \kappa _\rho \rangle $
is a system of branches through
$\langle b_{s,\delta } \mid s\in I, \delta < \kappa _\rho \rangle $
is a system of branches through
![]() $\langle R_s\rangle _{s\in I}$
. By construction, each
$\langle R_s\rangle _{s\in I}$
. By construction, each
![]() $b_{s,\delta }$
is linearly ordered and downwards closed. It remains to verify that
$b_{s,\delta }$
is linearly ordered and downwards closed. It remains to verify that
![]() $\bigcup \operatorname {\mathrm {dom}}(b_s,\delta ) = S$
. Since
$\bigcup \operatorname {\mathrm {dom}}(b_s,\delta ) = S$
. Since
![]() $\kappa _\rho < \operatorname {\mathrm {crit}}(j)$
, and
$\kappa _\rho < \operatorname {\mathrm {crit}}(j)$
, and
![]() $\langle R_s\rangle _{s\in I}$
is a system, we can apply elementarity to conclude that for all
$\langle R_s\rangle _{s\in I}$
is a system, we can apply elementarity to conclude that for all
![]() $\alpha \in S$
there exist
$\alpha \in S$
there exist
![]() $\zeta , \delta < \kappa _\rho $
and
$\zeta , \delta < \kappa _\rho $
and
![]() $s = (\mu , p) \in j(I) = I$
such that
$s = (\mu , p) \in j(I) = I$
such that
In particular,
![]() $\bigcup \operatorname {\mathrm {dom}}(b_{s,\delta }) = S$
.
$\bigcup \operatorname {\mathrm {dom}}(b_{s,\delta }) = S$
.
Note that this system of branches is in
![]() $V[K][F]$
. Noting that
$V[K][F]$
. Noting that
![]() $|I| \leq \kappa _\rho $
, we apply Lemma 2.22, we conclude that there is some
$|I| \leq \kappa _\rho $
, we apply Lemma 2.22, we conclude that there is some
![]() $(s, \delta ) \in I \times \kappa _{\rho }$
such that
$(s, \delta ) \in I \times \kappa _{\rho }$
such that
![]() $b_{s,\delta }$
is cofinal and belongs to
$b_{s,\delta }$
is cofinal and belongs to
![]() $V[K]$
.
$V[K]$
.
Now we finish the proof. Let
![]() $b_{s,\delta }$
be the cofinal branch from the previous lemma, with
$b_{s,\delta }$
be the cofinal branch from the previous lemma, with
![]() $s = (\mu , p)$
, and let L be generic for
$s = (\mu , p)$
, and let L be generic for
![]() $\mathbb {L}_\mu $
containing p. We define an
$\mathbb {L}_\mu $
containing p. We define an
![]() $\mathbb {L}_\mu $
-name
$\mathbb {L}_\mu $
-name
![]() $\dot {\pi }_{s,\delta } = \bigcup \{\dot {\sigma }_\alpha ^\mu (\zeta ) \mid (\alpha , \zeta ) \in b_{s,\delta }\}$
. Since
$\dot {\pi }_{s,\delta } = \bigcup \{\dot {\sigma }_\alpha ^\mu (\zeta ) \mid (\alpha , \zeta ) \in b_{s,\delta }\}$
. Since
![]() $b_{s,\delta }$
is a cofinal branch through
$b_{s,\delta }$
is a cofinal branch through
![]() $R_s$
,
$R_s$
,
![]() $\dot {\pi }_{s,\delta }$
will be a cofinal branch through
$\dot {\pi }_{s,\delta }$
will be a cofinal branch through
![]() $d^\mu $
in
$d^\mu $
in
![]() $V[K][L]$
.
$V[K][L]$
.
Since
![]() $\mathbb {K}$
is
$\mathbb {K}$
is
![]() $\kappa _{\rho '}$
-closed in V, and
$\kappa _{\rho '}$
-closed in V, and
![]() $\mathbb {L}_\mu $
is
$\mathbb {L}_\mu $
is
![]() $\kappa _{\rho '}$
-cc, by Lemma 2.20 we see that
$\kappa _{\rho '}$
-cc, by Lemma 2.20 we see that
![]() $\mathbb {K}$
is forced by
$\mathbb {K}$
is forced by
![]() $\mathbb {L}_\mu $
to have the thin
$\mathbb {L}_\mu $
to have the thin
![]() $\nu ^+$
-approximation property. It follows that
$\nu ^+$
-approximation property. It follows that
![]() $\mathbb {K}$
could not have added a cofinal branch to
$\mathbb {K}$
could not have added a cofinal branch to
![]() $V[L]$
, so
$V[L]$
, so
![]() $d^\mu $
must have a cofinal branch in
$d^\mu $
must have a cofinal branch in
![]() $V[L]$
, contradicting our original assumption.
$V[L]$
, contradicting our original assumption.
3.3. ITP below
 $\aleph _{\omega }$
$\aleph _{\omega }$
Next, we show that in this model, we have ITP at
![]() $\aleph _n$
for all
$\aleph _n$
for all
![]() $n \geq 2$
. The argument follows that of [Reference Neeman14, Section 4], using the stronger branch preservation lemmas described in Section 2.
$n \geq 2$
. The argument follows that of [Reference Neeman14, Section 4], using the stronger branch preservation lemmas described in Section 2.
Theorem 3.17. In the model
![]() $V[A][U][S][e]$
,
$V[A][U][S][e]$
,
![]() $\operatorname {\mathrm {ITP}}$
holds at
$\operatorname {\mathrm {ITP}}$
holds at
![]() $\aleph _{n+2}$
for all n.
$\aleph _{n+2}$
for all n.
Proof Let
![]() $d = \langle d_z \mid z \in (\mathcal {P}_{\kappa _{n+2}}(\lambda ))^{V[A][U][S][e]} \rangle $
be a thin
$d = \langle d_z \mid z \in (\mathcal {P}_{\kappa _{n+2}}(\lambda ))^{V[A][U][S][e]} \rangle $
be a thin
![]() $\mathcal {P}_{\kappa _{n+2}}(\lambda )$
list in
$\mathcal {P}_{\kappa _{n+2}}(\lambda )$
list in
![]() $V[A][U][S][e]$
. We wish to show that it has an ineffable branch.
$V[A][U][S][e]$
. We wish to show that it has an ineffable branch.
We repeat the argument of [Reference Neeman14], examining in particular the proof of [Reference Neeman14, Theorem 4.29]. This construction will produce a lifted
![]() $\lambda $
-supercompactness embedding with critical point
$\lambda $
-supercompactness embedding with critical point
![]() $\kappa _{n+2}$
contained in an extension of
$\kappa _{n+2}$
contained in an extension of
![]() $V[A][U][S][e]$
. We record the definition and some properties of the forcings used to produce this embedding. A detailed exposition can be found in [Reference Neeman14, Section 4].
$V[A][U][S][e]$
. We record the definition and some properties of the forcings used to produce this embedding. A detailed exposition can be found in [Reference Neeman14, Section 4].
Let
![]() $F = A\upharpoonright \kappa _{n+2} \ast U\upharpoonright \kappa _{n+2}$
. Let
$F = A\upharpoonright \kappa _{n+2} \ast U\upharpoonright \kappa _{n+2}$
. Let
![]() $\mathbb {P}_1$
be the factor forcing refining
$\mathbb {P}_1$
be the factor forcing refining
![]() $U\upharpoonright [\kappa _{n+2}, \nu )$
to a generic
$U\upharpoonright [\kappa _{n+2}, \nu )$
to a generic
![]() $G_1$
for
$G_1$
for
![]() $\mathbb {B}^{+F}\upharpoonright [\kappa _{n+2}, \nu )$
, and let
$\mathbb {B}^{+F}\upharpoonright [\kappa _{n+2}, \nu )$
, and let
![]() $\mathbb {P}_2$
be the factor forcing refining
$\mathbb {P}_2$
be the factor forcing refining
![]() $S\upharpoonright [\kappa _{n+2}, \nu )$
to a generic
$S\upharpoonright [\kappa _{n+2}, \nu )$
to a generic
![]() $G_2$
for
$G_2$
for
![]() $\mathbb {C}^{+F}\upharpoonright [\kappa _{n+2}, \nu )$
.
$\mathbb {C}^{+F}\upharpoonright [\kappa _{n+2}, \nu )$
.
Proposition 3.18. There exists a generic
![]() $\lambda $
-supercompactness embedding
$\lambda $
-supercompactness embedding
with critical point
![]() $\kappa _{n+2}$
, contained in the extension of
$\kappa _{n+2}$
, contained in the extension of
![]() $V[A][U_{[0,n]}][G_1][G_2]$
by the product of
$V[A][U_{[0,n]}][G_1][G_2]$
by the product of
![]() $\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V$
and
$\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V$
and
![]() $\operatorname {\mathrm {Add}}(\kappa _{n+1}, \pi (\kappa _{n+3}))^V$
.
$\operatorname {\mathrm {Add}}(\kappa _{n+1}, \pi (\kappa _{n+3}))^V$
.
Proof
![]() $\mathbb {B}^{+F}\upharpoonright [\kappa _{n+2},\nu )$
and
$\mathbb {B}^{+F}\upharpoonright [\kappa _{n+2},\nu )$
and
![]() $\mathbb {C}^{+F}\upharpoonright [\kappa _{n+2},\nu )$
are in
$\mathbb {C}^{+F}\upharpoonright [\kappa _{n+2},\nu )$
are in
![]() $V[F]$
, and by Facts 3.5 and 3.11 they are
$V[F]$
, and by Facts 3.5 and 3.11 they are
![]() $<\kappa _{n+2}$
directed closed in
$<\kappa _{n+2}$
directed closed in
![]() $V[F]$
. So using Fact 3.6, we obtain the desired embedding.
$V[F]$
. So using Fact 3.6, we obtain the desired embedding.
Consider the map
![]() $\beta \mapsto \mathbb {C}^{+A\upharpoonright \beta \ast U\upharpoonright \kappa _{n+1}}\upharpoonright [\beta , \kappa _{n+2})$
described in the second part of Fact 3.11, defined for
$\beta \mapsto \mathbb {C}^{+A\upharpoonright \beta \ast U\upharpoonright \kappa _{n+1}}\upharpoonright [\beta , \kappa _{n+2})$
described in the second part of Fact 3.11, defined for
![]() $\beta \in (\kappa _{n+1}, \kappa _{n+2})$
. Note that the image of
$\beta \in (\kappa _{n+1}, \kappa _{n+2})$
. Note that the image of
![]() $\beta $
under this map is in
$\beta $
under this map is in
![]() $V[A\upharpoonright \beta ][ U\upharpoonright \kappa _{n+1}].$
Consider the image of this map under
$V[A\upharpoonright \beta ][ U\upharpoonright \kappa _{n+1}].$
Consider the image of this map under
![]() $\pi $
; this takes each
$\pi $
; this takes each
![]() $\beta \in (\kappa _{n+1}, \pi (\kappa _{n+2}))$
to a forcing contained in
$\beta \in (\kappa _{n+1}, \pi (\kappa _{n+2}))$
to a forcing contained in
![]() $V^*[A^*\upharpoonright \beta ][ U^*\upharpoonright \kappa _{n+1}]$
. Let
$V^*[A^*\upharpoonright \beta ][ U^*\upharpoonright \kappa _{n+1}]$
. Let
![]() $\mathbb {P}_3$
denote the image of
$\mathbb {P}_3$
denote the image of
![]() $\kappa _{n+2}$
under this new map; i.e.,
$\kappa _{n+2}$
under this new map; i.e.,
![]() $\mathbb {P}_3 = \pi (\mathbb {C})^{+A\upharpoonright \kappa _{n+2}\ast U\upharpoonright \kappa _{n+1}}\upharpoonright [\kappa _{n+2}, \pi (\kappa _{n+2}))$
. Note that
$\mathbb {P}_3 = \pi (\mathbb {C})^{+A\upharpoonright \kappa _{n+2}\ast U\upharpoonright \kappa _{n+1}}\upharpoonright [\kappa _{n+2}, \pi (\kappa _{n+2}))$
. Note that
![]() $\mathbb {P}_3 \in V^*[A^*\upharpoonright \kappa _{n+2}][U^*\upharpoonright \kappa _{n+1}] = V^*[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
. Since
$\mathbb {P}_3 \in V^*[A^*\upharpoonright \kappa _{n+2}][U^*\upharpoonright \kappa _{n+1}] = V^*[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
. Since
![]() $V^* \subseteq V[A_{[n+2, \omega )}]$
(see the proof of [Reference Neeman14, Lemma 4.12]), we conclude that
$V^* \subseteq V[A_{[n+2, \omega )}]$
(see the proof of [Reference Neeman14, Lemma 4.12]), we conclude that
![]() $\mathbb {P}_3 \in V[A_{[n+2, \omega )}][A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
, so in particular
$\mathbb {P}_3 \in V[A_{[n+2, \omega )}][A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
, so in particular
![]() $\mathbb {P}_3\in V[A][U][S][e]$
. Let
$\mathbb {P}_3\in V[A][U][S][e]$
. Let
![]() $G_3$
be generic for
$G_3$
be generic for
![]() $\mathbb {P}_3$
over
$\mathbb {P}_3$
over
![]() $V[A][U][S][e]$
.
$V[A][U][S][e]$
.
Proposition 3.19. The embedding
![]() $\pi $
restricts to an embedding from
$\pi $
restricts to an embedding from
![]() $V[A][U][S_{[n+1,\omega )}]$
to
$V[A][U][S_{[n+1,\omega )}]$
to
![]() $V^*[A^*][U^*][S^*_{[n+1,\omega )}];$
this restriction extends to an embedding from
$V^*[A^*][U^*][S^*_{[n+1,\omega )}];$
this restriction extends to an embedding from
![]() $V[A][U][S][e]$
to
$V[A][U][S][e]$
to
![]() $V^*[A^*][U^*][S^*][e]\ (which\ we\ will\ also\ denote\ by\ \pi )$
. This embedding is contained in the generic extension of
$V^*[A^*][U^*][S^*][e]\ (which\ we\ will\ also\ denote\ by\ \pi )$
. This embedding is contained in the generic extension of
![]() $V[A][U][S][e]$
by the product of
$V[A][U][S][e]$
by the product of
![]() $\mathbb {P}_1$
,
$\mathbb {P}_1$
,
![]() $\mathbb {P}_2$
,
$\mathbb {P}_2$
,
![]() $\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V$
,
$\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V$
,
![]() $\operatorname {\mathrm {Add}}(\kappa _{n+1}, \pi (\kappa _{n+3}))^V$
, and
$\operatorname {\mathrm {Add}}(\kappa _{n+1}, \pi (\kappa _{n+3}))^V$
, and
![]() $\mathbb {P}_3$
.
$\mathbb {P}_3$
.
Proof Let
![]() $U^*_{[n+1,\omega )}$
be the upwards closure of
$U^*_{[n+1,\omega )}$
be the upwards closure of
![]() $G^*_1$
in
$G^*_1$
in
![]() $\pi (\mathbb {U}_{[n+1,\omega )})$
. It is generic for
$\pi (\mathbb {U}_{[n+1,\omega )})$
. It is generic for
![]() $\pi (\mathbb {U}_{[n+1,\omega )})$
over
$\pi (\mathbb {U}_{[n+1,\omega )})$
over
![]() $V^*[A^*][U^*][S^*_{[n+1,\omega )}]$
. Let
$V^*[A^*][U^*][S^*_{[n+1,\omega )}]$
. Let
![]() $U^*$
be the concatenation of
$U^*$
be the concatenation of
![]() $U^*_{[0,n]}$
and
$U^*_{[0,n]}$
and
![]() $U^*_{[n+1,\omega )}$
. Then
$U^*_{[n+1,\omega )}$
. Then
![]() $U^*$
is generic for
$U^*$
is generic for
![]() $\pi (\mathbb {U})$
over
$\pi (\mathbb {U})$
over
![]() $V^*[A^*]$
, and
$V^*[A^*]$
, and
![]() $G^*_2$
is generic over
$G^*_2$
is generic over
![]() $V[A^*][U^*]$
. We can restrict
$V[A^*][U^*]$
. We can restrict
![]() $\pi $
to an embedding (in a mild abuse of notation, we will denote all restrictions and extensions by
$\pi $
to an embedding (in a mild abuse of notation, we will denote all restrictions and extensions by
![]() $\pi $
) from
$\pi $
) from
![]() $V[A][U][G_2]$
to
$V[A][U][G_2]$
to
![]() $V^*[A^*][U^*][G_2^*]$
.
$V^*[A^*][U^*][G_2^*]$
.
Let
![]() $S^*_{[n+1,\omega )}$
be the upwards closure of
$S^*_{[n+1,\omega )}$
be the upwards closure of
![]() $G_2^*$
in
$G_2^*$
in
![]() $\pi (\mathbb {C})^{+A^*\ast U^*}_{[n+1,\omega )}$
. As before we can restrict
$\pi (\mathbb {C})^{+A^*\ast U^*}_{[n+1,\omega )}$
. As before we can restrict
![]() $\pi $
further to an embedding from
$\pi $
further to an embedding from
![]() $V[A][U][S_{[n+1,\omega )}]$
to
$V[A][U][S_{[n+1,\omega )}]$
to
![]() $V^*[A^*][U^*][S^*_{[n+1,\omega )}]$
. Noting that e and
$V^*[A^*][U^*][S^*_{[n+1,\omega )}]$
. Noting that e and
![]() $S_{[0,n-1]}$
are generic for forcings of size less than
$S_{[0,n-1]}$
are generic for forcings of size less than
![]() $\kappa _{n+2}$
, and are thus below the critical point of
$\kappa _{n+2}$
, and are thus below the critical point of
![]() $\pi $
, without any further forcing we can extend
$\pi $
, without any further forcing we can extend
![]() $\pi $
to an embedding from
$\pi $
to an embedding from
![]() $V[A][U][S_{[n+1,\omega )}][S_{[0,n-1]}][e]$
to
$V[A][U][S_{[n+1,\omega )}][S_{[0,n-1]}][e]$
to
![]() $V^*[A^*][U^*][S^*_{[n+1,\omega )}][S_{[0,n-1]}][e].$
$V^*[A^*][U^*][S^*_{[n+1,\omega )}][S_{[0,n-1]}][e].$
Finally, let
![]() $G_3^+$
be the upwards closure of
$G_3^+$
be the upwards closure of
![]() $G_3$
in
$G_3$
in
![]() $\pi (\mathbb {C}_n)^{+A^*\ast U^*}\upharpoonright [\kappa _{n+2}, \pi (\kappa _{n+2}))$
. Let
$\pi (\mathbb {C}_n)^{+A^*\ast U^*}\upharpoonright [\kappa _{n+2}, \pi (\kappa _{n+2}))$
. Let
![]() $S^*_n = S_n \times G_3^+$
. This is generic for
$S^*_n = S_n \times G_3^+$
. This is generic for
![]() $\pi (\mathbb {C}_n^{+A\ast U}) = \pi (\mathbb {C}_n)^{+A^*\ast U^*}$
. We can extend
$\pi (\mathbb {C}_n^{+A\ast U}) = \pi (\mathbb {C}_n)^{+A^*\ast U^*}$
. We can extend
![]() $\pi $
to an embedding from
$\pi $
to an embedding from
![]() $V[A][U][S][e] = V[A][U][S_{[n+1,\omega )}][S_{[0,n-1]}][e][S_n]$
to
$V[A][U][S][e] = V[A][U][S_{[n+1,\omega )}][S_{[0,n-1]}][e][S_n]$
to
![]() $V[A^*][U^*][S^*_{[n+1,\omega )}][S_{[0,n-1]}][e][S^*_n] = V^*[A^*][U^*][S^*][e].$
$V[A^*][U^*][S^*_{[n+1,\omega )}][S_{[0,n-1]}][e][S^*_n] = V^*[A^*][U^*][S^*][e].$
Let
![]() $\hat {A}_{n}$
be a generic filter for
$\hat {A}_{n}$
be a generic filter for
![]() $\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V$
and let
$\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V$
and let
![]() $\hat {A}_{n+1}$
be generic for
$\hat {A}_{n+1}$
be generic for
![]() $\operatorname {\mathrm {Add}}(\kappa _{n+1}, \pi (\kappa _{n+3}))^V$
. Since all posets are contained in
$\operatorname {\mathrm {Add}}(\kappa _{n+1}, \pi (\kappa _{n+3}))^V$
. Since all posets are contained in
![]() $V[A][U][S][e]$
, we can add them in any order. We will add
$V[A][U][S][e]$
, we can add them in any order. We will add
![]() $\hat {A}_{n+1}$
first, followed by
$\hat {A}_{n+1}$
first, followed by
![]() $G_1 \times G_2 \times G_3$
and then
$G_1 \times G_2 \times G_3$
and then
![]() $\hat {A}_n$
.
$\hat {A}_n$
.
Since the posets adding the embedding are not defined over the full model, we need some facts about the construction to determine their properties.
Fact 3.20 [Reference Neeman14, Lemma 4.26].
For all
![]() $n<\omega $
, all sequences of ordinals of length
$n<\omega $
, all sequences of ordinals of length
![]() $<\kappa _{n+1}$
in
$<\kappa _{n+1}$
in
![]() $V[A][U][S][e]$
belong to
$V[A][U][S][e]$
belong to
![]() $V[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}][S\upharpoonright \kappa _{n+1}][e]$
.
$V[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}][S\upharpoonright \kappa _{n+1}][e]$
.
Fact 3.21 [Reference Neeman14, Remark 4.27].
If a forcing
![]() $\mathbb {Q}$
is
$\mathbb {Q}$
is
![]() $\kappa _{n+1}$
-closed in V, then it is
$\kappa _{n+1}$
-closed in V, then it is
![]() $<\kappa _{n+1}$
-distributive over
$<\kappa _{n+1}$
-distributive over
![]() $V[A][U][S][e]$
.
$V[A][U][S][e]$
.
With these facts in hand, we record some properties of these posets.
Proposition 3.22 [Reference Neeman14, Claims 4.30 and 4.31].
![]() $\mathbb {P}_1$
,
$\mathbb {P}_1$
,
![]() $\mathbb {P}_2$
, and
$\mathbb {P}_2$
, and
![]() $\mathbb {P}_3$
are
$\mathbb {P}_3$
are
![]() $\kappa _{n+1}$
closed in
$\kappa _{n+1}$
closed in
![]() $V[A][U][S\upharpoonright [\kappa _{n+1},\nu )][\hat {A}_{n+1}]$
.
$V[A][U][S\upharpoonright [\kappa _{n+1},\nu )][\hat {A}_{n+1}]$
.
Proof First we show that each poset is closed in
![]() $V[A][U][S\upharpoonright [\kappa _{n+1},\nu )]$
.
$V[A][U][S\upharpoonright [\kappa _{n+1},\nu )]$
.
By Fact 3.5, every decreasing sequence of
![]() $\mathbb {P}_1$
with length
$\mathbb {P}_1$
with length
![]() $<\kappa _{n+2}$
in
$<\kappa _{n+2}$
in
![]() $V[F]$
has a lower bound. By Fact 3.20, every decreasing sequence of length
$V[F]$
has a lower bound. By Fact 3.20, every decreasing sequence of length
![]() $<\kappa _{n+1}$
belonging to
$<\kappa _{n+1}$
belonging to
![]() $V[A][U][S\upharpoonright [\kappa _{n+1}, \nu )]$
must be in
$V[A][U][S\upharpoonright [\kappa _{n+1}, \nu )]$
must be in
![]() $V[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}][S\upharpoonright \kappa _{n+1}]$
. The sequence came from
$V[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}][S\upharpoonright \kappa _{n+1}]$
. The sequence came from
![]() $V[A][U][S\upharpoonright [\kappa _{n+1}, \nu )]$
, and that model and
$V[A][U][S\upharpoonright [\kappa _{n+1}, \nu )]$
, and that model and
![]() $V[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}][S\upharpoonright \kappa _{n+1}]$
are mutually generic extensions of
$V[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}][S\upharpoonright \kappa _{n+1}]$
are mutually generic extensions of
![]() $V[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
. Since the sequence is present in both models, it must be be in
$V[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
. Since the sequence is present in both models, it must be be in
![]() $V[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}] \subseteq V[F],$
and thus have a lower bound in
$V[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}] \subseteq V[F],$
and thus have a lower bound in
![]() $\mathbb {P}_1$
. We conclude that
$\mathbb {P}_1$
. We conclude that
![]() $\mathbb {P}_1$
is
$\mathbb {P}_1$
is
![]() $\kappa _{n+1}$
-closed in
$\kappa _{n+1}$
-closed in
![]() $V[A][U][S\upharpoonright [\kappa _{n+1},\nu )]$
as desired.
$V[A][U][S\upharpoonright [\kappa _{n+1},\nu )]$
as desired.
The proof for
![]() $\mathbb {P}_2$
is analogous, using Fact 3.11 in place of Fact 3.5.
$\mathbb {P}_2$
is analogous, using Fact 3.11 in place of Fact 3.5.
Finally we verify that
![]() $\mathbb {P}_3$
is closed. By the second part of Fact 3.11 applied in
$\mathbb {P}_3$
is closed. By the second part of Fact 3.11 applied in
![]() $V^*[A^*][U^*]$
,
$V^*[A^*][U^*]$
,
![]() $\mathbb {P}_3$
is
$\mathbb {P}_3$
is
![]() $\kappa _{n+1}$
-closed in
$\kappa _{n+1}$
-closed in
![]() $V^*[A^*\upharpoonright \kappa _{n+2}][U^*\upharpoonright \kappa _{n+1}] = V^*[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
.
$V^*[A^*\upharpoonright \kappa _{n+2}][U^*\upharpoonright \kappa _{n+1}] = V^*[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
.
![]() $V^*$
is
$V^*$
is
![]() $\kappa _{n+2}$
-closed in
$\kappa _{n+2}$
-closed in
![]() $V[A_{[n+2,\omega )}]$
, so
$V[A_{[n+2,\omega )}]$
, so
![]() $V^*[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
is
$V^*[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
is
![]() $\kappa _{n+2}$
-closed in
$\kappa _{n+2}$
-closed in
![]() $V[A_{[n+2,\omega )}][A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
. We conclude that
$V[A_{[n+2,\omega )}][A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
. We conclude that
![]() $\mathbb {P}_3$
is
$\mathbb {P}_3$
is
![]() $\kappa _{n+1}$
-closed in
$\kappa _{n+1}$
-closed in
![]() $V[A_{[n+2,\omega )}][A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
. By Fact 3.20, any sequence of ordinals of length
$V[A_{[n+2,\omega )}][A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
. By Fact 3.20, any sequence of ordinals of length
![]() $<\kappa _{n+1}$
in
$<\kappa _{n+1}$
in
![]() $V[A][U][S\upharpoonright [\kappa _{n+1},\nu )]$
is in
$V[A][U][S\upharpoonright [\kappa _{n+1},\nu )]$
is in
![]() $V[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
, and thus in
$V[A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
, and thus in
![]() $V[A_{[n+2,\omega )}][A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
. So any descending sequence of conditions of
$V[A_{[n+2,\omega )}][A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+1}]$
. So any descending sequence of conditions of
![]() $\mathbb {P}_3$
that is in
$\mathbb {P}_3$
that is in
![]() $V[A][U][S\upharpoonright [\kappa _{n+1},\nu )]]$
is in
$V[A][U][S\upharpoonright [\kappa _{n+1},\nu )]]$
is in
![]() $V[A_{[n+2,\omega )}][A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+2}]$
, and thus has a lower bound. We conclude that
$V[A_{[n+2,\omega )}][A\upharpoonright \kappa _{n+2}][U\upharpoonright \kappa _{n+2}]$
, and thus has a lower bound. We conclude that
![]() $\mathbb {P}_3$
is
$\mathbb {P}_3$
is
![]() $\kappa _{n+1}$
-closed in
$\kappa _{n+1}$
-closed in
![]() $V[A][U][S\upharpoonright [\kappa _{n+1},\nu )]$
.
$V[A][U][S\upharpoonright [\kappa _{n+1},\nu )]$
.
Since
![]() $\hat {A}_{n+1}$
is
$\hat {A}_{n+1}$
is
![]() $\kappa _{n+1}$
-closed in V, by Fact 3.21 it is
$\kappa _{n+1}$
-closed in V, by Fact 3.21 it is
![]() $\kappa _{n+1}$
-distributive over
$\kappa _{n+1}$
-distributive over
![]() $V[A][U][S\upharpoonright [\kappa _{n+1},\nu )]$
. It follows that
$V[A][U][S\upharpoonright [\kappa _{n+1},\nu )]$
. It follows that
![]() $\mathbb {P}_1$
,
$\mathbb {P}_1$
,
![]() $\mathbb {P}_2$
, and
$\mathbb {P}_2$
, and
![]() $\mathbb {P}_3$
remain
$\mathbb {P}_3$
remain
![]() $\kappa _{n+1}$
-closed in
$\kappa _{n+1}$
-closed in
![]() $V[A][U][S\upharpoonright [\kappa _{n+1},\nu )][\hat {A}_{n+1}]$
.
$V[A][U][S\upharpoonright [\kappa _{n+1},\nu )][\hat {A}_{n+1}]$
.
Proposition 3.23.
![]() $V[A][U][S][e][\hat {A}_{n+1}]$
is a
$V[A][U][S][e][\hat {A}_{n+1}]$
is a
![]() $\kappa _{n+1}$
-cc extension of the model
$\kappa _{n+1}$
-cc extension of the model
![]() $V[A][U][S\upharpoonright [\kappa _{n+1},\nu )][\hat {A}_{n+1}]$
.
$V[A][U][S\upharpoonright [\kappa _{n+1},\nu )][\hat {A}_{n+1}]$
.
Proof The extending poset is
![]() $\mathbb {C}_{[0,n)}^{+A\ast U}\times \operatorname {\mathrm {Col}}(\omega ,\mu )$
. Every piece of this poset has size
$\mathbb {C}_{[0,n)}^{+A\ast U}\times \operatorname {\mathrm {Col}}(\omega ,\mu )$
. Every piece of this poset has size
![]() $<\kappa _{n+1}$
except
$<\kappa _{n+1}$
except
![]() $\mathbb {C}_{n-1}^{+A\ast U}$
, so it is enough to verify that this poset is
$\mathbb {C}_{n-1}^{+A\ast U}$
, so it is enough to verify that this poset is
![]() $\kappa _{n+1}$
-cc. By Fact 3.13, V has the
$\kappa _{n+1}$
-cc. By Fact 3.13, V has the
![]() $<\kappa _{n+1}$
-covering property in
$<\kappa _{n+1}$
-covering property in
![]() $V[A][U][S][e]$
; since
$V[A][U][S][e]$
; since
![]() $\hat {A}_{n+1}$
is
$\hat {A}_{n+1}$
is
![]() $<\kappa _{n+1}$
-distributive, V likewise has the
$<\kappa _{n+1}$
-distributive, V likewise has the
![]() $<\kappa _{n+1}$
-covering property in
$<\kappa _{n+1}$
-covering property in
![]() $V[A][U][S][e][\hat {A}_{n+1}]$
, and thus also in
$V[A][U][S][e][\hat {A}_{n+1}]$
, and thus also in
![]() $V[A][U][S\upharpoonright [\kappa _{n+1},\nu )][\hat {A}_{n+1}]$
. A standard
$V[A][U][S\upharpoonright [\kappa _{n+1},\nu )][\hat {A}_{n+1}]$
. A standard
![]() $\Delta $
-system argument, using Lemma 2.15 and the fact that
$\Delta $
-system argument, using Lemma 2.15 and the fact that
![]() $\kappa _{n+1}$
is inaccessible in
$\kappa _{n+1}$
is inaccessible in
![]() $V[A][U][S\upharpoonright [\kappa _{n+1},\nu )][\hat {A}_{n+1}]$
, yields that the poset has the
$V[A][U][S\upharpoonright [\kappa _{n+1},\nu )][\hat {A}_{n+1}]$
, yields that the poset has the
![]() $\kappa _{n+1}$
chain condition.
$\kappa _{n+1}$
chain condition.
By Lemma 2.6, d has a cofinal branch b in
![]() $V[A][U][S][e][\hat {A}_{n+1}][G_1\times G_2\times G_3][\hat {A}_n]$
, that is ineffable if it is contained in
$V[A][U][S][e][\hat {A}_{n+1}][G_1\times G_2\times G_3][\hat {A}_n]$
, that is ineffable if it is contained in
![]() $V[A][U][S][e]$
. It remains to show that this branch is actually present in
$V[A][U][S][e]$
. It remains to show that this branch is actually present in
![]() $V[A][U][S][e]$
. To do this, we will show that at each stage, the forcing has the appropriate approximation property, and then verify that
$V[A][U][S][e]$
. To do this, we will show that at each stage, the forcing has the appropriate approximation property, and then verify that
![]() $\dot {b}$
is approximated by that forcing.
$\dot {b}$
is approximated by that forcing.
Claim 3.24. The branch b is in
![]() $V[A][U][S][e][\hat {A}_{n+1}][G_1\times G_2\times G_3].$
$V[A][U][S][e][\hat {A}_{n+1}][G_1\times G_2\times G_3].$
Proof First we show that
![]() $\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V$
has the
$\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V$
has the
![]() $\kappa _{n+1}$
-approximation property. Note that
$\kappa _{n+1}$
-approximation property. Note that
![]() $\kappa _{n+2}$
is collapsed in the extension by
$\kappa _{n+2}$
is collapsed in the extension by
![]() $G_1\times G_2 \times G_3$
, since
$G_1\times G_2 \times G_3$
, since
![]() $G_3$
will collapse all cardinals in the interval
$G_3$
will collapse all cardinals in the interval
![]() $[\kappa _{n+2}, \pi (\kappa _{n+2}))$
, but the cofinality of
$[\kappa _{n+2}, \pi (\kappa _{n+2}))$
, but the cofinality of
![]() $\kappa _{n+2}$
in the extension is at least
$\kappa _{n+2}$
in the extension is at least
![]() $\kappa _{n+1}$
.
$\kappa _{n+1}$
.
Since
![]() $V[A][U][S][e][\hat {A}_{n+1}]$
is the extension of
$V[A][U][S][e][\hat {A}_{n+1}]$
is the extension of
![]() $V[A][U][S\upharpoonright [\kappa _{n+1},\nu )][\hat {A}_{n+1}]$
by a
$V[A][U][S\upharpoonright [\kappa _{n+1},\nu )][\hat {A}_{n+1}]$
by a
![]() $\kappa _{n+1}$
-cc forcing, by Lemma 2.10 we see that
$\kappa _{n+1}$
-cc forcing, by Lemma 2.10 we see that
![]() $G_1\times G_2 \times G_3$
doesn’t add any new sequences of ordinals of length
$G_1\times G_2 \times G_3$
doesn’t add any new sequences of ordinals of length
![]() $\kappa _{n+1}$
to
$\kappa _{n+1}$
to
![]() $V[A][U][S][e][\hat {A}_{n+1}]$
. If
$V[A][U][S][e][\hat {A}_{n+1}]$
. If
![]() $n \geq 1$
, by Fact 3.13, V has the
$n \geq 1$
, by Fact 3.13, V has the
![]() $\kappa _{n+1}$
-covering property in
$\kappa _{n+1}$
-covering property in
![]() $V[A][U][S][e][\hat {A}_{n+1}][G_1\times G_2\times G_3].$
Applying Lemma 2.15, we see that
$V[A][U][S][e][\hat {A}_{n+1}][G_1\times G_2\times G_3].$
Applying Lemma 2.15, we see that
![]() $\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2})\cdot 2)^V$
, which is the square of
$\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2})\cdot 2)^V$
, which is the square of
![]() $\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V$
, is
$\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V$
, is
![]() $\kappa _{n+1}$
-cc over this model. Lemma 2.13 gives us that the poset has the
$\kappa _{n+1}$
-cc over this model. Lemma 2.13 gives us that the poset has the
![]() $\kappa _{n+1}$
-approximation property. For
$\kappa _{n+1}$
-approximation property. For
![]() $n=0$
, we see that the square of
$n=0$
, we see that the square of
![]() $\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V$
is
$\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V$
is
![]() $\kappa _1$
-cc in any model where
$\kappa _1$
-cc in any model where
![]() $\kappa _1$
is a cardinal.
$\kappa _1$
is a cardinal.
Let
![]() $\dot {b}$
be a name (in
$\dot {b}$
be a name (in
![]() $V[A][U][S][e]$
) for the branch b. We will verify that
$V[A][U][S][e]$
) for the branch b. We will verify that
![]() $\dot {b}$
is
$\dot {b}$
is
![]() $\kappa _{n+1}$
-approximated by
$\kappa _{n+1}$
-approximated by
![]() $\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V$
over
$\operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V$
over
![]() $V[A][U][S][e][\hat {A}_n][G_1\times G_2 \times G_3]$
. Let W denote
$V[A][U][S][e][\hat {A}_n][G_1\times G_2 \times G_3]$
. Let W denote
![]() $V[A][U][S\upharpoonright [\kappa _{n+1},\nu )][\hat {A}_{n+1}]$
. We note that the product
$V[A][U][S\upharpoonright [\kappa _{n+1},\nu )][\hat {A}_{n+1}]$
. We note that the product
![]() $\mathbb {P}_1 \times \mathbb {P}_2 \times \mathbb {P}_3$
is
$\mathbb {P}_1 \times \mathbb {P}_2 \times \mathbb {P}_3$
is
![]() $\kappa _{n+1}$
-closed in W by Fact 3.22, and
$\kappa _{n+1}$
-closed in W by Fact 3.22, and
![]() $V[A][U][S][e][\hat {A}_{n+1}]$
is a
$V[A][U][S][e][\hat {A}_{n+1}]$
is a
![]() $\kappa _{n+1}$
-cc extension of W by Fact 3.23. Then by Lemma 2.10, forcing with
$\kappa _{n+1}$
-cc extension of W by Fact 3.23. Then by Lemma 2.10, forcing with
![]() $\mathbb {P}_1\times \mathbb {P}_2\times \mathbb {P}_3$
over
$\mathbb {P}_1\times \mathbb {P}_2\times \mathbb {P}_3$
over
![]() $V[A][U][S][e][\hat {A}_{n+1}]$
will not add any sequences of ordinals of length
$V[A][U][S][e][\hat {A}_{n+1}]$
will not add any sequences of ordinals of length
![]() $< \kappa _{n+1}$
.
$< \kappa _{n+1}$
.
By Lemma 2.8, it follows that
![]() $\dot {b}$
is thinly
$\dot {b}$
is thinly
![]() $\kappa _{n+2}$
-approximated by the full forcing
$\kappa _{n+2}$
-approximated by the full forcing
![]() $\operatorname {\mathrm {Add}}(\kappa _{n+1}, \pi (\kappa _{n+2}))^V \times \mathbb {P}_1 \times \mathbb {P}_2 \times \mathbb {P}_3 \times \operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V$
over
$\operatorname {\mathrm {Add}}(\kappa _{n+1}, \pi (\kappa _{n+2}))^V \times \mathbb {P}_1 \times \mathbb {P}_2 \times \mathbb {P}_3 \times \operatorname {\mathrm {Add}}(\kappa _n, \pi (\kappa _{n+2}))^V$
over
![]() $V[A][U][S][e]$
, and thus
$V[A][U][S][e]$
, and thus
![]() $\kappa _{n+1}$
-approximated by the same forcing over
$\kappa _{n+1}$
-approximated by the same forcing over
![]() $V[A][U][S][e]$
. Since the poset
$V[A][U][S][e]$
. Since the poset
![]() $\operatorname {\mathrm {Add}}(\kappa _{n}, \pi (\kappa _{n+3}))^V$
is
$\operatorname {\mathrm {Add}}(\kappa _{n}, \pi (\kappa _{n+3}))^V$
is
![]() $\kappa _{n+1}$
-cc, we can apply Lemma 2.11 to conclude that
$\kappa _{n+1}$
-cc, we can apply Lemma 2.11 to conclude that
![]() $\dot {b}$
is
$\dot {b}$
is
![]() $\kappa _{n+1}$
-approximated over
$\kappa _{n+1}$
-approximated over
![]() $V[A][U][S][e][\hat {A}_{n+1}][G_1\times G_2\times G_3]$
. Thus the branch could not have been added by
$V[A][U][S][e][\hat {A}_{n+1}][G_1\times G_2\times G_3]$
. Thus the branch could not have been added by
![]() $\hat {A}_n$
. We conclude that
$\hat {A}_n$
. We conclude that
![]() $b\in V[A][U][S][e][\hat {A}_{n+1}][G_1\times G_2\times G_3]$
.
$b\in V[A][U][S][e][\hat {A}_{n+1}][G_1\times G_2\times G_3]$
.
Claim 3.25. The branch b is in
![]() $V[A][U][S][e][\hat {A}_{n+1}]$
.
$V[A][U][S][e][\hat {A}_{n+1}]$
.
Proof To show that adding
![]() $G_1\times G_2\times G_3$
does not add a branch, we follow the argument of [Reference Neeman14, Lemma 4.29]. Recall that
$G_1\times G_2\times G_3$
does not add a branch, we follow the argument of [Reference Neeman14, Lemma 4.29]. Recall that
![]() $\mathbb {P}_1\times \mathbb {P}_2 \times \mathbb {P}_3$
is
$\mathbb {P}_1\times \mathbb {P}_2 \times \mathbb {P}_3$
is
![]() $\kappa _{n+1}$
-closed in
$\kappa _{n+1}$
-closed in
![]() $W\mathrel {\mathop :}= V[A][U][S\upharpoonright [\kappa _{n+1},\nu )][\hat {A}_{n+1}]$
, and that
$W\mathrel {\mathop :}= V[A][U][S\upharpoonright [\kappa _{n+1},\nu )][\hat {A}_{n+1}]$
, and that
![]() $V[A][U][S][e][\hat {A}_{n+1}]$
is an extension of W by a
$V[A][U][S][e][\hat {A}_{n+1}]$
is an extension of W by a
![]() $\kappa _{n+1}$
-cc poset. Note also that
$\kappa _{n+1}$
-cc poset. Note also that
![]() $2^{\kappa _n}> \kappa _{n+1}$
in W. By Lemma 2.16,
$2^{\kappa _n}> \kappa _{n+1}$
in W. By Lemma 2.16,
![]() $V[A][U][S][e][\hat {A}_{n+1}][G_1\times G_2\times G_3]$
has the thin
$V[A][U][S][e][\hat {A}_{n+1}][G_1\times G_2\times G_3]$
has the thin
![]() $\kappa _{n+2}$
-approximation property over
$\kappa _{n+2}$
-approximation property over
![]() $V[A][U][S][e][\hat {A}_{n+1}].$
$V[A][U][S][e][\hat {A}_{n+1}].$
Let
![]() $\dot {b}$
be a
$\dot {b}$
be a
![]() $\mathbb {P}_1\times \mathbb {P}_2\times \mathbb {P}_3$
-name for b. Note that by Lemma 2.8,
$\mathbb {P}_1\times \mathbb {P}_2\times \mathbb {P}_3$
-name for b. Note that by Lemma 2.8,
![]() $\dot {b}$
is thinly
$\dot {b}$
is thinly
![]() $\kappa _{n+2}$
-approximated by the forcing
$\kappa _{n+2}$
-approximated by the forcing
![]() $\operatorname {\mathrm {Add}}(\kappa _{n+1}, \pi (\kappa _{n+3}))^V\times (\mathbb {P}_1\times \mathbb {P}_2\times \mathbb {P}_3)$
over
$\operatorname {\mathrm {Add}}(\kappa _{n+1}, \pi (\kappa _{n+3}))^V\times (\mathbb {P}_1\times \mathbb {P}_2\times \mathbb {P}_3)$
over
![]() $V[A][U][S][e].$
Since
$V[A][U][S][e].$
Since
![]() $\operatorname {\mathrm {Add}}(\kappa _{n+1},\pi (\kappa _{n+3}))^V$
is
$\operatorname {\mathrm {Add}}(\kappa _{n+1},\pi (\kappa _{n+3}))^V$
is
![]() $\kappa _{n+2}$
-cc, we can apply Lemma 2.9 to see that
$\kappa _{n+2}$
-cc, we can apply Lemma 2.9 to see that
![]() $\dot {b}$
is thinly
$\dot {b}$
is thinly
![]() $\kappa _{n+2}$
-approximated by
$\kappa _{n+2}$
-approximated by
![]() $\mathbb {P}_1\times \mathbb {P}_2\times \mathbb {P}_3$
over
$\mathbb {P}_1\times \mathbb {P}_2\times \mathbb {P}_3$
over
![]() $V[A][U][S][e][\hat {A}_{n+1}]$
. It follows that b cannot have been added by
$V[A][U][S][e][\hat {A}_{n+1}]$
. It follows that b cannot have been added by
![]() $G_1\times G_2\times G_3$
, and so
$G_1\times G_2\times G_3$
, and so
![]() $b \in V[A][U][S][e][\hat {A}_{n+1}]$
.
$b \in V[A][U][S][e][\hat {A}_{n+1}]$
.
Claim 3.26. The branch b is in
![]() $V[A][U][S][e]$
.
$V[A][U][S][e]$
.
Proof Since the square of
![]() $\operatorname {\mathrm {Add}}(\kappa _{n+1},\pi (\kappa _{n+3}))^V$
is
$\operatorname {\mathrm {Add}}(\kappa _{n+1},\pi (\kappa _{n+3}))^V$
is
![]() $\kappa _{n+2}$
-cc over
$\kappa _{n+2}$
-cc over
![]() $V[A][U][S][e]$
, by Lemma 2.13 we see that
$V[A][U][S][e]$
, by Lemma 2.13 we see that
![]() $\operatorname {\mathrm {Add}}(\kappa _{n+1},\pi (\kappa _{n+3}))^V$
has the
$\operatorname {\mathrm {Add}}(\kappa _{n+1},\pi (\kappa _{n+3}))^V$
has the
![]() $\kappa _{n+2}$
-approximation property over
$\kappa _{n+2}$
-approximation property over
![]() $V[A][U][S][e]$
. Let
$V[A][U][S][e]$
. Let
![]() $\dot {b}$
be a
$\dot {b}$
be a
![]() $\operatorname {\mathrm {Add}}(\kappa _{n+1},\pi (\kappa _{n+3}))^V$
-name for b. By Lemma 2.8,
$\operatorname {\mathrm {Add}}(\kappa _{n+1},\pi (\kappa _{n+3}))^V$
-name for b. By Lemma 2.8,
![]() $\dot {b}$
is
$\dot {b}$
is
![]() $\kappa _{n+2}$
-approximated by
$\kappa _{n+2}$
-approximated by
![]() $\operatorname {\mathrm {Add}}(\kappa _{n+1},\pi (\kappa _{n+3}))^V$
over the model
$\operatorname {\mathrm {Add}}(\kappa _{n+1},\pi (\kappa _{n+3}))^V$
over the model
![]() $V[A][U][S][e]$
. Thus
$V[A][U][S][e]$
. Thus
![]() $\hat {A}_{n+1}$
cannot have added the branch, and so
$\hat {A}_{n+1}$
cannot have added the branch, and so
![]() $b \in V[A][U][S][e]$
.
$b \in V[A][U][S][e]$
.
We have shown that the branch b found in the larger model was actually present in the target model
![]() $V[A][U][S][e]$
; as described in Lemma 2.6, b must be ineffable.
$V[A][U][S][e]$
; as described in Lemma 2.6, b must be ineffable.
3.4. The strong tree property up to
 $\aleph _{\omega +1}$
$\aleph _{\omega +1}$
Finally, we put all the pieces together. The argument here is very similar to [Reference Neeman14, Section 6]. We replace [Reference Neeman14, Lemma 3.10] with Theorem 3.14, and modify some details to accommodate the auxiliary collapse.
Theorem 3.27. Let
![]() $\langle \kappa _n\mid 2 \leq n<\omega \rangle $
be an increasing sequence of supercompact cardinals with supremum
$\langle \kappa _n\mid 2 \leq n<\omega \rangle $
be an increasing sequence of supercompact cardinals with supremum
![]() $\nu $
. Then there are generics A for
$\nu $
. Then there are generics A for
![]() $\mathbb {A}$
, U for
$\mathbb {A}$
, U for
![]() $\mathbb {U}$
over
$\mathbb {U}$
over
![]() $V[A]$
, S for
$V[A]$
, S for
![]() $\mathbb {C}^{+A\ast U}$
over
$\mathbb {C}^{+A\ast U}$
over
![]() $V[A][U]$
, and e for
$V[A][U]$
, and e for
![]() $\operatorname {\mathrm {Col}}(\omega , \mu )$
over
$\operatorname {\mathrm {Col}}(\omega , \mu )$
over
![]() $V[A][U][S]$
, such that in the final model
$V[A][U][S]$
, such that in the final model
![]() $V[A][U][S][e]$
we have the following properties
$V[A][U][S][e]$
we have the following properties
![]() $:$
$:$
-
•
 $\aleph _n = \kappa _n$
for all
$\aleph _n = \kappa _n$
for all
 $n < \omega ,$
$n < \omega ,$
-
•
 $\aleph _\omega $
is strong limit,
$\aleph _\omega $
is strong limit, -
•
 $(\nu ^+)^V = \aleph _{\omega +1},$
$(\nu ^+)^V = \aleph _{\omega +1},$
-
• the strong tree property holds at
 $\aleph _{\omega +1},$
$\aleph _{\omega +1},$
-
• ITP holds at
 $\aleph _n$
for
$\aleph _n$
for
 $2 \leq n < \omega $
.
$2 \leq n < \omega $
.
Proof In order to apply Theorem 3.14, we need to separate the pieces of the forcing that depend directly on
![]() $\kappa _1$
. In particular, we wish to examine the forcing with
$\kappa _1$
. In particular, we wish to examine the forcing with
![]() $\operatorname {\mathrm {Add}}(\kappa _1^+, \kappa _3)^V \times \mathbb {C}_0(\kappa _1^+)^{+A_0\ast U_0}\times \operatorname {\mathrm {Col}}(\omega ,\kappa _1)$
removed. Unfortunately
$\operatorname {\mathrm {Add}}(\kappa _1^+, \kappa _3)^V \times \mathbb {C}_0(\kappa _1^+)^{+A_0\ast U_0}\times \operatorname {\mathrm {Col}}(\omega ,\kappa _1)$
removed. Unfortunately
![]() $\mathbb {U}_{[1,\omega )}$
and
$\mathbb {U}_{[1,\omega )}$
and
![]() $\mathbb {C}^{+A\ast U}_{[1,\omega )}$
rely on the generics for the forcings we wish to remove, so we pass to the versions of these posets that do not depend on the earlier generics. To do this, we need the following definition.
$\mathbb {C}^{+A\ast U}_{[1,\omega )}$
rely on the generics for the forcings we wish to remove, so we pass to the versions of these posets that do not depend on the earlier generics. To do this, we need the following definition.
Definition 3.28. Let F be a filter on
![]() $\mathbb {A}\upharpoonright \beta \ast \dot {\mathbb {U}}\upharpoonright \beta $
. Let
$\mathbb {A}\upharpoonright \beta \ast \dot {\mathbb {U}}\upharpoonright \beta $
. Let
![]() $\gamma \leq \nu $
and let B be a filter on
$\gamma \leq \nu $
and let B be a filter on
![]() $\mathbb {B}^{+F}\upharpoonright [\beta ,\gamma )$
. We define a filter
$\mathbb {B}^{+F}\upharpoonright [\beta ,\gamma )$
. We define a filter
![]() $F+B$
on
$F+B$
on
![]() $\mathbb {A}\upharpoonright \gamma \ast \dot {\mathbb {U}}\upharpoonright \gamma $
by
$\mathbb {A}\upharpoonright \gamma \ast \dot {\mathbb {U}}\upharpoonright \gamma $
by
![]() $F+B = \{(a,u) \mid (a,u \upharpoonright \beta )\in F \text { and } u\upharpoonright [\beta ,\gamma )\in B\}$
.
$F+B = \{(a,u) \mid (a,u \upharpoonright \beta )\in F \text { and } u\upharpoonright [\beta ,\gamma )\in B\}$
.
Let
![]() $A_0\ast U_0$
be generic for
$A_0\ast U_0$
be generic for
![]() $\mathbb {A}_0\ast \dot {\mathbb {U}}_0$
over V. Let
$\mathbb {A}_0\ast \dot {\mathbb {U}}_0$
over V. Let
![]() $B_{[1,\omega )}$
be generic for
$B_{[1,\omega )}$
be generic for
![]() $\mathbb {B}_{[1,\omega )}^{+A_0\ast U_0}\upharpoonright [\kappa _2,\nu )$
over
$\mathbb {B}_{[1,\omega )}^{+A_0\ast U_0}\upharpoonright [\kappa _2,\nu )$
over
![]() $V[A_0\ast U_0]$
. Let
$V[A_0\ast U_0]$
. Let
![]() $C_{[1,\omega )}$
be generic for
$C_{[1,\omega )}$
be generic for
![]() $\mathbb {C}^{+A_0\ast U_0+B}\upharpoonright [\kappa _2,\nu )$
over
$\mathbb {C}^{+A_0\ast U_0+B}\upharpoonright [\kappa _2,\nu )$
over
![]() $V[A_0\ast U_0][B_{[1,\omega )}]$
. Let
$V[A_0\ast U_0][B_{[1,\omega )}]$
. Let
![]() $A_{[2,\omega )}$
be generic for
$A_{[2,\omega )}$
be generic for
![]() $\mathbb {A}_{[2,\omega )}$
over
$\mathbb {A}_{[2,\omega )}$
over
![]() $V[A_0\ast U_0][B_{[1,\omega )}][C_{[1,\omega )}].$
Let M denote the model
$V[A_0\ast U_0][B_{[1,\omega )}][C_{[1,\omega )}].$
Let M denote the model
![]() $V[A_{[2,\omega )}][A_0\ast U_0][B_{[1,\omega )}][C_{[1,\omega )}]$
.
$V[A_{[2,\omega )}][A_0\ast U_0][B_{[1,\omega )}][C_{[1,\omega )}]$
.
For each
![]() $\mu \in \operatorname {\mathrm {Index}}$
, let
$\mu \in \operatorname {\mathrm {Index}}$
, let
![]() $\mathbb {L}_\mu $
be the poset
$\mathbb {L}_\mu $
be the poset
![]() $\operatorname {\mathrm {Add}}(\mu ^+, \kappa _3)^V \times \mathbb {C}_0(\mu ^+)^{+A_0\ast U_0}\times \operatorname {\mathrm {Col}}(\omega ,\mu )$
.
$\operatorname {\mathrm {Add}}(\mu ^+, \kappa _3)^V \times \mathbb {C}_0(\mu ^+)^{+A_0\ast U_0}\times \operatorname {\mathrm {Col}}(\omega ,\mu )$
.
![]() $\mathbb {L}_\mu $
is the remaining piece of the forcing that depends on
$\mathbb {L}_\mu $
is the remaining piece of the forcing that depends on
![]() $\kappa _1$
, with
$\kappa _1$
, with
![]() $\mu ^+$
chosen to be the value of
$\mu ^+$
chosen to be the value of
![]() $\kappa _1$
. Recall that
$\kappa _1$
. Recall that
![]() $\kappa _1$
is a parameter in the definition of
$\kappa _1$
is a parameter in the definition of
![]() $\mathbb {C}_0$
, so by
$\mathbb {C}_0$
, so by
![]() $\mathbb {C}_0(\mu ^+)$
we mean
$\mathbb {C}_0(\mu ^+)$
we mean
![]() $\mathbb {C}_0$
defined relative to the parameter
$\mathbb {C}_0$
defined relative to the parameter
![]() $\kappa _1 = \mu ^+$
.
$\kappa _1 = \mu ^+$
.
Let
![]() $\lambda \geq \nu ^+$
such that
$\lambda \geq \nu ^+$
such that
![]() $\lambda ^\nu =\lambda $
. Let K be generic for
$\lambda ^\nu =\lambda $
. Let K be generic for
![]() $\operatorname {\mathrm {Col}}(\nu ^+, \lambda )^{V}$
. Since K is mutually generic with the remaining pieces of the forcing, we have that
$\operatorname {\mathrm {Col}}(\nu ^+, \lambda )^{V}$
. Since K is mutually generic with the remaining pieces of the forcing, we have that
![]() $M[K] = V[K][A_{[2,\omega )}][A_0\ast U_0][B_{[1,\omega )}][C_{[1,\omega )}]$
.
$M[K] = V[K][A_{[2,\omega )}][A_0\ast U_0][B_{[1,\omega )}][C_{[1,\omega )}]$
.
Claim 3.29. In
![]() $V[K][A_{[2,\omega )}]$
, there is a
$V[K][A_{[2,\omega )}]$
, there is a
![]() $\nu ^+$
-supercompactness embedding
$\nu ^+$
-supercompactness embedding
![]() $\pi :V[K][A_{[2,\omega )}] \to V^*[K^*][A^*_{[2,\omega )}]$
with critical point
$\pi :V[K][A_{[2,\omega )}] \to V^*[K^*][A^*_{[2,\omega )}]$
with critical point
![]() $\kappa _2$
and
$\kappa _2$
and
![]() $|\pi (\kappa _2)| = \nu ^{++}$
, such that
$|\pi (\kappa _2)| = \nu ^{++}$
, such that
![]() $\nu \in \pi (\operatorname {\mathrm {Index}})$
. In any extension
$\nu \in \pi (\operatorname {\mathrm {Index}})$
. In any extension
![]() $M[K][\hat {A}_0]$
of
$M[K][\hat {A}_0]$
of
![]() $M[K]$
by the poset
$M[K]$
by the poset
![]() $\operatorname {\mathrm {Add}}(\omega , [\kappa _2, \pi (\kappa _2)))^V$
,
$\operatorname {\mathrm {Add}}(\omega , [\kappa _2, \pi (\kappa _2)))^V$
,
![]() $\pi $
extends to an elementary embedding
$\pi $
extends to an elementary embedding
![]() $\pi :M[K] \to M^*[K^*]$
with
$\pi :M[K] \to M^*[K^*]$
with
![]() $\nu \in \pi (\operatorname {\mathrm {Index}})$
.
$\nu \in \pi (\operatorname {\mathrm {Index}})$
.
Proof The existence of this embedding in
![]() $V[K][A_{[2,\omega )}]$
is immediate from the indestructibility of
$V[K][A_{[2,\omega )}]$
is immediate from the indestructibility of
![]() $\kappa _2$
, noting that
$\kappa _2$
, noting that
![]() $K\times A_{[2,\omega )}$
is generic for a
$K\times A_{[2,\omega )}$
is generic for a
![]() $\kappa _2$
-directed closed forcing. The fact that this embedding extends to have domain
$\kappa _2$
-directed closed forcing. The fact that this embedding extends to have domain
![]() $M[K]$
and the fact that
$M[K]$
and the fact that
![]() $\nu \in \pi (\operatorname {\mathrm {Index}})$
, are analogous to the proof of [Reference Neeman14, Lemma 5.7]. To verify that
$\nu \in \pi (\operatorname {\mathrm {Index}})$
, are analogous to the proof of [Reference Neeman14, Lemma 5.7]. To verify that
![]() $\nu \in \pi (\operatorname {\mathrm {Index}})$
, we can apply the arguments of [Reference Neeman14, Lemma 5.7] in
$\nu \in \pi (\operatorname {\mathrm {Index}})$
, we can apply the arguments of [Reference Neeman14, Lemma 5.7] in
![]() $M[K] = V[K][A_{[2,\omega )}][A_0\ast U_0][B_{[1,\omega )}][C_{[1,\omega )}]$
; since
$M[K] = V[K][A_{[2,\omega )}][A_0\ast U_0][B_{[1,\omega )}][C_{[1,\omega )}]$
; since
![]() $\operatorname {\mathrm {Col}}(\nu ^+, \lambda )^V$
is
$\operatorname {\mathrm {Col}}(\nu ^+, \lambda )^V$
is
![]() $\nu ^+$
-closed in V, there is no obstacle to doing so.
$\nu ^+$
-closed in V, there is no obstacle to doing so.
The following claim is a strengthening of [Reference Neeman14, Lemma 5.8], and is why we require the auxiliary collapse
![]() $\operatorname {\mathrm {Col}}(\nu ^+, \lambda )^{V}$
. In order to have the small models contain all relevant objects, they need to be of size at least
$\operatorname {\mathrm {Col}}(\nu ^+, \lambda )^{V}$
. In order to have the small models contain all relevant objects, they need to be of size at least
![]() $|\lambda |$
; since we have collapsed
$|\lambda |$
; since we have collapsed
![]() $\lambda $
to
$\lambda $
to
![]() $\nu ^+$
, however, the
$\nu ^+$
, however, the
![]() $\nu ^+$
-closure of our posets is sufficient to obtain the desired generic.
$\nu ^+$
-closure of our posets is sufficient to obtain the desired generic.
Claim 3.30. Let R be a rank initial segment of the universe, large enough to contain all relevant objects. Let
![]() $\bar {M}[K] = \bar {V}[K][A_{[2,\omega )}][A_0\ast U_0][B_{[1,\omega )}][C_{[1,\omega )}]$
, where
$\bar {M}[K] = \bar {V}[K][A_{[2,\omega )}][A_0\ast U_0][B_{[1,\omega )}][C_{[1,\omega )}]$
, where
![]() $\bar {V}$
is the transitive collapse of
$\bar {V}$
is the transitive collapse of
![]() $X \prec R$
with
$X \prec R$
with
![]() $X \in V, V_\nu \subseteq X, |X| = \lambda $
,
$X \in V, V_\nu \subseteq X, |X| = \lambda $
,
![]() $\lambda \subseteq X$
, and X is closed under sequences of length
$\lambda \subseteq X$
, and X is closed under sequences of length
![]() $\nu $
in V. Let
$\nu $
in V. Let
![]() $\hat {A}_0$
be generic for
$\hat {A}_0$
be generic for
![]() $\operatorname {\mathrm {Add}}(\omega , (\nu ^{++})^{\bar {M}})$
over
$\operatorname {\mathrm {Add}}(\omega , (\nu ^{++})^{\bar {M}})$
over
![]() $M[K]\ (and\ also\ \bar {M}[K])$
. Let
$M[K]\ (and\ also\ \bar {M}[K])$
. Let
![]() $\pi :\bar {M}[K] \to \bar {M}^*[K^*]$
be the embedding from the previous claim applied in
$\pi :\bar {M}[K] \to \bar {M}^*[K^*]$
be the embedding from the previous claim applied in
![]() $\bar {M}[K][\hat {A}_0]$
. Let e be generic for
$\bar {M}[K][\hat {A}_0]$
. Let e be generic for
![]() $\operatorname {\mathrm {Col}}(\omega , \nu )$
over
$\operatorname {\mathrm {Col}}(\omega , \nu )$
over
![]() $M[K][\hat {A}_0]$
.
$M[K][\hat {A}_0]$
.
Then in
![]() $M[K][\hat {A}_0][e]$
there are filters
$M[K][\hat {A}_0][e]$
there are filters
![]() $A^*_1$
and
$A^*_1$
and
![]() $S^*_0$
so that
$S^*_0$
so that
![]() $A^*_1\times S^*_0\times e$
is generic for
$A^*_1\times S^*_0\times e$
is generic for
![]() $\pi (\mathbb {L})(\nu )$
over
$\pi (\mathbb {L})(\nu )$
over
![]() $\bar {M}^*[K^*]$
.
$\bar {M}^*[K^*]$
.
Proof As in [Reference Neeman14, Lemma 5.8], it is enough to find a generic
![]() $A_1^*\times C_0^*$
for the poset
$A_1^*\times C_0^*$
for the poset
![]() $\operatorname {\mathrm {Add}}(\nu ^+, \pi (\kappa _3))^{\bar {V}^*} \times \pi (\mathbb {C}_0)(\nu ^+)$
over
$\operatorname {\mathrm {Add}}(\nu ^+, \pi (\kappa _3))^{\bar {V}^*} \times \pi (\mathbb {C}_0)(\nu ^+)$
over
![]() $\bar {V}[K][A_{[2,\omega )}]$
that belongs to
$\bar {V}[K][A_{[2,\omega )}]$
that belongs to
![]() $V[K][A_{[2,\omega )}]$
. This can be done since
$V[K][A_{[2,\omega )}]$
. This can be done since
![]() $\operatorname {\mathrm {Add}}(\nu ^+, \pi (\kappa _3))^{\bar {V}^*} \times \pi (\mathbb {C}_0)(\nu ^+)$
is
$\operatorname {\mathrm {Add}}(\nu ^+, \pi (\kappa _3))^{\bar {V}^*} \times \pi (\mathbb {C}_0)(\nu ^+)$
is
![]() $\nu ^+$
-closed in
$\nu ^+$
-closed in
![]() $V[K][A_{[2,\omega )}]$
, and
$V[K][A_{[2,\omega )}]$
, and
![]() $\bar {V}[K][A_{2,\omega )}]$
has size
$\bar {V}[K][A_{2,\omega )}]$
has size
![]() $\nu ^+$
.
$\nu ^+$
.
Note that since
![]() $\lambda \subseteq X$
,
$\lambda \subseteq X$
,
![]() $\operatorname {\mathrm {Col}}(\nu ^+, \lambda )^V$
is in the transitive part of X, and thus is sent to itself by the transitive collapse.
$\operatorname {\mathrm {Col}}(\nu ^+, \lambda )^V$
is in the transitive part of X, and thus is sent to itself by the transitive collapse.
Claim 3.31. In
![]() $M[K]$
, for all
$M[K]$
, for all
![]() $m \geq 3$
, there is a generic
$m \geq 3$
, there is a generic
![]() $\nu ^+$
-supercompactness embedding with critical point
$\nu ^+$
-supercompactness embedding with critical point
![]() $\kappa _m$
. The poset adding this embedding is the product of
$\kappa _m$
. The poset adding this embedding is the product of
![]() $\operatorname {\mathrm {Add}}(\kappa _m, \pi (\kappa _{m+2}))^V$
,
$\operatorname {\mathrm {Add}}(\kappa _m, \pi (\kappa _{m+2}))^V$
,
![]() $\operatorname {\mathrm {Add}}(\kappa _{m+1}, \pi (\kappa _{m+3}))^V$
, and
$\operatorname {\mathrm {Add}}(\kappa _{m+1}, \pi (\kappa _{m+3}))^V$
, and
![]() $\pi (\mathbb {C})^{+F\upharpoonright \kappa _{m+2}}\upharpoonright (\kappa _{m+2}, \pi (\kappa _{m+2}))$
, where F is defined to be
$\pi (\mathbb {C})^{+F\upharpoonright \kappa _{m+2}}\upharpoonright (\kappa _{m+2}, \pi (\kappa _{m+2}))$
, where F is defined to be
![]() $A_0\ast U_0^{+B_{[1,\omega )}}.$
The full support
$A_0\ast U_0^{+B_{[1,\omega )}}.$
The full support
![]() $\kappa _{m}$
th power of this poset is
$\kappa _{m}$
th power of this poset is
![]() $<\kappa _m$
-distributive over
$<\kappa _m$
-distributive over
![]() $M[K]$
.
$M[K]$
.
Proof The proof is the argument of [Reference Neeman14, Lemma 5.6], carried out over
![]() $V[K]$
rather than V. Since K is generic for a
$V[K]$
rather than V. Since K is generic for a
![]() $\nu ^+$
-directed-closed poset, each
$\nu ^+$
-directed-closed poset, each
![]() $\kappa _n$
remains indestructibly supercompact in
$\kappa _n$
remains indestructibly supercompact in
![]() $V[K]$
, and all necessary properties of the other posets over V will still hold in
$V[K]$
, and all necessary properties of the other posets over V will still hold in
![]() $V[K]$
.
$V[K]$
.
Claim 3.32. There is
![]() $\mu \in \operatorname {\mathrm {Index}}$
so that in the extension of M by
$\mu \in \operatorname {\mathrm {Index}}$
so that in the extension of M by
![]() $\mathbb {L}_\mu $
, the strong tree property holds at
$\mathbb {L}_\mu $
, the strong tree property holds at
![]() $\nu ^+$
.
$\nu ^+$
.
Proof It suffices to check that the hypotheses of Theorem 3.14 hold for all
![]() $\lambda $
, with M serving as our ground model. First we note that
$\lambda $
, with M serving as our ground model. First we note that
![]() $M\models \kappa _n^+ = \kappa _{n+1}$
for all
$M\models \kappa _n^+ = \kappa _{n+1}$
for all
![]() ${n\geq 2}$
, and
${n\geq 2}$
, and
![]() $\mathbb {L}_\mu $
is
$\mathbb {L}_\mu $
is
![]() $\kappa _2$
-cc. The embedding for condition (1) is obtained from Claims 3.29 and 3.30, noting that for each
$\kappa _2$
-cc. The embedding for condition (1) is obtained from Claims 3.29 and 3.30, noting that for each
![]() $\lambda $
, the poset
$\lambda $
, the poset
![]() $\operatorname {\mathrm {Add}}(\omega , [\kappa _2, \pi (\kappa _2)))^V$
adding the embedding is the product of a
$\operatorname {\mathrm {Add}}(\omega , [\kappa _2, \pi (\kappa _2)))^V$
adding the embedding is the product of a
![]() $\nu ^+$
-Knaster poset and a
$\nu ^+$
-Knaster poset and a
![]() $\nu ^+$
-closed poset. The embeddings for condition (2) are obtained from Claim 3.31.
$\nu ^+$
-closed poset. The embeddings for condition (2) are obtained from Claim 3.31.
Let
![]() $\mu $
be given by the previous claim, and let
$\mu $
be given by the previous claim, and let
![]() $A_1 \times S_0 \times e$
be generic for
$A_1 \times S_0 \times e$
be generic for
![]() $\mathbb {L}_\mu $
over M. Let
$\mathbb {L}_\mu $
over M. Let
![]() $A = A_0\times A_1\times A_{[2,\omega )}$
. Let
$A = A_0\times A_1\times A_{[2,\omega )}$
. Let
![]() $U_{[1,\omega )}$
be the upwards closure of
$U_{[1,\omega )}$
be the upwards closure of
![]() $B_{[1,\omega )}$
in
$B_{[1,\omega )}$
in
![]() $\mathbb {U}_{[1,\omega )}$
, and let
$\mathbb {U}_{[1,\omega )}$
, and let
![]() $U = U_0 \times U_{[1,\omega )}$
. Let
$U = U_0 \times U_{[1,\omega )}$
. Let
![]() $S_{[1,\omega )}$
be the upwards closure of
$S_{[1,\omega )}$
be the upwards closure of
![]() $C_{[1,\omega )}$
in
$C_{[1,\omega )}$
in
![]() $\mathbb {C}^{+A\ast U}_{[1,\omega )}$
and let
$\mathbb {C}^{+A\ast U}_{[1,\omega )}$
and let
![]() $S = S_0 \ast S_{[1,\omega )}$
. Let N be the model
$S = S_0 \ast S_{[1,\omega )}$
. Let N be the model
![]() $V[A][U][S]$
.
$V[A][U][S]$
.
Proposition 3.33 [Reference Neeman14, Lemma 5.9].
There is a
![]() $\mu ^+$
-closed extension
$\mu ^+$
-closed extension
![]() $N[G]$
containing
$N[G]$
containing
![]() $M[A_1\times S_0]$
, with G still generic over
$M[A_1\times S_0]$
, with G still generic over
![]() $N[e]$
and both
$N[e]$
and both
![]() $\nu $
and
$\nu $
and
![]() $\nu ^+$
still cardinals in
$\nu ^+$
still cardinals in
![]() $N[e][G]$
.
$N[e][G]$
.
Proof The relevant model is the extension of N by the product of the factor forcing refining
![]() $U_{[1,\omega )}$
to a filter for
$U_{[1,\omega )}$
to a filter for
![]() $\mathbb {B}^{+A_0\ast \dot {\mathbb {U}}_0}\upharpoonright [\kappa _2,\nu )$
and the factor forcing refining
$\mathbb {B}^{+A_0\ast \dot {\mathbb {U}}_0}\upharpoonright [\kappa _2,\nu )$
and the factor forcing refining
![]() $S_{[1,\omega )}$
to a filter for
$S_{[1,\omega )}$
to a filter for
![]() $\mathbb {C}^{+A_0\ast \dot {\mathbb {U}}_0}\upharpoonright [\kappa _2,\nu )$
. By Facts 3.5 and 3.11, every descending sequence of conditions in these posets with length
$\mathbb {C}^{+A_0\ast \dot {\mathbb {U}}_0}\upharpoonright [\kappa _2,\nu )$
. By Facts 3.5 and 3.11, every descending sequence of conditions in these posets with length
![]() $<\kappa _2$
belonging to
$<\kappa _2$
belonging to
![]() $V[A_0\ast U_0]$
have lower bounds. From Fact 3.20 we see that every descending sequence of conditions in these posets with length less than
$V[A_0\ast U_0]$
have lower bounds. From Fact 3.20 we see that every descending sequence of conditions in these posets with length less than
![]() $\kappa _1 = \mu $
in
$\kappa _1 = \mu $
in
![]() $V[A][U][S]$
belong to
$V[A][U][S]$
belong to
![]() $V[A\upharpoonright \kappa _2][U\upharpoonright \kappa _1]$
, so they must belong to
$V[A\upharpoonright \kappa _2][U\upharpoonright \kappa _1]$
, so they must belong to
![]() $V[A_0\ast U_0]$
. We conclude that the factor posets are
$V[A_0\ast U_0]$
. We conclude that the factor posets are
![]() $\mu $
-closed in
$\mu $
-closed in
![]() $V[A][U][S]$
. When we extend
$V[A][U][S]$
. When we extend
![]() $N[e]$
by these posets, the resulting model is contained in
$N[e]$
by these posets, the resulting model is contained in
![]() $V[A][U\upharpoonright \kappa _1][B\upharpoonright [\kappa _1,\nu )][C][e]$
; this model preserves
$V[A][U\upharpoonright \kappa _1][B\upharpoonright [\kappa _1,\nu )][C][e]$
; this model preserves
![]() $\nu $
,
$\nu $
,
![]() $\nu ^+$
, and each
$\nu ^+$
, and each
![]() $\kappa _n$
. (For more details about the cardinal preservation, see [Reference Neeman14, Lemma 4.24] and [Reference Neeman14, Remark 4.25].)
$\kappa _n$
. (For more details about the cardinal preservation, see [Reference Neeman14, Lemma 4.24] and [Reference Neeman14, Remark 4.25].)
In particular,
![]() $N[G]$
projects to
$N[G]$
projects to
![]() $M[A_1\times S_0]$
, which projects to N. Moreover
$M[A_1\times S_0]$
, which projects to N. Moreover
![]() $M[\mathbb {L}_\mu ] = M[A_1\times S_0 \times e]$
, which projects to our final model
$M[\mathbb {L}_\mu ] = M[A_1\times S_0 \times e]$
, which projects to our final model
![]() $N[e]$
.
$N[e]$
.
Claim 3.34. In
![]() $N[e]$
, the strong tree property holds at
$N[e]$
, the strong tree property holds at
![]() $\nu ^+$
.
$\nu ^+$
.
Proof This is almost identical to the proof of [Reference Neeman14, Claim 6.5], using a slightly more general branch lemma. Let d be a thin
![]() $\mathcal {P}_{\nu ^+}(\lambda )$
-list. By Claim 3.32, d has a cofinal branch in the model
$\mathcal {P}_{\nu ^+}(\lambda )$
-list. By Claim 3.32, d has a cofinal branch in the model
![]() $M[A_1\times S_0 \times e]$
.
$M[A_1\times S_0 \times e]$
.
Let
![]() $N[G]$
be the extension of N given by Proposition 3.33. Since
$N[G]$
be the extension of N given by Proposition 3.33. Since
![]() $\dot {d}$
has a cofinal branch in
$\dot {d}$
has a cofinal branch in
![]() $M[A_1\times S_0\times e]$
, this branch is also present in
$M[A_1\times S_0\times e]$
, this branch is also present in
![]() $N[e][G]$
. Applying Lemmas 2.8 and 2.20, we conclude that the branch could not have been added by G. It follows that
$N[e][G]$
. Applying Lemmas 2.8 and 2.20, we conclude that the branch could not have been added by G. It follows that
![]() $\dot {d}$
has a cofinal branch in
$\dot {d}$
has a cofinal branch in
![]() $N[e]$
as desired.
$N[e]$
as desired.
Claim 3.35. In
![]() $N[e]$
, ITP holds at
$N[e]$
, ITP holds at
![]() $\aleph _{n}$
for all
$\aleph _{n}$
for all
![]() $n\geq 2$
.
$n\geq 2$
.
Proof This follows immediately from Theorem 3.17, noting that
![]() $\kappa _n = \aleph _n$
in
$\kappa _n = \aleph _n$
in
![]() $N[e]$
.
$N[e]$
.
We conclude that in
![]() $N[e]$
, ITP holds at
$N[e]$
, ITP holds at
![]() $\aleph _n$
for
$\aleph _n$
for
![]() $2 \leq n < w$
, and the strong tree property holds at
$2 \leq n < w$
, and the strong tree property holds at
![]() $\nu ^+ = \aleph _{\omega +1}$
. This completes the proof.
$\nu ^+ = \aleph _{\omega +1}$
. This completes the proof.
4. ITP at the successor of a singular cardinal
In this section, we give an analogue of Theorem 3.14, describing a general class of forcings which will obtain ITP at the successor of a singular cardinal. In particular, we show that ITP can be obtained at the successor of a singular cardinal with uncountable cofinality. Note that the hypotheses of this theorem are a little bit stricter; we impose more constraints on the structure of
![]() $\mathbb {L}_\mu $
, and we require
$\mathbb {L}_\mu $
, and we require
![]() $\kappa _0$
to be supercompact rather than merely generically supercompact. Our argument is a generalization of the techniques in [Reference Hachtman and Sinapova8].
$\kappa _0$
to be supercompact rather than merely generically supercompact. Our argument is a generalization of the techniques in [Reference Hachtman and Sinapova8].
As is becoming standard, we will prove the one-cardinal case separately for clarity.
4.1. The one-cardinal case
Theorem 4.1. Let
![]() $\tau $
be a regular cardinal. Let
$\tau $
be a regular cardinal. Let
![]() $\langle \kappa _\rho \mid \rho < \tau \rangle $
be an increasing continuous sequence of cardinals above
$\langle \kappa _\rho \mid \rho < \tau \rangle $
be an increasing continuous sequence of cardinals above
![]() $\tau $
with supremum
$\tau $
with supremum
![]() $\nu $
, such that
$\nu $
, such that
![]() $\kappa _{\rho }^+ = \kappa _{\rho +1}$
for all
$\kappa _{\rho }^+ = \kappa _{\rho +1}$
for all
![]() $\rho < \tau $
. Let
$\rho < \tau $
. Let
![]() $\operatorname {\mathrm {Index}}$
be a subset of
$\operatorname {\mathrm {Index}}$
be a subset of
![]() $\kappa _0$
, and fix
$\kappa _0$
, and fix
![]() $\rho ' < \tau $
. For each
$\rho ' < \tau $
. For each
![]() $\mu \in \operatorname {\mathrm {Index}}$
, let
$\mu \in \operatorname {\mathrm {Index}}$
, let
![]() $\mathbb {L}_\mu $
be the product of forcings
$\mathbb {L}_\mu $
be the product of forcings
![]() $\mathbb {P}_\mu $
and
$\mathbb {P}_\mu $
and
![]() $\mathbb {Q}_\mu $
where
$\mathbb {Q}_\mu $
where
![]() $|\mathbb {P}_\mu | < \mu ^+$
and
$|\mathbb {P}_\mu | < \mu ^+$
and
![]() $\mathbb {Q}_\mu $
is
$\mathbb {Q}_\mu $
is
![]() $\mu ^{++}$
-closed, such that
$\mu ^{++}$
-closed, such that
![]() $|\mathbb {L}_\mu | \leq \kappa _{\rho '}$
. In addition, suppose that we have the following
$|\mathbb {L}_\mu | \leq \kappa _{\rho '}$
. In addition, suppose that we have the following
![]() $:$
$:$
-
•
 $\kappa _0$
is
$\kappa _0$
is
 $\nu ^+$
-supercompact, with a normal measure
$\nu ^+$
-supercompact, with a normal measure
 $U_0$
on
$U_0$
on
 $\mathcal {P}_{\kappa _0}(\nu ^+)$
and corresponding embedding i, such that
$\mathcal {P}_{\kappa _0}(\nu ^+)$
and corresponding embedding i, such that
 $\nu \in i(\operatorname {\mathrm {Index}})$
.
$\nu \in i(\operatorname {\mathrm {Index}})$
. -
• For all ordinals
 $\rho < \tau $
there is a generic
$\rho < \tau $
there is a generic
 $\nu ^+$
-supercompactness embedding
$\nu ^+$
-supercompactness embedding
 $j_{\rho +2}$
with domain V and critical point
$j_{\rho +2}$
with domain V and critical point
 $\kappa _{\rho +2}$
, added by a poset
$\kappa _{\rho +2}$
, added by a poset
 $\mathbb {F}$
such that the full support power
$\mathbb {F}$
such that the full support power
 $\mathbb {P}^{\kappa _\rho }$
is
$\mathbb {P}^{\kappa _\rho }$
is
 $<\kappa _{\rho }$
-distributive in V.
$<\kappa _{\rho }$
-distributive in V.
Then there exists
![]() $\mu \in \operatorname {\mathrm {Index}}$
such that
$\mu \in \operatorname {\mathrm {Index}}$
such that
![]() $\operatorname {\mathrm {ITP}}(\nu ^+, \nu ^+)$
holds in the extension of V by
$\operatorname {\mathrm {ITP}}(\nu ^+, \nu ^+)$
holds in the extension of V by
![]() $\mathbb {L}_\mu $
.
$\mathbb {L}_\mu $
.
Proof Suppose not. For each
![]() $\mu \in \operatorname {\mathrm {Index}}$
, let
$\mu \in \operatorname {\mathrm {Index}}$
, let
![]() $\dot {d}^\mu $
be a
$\dot {d}^\mu $
be a
![]() $\mathbb {L}_\mu $
-name for a thin
$\mathbb {L}_\mu $
-name for a thin
![]() $\mathcal {P}_{\nu ^+}(\nu ^+)$
-list with no ineffable branch. Assume that the
$\mathcal {P}_{\nu ^+}(\nu ^+)$
-list with no ineffable branch. Assume that the
![]() $\alpha $
th level of
$\alpha $
th level of
![]() $\dot {d}^\mu $
is enumerated by the names
$\dot {d}^\mu $
is enumerated by the names
![]() $\{\dot {\sigma }_\alpha ^\mu (\xi ) \mid \xi < \nu \}$
, and that (for sufficiently large
$\{\dot {\sigma }_\alpha ^\mu (\xi ) \mid \xi < \nu \}$
, and that (for sufficiently large
![]() $\alpha $
) there are no repetitions in this sequence.
$\alpha $
) there are no repetitions in this sequence.
By assumption, we have a normal measure
![]() $U_0$
on
$U_0$
on
![]() $\mathcal {P}_{\kappa _0}(\nu ^+)$
, with corresponding embedding
$\mathcal {P}_{\kappa _0}(\nu ^+)$
, with corresponding embedding
![]() $i : V \to M$
. Let
$i : V \to M$
. Let
![]() $\kappa _x$
denote
$\kappa _x$
denote
![]() $\sup (\kappa _0 \cap x)$
. Recall that
$\sup (\kappa _0 \cap x)$
. Recall that
![]() $\kappa _x = \kappa _0 \cap x$
on a measure one set, and
$\kappa _x = \kappa _0 \cap x$
on a measure one set, and
![]() $[x \mapsto \kappa _x]_{U_0} = \kappa _0$
. Then
$[x \mapsto \kappa _x]_{U_0} = \kappa _0$
. Then
![]() $[x \mapsto \kappa _x^{+\tau }]_{U_0} = \kappa _0^{+\tau } = \nu $
. Let
$[x \mapsto \kappa _x^{+\tau }]_{U_0} = \kappa _0^{+\tau } = \nu $
. Let
![]() $\mu _x$
denote
$\mu _x$
denote
![]() $\kappa _x^{+\tau }$
. Note that since
$\kappa _x^{+\tau }$
. Note that since
![]() $\nu \in i(\operatorname {\mathrm {Index}})$
,
$\nu \in i(\operatorname {\mathrm {Index}})$
,
![]() $\mu _x \in \operatorname {\mathrm {Index}}$
on a measure one set. Note also that
$\mu _x \in \operatorname {\mathrm {Index}}$
on a measure one set. Note also that
![]() $i\dot {d}_{\sup i"\nu ^+}^{\nu } = [x \mapsto \dot {d}_{\sup x}^{\mu _x}]_{U_0}$
.
$i\dot {d}_{\sup i"\nu ^+}^{\nu } = [x \mapsto \dot {d}_{\sup x}^{\mu _x}]_{U_0}$
.
Lemma 4.2. There exists a successor ordinal
![]() $\rho $
with
$\rho $
with
![]() $\rho ' < \rho < \tau $
, an unbounded
$\rho ' < \rho < \tau $
, an unbounded
![]() $S \subseteq \nu ^+$
,
$S \subseteq \nu ^+$
,
![]() $A \in U_0$
, and a map
$A \in U_0$
, and a map
![]() $x \mapsto (p_x, q_x)$
such that for all
$x \mapsto (p_x, q_x)$
such that for all
![]() $x \in A$
and
$x \in A$
and
![]() $\alpha \in x\cap S$
, there is
$\alpha \in x\cap S$
, there is
![]() $\xi < \kappa _\rho $
such that
$\xi < \kappa _\rho $
such that
![]() $(p_x, q_x) \Vdash _{\mathbb {L}_{\mu _x}} \dot {d}_{\sup x}^{\mu _x} \cap \alpha = \dot {\sigma }^{\mu _x}_\alpha (\xi )$
.
$(p_x, q_x) \Vdash _{\mathbb {L}_{\mu _x}} \dot {d}_{\sup x}^{\mu _x} \cap \alpha = \dot {\sigma }^{\mu _x}_\alpha (\xi )$
.
Proof Let
![]() $\mathbb {L}$
denote
$\mathbb {L}$
denote
![]() $[x \mapsto \mathbb {L}_{\mu _x}]_{U_0}$
. By assumption, each
$[x \mapsto \mathbb {L}_{\mu _x}]_{U_0}$
. By assumption, each
![]() $\mathbb {L}_{\mu _x}$
is the product
$\mathbb {L}_{\mu _x}$
is the product
![]() $\mathbb {P}_{\mu _x} \times \mathbb {Q}_{\mu _x}$
, where
$\mathbb {P}_{\mu _x} \times \mathbb {Q}_{\mu _x}$
, where
![]() $|\mathbb {P}_{\mu _x}| < \mu _x^+$
and
$|\mathbb {P}_{\mu _x}| < \mu _x^+$
and
![]() $\mathbb {Q}_{\mu _x}$
is
$\mathbb {Q}_{\mu _x}$
is
![]() $\mu _x^{++}$
-closed. Let
$\mu _x^{++}$
-closed. Let
![]() $\mathbb {P} = [x \mapsto \mathbb {P}_{\mu _x}]_{U_0}$
and
$\mathbb {P} = [x \mapsto \mathbb {P}_{\mu _x}]_{U_0}$
and
![]() $\mathbb {Q} = [x\mapsto \mathbb {Q}_{\mu _x}]_{U_0}$
. We conclude that
$\mathbb {Q} = [x\mapsto \mathbb {Q}_{\mu _x}]_{U_0}$
. We conclude that
![]() $|\mathbb {P}| < \nu ^+$
,
$|\mathbb {P}| < \nu ^+$
,
![]() $\mathbb {Q}$
is
$\mathbb {Q}$
is
![]() $\nu ^{++}$
-closed, and
$\nu ^{++}$
-closed, and
![]() $\mathbb {L} = \mathbb {P} \times \mathbb {Q}$
.
$\mathbb {L} = \mathbb {P} \times \mathbb {Q}$
.
For all
![]() $\alpha < \nu ^+$
, there is some successor ordinal
$\alpha < \nu ^+$
, there is some successor ordinal
![]() $\rho _\alpha < \tau $
,
$\rho _\alpha < \tau $
,
![]() $\xi < i(\kappa _{\rho _\alpha })$
, and
$\xi < i(\kappa _{\rho _\alpha })$
, and
![]() $(p_\alpha , q_\alpha ) \in \mathbb {L}$
such that
$(p_\alpha , q_\alpha ) \in \mathbb {L}$
such that
![]() $(p_\alpha , q_\alpha ) \Vdash _{\mathbb {L}} i\dot {d}^{\nu }_{\sup i"\nu ^+}\cap i(\alpha ) = i\dot {\sigma }^{\nu }_{i(\alpha )}(\xi ).$
Since
$(p_\alpha , q_\alpha ) \Vdash _{\mathbb {L}} i\dot {d}^{\nu }_{\sup i"\nu ^+}\cap i(\alpha ) = i\dot {\sigma }^{\nu }_{i(\alpha )}(\xi ).$
Since
![]() $\mathbb {Q}$
is
$\mathbb {Q}$
is
![]() $\nu ^{++}$
-closed, working inductively we can choose the conditions
$\nu ^{++}$
-closed, working inductively we can choose the conditions
![]() $q_\alpha $
to be decreasing, with lower bound q. Since
$q_\alpha $
to be decreasing, with lower bound q. Since
![]() $|\mathbb {P}| < \nu ^+$
and
$|\mathbb {P}| < \nu ^+$
and
![]() $\tau < \nu ^+$
, there is an unbounded
$\tau < \nu ^+$
, there is an unbounded
![]() $S \subseteq \nu ^+$
, a fixed successor ordinal
$S \subseteq \nu ^+$
, a fixed successor ordinal
![]() $\rho < \tau $
, and a fixed
$\rho < \tau $
, and a fixed
![]() $p \in \mathbb {P}$
such that for all
$p \in \mathbb {P}$
such that for all
![]() $\alpha \in S$
,
$\alpha \in S$
,
![]() $\rho _\alpha = \rho $
and
$\rho _\alpha = \rho $
and
![]() $p_\alpha = p$
. Let
$p_\alpha = p$
. Let
![]() $[x \mapsto p_x]_{U_0} = p$
and
$[x \mapsto p_x]_{U_0} = p$
and
![]() $[x \mapsto q_x]_{U_0} = q$
.
$[x \mapsto q_x]_{U_0} = q$
.
Applying Łos’ theorem, we conclude that for all
![]() $\alpha \in S$
, there is a measure one set
$\alpha \in S$
, there is a measure one set
![]() $A_\alpha $
such that for all
$A_\alpha $
such that for all
![]() $x \in A_\alpha $
, there is
$x \in A_\alpha $
, there is
![]() $\xi < \kappa _\rho $
such that
$\xi < \kappa _\rho $
such that
![]() $(p_x, q_x) \Vdash _{\mathbb {L}_{\mu _x}} \dot {d}^{\mu _x}_{\sup x} \cap \alpha = \dot {\sigma }_\alpha ^{\mu _x}(\xi )$
. Let
$(p_x, q_x) \Vdash _{\mathbb {L}_{\mu _x}} \dot {d}^{\mu _x}_{\sup x} \cap \alpha = \dot {\sigma }_\alpha ^{\mu _x}(\xi )$
. Let
![]() $A \mathrel {\mathop :}= \triangle _{\alpha \in S} A_\alpha $
. This is a measure one set with the desired properties.
$A \mathrel {\mathop :}= \triangle _{\alpha \in S} A_\alpha $
. This is a measure one set with the desired properties.
Let
![]() $I = \{(\mu ,p,q) \mid \mu \in \operatorname {\mathrm {Index}}, (p,q) \in \mathbb {L}_\mu \}$
. For all
$I = \{(\mu ,p,q) \mid \mu \in \operatorname {\mathrm {Index}}, (p,q) \in \mathbb {L}_\mu \}$
. For all
![]() $s = (\mu ,p,q)$
in I, we define the relation
$s = (\mu ,p,q)$
in I, we define the relation
![]() $R_s$
on
$R_s$
on
![]() $S \times \kappa _\rho $
by
$S \times \kappa _\rho $
by
![]() $(\alpha , \zeta ) R_s (\beta , \xi )$
iff
$(\alpha , \zeta ) R_s (\beta , \xi )$
iff
![]() $\alpha \leq \beta $
and
$\alpha \leq \beta $
and
![]() $(p,q) \Vdash \dot {\sigma }^\mu _\alpha (\zeta ) = \dot {\sigma }_\beta ^\mu (\xi )\cap \alpha $
.
$(p,q) \Vdash \dot {\sigma }^\mu _\alpha (\zeta ) = \dot {\sigma }_\beta ^\mu (\xi )\cap \alpha $
.
Lemma 4.3.
![]() $\langle R_s \rangle _{s\in I}$
is a system on
$\langle R_s \rangle _{s\in I}$
is a system on
![]() $S \times \kappa _\rho $
.
$S \times \kappa _\rho $
.
Proof The first two conditions are trivial. For the third, let
![]() $\alpha < \beta $
both in S, and let
$\alpha < \beta $
both in S, and let
![]() $x \in A$
such that
$x \in A$
such that
![]() $\alpha , \beta \in x$
. Then there exist
$\alpha , \beta \in x$
. Then there exist
![]() $(p_x, q_x) \in \mathbb {L}_{\mu _x}$
and
$(p_x, q_x) \in \mathbb {L}_{\mu _x}$
and
![]() $\zeta , \xi < \kappa _\rho $
such that
$\zeta , \xi < \kappa _\rho $
such that
![]() $(p_x, q_x) \Vdash \dot {\sigma }_\alpha ^{\mu _x}(\zeta ) = \dot {\sigma }_\beta ^{\mu _x}(\xi )\cap \beta $
. In particular, letting
$(p_x, q_x) \Vdash \dot {\sigma }_\alpha ^{\mu _x}(\zeta ) = \dot {\sigma }_\beta ^{\mu _x}(\xi )\cap \beta $
. In particular, letting
![]() $s = (\mu _x, p_x, q_x)$
, we see that
$s = (\mu _x, p_x, q_x)$
, we see that
![]() $(\alpha , \zeta ) R_s (\beta , \xi )$
as desired.
$(\alpha , \zeta ) R_s (\beta , \xi )$
as desired.
Lemma 4.4. There exists an unbounded
![]() $S' \subseteq S$
and a system of branches
$S' \subseteq S$
and a system of branches
![]() $\langle b_{s,\delta } \mid s\in I, \delta < \kappa _\rho \rangle $
through
$\langle b_{s,\delta } \mid s\in I, \delta < \kappa _\rho \rangle $
through
![]() $\langle R_s \upharpoonright S'\times \kappa _\rho \rangle _{s\in I}$
such that each
$\langle R_s \upharpoonright S'\times \kappa _\rho \rangle _{s\in I}$
such that each
![]() $b_{s,\delta }$
is a branch through
$b_{s,\delta }$
is a branch through
![]() ${R_s\upharpoonright S'\times \kappa _\rho }$
.
${R_s\upharpoonright S'\times \kappa _\rho }$
.
Proof By assumption, we have a generic
![]() $\nu ^+$
-supercompactness embedding j with critical point
$\nu ^+$
-supercompactness embedding j with critical point
![]() $\kappa _{\rho +3}$
, added by a poset
$\kappa _{\rho +3}$
, added by a poset
![]() $\mathbb {F}$
with generic F whose full support power
$\mathbb {F}$
with generic F whose full support power
![]() $\mathbb {F}^{\kappa _{\rho +1}}$
is
$\mathbb {F}^{\kappa _{\rho +1}}$
is
![]() $<\kappa _{\rho +1}$
-distributive in V. Thus V satisfies hypothesis (2) of Lemma 2.22. Note that
$<\kappa _{\rho +1}$
-distributive in V. Thus V satisfies hypothesis (2) of Lemma 2.22. Note that
![]() $\mathbb {F}$
itself must also be
$\mathbb {F}$
itself must also be
![]() $<\kappa _{\rho +1}$
-distributive in V. Work in
$<\kappa _{\rho +1}$
-distributive in V. Work in
![]() $V[F]$
.
$V[F]$
.
Let
![]() $\gamma \in j(S) \setminus \sup j"\nu ^+$
. Note that each
$\gamma \in j(S) \setminus \sup j"\nu ^+$
. Note that each
![]() $\mathbb {L}_\mu $
has size
$\mathbb {L}_\mu $
has size
![]() $<\kappa _{\rho +3}$
. As before, we can assume that the underlying set of
$<\kappa _{\rho +3}$
. As before, we can assume that the underlying set of
![]() $\mathbb {L}_\mu $
is an ordinal, so that
$\mathbb {L}_\mu $
is an ordinal, so that
![]() $\mathbb {L}_\mu $
is a bounded subset of
$\mathbb {L}_\mu $
is a bounded subset of
![]() $V_{\kappa _{\rho +3}}$
; it follows that
$V_{\kappa _{\rho +3}}$
; it follows that
![]() $j(I) = I$
. For each
$j(I) = I$
. For each
![]() $\delta < \kappa _\rho $
and
$\delta < \kappa _\rho $
and
![]() $s = (\mu , p,q) \in I,$
we define
$s = (\mu , p,q) \in I,$
we define
We claim that
![]() $\langle b_{s,\delta } \mid s\in I, \delta < \kappa _\rho \rangle $
is a system of branches through
$\langle b_{s,\delta } \mid s\in I, \delta < \kappa _\rho \rangle $
is a system of branches through
![]() $\langle R_s\rangle _{s\in I}$
. By construction, each
$\langle R_s\rangle _{s\in I}$
. By construction, each
![]() $b_{s,\delta }$
is linearly ordered and downwards closed. It remains to verify that
$b_{s,\delta }$
is linearly ordered and downwards closed. It remains to verify that
![]() $\bigcup \operatorname {\mathrm {dom}}(b_{s,\delta }) = S$
.
$\bigcup \operatorname {\mathrm {dom}}(b_{s,\delta }) = S$
.
Since
![]() $\kappa _\rho < \operatorname {\mathrm {crit}}(j)$
, we can apply elementarity to Lemma 4.2, concluding that for all
$\kappa _\rho < \operatorname {\mathrm {crit}}(j)$
, we can apply elementarity to Lemma 4.2, concluding that for all
![]() $\alpha \in S$
and
$\alpha \in S$
and
![]() $x \in j(A)$
with
$x \in j(A)$
with
![]() $j(\alpha ), \gamma $
both in x, there exist
$j(\alpha ), \gamma $
both in x, there exist
![]() $\zeta , \delta < \kappa _\rho $
and
$\zeta , \delta < \kappa _\rho $
and
![]() ${s = (\mu _x, p_x, q_x) \in j(I) = I}$
such that
${s = (\mu _x, p_x, q_x) \in j(I) = I}$
such that
In particular,
![]() $\bigcup \operatorname {\mathrm {dom}}(b_{s,\delta }) = S$
. This system may not belong to V, since it is defined in
$\bigcup \operatorname {\mathrm {dom}}(b_{s,\delta }) = S$
. This system may not belong to V, since it is defined in
![]() $V[F]$
, but it satisfies condition (1) of Lemma 2.22. Applying that lemma, we conclude that there is some
$V[F]$
, but it satisfies condition (1) of Lemma 2.22. Applying that lemma, we conclude that there is some
![]() $(s, \delta ) \in I \times \kappa _{\rho }$
such that
$(s, \delta ) \in I \times \kappa _{\rho }$
such that
![]() $b_{s,\delta }$
is cofinal and belongs to V.
$b_{s,\delta }$
is cofinal and belongs to V.
Let
![]() $\mathcal {D} = \{(s, \delta )\mid b_{s,\delta }\in V\}$
. Since
$\mathcal {D} = \{(s, \delta )\mid b_{s,\delta }\in V\}$
. Since
![]() $\mathbb {F}$
is
$\mathbb {F}$
is
![]() $<\kappa _{\rho +1}$
-distributive,
$<\kappa _{\rho +1}$
-distributive,
![]() $\mathcal {D} \in V$
, and in fact
$\mathcal {D} \in V$
, and in fact
![]() $\langle b_{s,\delta } \mid (s,\delta ) \in \mathcal {D}\rangle $
is also in V. Since
$\langle b_{s,\delta } \mid (s,\delta ) \in \mathcal {D}\rangle $
is also in V. Since
![]() $\mathcal {D}$
must contain at least one pair
$\mathcal {D}$
must contain at least one pair
![]() $(s,\delta )$
corresponding to a cofinal branch, the set
$(s,\delta )$
corresponding to a cofinal branch, the set
![]() $S' = \bigcup _{(s,\delta ) \in \mathcal {D}} \operatorname {\mathrm {dom}}(b_{s,\delta })$
is unbounded in
$S' = \bigcup _{(s,\delta ) \in \mathcal {D}} \operatorname {\mathrm {dom}}(b_{s,\delta })$
is unbounded in
![]() $\nu ^+$
, and
$\nu ^+$
, and
![]() $\langle b_{s,\delta }\rangle _{(s,\delta )\in \mathcal {D}}$
is a system of branches through
$\langle b_{s,\delta }\rangle _{(s,\delta )\in \mathcal {D}}$
is a system of branches through
![]() $\langle R_s \upharpoonright S' \times \kappa _\rho \rangle _{s\in I}$
.
$\langle R_s \upharpoonright S' \times \kappa _\rho \rangle _{s\in I}$
.
In addition, by taking a subset of
![]() $I \times \kappa _\rho $
if needed, we may assume that for all
$I \times \kappa _\rho $
if needed, we may assume that for all
![]() $s \in I$
and
$s \in I$
and
![]() $\eta < \delta < \kappa _\rho $
, if
$\eta < \delta < \kappa _\rho $
, if
![]() $b_{s,\eta }$
and
$b_{s,\eta }$
and
![]() $b_{s,\delta }$
are both cofinal, then they are distinct. In particular, we can assume that if
$b_{s,\delta }$
are both cofinal, then they are distinct. In particular, we can assume that if
![]() $b_{s,\delta }$
and
$b_{s,\delta }$
and
![]() $b_{s,\eta }$
are (defined and) equal cofinally often, then
$b_{s,\eta }$
are (defined and) equal cofinally often, then
![]() $\delta = \eta $
. We can do this by removing any duplicates, which may appear if
$\delta = \eta $
. We can do this by removing any duplicates, which may appear if
![]() $j\dot {\sigma }_\gamma ^\mu (\eta )$
and
$j\dot {\sigma }_\gamma ^\mu (\eta )$
and
![]() $j\dot \sigma _\gamma ^\mu (\delta )$
are above
$j\dot \sigma _\gamma ^\mu (\delta )$
are above
![]() $\sup j"\nu ^+$
. (Note that by the distributivity of
$\sup j"\nu ^+$
. (Note that by the distributivity of
![]() $\mathbb {F}$
, the necessary subset of
$\mathbb {F}$
, the necessary subset of
![]() $I \times \kappa _\rho $
will still be in V.)
$I \times \kappa _\rho $
will still be in V.)
For all
![]() $(s, \delta ) \in \mathcal {D}$
, we define
$(s, \delta ) \in \mathcal {D}$
, we define
![]() $\dot {\pi }_{s,\delta } = \bigcup \{\dot {\sigma }_\alpha ^\mu (\zeta ) \mid (\alpha , \zeta ) \in b_{s,\delta }\}$
. As in [Reference Hachtman and Sinapova8], these branches have some useful properties. Let
$\dot {\pi }_{s,\delta } = \bigcup \{\dot {\sigma }_\alpha ^\mu (\zeta ) \mid (\alpha , \zeta ) \in b_{s,\delta }\}$
. As in [Reference Hachtman and Sinapova8], these branches have some useful properties. Let
![]() $s = (\mu ,p,q)$
and
$s = (\mu ,p,q)$
and
![]() $s' = (\mu , p', q')$
. If
$s' = (\mu , p', q')$
. If
![]() $(p',q')\leq (p,q)$
, then
$(p',q')\leq (p,q)$
, then
![]() $R_s \subseteq R_{s'}$
, and
$R_s \subseteq R_{s'}$
, and
![]() $b_{s,\delta } \subseteq b_{s',\delta }$
for all
$b_{s,\delta } \subseteq b_{s',\delta }$
for all
![]() $\delta < \kappa _\rho $
. Moreover, if
$\delta < \kappa _\rho $
. Moreover, if
![]() $b_{s,\delta }$
is cofinal and
$b_{s,\delta }$
is cofinal and
![]() $(s,\delta )\in \mathcal {D}$
, then
$(s,\delta )\in \mathcal {D}$
, then
![]() $(s', \delta ) \in \mathcal {D}$
. If
$(s', \delta ) \in \mathcal {D}$
. If
![]() $b_{s,\delta }$
is cofinal, then
$b_{s,\delta }$
is cofinal, then
![]() $(p,q)$
forces that
$(p,q)$
forces that
![]() $\dot {\pi }_{s,\delta }$
is a cofinal branch through
$\dot {\pi }_{s,\delta }$
is a cofinal branch through
![]() $\dot {d}^\mu $
.
$\dot {d}^\mu $
.
Next, we wish to bound the splitting for all branches (including those not in V). Working in
![]() $V[F]$
, for each
$V[F]$
, for each
![]() $\eta < \delta < \kappa _\rho $
and
$\eta < \delta < \kappa _\rho $
and
![]() $s\in I$
, we define
$s\in I$
, we define
![]() $\alpha _{s,\eta ,\delta }$
as follows. If
$\alpha _{s,\eta ,\delta }$
as follows. If
![]() $b_{s,\delta }$
and
$b_{s,\delta }$
and
![]() $b_{s,\eta }$
are both bounded, we define
$b_{s,\eta }$
are both bounded, we define
![]() $\alpha _{s,\eta ,\delta }$
to be
$\alpha _{s,\eta ,\delta }$
to be
![]() $\sup \left (\operatorname {\mathrm {dom}}(b_{s,\eta }) \cup \operatorname {\mathrm {dom}}(b_{s,\delta })\right )$
. If not, then we define
$\sup \left (\operatorname {\mathrm {dom}}(b_{s,\eta }) \cup \operatorname {\mathrm {dom}}(b_{s,\delta })\right )$
. If not, then we define
![]() $\alpha _{s,\eta ,\delta }$
to be the least
$\alpha _{s,\eta ,\delta }$
to be the least
![]() $\alpha $
such that for all
$\alpha $
such that for all
![]() $\alpha '> \alpha $
,
$\alpha '> \alpha $
,
![]() $b_{s,\eta }(\alpha ')$
and
$b_{s,\eta }(\alpha ')$
and
![]() $b_{s,\delta }(\alpha ')$
are not both defined and equal. Note that each
$b_{s,\delta }(\alpha ')$
are not both defined and equal. Note that each
![]() $\alpha _{s,\eta ,\delta }$
is below
$\alpha _{s,\eta ,\delta }$
is below
![]() $\nu ^+$
; if it isn’t, then
$\nu ^+$
; if it isn’t, then
![]() $b_{s,\eta ,\delta }$
must agree on cofinally many
$b_{s,\eta ,\delta }$
must agree on cofinally many
![]() $\alpha $
, but since we have removed duplicate branches this would mean that
$\alpha $
, but since we have removed duplicate branches this would mean that
![]() $\delta = \eta $
.
$\delta = \eta $
.
Let
![]() $\bar {\alpha } = \sup _{s\in I,\eta <\delta <\kappa _\rho } \alpha _{s,\eta ,\delta }+1$
. Then if
$\bar {\alpha } = \sup _{s\in I,\eta <\delta <\kappa _\rho } \alpha _{s,\eta ,\delta }+1$
. Then if
![]() $\alpha> \bar {\alpha }$
and
$\alpha> \bar {\alpha }$
and
![]() $b_{s,\delta }(\alpha ) = b_{s,\eta }(\alpha )$
,
$b_{s,\delta }(\alpha ) = b_{s,\eta }(\alpha )$
,
![]() $\delta = \eta $
and
$\delta = \eta $
and
![]() $b_{s,\delta }$
is cofinal.
$b_{s,\delta }$
is cofinal.
For all
![]() $x \in A$
, let
$x \in A$
, let
![]() $(p_x, q_x) \in \mathbb {L}_{\mu _x}$
be as in Lemma 4.2. Define
$(p_x, q_x) \in \mathbb {L}_{\mu _x}$
be as in Lemma 4.2. Define
![]() $s_x = (\mu _x, p_x, q_x)$
.
$s_x = (\mu _x, p_x, q_x)$
.
Lemma 4.5. There exists an unbounded
![]() $\bar {S}\subseteq S'$
and
$\bar {S}\subseteq S'$
and
![]() $\bar {A}\in U_0$
with
$\bar {A}\in U_0$
with
![]() $\bar {A} \subseteq A$
such that for all
$\bar {A} \subseteq A$
such that for all
![]() $x \in \bar {A}$
and all
$x \in \bar {A}$
and all
![]() $\alpha \in \bar {S}\cap x$
, the following statement holds
$\alpha \in \bar {S}\cap x$
, the following statement holds
![]() $:$
$:$
Proof Define
![]() $A_\alpha \mathrel {\mathop :}= \{x\in A \mid (\dagger _{x,\alpha }) \text { holds }\}$
. It suffices to show that
$A_\alpha \mathrel {\mathop :}= \{x\in A \mid (\dagger _{x,\alpha }) \text { holds }\}$
. It suffices to show that
![]() $\bar {S} = \{\alpha \in S' \mid A_\alpha \in U_0\}$
is unbounded in
$\bar {S} = \{\alpha \in S' \mid A_\alpha \in U_0\}$
is unbounded in
![]() $\mu $
; if this holds, then
$\mu $
; if this holds, then
![]() $\bar {A} = A \cap \triangle _{\alpha \in \bar {S}} A_\alpha $
will have the desired properties.
$\bar {A} = A \cap \triangle _{\alpha \in \bar {S}} A_\alpha $
will have the desired properties.
Suppose
![]() $\bar {S}$
is bounded. Fix
$\bar {S}$
is bounded. Fix
![]() $\alpha _0 < \nu ^+$
such that
$\alpha _0 < \nu ^+$
such that
![]() $\bar {\alpha } < \alpha _0$
and
$\bar {\alpha } < \alpha _0$
and
![]() $A_\alpha \notin U_0$
for all
$A_\alpha \notin U_0$
for all
![]() $\alpha> \alpha _0$
that are in
$\alpha> \alpha _0$
that are in
![]() $S'$
. Define
$S'$
. Define
![]() $A' \mathrel {\mathop :}= A \cap \triangle _{\alpha _0 < \alpha \in S'} \mathcal {P}_{\kappa _0}(\nu ^+)\setminus A_\alpha $
. Then
$A' \mathrel {\mathop :}= A \cap \triangle _{\alpha _0 < \alpha \in S'} \mathcal {P}_{\kappa _0}(\nu ^+)\setminus A_\alpha $
. Then
![]() $A' \in U_0$
, and
$A' \in U_0$
, and
![]() $\dagger _{x,\alpha }$
fails whenever
$\dagger _{x,\alpha }$
fails whenever
![]() $\alpha _0 < \alpha $
,
$\alpha _0 < \alpha $
,
![]() $\alpha \in x\cap S'$
, and
$\alpha \in x\cap S'$
, and
![]() $x \in A'$
.
$x \in A'$
.
Let
![]() $R^{\prime }_s$
be obtained by removing every ground model branch from
$R^{\prime }_s$
be obtained by removing every ground model branch from
![]() $R_s$
. That is, for each
$R_s$
. That is, for each
![]() $s\in I$
,
$s\in I$
,
![]() $(\alpha , \zeta ) R^{\prime }_s (\beta , \xi )$
if and only if
$(\alpha , \zeta ) R^{\prime }_s (\beta , \xi )$
if and only if
![]() $\alpha _0 < \alpha ,\beta \in S', (\alpha , \zeta ) R_s (\beta , \xi )$
, and for all
$\alpha _0 < \alpha ,\beta \in S', (\alpha , \zeta ) R_s (\beta , \xi )$
, and for all
![]() $\delta < \kappa _\rho $
, if
$\delta < \kappa _\rho $
, if
![]() $(s,\delta ) \in \mathcal {D}$
, then
$(s,\delta ) \in \mathcal {D}$
, then
![]() $(\alpha , \zeta ) \notin b_{s,\delta }$
. We wish to show that
$(\alpha , \zeta ) \notin b_{s,\delta }$
. We wish to show that
![]() $\langle R^{\prime }_s\rangle _{s \in I}$
is a system on
$\langle R^{\prime }_s\rangle _{s \in I}$
is a system on
![]() $(S' \setminus \alpha _0)\times \kappa _\rho $
.
$(S' \setminus \alpha _0)\times \kappa _\rho $
.
As before, the first two conditions are immediate from the definition. For the third, suppose
![]() $\alpha _0<\alpha <\beta $
with
$\alpha _0<\alpha <\beta $
with
![]() $\alpha , \beta $
both in
$\alpha , \beta $
both in
![]() $S'$
. We need to show that there exists
$S'$
. We need to show that there exists
![]() $\zeta , \xi < \kappa _{\rho }$
and
$\zeta , \xi < \kappa _{\rho }$
and
![]() $s \in I$
such that
$s \in I$
such that
![]() $(\alpha , \zeta ) R^{\prime }_s (\beta , \xi )$
. Let
$(\alpha , \zeta ) R^{\prime }_s (\beta , \xi )$
. Let
![]() $\gamma \in j(S) \setminus \sup j"\nu ^+$
be the element used in the previous lemma to define the system of branches. Note that
$\gamma \in j(S) \setminus \sup j"\nu ^+$
be the element used in the previous lemma to define the system of branches. Note that
![]() $\{x \mid j(\alpha ), j(\beta ), \gamma \in x\}$
is a club in
$\{x \mid j(\alpha ), j(\beta ), \gamma \in x\}$
is a club in
![]() $\mathcal {P}_{\kappa _0}(j(\nu ^+))$
. Since
$\mathcal {P}_{\kappa _0}(j(\nu ^+))$
. Since
![]() $A'$
intersects every club in
$A'$
intersects every club in
![]() $\mathcal {P}_{\kappa _0}(\nu ^+)$
, by elementarity we conclude that there exists some
$\mathcal {P}_{\kappa _0}(\nu ^+)$
, by elementarity we conclude that there exists some
![]() $x' \in j(A')$
with
$x' \in j(A')$
with
![]() $j(\alpha ), j(\beta )$
, and
$j(\alpha ), j(\beta )$
, and
![]() $\gamma $
all in
$\gamma $
all in
![]() $x'$
. Note that
$x'$
. Note that
![]() $j(\alpha ), j(\beta ) \in j(S)$
. Applying elementarity to Lemma 4.2, we conclude that there exist
$j(\alpha ), j(\beta ) \in j(S)$
. Applying elementarity to Lemma 4.2, we conclude that there exist
![]() $\zeta , \xi , \delta < \kappa _\rho $
such that
$\zeta , \xi , \delta < \kappa _\rho $
such that
and each of these are forced by
![]() $(p_{x'}, q_{x'})$
to cohere with
$(p_{x'}, q_{x'})$
to cohere with
![]() $\dot {j}d_{\sup x}^{\mu _x}$
. Note that
$\dot {j}d_{\sup x}^{\mu _x}$
. Note that
![]() $x'$
may not be the image of an element from the ground model. Since
$x'$
may not be the image of an element from the ground model. Since
![]() $s_{x'} \in j(I) = I$
, however, by elementarity there exists
$s_{x'} \in j(I) = I$
, however, by elementarity there exists
![]() $x\in A'$
with
$x\in A'$
with
![]() $\alpha , \beta \in x$
such that
$\alpha , \beta \in x$
such that
![]() $s_x = s_{x'}$
. We conclude that
$s_x = s_{x'}$
. We conclude that
![]() $(\alpha , \zeta )$
and
$(\alpha , \zeta )$
and
![]() $(\beta , \xi )$
are both in
$(\beta , \xi )$
are both in
![]() $b_{s_{x'},\delta }$
, with
$b_{s_{x'},\delta }$
, with
![]() $(\alpha , \zeta ) R_{s_{x'}} (\beta , \xi )$
.
$(\alpha , \zeta ) R_{s_{x'}} (\beta , \xi )$
.
Since we are above the splitting, if
![]() $(\alpha , \zeta ) \in b_{s_x,\delta '}$
for any
$(\alpha , \zeta ) \in b_{s_x,\delta '}$
for any
![]() $\delta ' \neq \delta $
, this branch must coincide with
$\delta ' \neq \delta $
, this branch must coincide with
![]() $b_{s_x, \delta }$
. So to finish showing that
$b_{s_x, \delta }$
. So to finish showing that
![]() $(\alpha , \zeta ) R^{\prime }_{s_x} (\beta , \xi )$
, we simply need to show that
$(\alpha , \zeta ) R^{\prime }_{s_x} (\beta , \xi )$
, we simply need to show that
![]() $(s_x, \delta ) \notin \mathcal {D}$
. We will do this by contradiction.
$(s_x, \delta ) \notin \mathcal {D}$
. We will do this by contradiction.
Suppose
![]() $(s_x, \delta ) \in \mathcal {D}$
. Since
$(s_x, \delta ) \in \mathcal {D}$
. Since
![]() $\alpha _0 <\alpha $
and
$\alpha _0 <\alpha $
and
![]() $\alpha \in x\cap S'$
with
$\alpha \in x\cap S'$
with
![]() $x \in A'$
,
$x \in A'$
,
![]() $(\dagger _{x,\alpha })$
must fail. Then
$(\dagger _{x,\alpha })$
must fail. Then
We have chosen x so that
But since
![]() $(\alpha , \zeta ) \in b_{s_x,\delta }$
, by the definition of
$(\alpha , \zeta ) \in b_{s_x,\delta }$
, by the definition of
![]() $\pi _{s_x,\delta }$
we must have
$\pi _{s_x,\delta }$
we must have
This gives a contradiction. It follows that
![]() $(s_x, \delta ) \notin \mathcal {D}$
, concluding our proof that
$(s_x, \delta ) \notin \mathcal {D}$
, concluding our proof that
![]() $\langle R^{\prime }_s\rangle _{s\in I}$
is a system.
$\langle R^{\prime }_s\rangle _{s\in I}$
is a system.
For each
![]() $(s,\delta ) \notin \mathcal {D}$
, let
$(s,\delta ) \notin \mathcal {D}$
, let
![]() $b^{\prime }_{s,\delta }$
be the restriction of
$b^{\prime }_{s,\delta }$
be the restriction of
![]() $b_{s,\delta }$
to
$b_{s,\delta }$
to
![]() $R^{\prime }_s$
. Then
$R^{\prime }_s$
. Then
![]() $\langle b^{\prime }_{s,\delta } \mid (s,\delta ) \notin \mathcal {D}\rangle $
is a system of branches through
$\langle b^{\prime }_{s,\delta } \mid (s,\delta ) \notin \mathcal {D}\rangle $
is a system of branches through
![]() $\langle R^{\prime }_s\rangle _{s \in I}$
. Repeating the argument of Lemma 4.4, we conclude that there exists some
$\langle R^{\prime }_s\rangle _{s \in I}$
. Repeating the argument of Lemma 4.4, we conclude that there exists some
![]() $s \in I$
and
$s \in I$
and
![]() $\delta < \kappa _\rho $
such that
$\delta < \kappa _\rho $
such that
![]() $b^{\prime }_{s,\delta } \upharpoonright R_s'$
is cofinal and belongs to V. Since we can recover
$b^{\prime }_{s,\delta } \upharpoonright R_s'$
is cofinal and belongs to V. Since we can recover
![]() $b_{s,\delta }$
from any cofinal subset, we conclude that
$b_{s,\delta }$
from any cofinal subset, we conclude that
![]() $(s,\delta )$
must be in
$(s,\delta )$
must be in
![]() $\mathcal {D}$
, contradicting our definition of
$\mathcal {D}$
, contradicting our definition of
![]() $R_s'$
. This contradiction proves our initial claim that
$R_s'$
. This contradiction proves our initial claim that
![]() $\bar {S}$
is unbounded; thus we can construct
$\bar {S}$
is unbounded; thus we can construct
![]() $\bar {A}$
with the desired properties as described above.
$\bar {A}$
with the desired properties as described above.
Let
![]() $S^* = \bar {S} \setminus (\bar {\alpha }+1)$
; this set is still unbounded. Let
$S^* = \bar {S} \setminus (\bar {\alpha }+1)$
; this set is still unbounded. Let
![]() $A^* = \{x \in A \mid x \cap S^* \text { cofinal in } \sup x\}$
, noting that
$A^* = \{x \in A \mid x \cap S^* \text { cofinal in } \sup x\}$
, noting that
![]() $A^* \in U_0$
. For all
$A^* \in U_0$
. For all
![]() $x \in A^*$
and
$x \in A^*$
and
![]() $\alpha \in x\cap S^*$
, the witness
$\alpha \in x\cap S^*$
, the witness
![]() $\delta $
to
$\delta $
to
![]() $(\dagger _{x,\alpha })$
depends only on x: if we have
$(\dagger _{x,\alpha })$
depends only on x: if we have
![]() $\alpha < \beta $
both in
$\alpha < \beta $
both in
![]() $S^*$
and
$S^*$
and
![]() $\delta , \delta ' < \kappa _n$
, where
$\delta , \delta ' < \kappa _n$
, where
![]() $(p_x,q_x) \Vdash \dot {d}^{\mu _x}_{\sup x}\cap \alpha = \dot {\pi }_{s_x, \delta }\cap \alpha $
and
$(p_x,q_x) \Vdash \dot {d}^{\mu _x}_{\sup x}\cap \alpha = \dot {\pi }_{s_x, \delta }\cap \alpha $
and
![]() $(p_x,q_x) \Vdash \dot {d}^{\mu _x}_{\sup x}\cap \beta = \dot {\pi }_{s_x, \delta '}\cap \beta $
, then clearly
$(p_x,q_x) \Vdash \dot {d}^{\mu _x}_{\sup x}\cap \beta = \dot {\pi }_{s_x, \delta '}\cap \beta $
, then clearly
![]() $(p_x,q_x) \Vdash \dot {\pi }_{s_x, \delta }\cap \alpha = \dot {\pi }_{s_x, \delta '}\cap \alpha $
. Since the branches are forced to cohere up to
$(p_x,q_x) \Vdash \dot {\pi }_{s_x, \delta }\cap \alpha = \dot {\pi }_{s_x, \delta '}\cap \alpha $
. Since the branches are forced to cohere up to
![]() $\alpha $
, and
$\alpha $
, and
![]() $\alpha $
is above the splitting, then
$\alpha $
is above the splitting, then
![]() $(p_x, q_x)$
must force them to be equal; since we have removed duplicate branches, it follows that
$(p_x, q_x)$
must force them to be equal; since we have removed duplicate branches, it follows that
![]() $\delta = \delta '$
.
$\delta = \delta '$
.
Since the witness
![]() $\delta $
depends only on x, we see that for all
$\delta $
depends only on x, we see that for all
![]() $\alpha \in S^*\cap x$
,
$\alpha \in S^*\cap x$
,
![]() $(p_x, q_x) \Vdash \dot {d}_{\sup x}^{\mu _x}\cap \alpha = \dot {\pi }_{s_x, \delta }\cap \alpha $
. We conclude that
$(p_x, q_x) \Vdash \dot {d}_{\sup x}^{\mu _x}\cap \alpha = \dot {\pi }_{s_x, \delta }\cap \alpha $
. We conclude that
![]() $(p_x, q_x) \Vdash \dot {d}_{\sup x}^{\mu _x} = \dot {\pi }_{s_x, \delta }\cap \sup x.$
$(p_x, q_x) \Vdash \dot {d}_{\sup x}^{\mu _x} = \dot {\pi }_{s_x, \delta }\cap \sup x.$
For each
![]() $s = (\mu ,p,q)$
and
$s = (\mu ,p,q)$
and
![]() $\delta $
such that
$\delta $
such that
![]() $(s,\delta ) \in \mathcal {D}$
, we define
$(s,\delta ) \in \mathcal {D}$
, we define
![]() $T_{s,\delta } = \{\alpha < \nu ^+ \mid (p,q) \Vdash _{\mathbb {L}_{\mu }} \dot {d}^{\mu }_\alpha = \dot {\pi }_{s,\delta }\cap \alpha \}$
. Let
$T_{s,\delta } = \{\alpha < \nu ^+ \mid (p,q) \Vdash _{\mathbb {L}_{\mu }} \dot {d}^{\mu }_\alpha = \dot {\pi }_{s,\delta }\cap \alpha \}$
. Let
![]() $T = \bigcup _{(s,\delta ) \in \mathcal {D}} T_{s,\delta }$
. We have shown that
$T = \bigcup _{(s,\delta ) \in \mathcal {D}} T_{s,\delta }$
. We have shown that
![]() $\{\sup x \mid x \in A^*\} \subseteq T$
, so T must be stationary. Since
$\{\sup x \mid x \in A^*\} \subseteq T$
, so T must be stationary. Since
![]() $|\mathcal {D}| \leq \kappa _\rho < \nu ^+$
, there must be some fixed
$|\mathcal {D}| \leq \kappa _\rho < \nu ^+$
, there must be some fixed
![]() $(s,\delta )$
such that
$(s,\delta )$
such that
![]() $T_{s,\delta }$
is stationary. Since
$T_{s,\delta }$
is stationary. Since
![]() $\mathbb {L}_\mu $
has the
$\mathbb {L}_\mu $
has the
![]() $\nu ^+$
-cc, it will preserve stationary subsets of
$\nu ^+$
-cc, it will preserve stationary subsets of
![]() $\nu ^+$
. We conclude that
$\nu ^+$
. We conclude that
![]() $b_{s,\delta }$
defines an ineffable branch through
$b_{s,\delta }$
defines an ineffable branch through
![]() $\dot {d}^\mu $
in any generic extension of V by
$\dot {d}^\mu $
in any generic extension of V by
![]() $\mathbb {L}_\mu $
containing
$\mathbb {L}_\mu $
containing
![]() $(p,q)$
.
$(p,q)$
.
4.2. The two-cardinal case
Theorem 4.6. Let
![]() $\tau $
be a regular cardinal. Let
$\tau $
be a regular cardinal. Let
![]() $\langle \kappa _\rho \mid \rho < \tau \rangle $
be an increasing continuous sequence of cardinals above
$\langle \kappa _\rho \mid \rho < \tau \rangle $
be an increasing continuous sequence of cardinals above
![]() $\tau $
with supremum
$\tau $
with supremum
![]() $\nu $
, such that
$\nu $
, such that
![]() $\kappa _{\rho }^+ = \kappa _{\rho +1}$
for all
$\kappa _{\rho }^+ = \kappa _{\rho +1}$
for all
![]() $\rho < \tau $
. Let
$\rho < \tau $
. Let
![]() $\operatorname {\mathrm {Index}}$
be a subset of
$\operatorname {\mathrm {Index}}$
be a subset of
![]() $\kappa _0$
such that every
$\kappa _0$
such that every
![]() $\mu \in \operatorname {\mathrm {Index}}$
has cofinality
$\mu \in \operatorname {\mathrm {Index}}$
has cofinality
![]() $\tau $
. For each
$\tau $
. For each
![]() $\mu \in \operatorname {\mathrm {Index}}$
, let
$\mu \in \operatorname {\mathrm {Index}}$
, let
![]() $\mathbb {L}_\mu $
be the product of forcings
$\mathbb {L}_\mu $
be the product of forcings
![]() $\mathbb {P}_\mu $
and
$\mathbb {P}_\mu $
and
![]() $\mathbb {Q}_\mu $
, where
$\mathbb {Q}_\mu $
, where
![]() $|\mathbb {P}_\mu | < \mu ^+$
and
$|\mathbb {P}_\mu | < \mu ^+$
and
![]() $\mathbb {Q}_\mu $
is
$\mathbb {Q}_\mu $
is
![]() $\mu ^{++}$
-closed, such that
$\mu ^{++}$
-closed, such that
![]() $|\mathbb {L}_\mu | < \kappa _{\rho '}$
for some fixed
$|\mathbb {L}_\mu | < \kappa _{\rho '}$
for some fixed
![]() $\rho ' < \tau $
. In addition, suppose that we have the following
$\rho ' < \tau $
. In addition, suppose that we have the following
![]() $:$
$:$
-
•
 $\kappa _0$
is indestructibly
$\kappa _0$
is indestructibly
 $\nu ^+$
-supercompact, with a normal measure
$\nu ^+$
-supercompact, with a normal measure
 $U_0$
on
$U_0$
on
 $\mathcal {P}_{\kappa _0}(\nu ^+)$
and corresponding embedding i such that
$\mathcal {P}_{\kappa _0}(\nu ^+)$
and corresponding embedding i such that
 $\nu \in i(\operatorname {\mathrm {Index}})$
.
$\nu \in i(\operatorname {\mathrm {Index}})$
. -
• For all ordinals
 $\rho < \tau $
and all
$\rho < \tau $
and all
 $\lambda \geq \nu ^+$
, there is a generic
$\lambda \geq \nu ^+$
, there is a generic
 $\lambda $
-supercompactness embedding
$\lambda $
-supercompactness embedding
 $j_{\rho +2}$
with domain V and critical point
$j_{\rho +2}$
with domain V and critical point
 $\kappa _{\rho +2}$
, added by a poset
$\kappa _{\rho +2}$
, added by a poset
 $\mathbb {F}$
such that the full support power
$\mathbb {F}$
such that the full support power
 $\mathbb {F}^{\kappa _\rho }$
is
$\mathbb {F}^{\kappa _\rho }$
is
 $<\kappa _{\rho }$
-distributive in V.
$<\kappa _{\rho }$
-distributive in V.
Then there exists
![]() $\mu \in \operatorname {\mathrm {Index}}$
such that
$\mu \in \operatorname {\mathrm {Index}}$
such that
![]() $\operatorname {\mathrm {ITP}}$
holds at
$\operatorname {\mathrm {ITP}}$
holds at
![]() $\nu ^+$
in the extension of V by
$\nu ^+$
in the extension of V by
![]() $\mathbb {L}_\mu $
.
$\mathbb {L}_\mu $
.
Proof As before, let
![]() $\kappa $
denote
$\kappa $
denote
![]() $\kappa _0$
. Suppose the theorem fails. Then for every
$\kappa _0$
. Suppose the theorem fails. Then for every
![]() $\mu < \kappa $
, there is some
$\mu < \kappa $
, there is some
![]() $\lambda $
such that
$\lambda $
such that
![]() $\operatorname {\mathrm {ITP}}(\nu ^+, \lambda )$
fails in the extension by
$\operatorname {\mathrm {ITP}}(\nu ^+, \lambda )$
fails in the extension by
![]() $\mathbb {L}_\mu $
. By taking a supremum, we can assume that
$\mathbb {L}_\mu $
. By taking a supremum, we can assume that
![]() $\lambda $
is the same for all
$\lambda $
is the same for all
![]() $\mu $
, and that
$\mu $
, and that
![]() $\lambda ^{\nu ^+} = \lambda $
. For each
$\lambda ^{\nu ^+} = \lambda $
. For each
![]() $\mu \in \operatorname {\mathrm {Index}}$
, let
$\mu \in \operatorname {\mathrm {Index}}$
, let
![]() $\dot {d}^\mu $
be a name for a thin
$\dot {d}^\mu $
be a name for a thin
![]() $\mathcal {P}_{\nu ^+}(\lambda )$
list which is forced by
$\mathcal {P}_{\nu ^+}(\lambda )$
list which is forced by
![]() $1_{\mathbb {L}_\mu }$
not to have an ineffable branch. Let K be generic for
$1_{\mathbb {L}_\mu }$
not to have an ineffable branch. Let K be generic for
![]() $\operatorname {\mathrm {Col}}(\nu ^+, \lambda )^{V}$
over V. Note that in
$\operatorname {\mathrm {Col}}(\nu ^+, \lambda )^{V}$
over V. Note that in
![]() $V[K]$
,
$V[K]$
,
![]() $\lambda $
is no longer a cardinal, since it has been collapsed; it is simply a set with size
$\lambda $
is no longer a cardinal, since it has been collapsed; it is simply a set with size
![]() $\nu ^+$
. Since we can assume that
$\nu ^+$
. Since we can assume that
![]() $\lambda $
was regular in V, we can likewise assume that
$\lambda $
was regular in V, we can likewise assume that
![]() $\lambda $
has cofinality
$\lambda $
has cofinality
![]() $\nu ^+$
in
$\nu ^+$
in
![]() $V[K]$
. It is still meaningful to discuss ineffable branches through thin
$V[K]$
. It is still meaningful to discuss ineffable branches through thin
![]() $\mathcal {P}_{\nu ^+}(\lambda )$
lists when
$\mathcal {P}_{\nu ^+}(\lambda )$
lists when
![]() $\lambda $
is a set rather than a cardinal.
$\lambda $
is a set rather than a cardinal.
Theorem 4.7. There is
![]() $\mu \in \operatorname {\mathrm {Index}}$
such that in
$\mu \in \operatorname {\mathrm {Index}}$
such that in
![]() $V[K][\mathbb {L}_\mu ]$
,
$V[K][\mathbb {L}_\mu ]$
,
![]() $d^\mu $
has an ineffable branch.
$d^\mu $
has an ineffable branch.
Assuming this theorem, we will complete the proof of Theorem 4.6. Let b be an ineffable branch for
![]() $d^\mu $
in
$d^\mu $
in
![]() $V[K][\mathbb {L}_\mu ]$
. Since
$V[K][\mathbb {L}_\mu ]$
. Since
![]() $\operatorname {\mathrm {Col}}(\nu ^+, \lambda )$
is
$\operatorname {\mathrm {Col}}(\nu ^+, \lambda )$
is
![]() $\nu ^+$
-closed in V, and
$\nu ^+$
-closed in V, and
![]() $\mathbb {L}_\mu $
is
$\mathbb {L}_\mu $
is
![]() $\kappa _\rho $
-cc for some
$\kappa _\rho $
-cc for some
![]() $\rho < \tau $
, we conclude by Lemma 2.20 that
$\rho < \tau $
, we conclude by Lemma 2.20 that
![]() $\operatorname {\mathrm {Col}}(\nu ^+, \lambda )$
is forced to have the thin
$\operatorname {\mathrm {Col}}(\nu ^+, \lambda )$
is forced to have the thin
![]() $\nu ^+$
-approximation property. Therefore
$\nu ^+$
-approximation property. Therefore
![]() $b \in V[\mathbb {L}_\mu ]$
. Since stationarity is downwards absolute, b is an ineffable branch for
$b \in V[\mathbb {L}_\mu ]$
. Since stationarity is downwards absolute, b is an ineffable branch for
![]() $d^\mu $
in
$d^\mu $
in
![]() $V[\mathbb {L}_\mu ]$
, contradicting our assumption.
$V[\mathbb {L}_\mu ]$
, contradicting our assumption.
We will now prove Theorem 4.7. Note that in
![]() $V[K]$
,
$V[K]$
,
![]() $\lambda $
is no longer a cardinal, having been collapsed to have cardinality and cofinality
$\lambda $
is no longer a cardinal, having been collapsed to have cardinality and cofinality
![]() $\nu ^+$
. Since
$\nu ^+$
. Since
![]() $\lambda $
has cardinality and cofinality
$\lambda $
has cardinality and cofinality
![]() $\nu ^+$
,
$\nu ^+$
,
![]() $\mathcal {P}_{\nu ^+}(\lambda )$
is order-isomorphic to
$\mathcal {P}_{\nu ^+}(\lambda )$
is order-isomorphic to
![]() $\mathcal {P}_{\nu ^+}(\nu ^+)$
. Using this isomorphism, we can identify our thin
$\mathcal {P}_{\nu ^+}(\nu ^+)$
. Using this isomorphism, we can identify our thin
![]() $\mathcal {P}_{\nu ^+}(\lambda )$
-list with a thin
$\mathcal {P}_{\nu ^+}(\lambda )$
-list with a thin
![]() $\mathcal {P}_{\nu ^+}(\nu ^+)$
-list; an ineffable branch in one will correspond to an ineffable branch in the other.
$\mathcal {P}_{\nu ^+}(\nu ^+)$
-list; an ineffable branch in one will correspond to an ineffable branch in the other.
To finish the proof, it suffices to verify the assumptions of Theorem 4.1 in
![]() $V[K]$
. Since
$V[K]$
. Since
![]() $\operatorname {\mathrm {Col}}(\nu ^+, \lambda )$
is
$\operatorname {\mathrm {Col}}(\nu ^+, \lambda )$
is
![]() $\nu ^+$
-closed, each
$\nu ^+$
-closed, each
![]() $\mathbb {L}_\mu $
remains the product of a small and a closed forcing. Since
$\mathbb {L}_\mu $
remains the product of a small and a closed forcing. Since
![]() $\kappa _0$
is indestructibly supercompact in V, it will remain supercompact in
$\kappa _0$
is indestructibly supercompact in V, it will remain supercompact in
![]() $V[K]$
.
$V[K]$
.
By assumption, for each
![]() $\rho < \tau $
, there is a generic
$\rho < \tau $
, there is a generic
![]() $\lambda $
-supercompactness embedding
$\lambda $
-supercompactness embedding
![]() $j_{\rho +2}$
with domain V and critical point
$j_{\rho +2}$
with domain V and critical point
![]() $\kappa _{\rho +2}$
, added by a poset
$\kappa _{\rho +2}$
, added by a poset
![]() $\mathbb {F}$
whose
$\mathbb {F}$
whose
![]() $\kappa _\rho $
-power is
$\kappa _\rho $
-power is
![]() ${<\kappa _\rho }$
-distributive in V. We wish to extend the domain of
${<\kappa _\rho }$
-distributive in V. We wish to extend the domain of
![]() $j_{\rho +2}$
to
$j_{\rho +2}$
to
![]() $V[K]$
. Note that
$V[K]$
. Note that
![]() $\bigcup j"K$
is a condition in
$\bigcup j"K$
is a condition in
![]() $j(\operatorname {\mathrm {Col}}(\nu ^+,\lambda )^{V[K]}) = \operatorname {\mathrm {Col}}(j(\nu ^+, j(\lambda ))^{V[K]})$
, so the embedding will be contained in
$j(\operatorname {\mathrm {Col}}(\nu ^+,\lambda )^{V[K]}) = \operatorname {\mathrm {Col}}(j(\nu ^+, j(\lambda ))^{V[K]})$
, so the embedding will be contained in
![]() $V[K][F][K^*]$
, where F is generic for
$V[K][F][K^*]$
, where F is generic for
![]() $\mathbb {F}$
and
$\mathbb {F}$
and
![]() $K^*$
is a generic for
$K^*$
is a generic for
![]() $\operatorname {\mathrm {Col}}(j(\nu ^+), j(\lambda ))^{V[K]}$
containing
$\operatorname {\mathrm {Col}}(j(\nu ^+), j(\lambda ))^{V[K]}$
containing
![]() $\bigcup j"K$
. Noting that
$\bigcup j"K$
. Noting that
![]() $\mathbb {F}\times \operatorname {\mathrm {Col}}(j(\nu ^+), j(\lambda ))^{V[K]}$
will have a
$\mathbb {F}\times \operatorname {\mathrm {Col}}(j(\nu ^+), j(\lambda ))^{V[K]}$
will have a
![]() $<\kappa _{\rho }$
-distributive
$<\kappa _{\rho }$
-distributive
![]() $\kappa _\rho $
-power, it follows that the second condition of Theorem 4.1 holds. We conclude that there is
$\kappa _\rho $
-power, it follows that the second condition of Theorem 4.1 holds. We conclude that there is
![]() $\mu \in \operatorname {\mathrm {Index}}$
such that in
$\mu \in \operatorname {\mathrm {Index}}$
such that in
![]() $V[K][\mathbb {L}_\mu ]$
,
$V[K][\mathbb {L}_\mu ]$
,
![]() $d^\mu $
has an ineffable branch. This concludes the proof.
$d^\mu $
has an ineffable branch. This concludes the proof.
Corollary 4.8. Let
![]() $\tau $
be a regular cardinal with
$\tau $
be a regular cardinal with
![]() $\tau < \aleph _\tau $
, and let
$\tau < \aleph _\tau $
, and let
![]() $\langle \kappa _\rho \mid \rho < \tau \rangle $
be a continuous increasing sequence of cardinals with supremum
$\langle \kappa _\rho \mid \rho < \tau \rangle $
be a continuous increasing sequence of cardinals with supremum
![]() $\nu $
such that the following holds
$\nu $
such that the following holds
![]() $:$
$:$
-
•
 $\kappa _{\rho +1} = \kappa _{\rho }^+$
for all limit ordinals
$\kappa _{\rho +1} = \kappa _{\rho }^+$
for all limit ordinals
 $\rho < \tau .$
$\rho < \tau .$
-
•
 $\kappa _n$
is indestructibly supercompact for all
$\kappa _n$
is indestructibly supercompact for all
 $n < \omega .$
$n < \omega .$
-
•
 $\kappa _{\rho +2}$
is indestructibly supercompact for all
$\kappa _{\rho +2}$
is indestructibly supercompact for all
 $\omega \leq \rho < \tau .$
$\omega \leq \rho < \tau .$
Then there is a generic extension in which ITP holds at
![]() $\aleph _{\tau +1}$
, and
$\aleph _{\tau +1}$
, and
![]() $\tau $
remains a regular cardinal.
$\tau $
remains a regular cardinal.
Proof Define
 $$\begin{align*}\mathbb{H} = \left(\prod _{\rho < \omega} \operatorname{\mathrm{Col}}(\kappa_\rho, <\kappa_{\rho+1})\right)\times \left(\prod_{\omega\leq \rho < \tau }\operatorname{\mathrm{Col}}(\kappa_{\rho+1}, <\kappa_{\rho+2})\right),\end{align*}$$
$$\begin{align*}\mathbb{H} = \left(\prod _{\rho < \omega} \operatorname{\mathrm{Col}}(\kappa_\rho, <\kappa_{\rho+1})\right)\times \left(\prod_{\omega\leq \rho < \tau }\operatorname{\mathrm{Col}}(\kappa_{\rho+1}, <\kappa_{\rho+2})\right),\end{align*}$$
and let H be generic for
![]() $\mathbb {H}$
. Let
$\mathbb {H}$
. Let
![]() $\operatorname {\mathrm {Index}}$
be the set of all
$\operatorname {\mathrm {Index}}$
be the set of all
![]() $\mu < \kappa _0$
of cofinality
$\mu < \kappa _0$
of cofinality
![]() $\tau $
. For all
$\tau $
. For all
![]() $\mu \in \operatorname {\mathrm {Index}}$
, let
$\mu \in \operatorname {\mathrm {Index}}$
, let
![]() $\mathbb {L}_{\mu } = \operatorname {\mathrm {Col}}(\tau , \mu ) \times \operatorname {\mathrm {Col}}(\mu ^{++}, <\kappa _0)$
.
$\mathbb {L}_{\mu } = \operatorname {\mathrm {Col}}(\tau , \mu ) \times \operatorname {\mathrm {Col}}(\mu ^{++}, <\kappa _0)$
.
We apply Theorem 4.6 to
![]() $V[H]$
to obtain
$V[H]$
to obtain
![]() $\mu \in \operatorname {\mathrm {Index}}$
such that in the extension of
$\mu \in \operatorname {\mathrm {Index}}$
such that in the extension of
![]() $V[H]$
by
$V[H]$
by
![]() $\mathbb {L}_\mu $
, ITP holds at
$\mathbb {L}_\mu $
, ITP holds at
![]() $\nu ^+$
. In this extension,
$\nu ^+$
. In this extension,
![]() $\kappa _{\rho +1} = \kappa _{\rho }^+$
for all
$\kappa _{\rho +1} = \kappa _{\rho }^+$
for all
![]() $\rho < \tau $
, while
$\rho < \tau $
, while
![]() $\kappa _0$
becomes
$\kappa _0$
becomes
![]() $\tau ^{+3}$
, so
$\tau ^{+3}$
, so
![]() $\nu = \aleph _\tau $
and
$\nu = \aleph _\tau $
and
![]() $\nu ^+ = \aleph _{\tau +1}$
. Note also that since every poset is either
$\nu ^+ = \aleph _{\tau +1}$
. Note also that since every poset is either
![]() $\tau $
-cc or
$\tau $
-cc or
![]() $\tau $
-closed,
$\tau $
-closed,
![]() $\tau $
remains a regular cardinal.
$\tau $
remains a regular cardinal.
5. ITP from
 $\aleph _4$
to
$\aleph _4$
to
 $\aleph _{\omega +1}$
$\aleph _{\omega +1}$
When we attempt to apply the results of the previous section to Neeman’s construction, we run into several issues: in particular,
![]() $\mathbb {L}_{\mu }$
will not be sufficiently closed, and Theorem 4.6 doesn’t work when i is a generic embedding. We can avoid these issues by making the following modifications:
$\mathbb {L}_{\mu }$
will not be sufficiently closed, and Theorem 4.6 doesn’t work when i is a generic embedding. We can avoid these issues by making the following modifications:
-
• We index our list of supercompact cardinals starting at
 $3$
rather than
$3$
rather than
 $2$
. Our choice of
$2$
. Our choice of
 $\mu \in \operatorname {\mathrm {Index}}$
will select not only
$\mu \in \operatorname {\mathrm {Index}}$
will select not only
 $\kappa _1 \mathrel {\mathop :}= \mu ^+$
but also
$\kappa _1 \mathrel {\mathop :}= \mu ^+$
but also
 $\kappa _2 \mathrel {\mathop :}= \mu ^{++}$
.
$\kappa _2 \mathrel {\mathop :}= \mu ^{++}$
. -
• We replace
 $\mathbb {A}_0$
and
$\mathbb {A}_0$
and
 $\mathbb {A}_1$
with the trivial forcings.
$\mathbb {A}_1$
with the trivial forcings. -
• We replace
 $\mathbb {C}_0$
with the trivial poset, since we do not need any collapses to obtain
$\mathbb {C}_0$
with the trivial poset, since we do not need any collapses to obtain
 $\kappa _1^+ = \kappa _2$
.
$\kappa _1^+ = \kappa _2$
. -
• Since
 $\mathbb {A}_0$
and
$\mathbb {A}_0$
and
 $\mathbb {A}_1$
are trivial, we can remove most of the restrictions on
$\mathbb {A}_1$
are trivial, we can remove most of the restrictions on
 $\operatorname {\mathrm {Index}}$
.
$\operatorname {\mathrm {Index}}$
. -
• Since
 $\mathbb {A}_1$
is trivial, the poset
$\mathbb {A}_1$
is trivial, the poset
 $\mathbb {C}_1$
will not collapse cardinals between
$\mathbb {C}_1$
will not collapse cardinals between
 $\kappa _2$
and
$\kappa _2$
and
 $\kappa _3$
, so we replace it with the trivial poset. We add
$\kappa _3$
, so we replace it with the trivial poset. We add
 $\operatorname {\mathrm {Col}}(\kappa _2, <\kappa _3)$
to the product. Note that this poset depends on the parameter
$\operatorname {\mathrm {Col}}(\kappa _2, <\kappa _3)$
to the product. Note that this poset depends on the parameter
 $\kappa _2 = \mu ^{++}$
.
$\kappa _2 = \mu ^{++}$
. -
• Since
 $\mathbb {A}_0, \mathbb {A}_1$
,
$\mathbb {A}_0, \mathbb {A}_1$
,
 $\mathbb {C}_0$
, and
$\mathbb {C}_0$
, and
 $\mathbb {C}_1$
are all trivial, we do not require the initial stages of Laver preparation, so we can set
$\mathbb {C}_1$
are all trivial, we do not require the initial stages of Laver preparation, so we can set
 $\mathbb {U}_0, \mathbb {B}_0, \mathbb {U}_1$
, and
$\mathbb {U}_0, \mathbb {B}_0, \mathbb {U}_1$
, and
 $\mathbb {B}_1$
to likewise be trivial.
$\mathbb {B}_1$
to likewise be trivial. -
• We replace
 $\mathbb {A}_2$
with
$\mathbb {A}_2$
with
 $\sum _{\mu \in \operatorname {\mathrm {Index}}} \operatorname {\mathrm {Add}}(\mu ^{++}, \kappa _4)$
.
$\sum _{\mu \in \operatorname {\mathrm {Index}}} \operatorname {\mathrm {Add}}(\mu ^{++}, \kappa _4)$
.
Note that
![]() $\kappa _2$
will no longer be generically supercompact, so the tree property (and thus also ITP) will not hold at
$\kappa _2$
will no longer be generically supercompact, so the tree property (and thus also ITP) will not hold at
![]() $\aleph _2$
in the final model. Note also that since we removed
$\aleph _2$
in the final model. Note also that since we removed
![]() $\mathbb {A}_1$
, GCH will hold at
$\mathbb {A}_1$
, GCH will hold at
![]() $\aleph _1$
, so the tree property will also fail at
$\aleph _1$
, so the tree property will also fail at
![]() $\aleph _3$
.
$\aleph _3$
.
We now formally define the construction. Let
![]() $\langle \kappa _n \mid 3 \leq n < \omega \rangle $
be an increasing sequence of indestructibly supercompact cardinals with supremum
$\langle \kappa _n \mid 3 \leq n < \omega \rangle $
be an increasing sequence of indestructibly supercompact cardinals with supremum
![]() $\nu $
, and suppose there is a partial function
$\nu $
, and suppose there is a partial function
![]() $\phi $
such that for all n,
$\phi $
such that for all n,
![]() $\phi \upharpoonright \kappa _n$
is an indestructible Laver function for
$\phi \upharpoonright \kappa _n$
is an indestructible Laver function for
![]() $\kappa _n$
and for all
$\kappa _n$
and for all
![]() $\alpha \in \operatorname {\mathrm {dom}}(\phi )$
, if
$\alpha \in \operatorname {\mathrm {dom}}(\phi )$
, if
![]() $\gamma $
is in
$\gamma $
is in
![]() $\operatorname {\mathrm {dom}}(\phi )\cap \alpha $
then
$\operatorname {\mathrm {dom}}(\phi )\cap \alpha $
then
![]() $\phi (\gamma ) \in V_\alpha $
.
$\phi (\gamma ) \in V_\alpha $
.
Definition 5.1. We define the set Index as the set of all
![]() $\mu < \kappa _3$
so that
$\mu < \kappa _3$
so that
![]() $\mu $
is a strong limit cardinal of cofinality
$\mu $
is a strong limit cardinal of cofinality
![]() $\omega $
and
$\omega $
and
![]() $\operatorname {\mathrm {dom}}(\phi )$
has a largest point
$\operatorname {\mathrm {dom}}(\phi )$
has a largest point
![]() $\lambda $
below
$\lambda $
below
![]() $\mu $
.
$\mu $
.
Note that the elements of
![]() $\{\mu ^+ \mid \mu \in \operatorname {\mathrm {Index}} \}$
are the potential options for
$\{\mu ^+ \mid \mu \in \operatorname {\mathrm {Index}} \}$
are the potential options for
![]() $\aleph _1$
, and
$\aleph _1$
, and
![]() $\{\mu ^{++} \mid \mu \in \operatorname {\mathrm {Index}}\}$
are the potential options for
$\{\mu ^{++} \mid \mu \in \operatorname {\mathrm {Index}}\}$
are the potential options for
![]() $\aleph _2$
. (Unlike in Section 3, we can define this set in advance because
$\aleph _2$
. (Unlike in Section 3, we can define this set in advance because
![]() $A_0$
and
$A_0$
and
![]() $A_1$
are trivial, so Index won’t depend on them.)
$A_1$
are trivial, so Index won’t depend on them.)
Definition 5.2. For
![]() $n \geq 3$
, let
$n \geq 3$
, let
![]() $\mathbb {A}_n \mathrel {\mathop :}= \operatorname {\mathrm {Add}}(\kappa _n, \kappa _{n+2})$
. Let
$\mathbb {A}_n \mathrel {\mathop :}= \operatorname {\mathrm {Add}}(\kappa _n, \kappa _{n+2})$
. Let
![]() $\kappa _0$
denote
$\kappa _0$
denote
![]() $\omega $
, and set
$\omega $
, and set
![]() $\mathbb {A}_0$
and
$\mathbb {A}_0$
and
![]() $\mathbb {A}_1$
to be the trivial forcings. Let
$\mathbb {A}_1$
to be the trivial forcings. Let
![]() $A_2 = \sum _{\mu \in \text {Index}} \operatorname {\mathrm {Add}}(\mu ^{++}, \kappa _4)$
. We use
$A_2 = \sum _{\mu \in \text {Index}} \operatorname {\mathrm {Add}}(\mu ^{++}, \kappa _4)$
. We use
![]() $\kappa _1$
and
$\kappa _1$
and
![]() $\kappa _2$
to refer to the values
$\kappa _2$
to refer to the values
![]() $\mu ^+$
and
$\mu ^+$
and
![]() $\mu ^{++}$
chosen by a fixed generic. Let
$\mu ^{++}$
chosen by a fixed generic. Let
![]() $\mathbb {A}$
be the full support product of
$\mathbb {A}$
be the full support product of
![]() $\mathbb {A}_n$
for
$\mathbb {A}_n$
for
![]() $n < \omega $
.
$n < \omega $
.
The Laver preparation posets
![]() $\mathbb {B}$
and
$\mathbb {B}$
and
![]() $\mathbb {U}$
are constructed exactly as in Definition 3.2, except that we define
$\mathbb {U}$
are constructed exactly as in Definition 3.2, except that we define
![]() $\mathbb {B}_0$
,
$\mathbb {B}_0$
,
![]() $\mathbb {B}_1$
,
$\mathbb {B}_1$
,
![]() $\mathbb {U}_0$
, and
$\mathbb {U}_0$
, and
![]() $\mathbb {U}_1$
to be trivial. Since
$\mathbb {U}_1$
to be trivial. Since
![]() $\mathbb {A}_0$
and
$\mathbb {A}_0$
and
![]() $\mathbb {A}_1$
are trivial, and we won’t be using
$\mathbb {A}_1$
are trivial, and we won’t be using
![]() $\mathbb {C}$
to collapse cardinals below
$\mathbb {C}$
to collapse cardinals below
![]() $\kappa _3$
, we do not need any Laver preparation for those cardinals. The collapsing poset
$\kappa _3$
, we do not need any Laver preparation for those cardinals. The collapsing poset
![]() $\mathbb {C}_n$
is as defined in Definition 3.8, except that we define
$\mathbb {C}_n$
is as defined in Definition 3.8, except that we define
![]() $\mathbb {C}_0$
and
$\mathbb {C}_0$
and
![]() $\mathbb {C}_1$
to be trivial.
$\mathbb {C}_1$
to be trivial.
Let A be generic for
![]() $\mathbb {A}$
, U be generic for
$\mathbb {A}$
, U be generic for
![]() $\mathbb {U}$
over
$\mathbb {U}$
over
![]() $V[A]$
, S be generic for
$V[A]$
, S be generic for
![]() $\mathbb {C}^{+A\ast U}$
over
$\mathbb {C}^{+A\ast U}$
over
![]() $V[A][U]$
, and e be generic for
$V[A][U]$
, and e be generic for
![]() $\operatorname {\mathrm {Col}}(\omega , \mu )\times \operatorname {\mathrm {Col}}(\mu ^{++}, <\kappa _3)$
over
$\operatorname {\mathrm {Col}}(\omega , \mu )\times \operatorname {\mathrm {Col}}(\mu ^{++}, <\kappa _3)$
over
![]() $V[A][U][S]$
, noting that
$V[A][U][S]$
, noting that
![]() $\mu $
is determined by the generic for
$\mu $
is determined by the generic for
![]() $\mathbb {A}_2$
included in A.
$\mathbb {A}_2$
included in A.
The cardinal structure in
![]() $V[A][U][S][e]$
is similar to that in Neeman’s construction.
$V[A][U][S][e]$
is similar to that in Neeman’s construction.
Claim 5.3. In
![]() $V[A][U][S][e]$
, the following properties hold.
$V[A][U][S][e]$
, the following properties hold.
-
•
 $\kappa _n = \aleph _n$
for each n.
$\kappa _n = \aleph _n$
for each n. -
•
 $2^{\kappa _n} = \kappa _{n+2}$
for each
$2^{\kappa _n} = \kappa _{n+2}$
for each
 $n> 1$
.
$n> 1$
.
Proof Clearly
![]() $\kappa _1 = \aleph _1$
, and
$\kappa _1 = \aleph _1$
, and
![]() $\kappa _2 = \kappa _1^+$
in V. To verify that
$\kappa _2 = \kappa _1^+$
in V. To verify that
![]() $\kappa _2 = \aleph _2$
, we need only check that
$\kappa _2 = \aleph _2$
, we need only check that
![]() $\kappa _2$
is not collapsed. This follows from [Reference Neeman14, Claims 4.18–4.21]. Similarly, the cardinals between
$\kappa _2$
is not collapsed. This follows from [Reference Neeman14, Claims 4.18–4.21]. Similarly, the cardinals between
![]() $\kappa _2$
and
$\kappa _2$
and
![]() $\kappa _3$
are collapsed, while
$\kappa _3$
are collapsed, while
![]() $\kappa _3$
is preserved. For
$\kappa _3$
is preserved. For
![]() $n \neq 4$
, the proof that
$n \neq 4$
, the proof that
![]() $\kappa _n = \aleph _n$
is identical to the proof of [Reference Neeman14, Lemma 4.24]. Since
$\kappa _n = \aleph _n$
is identical to the proof of [Reference Neeman14, Lemma 4.24]. Since
![]() $\kappa _1 = \aleph _1$
, and
$\kappa _1 = \aleph _1$
, and
![]() $\kappa _2 = \kappa _1^+$
in V, we need only check that
$\kappa _2 = \kappa _1^+$
in V, we need only check that
![]() $\kappa _2$
is not collapsed. This follows from [Reference Neeman14, Claims 4.18–4.21].
$\kappa _2$
is not collapsed. This follows from [Reference Neeman14, Claims 4.18–4.21].
The proof that
![]() $2^{\kappa _n} = \kappa _{n+2}$
for
$2^{\kappa _n} = \kappa _{n+2}$
for
![]() $n> 1$
is identical to the proof of [Reference Neeman14, Claim 4.28]. (Note that this proof relies on several claims and lemmas—while our construction is slightly different, the proofs of those claims and lemmas are identical.)
$n> 1$
is identical to the proof of [Reference Neeman14, Claim 4.28]. (Note that this proof relies on several claims and lemmas—while our construction is slightly different, the proofs of those claims and lemmas are identical.)
Lemma 5.4. In
![]() $V[A][U][S][e]$
, ITP holds at
$V[A][U][S][e]$
, ITP holds at
![]() $\aleph _{n+2}$
for all
$\aleph _{n+2}$
for all
![]() $n> 1$
.
$n> 1$
.
Proof The proof is exactly as in Section 3.3. While the model has changed slightly, the proofs of the various facts used are identical to the corresponding proofs in [Reference Neeman14] for
![]() $n \geq 2$
.
$n \geq 2$
.
Theorem 5.5. Let
![]() $\langle \kappa _n \mid 3 \leq n < \omega \rangle $
be an increasing sequence of supercompact cardinals with supremum
$\langle \kappa _n \mid 3 \leq n < \omega \rangle $
be an increasing sequence of supercompact cardinals with supremum
![]() $\nu $
. Then there is a forcing extension in which
$\nu $
. Then there is a forcing extension in which
![]() $\aleph _n = \kappa _n$
,
$\aleph _n = \kappa _n$
,
![]() $\aleph _\omega $
is strong limit,
$\aleph _\omega $
is strong limit,
![]() $(\nu ^+)^V = \aleph _{\omega +1}$
, and ITP holds at
$(\nu ^+)^V = \aleph _{\omega +1}$
, and ITP holds at
![]() $\aleph _{\omega +1}$
and at
$\aleph _{\omega +1}$
and at
![]() $\aleph _n$
for
$\aleph _n$
for
![]() $3 < n < \omega $
.
$3 < n < \omega $
.
Proof As before, we define an intermediate model
![]() $M = V[A_{[3,\omega )}][B_{[2,\omega )}][C_{[2,\omega )}]$
, and let
$M = V[A_{[3,\omega )}][B_{[2,\omega )}][C_{[2,\omega )}]$
, and let
![]() $\mathbb {L}_\mu = \operatorname {\mathrm {Add}}(\mu ^{++}, \kappa _4)^V \times \operatorname {\mathrm {Col}}(\mu ^{++},<\kappa _3) \times \operatorname {\mathrm {Col}}(\omega ,\mu )$
. Note that
$\mathbb {L}_\mu = \operatorname {\mathrm {Add}}(\mu ^{++}, \kappa _4)^V \times \operatorname {\mathrm {Col}}(\mu ^{++},<\kappa _3) \times \operatorname {\mathrm {Col}}(\omega ,\mu )$
. Note that
![]() $|\operatorname {\mathrm {Col}}(\omega , \mu )| < \mu ^+$
, and
$|\operatorname {\mathrm {Col}}(\omega , \mu )| < \mu ^+$
, and
![]() $\operatorname {\mathrm {Col}}(\mu ^{++}, <\kappa _3)$
is
$\operatorname {\mathrm {Col}}(\mu ^{++}, <\kappa _3)$
is
![]() $\mu ^{++}$
-closed.
$\mu ^{++}$
-closed.
Next, we need to verify that the remainder of the forcing is
![]() $\mu ^{++}$
-closed in M.
$\mu ^{++}$
-closed in M.
![]() $\operatorname {\mathrm {Add}}(\mu ^{++}, \kappa _4)^V$
is
$\operatorname {\mathrm {Add}}(\mu ^{++}, \kappa _4)^V$
is
![]() $\mu ^{++}$
-closed in V. To show that this poset is closed in M, we need to show that all of the intermediate posets are likewise closed.
$\mu ^{++}$
-closed in V. To show that this poset is closed in M, we need to show that all of the intermediate posets are likewise closed.
![]() $\mathbb {A}_{[3,\omega )}$
is
$\mathbb {A}_{[3,\omega )}$
is
![]() $\kappa _3$
-closed. By [Reference Neeman14, Claim 4.7], noting that
$\kappa _3$
-closed. By [Reference Neeman14, Claim 4.7], noting that
![]() $\mathbb {A}_0, \mathbb {A}_1, \mathbb {U}_0,$
and
$\mathbb {A}_0, \mathbb {A}_1, \mathbb {U}_0,$
and
![]() $\mathbb {U}_1$
are all trivial, we see that
$\mathbb {U}_1$
are all trivial, we see that
![]() $\mathbb {B}_{[2,\omega )}$
is
$\mathbb {B}_{[2,\omega )}$
is
![]() $\kappa _2 = \mu ^{++}$
-closed over V. Finally,
$\kappa _2 = \mu ^{++}$
-closed over V. Finally,
![]() $\mathbb {C}^{+B}\upharpoonright [\kappa _3, \nu )$
is
$\mathbb {C}^{+B}\upharpoonright [\kappa _3, \nu )$
is
![]() $\kappa _3$
-closed over
$\kappa _3$
-closed over
![]() $V[B]$
by [Reference Neeman14, Claim 4.15]. We conclude that
$V[B]$
by [Reference Neeman14, Claim 4.15]. We conclude that
![]() $\mathbb {L}_\mu $
is the product of a
$\mathbb {L}_\mu $
is the product of a
![]() $\mu ^{++}$
-closed poset with a poset of size
$\mu ^{++}$
-closed poset with a poset of size
![]() $<\mu ^+$
.
$<\mu ^+$
.
Since
![]() $\kappa _3$
is supercompact, and the posets adding the embeddings for
$\kappa _3$
is supercompact, and the posets adding the embeddings for
![]() $n> 3$
have suitably distributive powers, we meet the hypotheses of Theorem 4.6. It follows that there exists
$n> 3$
have suitably distributive powers, we meet the hypotheses of Theorem 4.6. It follows that there exists
![]() $\mu \in \operatorname {\mathrm {Index}}$
such that in the extension of M by
$\mu \in \operatorname {\mathrm {Index}}$
such that in the extension of M by
![]() $\mathbb {L}_{\mu }$
, ITP holds at
$\mathbb {L}_{\mu }$
, ITP holds at
![]() $\aleph _{\omega +1}$
.
$\aleph _{\omega +1}$
.
Let
![]() $A_2 \times S_1 \times e$
be generic for
$A_2 \times S_1 \times e$
be generic for
![]() $\mathbb {L}_\mu $
over M, and let
$\mathbb {L}_\mu $
over M, and let
![]() $A = A_2 \times A_{[3,\omega )}$
. Let
$A = A_2 \times A_{[3,\omega )}$
. Let
![]() $U = U_{[2,\omega )}$
be the upwards closure of
$U = U_{[2,\omega )}$
be the upwards closure of
![]() $B_{[2,\omega )}$
in
$B_{[2,\omega )}$
in
![]() $\mathbb {U}_{[2,\omega )}$
. Let
$\mathbb {U}_{[2,\omega )}$
. Let
![]() $S_{[2,\omega )}$
be the upwards closure of
$S_{[2,\omega )}$
be the upwards closure of
![]() $C_{[2,\omega )}$
in
$C_{[2,\omega )}$
in
![]() $\mathbb {C}_{[1,\omega )}^{+A\ast U}$
, and let
$\mathbb {C}_{[1,\omega )}^{+A\ast U}$
, and let
![]() $S = S_1 \times S_{[2,\omega )}$
. Let N be the model
$S = S_1 \times S_{[2,\omega )}$
. Let N be the model
![]() $V[A][U][S]$
.
$V[A][U][S]$
.
Claim 5.6. There is a
![]() $\mu ^+$
-closed extension
$\mu ^+$
-closed extension
![]() $N[G]$
of N such that G is still generic over
$N[G]$
of N such that G is still generic over
![]() $N[e]$
, both
$N[e]$
, both
![]() $\nu $
and
$\nu $
and
![]() $\nu ^+$
are still cardinals in
$\nu ^+$
are still cardinals in
![]() $N[e][G]$
, and
$N[e][G]$
, and
![]() $M[A_2 \times S_1 \times e]$
is contained in
$M[A_2 \times S_1 \times e]$
is contained in
![]() $N[e][G]$
.
$N[e][G]$
.
Proof Analogous to Proposition 3.33. The relevant forcing is the product of the factor forcing refining
![]() $U_{[2,\omega )}$
to a filter for
$U_{[2,\omega )}$
to a filter for
![]() $\mathbb {B}^{+A_2\ast U_2}\upharpoonright [\kappa _3, \nu )$
and the factor forcing refining
$\mathbb {B}^{+A_2\ast U_2}\upharpoonright [\kappa _3, \nu )$
and the factor forcing refining
![]() $S_{[2,\omega )}$
to a generic for
$S_{[2,\omega )}$
to a generic for
![]() $\mathbb {C}^{+A_2\ast U_2}\upharpoonright [\kappa _3, \nu )$
. These posets are in
$\mathbb {C}^{+A_2\ast U_2}\upharpoonright [\kappa _3, \nu )$
. These posets are in
![]() $V[A][U][S]$
. That they are
$V[A][U][S]$
. That they are
![]() $\mu ^+$
-closed in
$\mu ^+$
-closed in
![]() $V[A][U][S]$
follows from the proofs of [Reference Neeman14, Claims 4.9, 4.16, and 4.26]; preservation of cardinals follows from [Reference Neeman14, Claims 4.18–4.21].
$V[A][U][S]$
follows from the proofs of [Reference Neeman14, Claims 4.9, 4.16, and 4.26]; preservation of cardinals follows from [Reference Neeman14, Claims 4.18–4.21].
Claim 5.7. In
![]() $N[e]$
,
$N[e]$
,
![]() $ITP$
holds at
$ITP$
holds at
![]() $\nu ^+$
.
$\nu ^+$
.
Claim 5.8. In
![]() $N[e]$
,
$N[e]$
,
![]() $ITP$
holds at
$ITP$
holds at
![]() $\aleph _n$
for all
$\aleph _n$
for all
![]() $n \geq 4$
.
$n \geq 4$
.
Proof Immediate from Lemma 5.4.
We conclude that in
![]() $N[e]$
,
$N[e]$
,
![]() $\operatorname {\mathrm {ITP}}$
holds at
$\operatorname {\mathrm {ITP}}$
holds at
![]() $\aleph _{\omega +1}$
and at
$\aleph _{\omega +1}$
and at
![]() $\aleph _{n}$
for all
$\aleph _{n}$
for all
![]() $3 < n < \omega $
, completing the proof.
$3 < n < \omega $
, completing the proof.
6. Successors of singular cardinals of multiple cofinalities
Given any regular cardinal
![]() $\tau $
, along with
$\tau $
, along with
![]() $\tau $
-many supercompact cardinals, we can apply the techniques of the previous sections to obtain the strong or super tree properties at
$\tau $
-many supercompact cardinals, we can apply the techniques of the previous sections to obtain the strong or super tree properties at
![]() $\aleph _{{\tau }+1}$
. If we try to apply these techniques for multiple cofinalities
$\aleph _{{\tau }+1}$
. If we try to apply these techniques for multiple cofinalities
![]() $\tau _0$
and
$\tau _0$
and
![]() $\tau _1$
simultaneously, there is a major obstacle: in the resulting model,
$\tau _1$
simultaneously, there is a major obstacle: in the resulting model,
![]() $\tau _1$
will be collapsed to
$\tau _1$
will be collapsed to
![]() $\tau _0$
, so
$\tau _0$
, so
![]() $\aleph _{\tau _1}$
will only have cofinality
$\aleph _{\tau _1}$
will only have cofinality
![]() $\tau _0$
. Instead, if
$\tau _0$
. Instead, if
![]() $\tau _1$
is of the form
$\tau _1$
is of the form
![]() $\omega _{\alpha _1}$
for some successor ordinal
$\omega _{\alpha _1}$
for some successor ordinal
![]() $\alpha _1$
, we can ensure that
$\alpha _1$
, we can ensure that
![]() $\aleph _{\omega _{\alpha _1}+1}$
as computed in the final model has ITP. In fact, this can be done for finitely many such cardinals.
$\aleph _{\omega _{\alpha _1}+1}$
as computed in the final model has ITP. In fact, this can be done for finitely many such cardinals.
In this section, given any finite sequence
![]() $\alpha _0, \dots , \alpha _n$
of ordinals where
$\alpha _0, \dots , \alpha _n$
of ordinals where
![]() $\alpha _i < \omega _{\alpha _i}$
and
$\alpha _i < \omega _{\alpha _i}$
and
![]() $\aleph _{\alpha _i}$
is a regular cardinal, we construct a model where the strong tree property or ITP hold at each
$\aleph _{\alpha _i}$
is a regular cardinal, we construct a model where the strong tree property or ITP hold at each
![]() $\aleph _{\omega _{\alpha _n}+1}$
simultaneously. First we demonstrate the construction for
$\aleph _{\omega _{\alpha _n}+1}$
simultaneously. First we demonstrate the construction for
![]() $\aleph _{\omega +1}$
and
$\aleph _{\omega +1}$
and
![]() $\aleph _{\omega _1+1}$
, and then we present the construction in full generality. Note that the large cardinal hypotheses are somewhat stronger than might be expected; we require supercompact-many supercompacts, instead of
$\aleph _{\omega _1+1}$
, and then we present the construction in full generality. Note that the large cardinal hypotheses are somewhat stronger than might be expected; we require supercompact-many supercompacts, instead of
![]() $\omega _1$
-many supercompacts. This is because we want to obtain ITP at
$\omega _1$
-many supercompacts. This is because we want to obtain ITP at
![]() $\aleph _{\omega _1+1}$
in our final model
$\aleph _{\omega _1+1}$
in our final model
![]() $V[H][\mathbb {L}_{\mu ,\delta }]$
, which will be defined below. In this model,
$V[H][\mathbb {L}_{\mu ,\delta }]$
, which will be defined below. In this model,
![]() $\omega _1 = \mu ^+$
, so we require
$\omega _1 = \mu ^+$
, so we require
![]() $\mu ^+$
-many supercompact cardinals; since
$\mu ^+$
-many supercompact cardinals; since
![]() $\mu $
is not fixed ahead of time, and the only upper bound we have is
$\mu $
is not fixed ahead of time, and the only upper bound we have is
![]() $\kappa _0$
, we need
$\kappa _0$
, we need
![]() $\kappa _0$
-many supercompacts. The same argument, using only
$\kappa _0$
-many supercompacts. The same argument, using only
![]() $\omega _1$
-many supercompacts, can obtain ITP at
$\omega _1$
-many supercompacts, can obtain ITP at
![]() $\aleph _{(\omega _1)^V+1}$
, but since
$\aleph _{(\omega _1)^V+1}$
, but since
![]() $(\omega _1)^V$
is collapsed by
$(\omega _1)^V$
is collapsed by
![]() $\mathbb {L}_\mu $
(for all
$\mathbb {L}_\mu $
(for all
![]() $\mu> \omega $
) this will be the successor of a singular of only countable cofinality.
$\mu> \omega $
) this will be the successor of a singular of only countable cofinality.
Theorem 6.1. Let
![]() $\kappa _0$
be indestructibly supercompact, and let
$\kappa _0$
be indestructibly supercompact, and let
![]() $\langle \kappa _\rho \mid \rho < \kappa _0 \rangle $
be an increasing continuous sequence of cardinals such that the following holds
$\langle \kappa _\rho \mid \rho < \kappa _0 \rangle $
be an increasing continuous sequence of cardinals such that the following holds
![]() $:$
$:$
-
•
 $\kappa _{\rho +1} = \kappa _{\rho }^+$
for all limit ordinals
$\kappa _{\rho +1} = \kappa _{\rho }^+$
for all limit ordinals
 $\rho < \kappa _0.$
$\rho < \kappa _0.$
-
•
 $\kappa _n$
is indestructibly supercompact for all
$\kappa _n$
is indestructibly supercompact for all
 $n < \omega .$
$n < \omega .$
-
•
 $\kappa _{\rho +2}$
is indestructibly supercompact for all
$\kappa _{\rho +2}$
is indestructibly supercompact for all
 $\omega \leq \rho < \kappa _0$
.
$\omega \leq \rho < \kappa _0$
.
Then there is a generic extension in which ITP holds at
![]() $\aleph _{\omega _1+1}$
and the strong tree property holds at
$\aleph _{\omega _1+1}$
and the strong tree property holds at
![]() $\aleph _{\omega +1}$
.
$\aleph _{\omega +1}$
.
Proof As in Corollary 4.8, we define
 $$\begin{align*}\mathbb{H} = \left(\prod_{\rho<\omega} \operatorname{\mathrm{Col}}(\kappa_\rho, <\kappa_{\rho+1})\right) \times \left(\prod_{\omega\leq\rho<\kappa_0} \operatorname{\mathrm{Col}}(\kappa_{\rho+1}, <\kappa_{\rho+2})\right).\end{align*}$$
$$\begin{align*}\mathbb{H} = \left(\prod_{\rho<\omega} \operatorname{\mathrm{Col}}(\kappa_\rho, <\kappa_{\rho+1})\right) \times \left(\prod_{\omega\leq\rho<\kappa_0} \operatorname{\mathrm{Col}}(\kappa_{\rho+1}, <\kappa_{\rho+2})\right).\end{align*}$$
Let H be generic for
![]() $\mathbb {H}$
. Let
$\mathbb {H}$
. Let
![]() $\operatorname {\mathrm {Index}} = \{(\mu , \delta ) \mid \operatorname {\mathrm {cf}}(\mu ) = \omega , \operatorname {\mathrm {cf}}(\delta ) = \mu ^+, \mu < \delta < \kappa _0\}.$
For each pair
$\operatorname {\mathrm {Index}} = \{(\mu , \delta ) \mid \operatorname {\mathrm {cf}}(\mu ) = \omega , \operatorname {\mathrm {cf}}(\delta ) = \mu ^+, \mu < \delta < \kappa _0\}.$
For each pair
![]() $(\mu , \delta ) \in \operatorname {\mathrm {Index}}$
, let
$(\mu , \delta ) \in \operatorname {\mathrm {Index}}$
, let
![]() $\mathbb {L}_{\mu ,\delta } = \operatorname {\mathrm {Col}}(\omega , \mu ) \times \operatorname {\mathrm {Col}}(\mu ^+, \delta ) \times \operatorname {\mathrm {Col}}(\delta ^{++}, <\kappa _0)$
. We wish to find
$\mathbb {L}_{\mu ,\delta } = \operatorname {\mathrm {Col}}(\omega , \mu ) \times \operatorname {\mathrm {Col}}(\mu ^+, \delta ) \times \operatorname {\mathrm {Col}}(\delta ^{++}, <\kappa _0)$
. We wish to find
![]() $(\mu , \delta ) \in \operatorname {\mathrm {Index}}$
such that in the generic extension of
$(\mu , \delta ) \in \operatorname {\mathrm {Index}}$
such that in the generic extension of
![]() $V[H]$
by
$V[H]$
by
![]() $\mathbb {L}_{\mu ,\delta }$
, ITP holds at
$\mathbb {L}_{\mu ,\delta }$
, ITP holds at
![]() $\aleph _{\omega _1+1}$
and the strong tree property holds at
$\aleph _{\omega _1+1}$
and the strong tree property holds at
![]() $\aleph _{\omega +1}$
.
$\aleph _{\omega +1}$
.
Let I be the projection of
![]() $\operatorname {\mathrm {Index}}$
to the first coordinate. For all
$\operatorname {\mathrm {Index}}$
to the first coordinate. For all
![]() $\mu \in I$
, let
$\mu \in I$
, let
![]() $I_\mu = \{\delta \mid \mu < \delta < \kappa _0, \operatorname {\mathrm {cf}}(\delta ) = \mu ^+\}$
. For each
$I_\mu = \{\delta \mid \mu < \delta < \kappa _0, \operatorname {\mathrm {cf}}(\delta ) = \mu ^+\}$
. For each
![]() $\mu \in I$
, consider the initial segment
$\mu \in I$
, consider the initial segment
![]() $\langle \kappa _\rho \mid \rho < \mu ^+ \rangle $
, with supremum
$\langle \kappa _\rho \mid \rho < \mu ^+ \rangle $
, with supremum
![]() $\nu _\mu \mathrel {\mathop :}= \kappa _{\mu ^+}$
. We now verify the hypotheses of Theorem 4.6.
$\nu _\mu \mathrel {\mathop :}= \kappa _{\mu ^+}$
. We now verify the hypotheses of Theorem 4.6.
For any
![]() $\delta \in I_\mu $
,
$\delta \in I_\mu $
,
![]() $\operatorname {\mathrm {Col}}(\omega , \mu ) \times \operatorname {\mathrm {Col}}(\mu ^+, \delta )$
has size
$\operatorname {\mathrm {Col}}(\omega , \mu ) \times \operatorname {\mathrm {Col}}(\mu ^+, \delta )$
has size
![]() $< \delta ^+$
, while
$< \delta ^+$
, while
![]() $\operatorname {\mathrm {Col}}(\delta ^{++}, <\kappa _0)$
is
$\operatorname {\mathrm {Col}}(\delta ^{++}, <\kappa _0)$
is
![]() $\delta ^{++}$
-closed; moreover
$\delta ^{++}$
-closed; moreover
![]() $|\mathbb {L}_{\mu ,\delta }|<\kappa _2$
.
$|\mathbb {L}_{\mu ,\delta }|<\kappa _2$
.
In
![]() $V[H]$
,
$V[H]$
,
![]() $\kappa _0$
is
$\kappa _0$
is
![]() $\nu _\mu ^+$
-supercompact; let i be the corresponding embedding. Noting that
$\nu _\mu ^+$
-supercompact; let i be the corresponding embedding. Noting that
![]() $[x \mapsto \kappa _x^{+\mu ^+}]_{U_0} = \nu _\mu $
, and
$[x \mapsto \kappa _x^{+\mu ^+}]_{U_0} = \nu _\mu $
, and
![]() $\kappa _x^{+\mu ^+} \in I_\mu $
, we conclude that
$\kappa _x^{+\mu ^+} \in I_\mu $
, we conclude that
![]() $\nu _\mu \in i(I_\mu )$
. Note also that there are generic supercompactness embeddings
$\nu _\mu \in i(I_\mu )$
. Note also that there are generic supercompactness embeddings
![]() $j_{\rho +2}$
added by
$j_{\rho +2}$
added by
![]() $\operatorname {\mathrm {Col}}(\kappa _{\rho +1}, j(\kappa _{\rho +3}))$
. This poset is
$\operatorname {\mathrm {Col}}(\kappa _{\rho +1}, j(\kappa _{\rho +3}))$
. This poset is
![]() $\kappa _{\rho +1}$
-closed in
$\kappa _{\rho +1}$
-closed in
![]() $V[H\upharpoonright [\rho +2, \kappa _0)]$
, and
$V[H\upharpoonright [\rho +2, \kappa _0)]$
, and
![]() $V[H]$
is a
$V[H]$
is a
![]() $\kappa _{\rho +1}$
-cc extension of this poset, so in particular the product
$\kappa _{\rho +1}$
-cc extension of this poset, so in particular the product
![]() $\operatorname {\mathrm {Col}}(\kappa _{\rho +1}, j(\kappa _{\rho +3}))^{\kappa _\rho }$
is
$\operatorname {\mathrm {Col}}(\kappa _{\rho +1}, j(\kappa _{\rho +3}))^{\kappa _\rho }$
is
![]() $<\kappa _\rho $
-distributive.
$<\kappa _\rho $
-distributive.
Thus for each
![]() $\mu \in I$
, we can apply Theorem 4.6 with respect to this initial segment and
$\mu \in I$
, we can apply Theorem 4.6 with respect to this initial segment and
![]() $I_\mu $
to conclude that there exists some
$I_\mu $
to conclude that there exists some
![]() $\delta _\mu \in I_\mu $
such that ITP holds at
$\delta _\mu \in I_\mu $
such that ITP holds at
![]() $\nu _\mu ^+$
in the generic extension of
$\nu _\mu ^+$
in the generic extension of
![]() $V[H]$
by
$V[H]$
by
![]() $\mathbb {L}_{\mu ,\delta _\mu }$
.
$\mathbb {L}_{\mu ,\delta _\mu }$
.
We will now pin down the first coordinate. Consider the initial segment
![]() $\langle \kappa _i \mid i<\omega \rangle $
, with supremum
$\langle \kappa _i \mid i<\omega \rangle $
, with supremum
![]() $\nu \mathrel {\mathop :}= \kappa _\omega $
. In
$\nu \mathrel {\mathop :}= \kappa _\omega $
. In
![]() $V[H]$
,
$V[H]$
,
![]() $\kappa _0$
is
$\kappa _0$
is
![]() $\nu ^+$
-supercompact; let i be the corresponding embedding. Noting that
$\nu ^+$
-supercompact; let i be the corresponding embedding. Noting that
![]() $[x \mapsto \kappa _x^{+\omega }]_{U_0} = \nu $
, and
$[x \mapsto \kappa _x^{+\omega }]_{U_0} = \nu $
, and
![]() $\kappa _x^{+\omega }$
is in I, we conclude that
$\kappa _x^{+\omega }$
is in I, we conclude that
![]() $\nu \in i(I)$
. Note also that
$\nu \in i(I)$
. Note also that
![]() $|\mathbb {L}_{\mu , \delta _\mu }| < \kappa _2$
for all
$|\mathbb {L}_{\mu , \delta _\mu }| < \kappa _2$
for all
![]() $\mu \in I$
, so we also meet the hypothesis of Theorem 3.14 (with respect to the first
$\mu \in I$
, so we also meet the hypothesis of Theorem 3.14 (with respect to the first
![]() $\omega $
-many supercompacts, using I as our index set). Thus there exists
$\omega $
-many supercompacts, using I as our index set). Thus there exists
![]() $\mu \in I$
such that the strong tree property holds at
$\mu \in I$
such that the strong tree property holds at
![]() $\nu ^+$
in the extension of
$\nu ^+$
in the extension of
![]() $V[H]$
by
$V[H]$
by
![]() $\mathbb {L}_{\mu , \delta _\mu }$
. Note that the pair
$\mathbb {L}_{\mu , \delta _\mu }$
. Note that the pair
![]() $(\mu , \delta _\mu )$
is in
$(\mu , \delta _\mu )$
is in
![]() $\operatorname {\mathrm {Index}}$
. Then in the extension of
$\operatorname {\mathrm {Index}}$
. Then in the extension of
![]() $V[H]$
by a generic L for
$V[H]$
by a generic L for
![]() $\mathbb {L}_{\mu , \delta _\mu }$
, ITP will hold at
$\mathbb {L}_{\mu , \delta _\mu }$
, ITP will hold at
![]() $\nu _\mu ^+$
, and the strong tree property will hold at
$\nu _\mu ^+$
, and the strong tree property will hold at
![]() $\nu ^+$
.
$\nu ^+$
.
To finish the proof, we examine the cardinal structure in the new model. In
![]() $V[H][L]$
,
$V[H][L]$
,
![]() $\mu $
is collapsed to
$\mu $
is collapsed to
![]() $\omega $
, so
$\omega $
, so
![]() $\mu ^+ = \aleph _1$
. The other parameter
$\mu ^+ = \aleph _1$
. The other parameter
![]() $\delta $
is collapsed to
$\delta $
is collapsed to
![]() $\mu ^+$
, so
$\mu ^+$
, so
![]() $\delta ^+ = \mu ^{++} = \aleph _2$
. After forcing with
$\delta ^+ = \mu ^{++} = \aleph _2$
. After forcing with
![]() $\mathbb {H}$
, we have that
$\mathbb {H}$
, we have that
![]() $\kappa _{\rho ^+} = \kappa _{\rho +1}$
for all
$\kappa _{\rho ^+} = \kappa _{\rho +1}$
for all
![]() $\rho < \nu $
, and in
$\rho < \nu $
, and in
![]() $V[H][L]$
,
$V[H][L]$
,
![]() $\kappa _0$
becomes
$\kappa _0$
becomes
![]() $\aleph _4$
. We conclude that since
$\aleph _4$
. We conclude that since
![]() $\kappa _\omega ^+$
is the successor of the limit of
$\kappa _\omega ^+$
is the successor of the limit of
![]() $\langle \kappa _n \mid n < \omega \rangle $
,
$\langle \kappa _n \mid n < \omega \rangle $
,
![]() $\nu ^+ = \aleph _{w+1}$
. Similarly,
$\nu ^+ = \aleph _{w+1}$
. Similarly,
![]() $\nu _\mu ^+$
is the successor of the limit of
$\nu _\mu ^+$
is the successor of the limit of
![]() $\langle \kappa _\rho \mid \rho < \omega _1\rangle $
, so
$\langle \kappa _\rho \mid \rho < \omega _1\rangle $
, so
![]() $\nu _\mu ^+ = \aleph _{\omega _1+1}$
.
$\nu _\mu ^+ = \aleph _{\omega _1+1}$
.
Now we generalize this argument to apply to any finite sequence of cofinalities.
Theorem 6.2. Let
![]() $\alpha _0, \dots , \alpha _n$
be an increasing sequence of ordinals, such that for all
$\alpha _0, \dots , \alpha _n$
be an increasing sequence of ordinals, such that for all
![]() $i\leq n$
,
$i\leq n$
,
![]() $\omega _{\alpha _i}$
is a regular cardinal with
$\omega _{\alpha _i}$
is a regular cardinal with
![]() $\alpha _i < \omega _{\alpha _i}$
. Let
$\alpha _i < \omega _{\alpha _i}$
. Let
![]() $\kappa _0$
be indestructibly supercompact, and let
$\kappa _0$
be indestructibly supercompact, and let
![]() $\langle \kappa _\rho \mid \rho < \kappa _0 \rangle $
be an increasing continuous sequence of cardinals such that the following holds
$\langle \kappa _\rho \mid \rho < \kappa _0 \rangle $
be an increasing continuous sequence of cardinals such that the following holds
![]() $:$
$:$
-
•
 $\kappa _{\rho +1} = \kappa _{\rho }^+$
for all limit ordinals
$\kappa _{\rho +1} = \kappa _{\rho }^+$
for all limit ordinals
 $\rho < \kappa _0.$
$\rho < \kappa _0.$
-
•
 $\kappa _n$
is indestructibly supercompact for all
$\kappa _n$
is indestructibly supercompact for all
 $n < \omega .$
$n < \omega .$
-
•
 $\kappa _{\rho +2}$
is indestructibly supercompact for all
$\kappa _{\rho +2}$
is indestructibly supercompact for all
 $\omega \leq \rho < \kappa _0.$
$\omega \leq \rho < \kappa _0.$
Then there is a generic extension in which the strong tree property holds at
![]() $\aleph _{\omega _{\alpha _i}+1}$
for all
$\aleph _{\omega _{\alpha _i}+1}$
for all
![]() $i \leq n$
. In addition, if
$i \leq n$
. In addition, if
![]() $\alpha _{i+1}> \alpha _i+1$
, then ITP holds at
$\alpha _{i+1}> \alpha _i+1$
, then ITP holds at
![]() $\aleph _{\omega _{\alpha _i}+1}$
.
$\aleph _{\omega _{\alpha _i}+1}$
.
Proof We define
 $$\begin{align*}\mathbb{H} = \left(\prod_{\rho<\omega} \operatorname{\mathrm{Col}}(\kappa_\rho, <\kappa_{\rho+1})\right) \times \left(\prod_{\omega\leq\rho<\kappa_0} \operatorname{\mathrm{Col}}(\kappa_{\rho+1}, <\kappa_{\rho+2})\right).\end{align*}$$
$$\begin{align*}\mathbb{H} = \left(\prod_{\rho<\omega} \operatorname{\mathrm{Col}}(\kappa_\rho, <\kappa_{\rho+1})\right) \times \left(\prod_{\omega\leq\rho<\kappa_0} \operatorname{\mathrm{Col}}(\kappa_{\rho+1}, <\kappa_{\rho+2})\right).\end{align*}$$
Let H be generic for
![]() $\mathbb {H}$
. For all
$\mathbb {H}$
. For all
![]() $0 \leq i < n$
, define
$0 \leq i < n$
, define
![]() $f(i)$
as the unique ordinal
$f(i)$
as the unique ordinal
![]() $\beta $
such that
$\beta $
such that
![]() $\alpha _{i+1} = \alpha _{i}+\beta $
. In particular, this means that
$\alpha _{i+1} = \alpha _{i}+\beta $
. In particular, this means that
![]() $\omega _{\alpha _{i+1}} = \omega _{\alpha _i}^{+f(i)}$
. Let
$\omega _{\alpha _{i+1}} = \omega _{\alpha _i}^{+f(i)}$
. Let
![]() $\operatorname {\mathrm {Index}}$
be the set of all increasing sequences
$\operatorname {\mathrm {Index}}$
be the set of all increasing sequences
![]() $s = \langle \delta _i \mid i \leq n\rangle $
such that
$s = \langle \delta _i \mid i \leq n\rangle $
such that
![]() $\delta _n < \kappa _0$
,
$\delta _n < \kappa _0$
,
![]() $\operatorname {\mathrm {cf}}(\delta _0) = \omega _{\alpha _0}$
, and for all
$\operatorname {\mathrm {cf}}(\delta _0) = \omega _{\alpha _0}$
, and for all
![]() $0 \leq i < n$
,
$0 \leq i < n$
,
![]() $\operatorname {\mathrm {cf}}(\delta _{i+1}) = \delta _i^{+f(i)}$
. For all
$\operatorname {\mathrm {cf}}(\delta _{i+1}) = \delta _i^{+f(i)}$
. For all
![]() $s \in \operatorname {\mathrm {Index}}$
, in V we define
$s \in \operatorname {\mathrm {Index}}$
, in V we define
 $$\begin{align*}\mathbb{L}_s \mathrel{\mathop:}= \operatorname{\mathrm{Col}}(\omega_{\alpha_0}, \delta_0) \times \left(\prod_{1\leq i < n} \operatorname{\mathrm{Col}}(\operatorname{\mathrm{cf}}(\delta_{i}), \delta_{i})\right) \times \operatorname{\mathrm{Col}}(\delta_n^{++}, <\kappa_0).\end{align*}$$
$$\begin{align*}\mathbb{L}_s \mathrel{\mathop:}= \operatorname{\mathrm{Col}}(\omega_{\alpha_0}, \delta_0) \times \left(\prod_{1\leq i < n} \operatorname{\mathrm{Col}}(\operatorname{\mathrm{cf}}(\delta_{i}), \delta_{i})\right) \times \operatorname{\mathrm{Col}}(\delta_n^{++}, <\kappa_0).\end{align*}$$
Note that for all
![]() $s \in \operatorname {\mathrm {Index}}$
,
$s \in \operatorname {\mathrm {Index}}$
,
![]() $|\mathbb {L}_s| < \kappa _2$
.
$|\mathbb {L}_s| < \kappa _2$
.
We wish to show that there exists
![]() $s \in \operatorname {\mathrm {Index}}$
so that in the extension of
$s \in \operatorname {\mathrm {Index}}$
so that in the extension of
![]() $V[H]$
by
$V[H]$
by
![]() $\mathbb {L}_s$
, the strong tree property holds at
$\mathbb {L}_s$
, the strong tree property holds at
![]() $\aleph _{\omega _{\alpha _i}+1}$
for all
$\aleph _{\omega _{\alpha _i}+1}$
for all
![]() $i \leq n$
, and if
$i \leq n$
, and if
![]() $\alpha _{i+1}> (\alpha _i)+1$
, then ITP holds at
$\alpha _{i+1}> (\alpha _i)+1$
, then ITP holds at
![]() $\aleph _{\omega _{\alpha _i}+1}$
.
$\aleph _{\omega _{\alpha _i}+1}$
.
First, we note that in
![]() $V[H]$
, for any
$V[H]$
, for any
![]() $\lambda \geq \nu ^+$
, there are generic
$\lambda \geq \nu ^+$
, there are generic
![]() $\lambda $
-supercompactness embeddings
$\lambda $
-supercompactness embeddings
![]() $j_{\rho +2}$
with critical point
$j_{\rho +2}$
with critical point
![]() $\kappa _{\rho +2}$
added by
$\kappa _{\rho +2}$
added by
![]() $\operatorname {\mathrm {Col}}(\kappa _{\rho +1}, j(\kappa _{\rho +3}))$
. This poset is
$\operatorname {\mathrm {Col}}(\kappa _{\rho +1}, j(\kappa _{\rho +3}))$
. This poset is
![]() $\kappa _{\rho +1}$
-closed in
$\kappa _{\rho +1}$
-closed in
![]() $V[H\upharpoonright [\rho +2, \kappa _0)]$
, and
$V[H\upharpoonright [\rho +2, \kappa _0)]$
, and
![]() $V[H]$
is a
$V[H]$
is a
![]() $\kappa _{\rho +1}$
-cc extension of this poset, so in particular the full support product
$\kappa _{\rho +1}$
-cc extension of this poset, so in particular the full support product
![]() $\operatorname {\mathrm {Col}}(\kappa _{\rho +1}, j(\kappa _{\rho +3}))^{\kappa _\rho }$
is
$\operatorname {\mathrm {Col}}(\kappa _{\rho +1}, j(\kappa _{\rho +3}))^{\kappa _\rho }$
is
![]() $<\kappa _\rho $
-distributive in
$<\kappa _\rho $
-distributive in
![]() $V[H]$
. Note also that in
$V[H]$
. Note also that in
![]() $V[H]$
,
$V[H]$
,
![]() $\kappa _0$
is supercompact. Let
$\kappa _0$
is supercompact. Let
![]() $\pi $
be a
$\pi $
be a
![]() $\nu ^+$
-supercompactness embedding with critical point
$\nu ^+$
-supercompactness embedding with critical point
![]() $\kappa $
.
$\kappa $
.
We need to choose
![]() $\delta _i$
for all i; we do so inductively, beginning at
$\delta _i$
for all i; we do so inductively, beginning at
![]() $\delta _n$
and working downwards.
$\delta _n$
and working downwards.
For every fixed
![]() $s = \langle \delta _0, \dots , \delta _{n-1}\rangle $
in the projection of
$s = \langle \delta _0, \dots , \delta _{n-1}\rangle $
in the projection of
![]() $\operatorname {\mathrm {Index}}$
to the first n components, let
$\operatorname {\mathrm {Index}}$
to the first n components, let
![]() $\delta _n^* = \delta _{n-1}^{+f(n-1)}$
, and let
$\delta _n^* = \delta _{n-1}^{+f(n-1)}$
, and let
![]() $I_s = \{\delta < \kappa _0 \mid \operatorname {\mathrm {cf}}(\delta ) = \delta ^*_n\}$
. Note that for all
$I_s = \{\delta < \kappa _0 \mid \operatorname {\mathrm {cf}}(\delta ) = \delta ^*_n\}$
. Note that for all
![]() $\delta \in I_{s}$
,
$\delta \in I_{s}$
,
![]() $s^\smallfrown \delta \in \operatorname {\mathrm {Index}}$
. Consider the initial segment
$s^\smallfrown \delta \in \operatorname {\mathrm {Index}}$
. Consider the initial segment
![]() $\langle \kappa _\rho \mid \rho < \delta _n^*\rangle $
, and let
$\langle \kappa _\rho \mid \rho < \delta _n^*\rangle $
, and let
![]() $\nu _s^n$
be the supremum of this sequence.
$\nu _s^n$
be the supremum of this sequence.
Note that for each
![]() $\delta \in I_{s}$
,
$\delta \in I_{s}$
,
![]() $\operatorname {\mathrm {Col}}(\delta _n^{++}, <\kappa _0)$
is
$\operatorname {\mathrm {Col}}(\delta _n^{++}, <\kappa _0)$
is
![]() $\delta ^{++}$
-closed, and the remainder of
$\delta ^{++}$
-closed, and the remainder of
![]() $\mathbb {L}_{s^\smallfrown \delta }$
has size
$\mathbb {L}_{s^\smallfrown \delta }$
has size
![]() $< \delta ^+$
. Note also that
$< \delta ^+$
. Note also that
![]() $\kappa _x^{+\delta ^*}$
is in
$\kappa _x^{+\delta ^*}$
is in
![]() $I_{s}$
for all x, so
$I_{s}$
for all x, so
![]() $\nu _s^n \in \pi (I_s)$
. Then applying Theorem 4.6, we conclude that for each sequence s, there exists some
$\nu _s^n \in \pi (I_s)$
. Then applying Theorem 4.6, we conclude that for each sequence s, there exists some
![]() $\delta ^s_n \in I_{s}$
such that in the extension of
$\delta ^s_n \in I_{s}$
such that in the extension of
![]() $V[H]$
by
$V[H]$
by
![]() $\mathbb {L}_{s^\smallfrown \delta ^s_n}$
, ITP holds at
$\mathbb {L}_{s^\smallfrown \delta ^s_n}$
, ITP holds at
![]() $(\nu _s^n)^+$
.
$(\nu _s^n)^+$
.
Now let
![]() $0 < k < n$
, and let s be a fixed sequence
$0 < k < n$
, and let s be a fixed sequence
![]() $\langle \delta _0, \dots , \delta _{k-1}\rangle $
in the projection of
$\langle \delta _0, \dots , \delta _{k-1}\rangle $
in the projection of
![]() $\operatorname {\mathrm {Index}}$
to the first k components. Let
$\operatorname {\mathrm {Index}}$
to the first k components. Let
![]() $\nu _s^i = \sup \langle \kappa _\rho \mid \rho < \operatorname {\mathrm {cf}}(\delta _i)\rangle $
. Let
$\nu _s^i = \sup \langle \kappa _\rho \mid \rho < \operatorname {\mathrm {cf}}(\delta _i)\rangle $
. Let
![]() $\delta _k^* = \delta _{k-1}^{+f(k-1)}$
and let
$\delta _k^* = \delta _{k-1}^{+f(k-1)}$
and let
![]() $I_s = \{\delta < \kappa _0 \mid \operatorname {\mathrm {cf}}(\delta ) = \delta _k^*\}.$
Working inductively, assume that for all
$I_s = \{\delta < \kappa _0 \mid \operatorname {\mathrm {cf}}(\delta ) = \delta _k^*\}.$
Working inductively, assume that for all
![]() $\delta \in I_s$
we have determined a sequence
$\delta \in I_s$
we have determined a sequence
![]() $s^{\prime }_\delta = \langle \delta _i \mid k < i \leq n\rangle $
of length
$s^{\prime }_\delta = \langle \delta _i \mid k < i \leq n\rangle $
of length
![]() $n-k$
such that the sequence
$n-k$
such that the sequence
![]() $s_\delta = s ^\smallfrown \delta ^\smallfrown s^{\prime }_\delta $
is in
$s_\delta = s ^\smallfrown \delta ^\smallfrown s^{\prime }_\delta $
is in
![]() $\operatorname {\mathrm {Index}}$
, and in the extension of
$\operatorname {\mathrm {Index}}$
, and in the extension of
![]() $V[H]$
by
$V[H]$
by
![]() $\mathbb {L}_{s_\delta }$
, ITP or the strong tree property holds at
$\mathbb {L}_{s_\delta }$
, ITP or the strong tree property holds at
![]() $\nu _{s_\delta }^i$
for all
$\nu _{s_\delta }^i$
for all
![]() $k < i \leq n$
.
$k < i \leq n$
.
Consider the initial segment
![]() $\langle \kappa _\rho \mid \rho < \delta _{k-1}^{+f(k)}\rangle $
, and let
$\langle \kappa _\rho \mid \rho < \delta _{k-1}^{+f(k)}\rangle $
, and let
![]() $\nu _s^k$
be the supremum of this sequence. Note that
$\nu _s^k$
be the supremum of this sequence. Note that
![]() $\kappa _x^{+\delta _k^*}$
is in
$\kappa _x^{+\delta _k^*}$
is in
![]() $I_{s}$
for all x, so
$I_{s}$
for all x, so
![]() $\nu _s^n \in i(I_s)$
.
$\nu _s^n \in i(I_s)$
.
We factor
![]() $\mathbb {L}_{s_\delta }$
as
$\mathbb {L}_{s_\delta }$
as
![]() $\mathbb {L}_s^0 \times \mathbb {L}_s^1$
, where each term is defined as follows, with
$\mathbb {L}_s^0 \times \mathbb {L}_s^1$
, where each term is defined as follows, with
![]() $\delta _k$
denoting
$\delta _k$
denoting
![]() $\delta $
:
$\delta $
:
 $$ \begin{align*} \mathbb{L}_{s_\delta}^0 &\mathrel{\mathop:}= \operatorname{\mathrm{Col}}(\omega_{\alpha_0}, \delta_0) \times \prod_{1 \leq i \leq k} \operatorname{\mathrm{Col}}(\operatorname{\mathrm{cf}}(\delta_{i}), \delta_{i}), \\[5pt] \mathbb{L}_{s_\delta}^1 &\mathrel{\mathop:}= \left(\prod_{k < i < n } \operatorname{\mathrm{Col}}(\operatorname{\mathrm{cf}}(\delta_{i}), \delta_{i})\right) \times \operatorname{\mathrm{Col}}(\delta_n^{++}, <\kappa_0). \end{align*} $$
$$ \begin{align*} \mathbb{L}_{s_\delta}^0 &\mathrel{\mathop:}= \operatorname{\mathrm{Col}}(\omega_{\alpha_0}, \delta_0) \times \prod_{1 \leq i \leq k} \operatorname{\mathrm{Col}}(\operatorname{\mathrm{cf}}(\delta_{i}), \delta_{i}), \\[5pt] \mathbb{L}_{s_\delta}^1 &\mathrel{\mathop:}= \left(\prod_{k < i < n } \operatorname{\mathrm{Col}}(\operatorname{\mathrm{cf}}(\delta_{i}), \delta_{i})\right) \times \operatorname{\mathrm{Col}}(\delta_n^{++}, <\kappa_0). \end{align*} $$
Note that for all
![]() $\delta \in I_s$
,
$\delta \in I_s$
,
![]() $|\mathbb {L}_{s_\delta }^0| < \delta ^+$
. If
$|\mathbb {L}_{s_\delta }^0| < \delta ^+$
. If
![]() $\alpha _i> \alpha _{i}+1$
, then
$\alpha _i> \alpha _{i}+1$
, then
![]() $\operatorname {\mathrm {cf}}(\delta _{k+1})> \delta ^+$
, so we see that
$\operatorname {\mathrm {cf}}(\delta _{k+1})> \delta ^+$
, so we see that
![]() $\mathbb {L}_{s_\delta }^1$
is
$\mathbb {L}_{s_\delta }^1$
is
![]() $\delta ^{++}$
-closed. We apply Theorem 4.6 to choose some
$\delta ^{++}$
-closed. We apply Theorem 4.6 to choose some
![]() $\delta _k \in I_s$
such that in the extension of
$\delta _k \in I_s$
such that in the extension of
![]() $V[H]$
by
$V[H]$
by
![]() $\mathbb {L}_{s,\delta _k}$
, ITP holds at
$\mathbb {L}_{s,\delta _k}$
, ITP holds at
![]() $(\nu _s^k)^+$
.
$(\nu _s^k)^+$
.
If
![]() $\operatorname {\mathrm {cf}}(\delta _{k+1}) = \delta ^+$
, we will not have enough closure to apply Theorem 4.6. However, noting that
$\operatorname {\mathrm {cf}}(\delta _{k+1}) = \delta ^+$
, we will not have enough closure to apply Theorem 4.6. However, noting that
![]() $|\mathbb {L}_{s_\delta }|< \kappa _1$
, we can instead apply Theorem 3.14 to select
$|\mathbb {L}_{s_\delta }|< \kappa _1$
, we can instead apply Theorem 3.14 to select
![]() $\delta _k$
such that in the extension of
$\delta _k$
such that in the extension of
![]() $V[H]$
by
$V[H]$
by
![]() $\mathbb {L}_{s_{\delta _k}}$
, the strong tree property holds at
$\mathbb {L}_{s_{\delta _k}}$
, the strong tree property holds at
![]() $(\nu _s^k)^+$
.
$(\nu _s^k)^+$
.
We repeat this argument for
![]() $k=0$
. Let
$k=0$
. Let
![]() $\nu $
be the limit of
$\nu $
be the limit of
![]() $\langle \kappa _\rho \mid \rho <\omega _{\alpha _0}\rangle $
. By the previous stages in our construction, for each
$\langle \kappa _\rho \mid \rho <\omega _{\alpha _0}\rangle $
. By the previous stages in our construction, for each
![]() $\mu $
in the projection of
$\mu $
in the projection of
![]() $\operatorname {\mathrm {Index}}$
to the first coordinate, we have built a sequence
$\operatorname {\mathrm {Index}}$
to the first coordinate, we have built a sequence
![]() $s_\mu = \mu ^\smallfrown \langle \delta _i^\mu \mid 0 < i \leq n\rangle $
in
$s_\mu = \mu ^\smallfrown \langle \delta _i^\mu \mid 0 < i \leq n\rangle $
in
![]() $\operatorname {\mathrm {Index}}$
such that in the extension of
$\operatorname {\mathrm {Index}}$
such that in the extension of
![]() $V[H]$
by
$V[H]$
by
![]() $\mathbb {L}_{s_\mu }$
,
$\mathbb {L}_{s_\mu }$
,
![]() $\operatorname {\mathrm {ITP}}$
or the strong tree property holds at
$\operatorname {\mathrm {ITP}}$
or the strong tree property holds at
![]() $\nu _{s_\mu }^i$
for all
$\nu _{s_\mu }^i$
for all
![]() $i> 0$
. If
$i> 0$
. If
![]() $\operatorname {\mathrm {cf}}(\delta _1^\mu )> \mu ^+$
, then setting
$\operatorname {\mathrm {cf}}(\delta _1^\mu )> \mu ^+$
, then setting
![]() $\mathbb {L}_{s_\mu }^0 = \operatorname {\mathrm {Col}}(\omega _{\alpha _0}, \delta _0)$
and
$\mathbb {L}_{s_\mu }^0 = \operatorname {\mathrm {Col}}(\omega _{\alpha _0}, \delta _0)$
and
![]() $\mathbb {L}_{s_\mu }^1$
to be the remainder of the forcing, we can apply Theorem 4.6 to obtain some
$\mathbb {L}_{s_\mu }^1$
to be the remainder of the forcing, we can apply Theorem 4.6 to obtain some
![]() $\mu $
such that after forcing with
$\mu $
such that after forcing with
![]() $\mathbb {L}_{s_\mu },$
ITP holds at
$\mathbb {L}_{s_\mu },$
ITP holds at
![]() $\nu ^+$
. If this is not the case, we can apply Theorem 3.14 to obtain the strong tree property at
$\nu ^+$
. If this is not the case, we can apply Theorem 3.14 to obtain the strong tree property at
![]() $\nu ^+$
. Let
$\nu ^+$
. Let
![]() $\delta _0 = \mu $
, and let
$\delta _0 = \mu $
, and let
![]() $s \mathrel {\mathop :}= s_\mu $
. By construction,
$s \mathrel {\mathop :}= s_\mu $
. By construction,
![]() $s \in \operatorname {\mathrm {Index}}$
such that in the extension of
$s \in \operatorname {\mathrm {Index}}$
such that in the extension of
![]() $V[H]$
by
$V[H]$
by
![]() $\mathbb {L}_s$
, ITP or the strong tree property hold at
$\mathbb {L}_s$
, ITP or the strong tree property hold at
![]() $\nu _i^+$
for all
$\nu _i^+$
for all
![]() $i \leq n$
.
$i \leq n$
.
Finally, we examine the cardinal structure in this extension. The first chosen cardinal
![]() $\delta _0$
is collapsed to
$\delta _0$
is collapsed to
![]() $\omega _{\alpha _0}$
, while
$\omega _{\alpha _0}$
, while
![]() $\delta _1$
is collapsed to
$\delta _1$
is collapsed to
![]() $\delta _0^{+f(1)} = \omega _{\alpha _0}^{+f(1)} = \omega _{\alpha _1}$
. Working inductively we see that each
$\delta _0^{+f(1)} = \omega _{\alpha _0}^{+f(1)} = \omega _{\alpha _1}$
. Working inductively we see that each
![]() $\delta _i$
is collapsed to
$\delta _i$
is collapsed to
![]() $\omega _{\alpha _{i}}$
. The cardinals between each successive
$\omega _{\alpha _{i}}$
. The cardinals between each successive
![]() $\kappa _\rho $
are collapsed, and
$\kappa _\rho $
are collapsed, and
![]() $\kappa _0$
will become
$\kappa _0$
will become
![]() $\omega _{\alpha _n}^{+3}$
. It follows that each
$\omega _{\alpha _n}^{+3}$
. It follows that each
![]() $\nu _i$
becomes
$\nu _i$
becomes
![]() $\kappa _0^{+\omega _{\alpha _i}} = \aleph _{\omega _{\alpha _i}}$
.
$\kappa _0^{+\omega _{\alpha _i}} = \aleph _{\omega _{\alpha _i}}$
.
We conclude that, in the extension of
![]() $V[H]$
by
$V[H]$
by
![]() $\mathbb {L}_s$
, the strong tree property holds at
$\mathbb {L}_s$
, the strong tree property holds at
![]() $\aleph _{\omega _{\alpha _i}+1}$
for all
$\aleph _{\omega _{\alpha _i}+1}$
for all
![]() $i \leq n$
, and if
$i \leq n$
, and if
![]() $\alpha _{i+1}> \alpha _i+1$
, ITP holds at
$\alpha _{i+1}> \alpha _i+1$
, ITP holds at
![]() $\aleph _{\omega _{\alpha _i}+1}$
.
$\aleph _{\omega _{\alpha _i}+1}$
.
7. Open problems
The natural question is, of course, can we get ITP at
![]() $\aleph _{\omega +1}$
along with ITP at every
$\aleph _{\omega +1}$
along with ITP at every
![]() $\aleph _n$
? As we have shown, the difficulty is at
$\aleph _n$
? As we have shown, the difficulty is at
![]() $n = 2$
and
$n = 2$
and
![]() $n=3$
.
$n=3$
.
Question 7.1. Can we obtain ITP at
![]() $\aleph _{\omega +1}$
and at
$\aleph _{\omega +1}$
and at
![]() $\aleph _2$
simultaneously? What about at
$\aleph _2$
simultaneously? What about at
![]() $\aleph _{\omega +1}$
along with
$\aleph _{\omega +1}$
along with
![]() $\aleph _n$
for all
$\aleph _n$
for all
![]() $2 \leq n < \omega ?$
$2 \leq n < \omega ?$
Another more ambitious project is obtaining the tree property, or more optimistically its generalizations, up to
![]() $\aleph _{\omega _1+1}$
. There are two major obstacles. First, we would need to obtain the tree property at the successor of every cardinal with countable cofinality. Golshani and Hayut have shown in [Reference Golshani and Hayut7] that this can be done for any countable initial segment of these cardinals. (Using the lemmas in this paper, their argument immediately generalizes to the one-cardinal version of ITP, but not to the full two-cardinal property.)
$\aleph _{\omega _1+1}$
. There are two major obstacles. First, we would need to obtain the tree property at the successor of every cardinal with countable cofinality. Golshani and Hayut have shown in [Reference Golshani and Hayut7] that this can be done for any countable initial segment of these cardinals. (Using the lemmas in this paper, their argument immediately generalizes to the one-cardinal version of ITP, but not to the full two-cardinal property.)
Question 7.2. Can we obtain the tree property
![]() $($
or ITP
$($
or ITP
![]() $)$
at every successor of a singular cardinal below
$)$
at every successor of a singular cardinal below
![]() $\aleph _{\omega _1}$
?
$\aleph _{\omega _1}$
?
The other obstacle comes from the reflection principles used to obtain the tree property at the successor of a singular cardinal. To obtain the tree property at
![]() $\aleph _{\omega _1+1}$
,
$\aleph _{\omega _1+1}$
,
![]() $\aleph _2$
in the final model will be
$\aleph _2$
in the final model will be
![]() $\mu ^+$
, where
$\mu ^+$
, where
![]() $\mu $
is the chosen cardinal that is collapsed to
$\mu $
is the chosen cardinal that is collapsed to
![]() $\omega _1$
. To obtain the tree property at
$\omega _1$
. To obtain the tree property at
![]() $\aleph _2$
using standard techniques, however,
$\aleph _2$
using standard techniques, however,
![]() $\aleph _2$
must be generically supercompact.
$\aleph _2$
must be generically supercompact.
Question 7.3. Can we obtain the tree property at
![]() $\aleph _2$
and at
$\aleph _2$
and at
![]() $\aleph _{\omega _1+1}$
simultaneously? What about the strong tree property or ITP?
$\aleph _{\omega _1+1}$
simultaneously? What about the strong tree property or ITP?
Finally, while we have shown that it is consistent for ITP to hold simultaneously at the successors of small singular cardinals with different cofinalities, our argument is limited to finitely many cofinalities.
Question 7.4. Given a sequence
![]() $\langle \gamma _n \mid n < \omega \rangle $
of regular cardinals, can we obtain the strong tree property
$\langle \gamma _n \mid n < \omega \rangle $
of regular cardinals, can we obtain the strong tree property
![]() $($
or ITP
$($
or ITP
![]() $)$
at
$)$
at
![]() $\aleph _{\gamma _n+1}$
for all n simultaneously?
$\aleph _{\gamma _n+1}$
for all n simultaneously?