Table of contents
Table of contents
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. iii-iv
-
- Article
- Export citation
Research Article
Algebraic completeness results for R-mingle and its extensions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-13
-
- Article
- Export citation
Hierarchies of Boolean algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 365-374
-
- Article
- Export citation
On initial segments of hyperdegrees1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 189-197
-
- Article
- Export citation
Correction
Errata
-
- Published online by Cambridge University Press:
- 12 March 2014, p. v
-
- Article
- Export citation
Research Article
The number of countable models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 14-18
-
- Article
- Export citation
The strong homogeneity conjecture
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 375-377
-
- Article
- Export citation
On analytic well-orderings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 198-204
-
- Article
- Export citation
Many-valued logics of extended Gentzen style II
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 493-528
-
- Article
- Export citation
Axiomatizable theories with few axiomatizable extensions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 205-209
-
- Article
- Export citation
On an algebra of sets of finite sequences 1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 19-28
-
- Article
- Export citation
A coding theorem for isols
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 378-382
-
- Article
- Export citation
The decision problem for formulas in prenex conjunctive normal form with binary disjunctions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 210-216
-
- Article
- Export citation
An embedding of classical logic in S4
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 529-534
-
- Article
- Export citation
Turing degrees and many-one degrees of maximal sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 29-40
-
- Article
- Export citation
A cornucopia of minimal degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 383-388
-
- Article
- Export citation
A model theoretic characterization of effective operations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 217-222
-
- Article
- Export citation
Finite partially-ordered quantification
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 535-555
-
- Article
- Export citation
Admissible ordinals and intrinsic consistency
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 389-400
-
- Article
- Export citation
A theorem on initial segments of degrees 1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 41-45
-
- Article
- Export citation



 nonisomorphic countable models. It has been conjected (e.g., in [4]) that if it has an uncountable number of such models then it has exactly
nonisomorphic countable models. It has been conjected (e.g., in [4]) that if it has an uncountable number of such models then it has exactly  well-orderings have been investigated by many authors. Now we shall generally consider analytic well-orderings and compare their representation-capacities for ordinals.
well-orderings have been investigated by many authors. Now we shall generally consider analytic well-orderings and compare their representation-capacities for ordinals.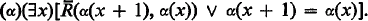 .
.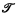 in standard formalization such that all axiomatizable extensions
in standard formalization such that all axiomatizable extensions 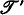 of
of 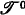 ,
,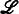 be an ℒ-structure. We assume that ℒ has a simple infinite sequence
be an ℒ-structure. We assume that ℒ has a simple infinite sequence 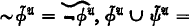
 cylindrifications
cylindrifications 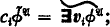 diagonal elements (0-ary operations)
diagonal elements (0-ary operations) 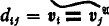 . In this way we make the class of all sets
. In this way we make the class of all sets 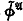 of all cylindric set algebras (of dimension
of all cylindric set algebras (of dimension 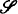 be the class of all algebras of sets of finite sequences (an exact definition is given in §1).
be the class of all algebras of sets of finite sequences (an exact definition is given in §1).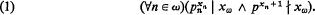
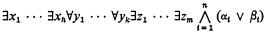
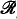 /
/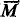 obtained from the recursive functions of one variable under the equivalence relation
obtained from the recursive functions of one variable under the equivalence relation 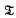 be a standard formalization of type theory. In [6] Kreisel introduced
be a standard formalization of type theory. In [6] Kreisel introduced