In [1] it is shown that for every sequence x = 〈xn : n ∈ ω〉 ∈ Xω Λ there is an isol xω (essentially an immunized product) such that

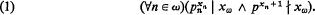
Here we have used the notation: Λ = the isols, ω = the nonnegative integers, pn is the nth prime rational integer starting with p0 = 2, ∣ denotes divisibility and ∤ its negation. If p is an arbitrary prime, py ∣ x, pz ∣ x, and y < z then py+1 ∣ x. In particular since y ∈ ω is comparable with every element of Λ, the conditions py ∣ x and py+1 ∤ x uniquely determine y. Thus every sequence x ∈ Xωω is uniquely determined by an xω satisfying (1) and consequently may be used as a “code” for that sequence. In Theorem 1 it is shown that (1) does not uniquely determine the values of an arbitrary sequence x ∈ XωΛ, however in Theorem 3 we find a different scheme which does. At the very end of the paper we give some reasons why coding theorems are useful. It should also be mentioned that for a coding theorem to be meaningful it is necessary to restrict the operations by which a sequence can be recaptured from its code. Otherwise a triviality results. Our coding theorem will allow all operations which are first order definable in Λ with respect to addition, multiplication, and exponentiation. We conjecture that the latter operation is really necessary.