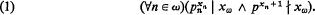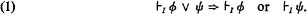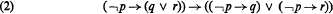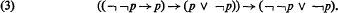Research Article
Hierarchies of Boolean algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 365-374
-
- Article
- Export citation
The strong homogeneity conjecture
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 375-377
-
- Article
- Export citation
A coding theorem for isols
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 378-382
-
- Article
- Export citation
A cornucopia of minimal degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 383-388
-
- Article
- Export citation
Admissible ordinals and intrinsic consistency
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 389-400
-
- Article
- Export citation
Construction of models for algebraically generalized recursive function theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 401-409
-
- Article
- Export citation
Strong partition properties for infinite cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 410-428
-
- Article
- Export citation
A note on the hyperarithmetical hierarchy
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 429-430
-
- Article
- Export citation
The decidability of the Kreisel-Putnam system1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 431-437
-
- Article
- Export citation
Reviews
Reviews - Stephen Cole Kleene. Mathematical logic. John Wiley & Sons, Inc., New York, London, and Sydney, 1967, xiii + 398 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 438-440
-
- Article
- Export citation
Hans Hermes. Eine Termlogik mit Auswahloperator. Lecture notes in mathematics no. 6, Springer-Verlag, Berlin, Heidelberg, and New York, 1965, iv + 42 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 440
-
- Article
- Export citation
Ladislav Rieger. Zu den Strukturen der klassischen Prädikatenlogik. Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 10 (1964), pp. 121–138. - Ladislav Rieger. Algebraic methods of mathematical logic. Translated from the Czech by Michal Basch. Academia Publishing House of the Czechoslovak Academy of Sciences, Prague, and Academic Press, New York and London, 1967, 210 pp. - M. Katětov. Preface. Therein, pp. 5–6.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 440-441
-
- Article
- Export citation
Tadeusz Kotarbiński. Introduction. Notes on the development of formal logic in Poland in the years 1900–39. Polish logic 1920–1939, edited by Storrs McCall. The Clarendon Press, Oxford1967, pp. 1–14. - Jan Łukasiewicz. On the notion of possibility. English translation of the first half of 1864 by H. Hiż. Polish logic 1920–1939, edited by Storrs McCall. The Clarendon Press, Oxford1967, pp. 15–16. - Jan Łukasiewicz. On three-valued logic. English translation of the second half of 1864 by H. Hiż. Polish logic 1920–1939, edited by Storrs McCall. The Clarendon Press, Oxford1967, pp. 16–18. - Jan Łukasiewicz. On determinism. English translation of XXXIII 130 by Z. Jordan. Polish logic 1920–1939, edited by Storrs McCall. The Clarendon Press, Oxford1967, pp. 19–39. - Jan Łukasiewicz. Philosophical remarks on many-valued systems of propositional logic. English translation of 1868 by H. Weber. Polish logic 1920–1939, edited by Storrs McCall. The Clarendon Press, Oxford1967, pp. 40–65. - Jan Łukasiewicz. On the history of the logic of propositions. English translation of 18613 by S. McCall. Polish logic 1920–1939, edited by Storrs McCall. The Clarendon Press, Oxford1967, pp. 66–87. - Jan Łukasiewicz. The equivalential calculus. English translation of VI115 by P. Woodruff. Polish logic 1920–1939, edited by Storrs McCall. The Clarendon Press, Oxford1967, pp. 88–115. - Stanisław Leśniewski. Introductory remarks to the continuation of my article: ‘Grundzüge eines neuen Systems der Grundlagen der Mathematik.’ English translation of V 83 by W. Teichmann and S. McCall. Polish logic 1920–1939, edited by Storrs McCall. The Clarendon Press, Oxford1967, pp. 116–169. - Stanisław Leśniewski. On definitions in the so-called theory of deduction. English translation of 20213 by E. C. Luschei. Polish logic 1920–1939, edited by Storrs McCall. The Clarendon Press, Oxford1967, pp. 170–187. - Bolesław Sobociński. Successive simplifications of the axiom-system of Leiniewski's ontology. English translation of 4432 by Z. Jordan. Polish logic 1920–1939, edited by Storrs McCall. The Clarendon Press, Oxford1967, pp. 188–200.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 442-446
-
- Article
- Export citation
Rosaria Egidi. Ontologia e conoscenza matematica. Un saggio su Gottlob Frege. Publicazioni dell'Istituto di Filosofia dell'Università di Roma, no. X. G. C. Sansoni Editore, Florence1963, 274 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 446-447
-
- Article
- Export citation
David Wiggins. Identity and spatio-temporal continuity. Basil Blackwell, Oxford1967, viii + 83 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 447-448
-
- Article
- Export citation
G. B. Keene. The relational syllogism. A systematic approach to relational logic. University of Exeter, Exeter1969, iv + 35 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 448-450
-
- Article
- Export citation
William of Sherwood. Treatise on syncategorematic words. Translated with an introduction and notes by Norman Kretzmann. University of Minnesota Press, Minneapolis1968, xvii + 173 pp. - Norman Kretzmann. Preface. Therein, pp. v–vii. - Norman Kretzmann. Translator's introduction. Therein, pp. 3–9.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 450-451
-
- Article
- Export citation
Marguerite H. Foster and Michael L. Martin. General introduction. Probability, confirmation, and simplicity. Readings in the philosophy of inductive logic. Edited by Marguerite H. Foster and Michael L. Martin. The Odyssey Press Inc., New York1966, pp. 1–13. - Marguerite H. Foster and Michael L. Martin. The meaning of probability. Introduction. Probability, confirmation, and simplicity. Readings in the philosophy of inductive logic. Edited by Marguerite H. Foster and Michael L. Martin. The Odyssey Press Inc., New York1966, pp. 17–26. - Rudolf Carnap. On inductive logic. A reprint of XI19. Probability, confirmation, and simplicity. Readings in the philosophy of inductive logic. Edited by Marguerite H. Foster and Michael L. Martin. The Odyssey Press Inc., New York1966, pp. 35–61. - Stephen F. Barker. Enumerative induction. A reprint of pp. 82–90 of XXVII 122. Probability, confirmation, and simplicity. Readings in the philosophy of inductive logic. Edited by Marguerite H. Foster and Michael L. Martin. The Odyssey Press Inc., New York1966, pp. 61–66. - Alfred J. Ayer. The conception of probability as a logical relation. A reprint of XXXI 145. Probability, confirmation, and simplicity. Readings in the philosophy of inductive logic. Edited by Marguerite H. Foster and Michael L. Martin. The Odyssey Press Inc., New York1966, pp. 67–73. - John W. Lenz. Carnap on defining “degree of confirmation. “Probability, confirmation, and simplicity. Readings in the philosophy of inductive logic. Edited by Marguerite H. Foster and Michael L. Martin. The Odyssey Press Inc., New York1966, pp. 73–79. (Reprinted from Philosophy of science, vol. 23 (1956), pp. 230–236.) - Hans Reichenbach. The frequency interpretation. A reprint of pp. 68–69, 372–383, and 434–442 of XVI 48. Probability, confirmation, and simplicity. Readings in the philosophy of inductive logic. Edited by Marguerite H. Foster and Michael L. Martin. The Odyssey Press Inc., New York1966, pp. 80–99. - Marguerite H. Foster and Michael L. Martin. Problems of confirmation theory. Introduction. Probability, confirmation, and simplicity. Readings in the philosophy of inductive logic. Edited by Marguerite H. Foster and Michael L. Martin. The Odyssey Press Inc., New York1966, pp. 131–137. - Rudolf Carnap. Truth and confirmation. A reprint of XVII 139. Probability, confirmation, and simplicity. Readings in the philosophy of inductive logic. Edited by Marguerite H. Foster and Michael L. Martin. The Odyssey Press Inc., New York1966, pp. 137–144. - Carl G. Hempel. Studies in the logic of confirmation. A reprint of X 104. Probability, confirmation, and simplicity. Readings in the philosophy of inductive logic. Edited by Marguerite H. Foster and Michael L. Martin. The Odyssey Press Inc., New York1966, pp. 145–183.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 451-454
-
- Article
- Export citation
Jaakko Hintikka. Towards a theory of inductive generalization. Logic, methodology and philosophy of science, Proceedings of the 1964 International Congress, edited by Yehoshua Bar-Hillel, Studies in logic and the foundations of mathematics, North-Holland Publishing Company, Amsterdam1965, pp. 274–288.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 454
-
- Article
- Export citation
Jaakko Hintikka. On a combined system of inductive logic. Studia logico-mathematica et philosophica, in honorem Rolf Nevanlinna die natali eius septuagesimo 22. X. 1965. Acta philosophica Fennica, no. 18 (1965), pp. 21–30.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 454-455
-
- Article
- Export citation