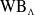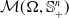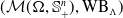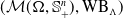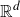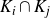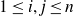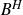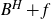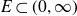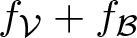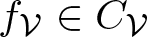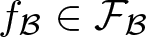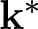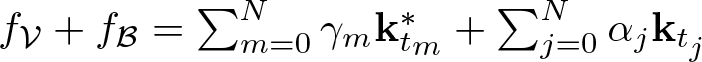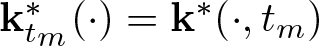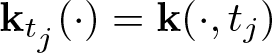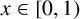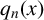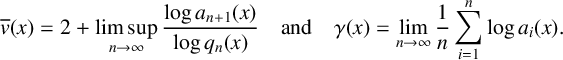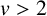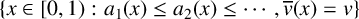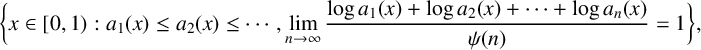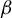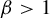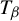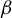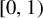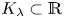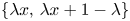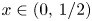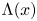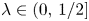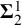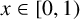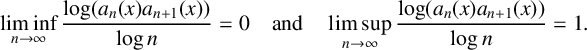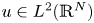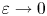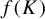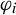329 results in 28Axx
On a general matrix-valued unbalanced optimal transport problem
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The connectedness of Sierpiński sponges with rotational and reflectional components and associated graph-directed systems
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 21 February 2025, pp. 1-24
-
- Article
- Export citation
Fractional Brownian motion with deterministic drift: how critical is drift regularity in hitting probabilities
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 February 2025, pp. 103-132
- Print publication:
- January 2025
-
- Article
- Export citation
The dimension of the feasible region of pattern densities
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-14
- Print publication:
- January 2025
-
- Article
- Export citation
Birkhoff spectrum for diagonally self-affine sets and digit frequencies for GLS systems with redundancy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fractal interpolant curve fitting and reproducing kernel Hilbert spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 247-267
-
- Article
-
- You have access
- HTML
- Export citation
THE MULTIFRACTAL SPECTRUM OF CONTINUED FRACTIONS WITH NONDECREASING PARTIAL QUOTIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-13
-
- Article
-
- You have access
- HTML
- Export citation
Shrinking parallelepiped targets for
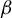 $\beta $-dynamical systems
$\beta $-dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 19 November 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
Exact dimension functions of the prime continued fraction Cantor set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 14 November 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOREL LINE GRAPHS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 November 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasisymmetrically rigid self-similar carpets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 22 October 2024, pp. 1-14
-
- Article
-
- You have access
- HTML
- Export citation
Uniform Diophantine approximation and run-length function in continued fractions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1246-1280
- Print publication:
- April 2025
-
- Article
-
- You have access
- HTML
- Export citation
On a class of self-similar sets which contain finitely many common points
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
A reproducing kernel approach to Lebesgue decomposition
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON HOMOMORPHISM GRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 May 2024, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-invertible planar self-affine sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 08 May 2024, pp. 49-65
- Print publication:
- July 2024
-
- Article
-
- You have access
- HTML
- Export citation
Weighted topological pressure revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 08 May 2024, pp. 34-70
- Print publication:
- January 2025
-
- Article
-
- You have access
- HTML
- Export citation
ASYMPTOTIC BEHAVIOUR FOR PRODUCTS OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 18 April 2024, pp. 448-459
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Sharp conditions for the validity of the Bourgain–Brezis–Mironescu formula
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-24
-
- Article
-
- You have access
- HTML
- Export citation
On a self-embedding problem for self-similar sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 14 February 2024, pp. 3002-3011
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation