No CrossRef data available.
Article contents
On a class of self-similar sets which contain finitely many common points
Published online by Cambridge University Press: 30 May 2024
Abstract
For $\lambda \in (0,\,1/2]$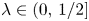 let $K_\lambda \subset \mathbb {R}$
let $K_\lambda \subset \mathbb {R}$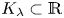 be a self-similar set generated by the iterated function system $\{\lambda x,\, \lambda x+1-\lambda \}$
be a self-similar set generated by the iterated function system $\{\lambda x,\, \lambda x+1-\lambda \}$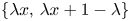 . Given $x\in (0,\,1/2)$
. Given $x\in (0,\,1/2)$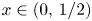 , let $\Lambda (x)$
, let $\Lambda (x)$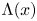 be the set of $\lambda \in (0,\,1/2]$
be the set of $\lambda \in (0,\,1/2]$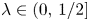 such that $x\in K_\lambda$
such that $x\in K_\lambda$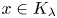 . In this paper we show that $\Lambda (x)$
. In this paper we show that $\Lambda (x)$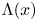 is a topological Cantor set having zero Lebesgue measure and full Hausdorff dimension. Furthermore, we show that for any $y_1,\,\ldots,\, y_p\in (0,\,1/2)$
is a topological Cantor set having zero Lebesgue measure and full Hausdorff dimension. Furthermore, we show that for any $y_1,\,\ldots,\, y_p\in (0,\,1/2)$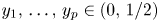 there exists a full Hausdorff dimensional set of $\lambda \in (0,\,1/2]$
there exists a full Hausdorff dimensional set of $\lambda \in (0,\,1/2]$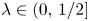 such that $y_1,\,\ldots,\, y_p \in K_\lambda$
such that $y_1,\,\ldots,\, y_p \in K_\lambda$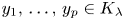 .
.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh





