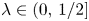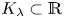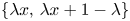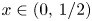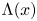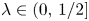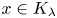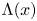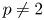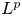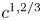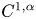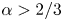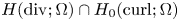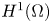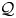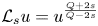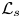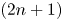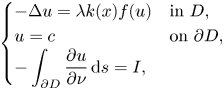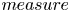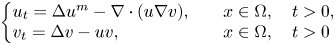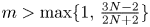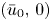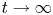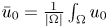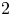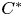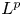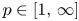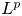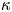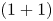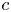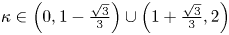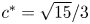FirstView articles
Research Article
Rigidity for the perimeter inequality under Schwarz symmetrization
- Part of:
-
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Addendum
The homotopy decomposition of the suspension of a non-simply-connected five-manifold – ADDENDUM
-
- Published online by Cambridge University Press:
- 30 May 2024, p. 1
-
- Article
- Export citation
Research Article
On a class of self-similar sets which contain finitely many common points
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1-22
-
- Article
- Export citation
Distribution in homology classes and discrete fractal dimension
- Part of:
-
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lp positivity preservation and self-adjointness of Schrödinger operators on incomplete Riemannian manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral asymptotics for linear elasticity: the case of mixed boundary conditions
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a localization-in-frequency approach for a class of elliptic problems with singular boundary data
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2024, pp. 1-35
-
- Article
- Export citation
The geometry of C1,α flat isometric immersions
- Part of:
-
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A global higher regularity result for the static relaxed micromorphic model on smooth domains
- Part of:
-
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-15
-
- Article
- Export citation
Asymptotic profiles of a nonlocal dispersal SIS epidemic model with saturated incidence
- Part of:
-
- Published online by Cambridge University Press:
- 14 May 2024, pp. 1-33
-
- Article
- Export citation
Flat model structures and Gorenstein objects in functor categories
- Part of:
-
- Published online by Cambridge University Press:
- 14 May 2024, pp. 1-21
-
- Article
- Export citation
Optimal decay for solutions of nonlocal semilinear equations with critical exponent in homogeneous groups
- Part of:
-
- Published online by Cambridge University Press:
- 14 May 2024, pp. 1-29
-
- Article
- Export citation
Catenaries and minimal surfaces of revolution in hyperbolic space
- Part of:
-
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On conformally flat minimal Legendrian submanifolds in the unit sphere
- Part of:
-
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-30
-
- Article
- Export citation
Desingularization of 2D elliptic free-boundary problem with non-autonomous nonlinearity
- Part of:
-
- Published online by Cambridge University Press:
- 30 April 2024, pp. 1-38
-
- Article
- Export citation
Global boundedness and large time behaviour in a higher-dimensional quasilinear chemotaxis system with consumption of chemoattractant
- Part of:
-
- Published online by Cambridge University Press:
- 30 April 2024, pp. 1-26
-
- Article
- Export citation
Spreading primitive groups of diagonal type do not exist
-
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topologically free actions and ideals in twisted Banach algebra crossed products
- Part of:
-
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1-31
-
- Article
- Export citation
Bifurcation of the travelling wave solutions in a perturbed (1 + 1)-dimensional dispersive long wave equation via a geometric approach
- Part of:
-
- Published online by Cambridge University Press:
- 25 April 2024, pp. 1-28
-
- Article
- Export citation
Singer conjecture for varieties with semismall Albanese map and residually finite fundamental group
- Part of:
-
- Published online by Cambridge University Press:
- 19 April 2024, pp. 1-7
-
- Article
- Export citation