Hostname: page-component-848d4c4894-2xdlg Total loading time: 0 Render date: 2024-06-15T11:55:33.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Flat model structures and Gorenstein objects in functor categories

Part of: General theory of categories and functors Homological algebra

Published online by Cambridge University Press:  14 May 2024

Zhenxing Di ,
Liping Li ,
Li Liang  and
Yajun Ma
Zhenxing Di
Affiliation:
School of Mathematical Sciences, Huaqiao University, Quanzhou 362021, China (dizhenxing@163.com)
Liping Li
Affiliation:
Department of Mathematics, Hunan Normal University, Changsha 410081, China (lipingli@hunnu.edu.cn)
Li Liang
Affiliation:
Department of Mathematics, Lanzhou Jiaotong University, Lanzhou 730070, China Gansu Provincial Research Center for Basic Disciplines of Mathematics and Statistics, Lanzhou 730070, China (lliangnju@gmail.com); https://sites.google.com/site/lliangnju
Yajun Ma
Affiliation:
Department of Mathematics, Lanzhou Jiaotong University, Lanzhou 730070, China (13919042158@163.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct a flat model structure on the category ${_{\mathcal {Q},\,R}\mathsf {Mod}}$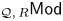 of additive functors from a small preadditive category $\mathcal {Q}$ satisfying certain conditions to the module category ${_{R}\mathsf {Mod}}$ over an associative ring $R$, whose homotopy category is the $\mathcal {Q}$-shaped derived category introduced by Holm and Jørgensen. Moreover, we prove that for an arbitrary associative ring $R$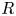, an object in ${_{\mathcal {Q},\,R}\mathsf {Mod}}$ is Gorenstein projective (resp., Gorenstein injective, Gorenstein flat, projective coresolving Gorenstein flat) if and only if so is its value on each object of $\mathcal {Q}$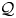, and hence improve a result by Dell'Ambrogio, Stevenson and Šťovíček.

Keywords

Gorenstein objectabelian model structurefunctor category

MSC classification

Primary: 18G25: Relative homological algebra, projective classes
Secondary: 18A25: Functor categories, comma categories
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 21
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avramov, L. L. and Foxby, H.-B.. Homological dimensions of unbounded complexes. J. Pure Appl. Algebra 71 (1991), 129–155.CrossRefGoogle Scholar
Chen, X.-W. and Ren, W.. Frobenius functors and Gorenstein homological properties. J. Algebra 610 (2022), 18–37.CrossRefGoogle Scholar
Crawley-Boevey, W.. Locally finitely presented additive categories. Comm. Algebra 22 (1994), 1641–1674.CrossRefGoogle Scholar
Dell'Ambrogio, I., Stevenson, G. and Šťovíček, J.. Gorenstein homological algebra and universal coefficient theorems. Math. Z. 287 (2017), 1109–1155.CrossRefGoogle Scholar
Enochs, E. E., Estrada, S. and García Rozas, J. R.. Gorenstein categories and Tate cohomology on projective schemes. Math. Nachr. 281 (2008), 525–540.CrossRefGoogle Scholar
Enochs, E. E. and García Rozas, J. R.. Gorenstein injective and projective complexes. Comm. Algebra 26 (1998), 1657–1674.CrossRefGoogle Scholar
Enochs, E. E. and Jenda, O. M. G., Relative homological algebra, de Gruyter Expositions in Mathematics, Vol. 30 (Walter de Gruyter & Co., Berlin, 2000).CrossRefGoogle Scholar
Gillespie, J.. The flat model structure on ${\rm Ch}(R)$. Trans. Amer. Math. Soc. 356 (2004), 3369–3390.CrossRefGoogle Scholar
Gillespie, J.. How to construct a Hovey triple from two cotorsion pairs. Fund. Math. 230 (2015), 281–289.CrossRefGoogle Scholar
Gillespie, J.. Gorenstein complexes and recollements from cotorsion pairs. Adv. Math. 291 (2016), 859–911.CrossRefGoogle Scholar
Göbel, R. and Trlifaj, J., Approximations and endomorphism algebras of modules. Volume 2, extended ed., De Gruyter Expositions in Mathematics, Vol. 41 (Walter de Gruyter GmbH & Co. KG, Berlin, 2012), Predictions.CrossRefGoogle Scholar
Holm, H. and Jørgensen, P.. Cotorsion pairs in categories of quiver representations. Kyoto J. Math. 59 (2019), 575–606.CrossRefGoogle Scholar
Holm, H. and Jørgensen, P.. Model categories of quiver representations. Adv. Math. 357 (2019), 106826.CrossRefGoogle Scholar
Holm, H. and Jørgensen, P.. The $Q$-shaped derived category of a ring. J. Lond. Math. Soc. (2) 106 (2022), 3263–3316.CrossRefGoogle Scholar
Holm, H. and Jørgensen, P., The $Q$-shaped derived category of a ring—compact and perfect objects, Trans. Amer. Math. Soc., to appear, available at arxiv:2208.13282 [math.RT].Google Scholar
Hovey, M., Model categories, Mathematical Surveys and Monographs, Vol. 63 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Hovey, M.. Cotorsion pairs, model category structures, and representation theory. Math. Z. 241 (2002), 553–592.CrossRefGoogle Scholar
Liu, Z. and Zhang, C.. Gorenstein injective complexes of modules over Noetherian rings. J. Algebra 321 (2009), 1546–1554.Google Scholar
Oberst, U. and Röhrl, H.. Flat and coherent functors. J. Algebra 14 (1970), 91–105.CrossRefGoogle Scholar
Quillen, D. G., Homotopical algebra, Lecture Notes in Mathematics, No. 43 (Springer-Verlag, Berlin-New York, 1967).CrossRefGoogle Scholar
Rump, W.. Flat covers in abelian and in non-abelian categories. Adv. Math. 225 (2010), 1589–1615.CrossRefGoogle Scholar
Šaroch, J. and Št'ovíček, J.. Singular compactness and definability for $\Sigma$-cotorsion and Gorenstein modules. Selecta Math. (N.S.) 26 (2020), 23.CrossRefGoogle Scholar
Yang, X. and Liu, Z.. Gorenstein projective, injective, and flat complexes. Comm. Algebra 39 (2011), 1705–1721.CrossRefGoogle Scholar