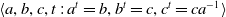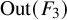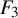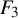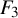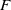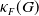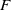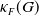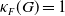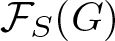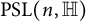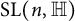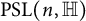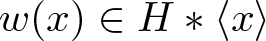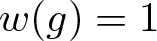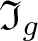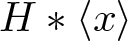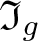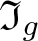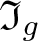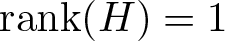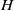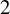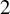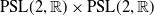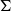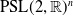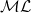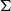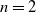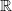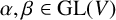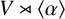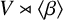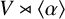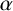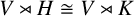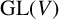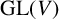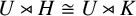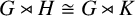330 results in 20Exx
A hyperbolic free-by-cyclic group determined by its finite quotients
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 04 April 2025, pp. 1-3
-
- Article
- Export citation
Tree-like graphings, wallings, and median graphings of equivalence relations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 March 2025, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Shelah group in ZFC
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 March 2025, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linearity of compact R-analytic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 March 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The conjugacy problem for
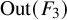 $\operatorname {Out}(F_3)$
$\operatorname {Out}(F_3)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 February 2025, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal linear sofic approximations of countable groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 24 January 2025, pp. 245-268
- Print publication:
- May 2025
-
- Article
- Export citation
Conditions for the supersolvability of
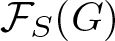 $\mathcal{F}_{S}(G)$
$\mathcal{F}_{S}(G)$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 23 January 2025, pp. 1-7
-
- Article
- Export citation
A characterization of virtually free groups among hyperbolic groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 13 January 2025, pp. 1-7
-
- Article
- Export citation
Presentation of an Iwasawa algebra: The pro-p Iwahori of simple, simply connected, split groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-18
-
- Article
- Export citation
Product of two involutions in quaternionic special linear group
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 08 January 2025, pp. 1-19
-
- Article
- Export citation
Order-automorphism groups of Archimedean ordered groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-6
-
- Article
-
- You have access
- HTML
- Export citation
Ideals of equations for elements in a free group and Stallings folding
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 19 December 2024, pp. 1-42
-
- Article
-
- You have access
- HTML
- Export citation
A note on the splittings of finitely presented Bestvina–Brady groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 19 December 2024, pp. 224-227
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite presentability of twisted Brin–Thompson groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 December 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limit trees for free group automorphisms: universality
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e122
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fusion Systems and Rank
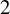 $2$ Simple Groups of Lie Type
$2$ Simple Groups of Lie Type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 November 2024, e102
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prosoluble subgroups of free profinite products
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 14 November 2024, e99
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cyclic orders and graphs of groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 21 October 2024, pp. 1125-1136
-
- Article
-
- You have access
- HTML
- Export citation
Weyl chamber length compactification of the
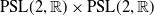 $\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$ maximal character variety
$\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$ maximal character variety
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 27 September 2024, pp. 11-33
- Print publication:
- January 2025
-
- Article
-
- You have access
- HTML
- Export citation
ISOMORPHISM OF RELATIVE HOLOMORPHS AND MATRIX SIMILARITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 23 September 2024, pp. 298-313
- Print publication:
- April 2025
-
- Article
-
- You have access
- HTML
- Export citation