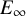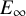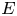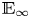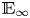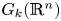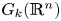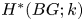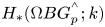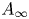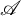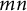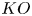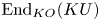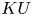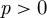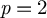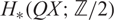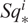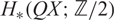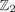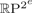29 results in 55Sxx
Equivariant parametrized topological complexity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-24
-
- Article
-
- You have access
- HTML
- Export citation
Adams’ cobar construction as a monoidal
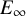 $E_{\infty }$-coalgebra model of the based loop space
$E_{\infty }$-coalgebra model of the based loop space
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 May 2024, e62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Obstruction theory and the level n elliptic genus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 03 August 2023, pp. 2000-2021
- Print publication:
- September 2023
-
- Article
- Export citation
Enough vector bundles on orbispaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 28 November 2022, pp. 2046-2081
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The affirmative answer to Singer's conjecture on the algebraic transfer of rank four
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 23 August 2022, pp. 1529-1542
- Print publication:
- October 2023
-
- Article
- Export citation
Corrigendum to “Topological complexity of real Grassmannians”
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 19 April 2022, pp. 1071-1072
- Print publication:
- June 2023
-
- Article
-
- You have access
- HTML
- Export citation
Principal bundles on two-dimensional CW-complexes with disconnected structure group
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 675-690
- Print publication:
- September 2022
-
- Article
- Export citation
Steenrod operators, the Coulomb branch and the Frobenius twist
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 04 November 2021, pp. 2494-2552
- Print publication:
- November 2021
-
- Article
- Export citation
Massey products in the homology of the loop space of a p-completed classifying space: finite groups with cyclic Sylow p-subgroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 30 September 2021, pp. 908-915
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Decomposition of topological Azumaya algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 506-524
- Print publication:
- June 2022
-
- Article
- Export citation
Brauer groups and Galois cohomology of commutative ring spectra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 1211-1264
- Print publication:
- June 2021
-
- Article
- Export citation
STEENROD OPERATIONS ON THE DE RHAM COHOMOLOGY OF ALGEBRAIC STACKS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 04 May 2021, pp. 493-540
- Print publication:
- March 2023
-
- Article
- Export citation
A HYDRODYNAMICAL HOMOTOPY CO-MOMENTUM MAP AND A MULTISYMPLECTIC INTERPRETATION OF HIGHER-ORDER LINKING NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 11 February 2021, pp. 335-354
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- Export citation
Topological complexity of real Grassmannians
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 12 January 2021, pp. 2013-2029
- Print publication:
- December 2021
-
- Article
- Export citation
ENHANCED FINITE TRIANGULATED CATEGORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 18 June 2020, pp. 741-783
- Print publication:
- May 2022
-
- Article
- Export citation
Realizing doubles: a conjugation zoo
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 April 2020, pp. 509-524
- Print publication:
- April 2021
-
- Article
- Export citation
A NOTE ON A-ANNIHILATED GENERATORS OF H*QX
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 21 March 2019, pp. 281-295
- Print publication:
- May 2020
-
- Article
- Export citation
Algebraic EHP Sequences Revisited
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 625-640
-
- Article
- Export citation
Four-fold Massey products in Galois cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 17 August 2018, pp. 1921-1959
- Print publication:
- September 2018
-
- Article
- Export citation
Symmetric Bi-Skew Maps and Symmetrized Motion Planning in Projective Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1087-1100
-
- Article
- Export citation