Article contents
Symmetric Bi-Skew Maps and Symmetrized Motion Planning in Projective Spaces
Published online by Cambridge University Press: 06 August 2018
Abstract
This work is motivated by the question of whether there are spaces X for which the Farber–Grant symmetric topological complexity TCS(X) differs from the Basabe–González–Rudyak–Tamaki symmetric topological complexity TCΣ(X). For a projective space 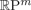 ${\open R}\hbox{P}^m$, it is known that
${\open R}\hbox{P}^m$, it is known that 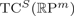 $\hbox{TC}^S ({\open R}\hbox{P}^{m})$ captures, with a few potential exceptional cases, the Euclidean embedding dimension of
$\hbox{TC}^S ({\open R}\hbox{P}^{m})$ captures, with a few potential exceptional cases, the Euclidean embedding dimension of 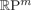 ${\open R}\hbox{P}^{m}$. We now show that, for all m≥1,
${\open R}\hbox{P}^{m}$. We now show that, for all m≥1, 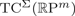 $\hbox{TC}^{\Sigma}({\open R}\hbox{P}^{m})$ is characterized as the smallest positive integer n for which there is a symmetric
$\hbox{TC}^{\Sigma}({\open R}\hbox{P}^{m})$ is characterized as the smallest positive integer n for which there is a symmetric 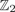 ${\open Z}_{2}$-biequivariant map Sm×Sm→Sn with a ‘monoidal’ behaviour on the diagonal. This result thus lies at the core of the efforts in the 1970s to characterize the embedding dimension of real projective spaces in terms of the existence of symmetric axial maps. Together with Nakaoka's description of the cohomology ring of symmetric squares, this allows us to compute both TC numbers in the case of
${\open Z}_{2}$-biequivariant map Sm×Sm→Sn with a ‘monoidal’ behaviour on the diagonal. This result thus lies at the core of the efforts in the 1970s to characterize the embedding dimension of real projective spaces in terms of the existence of symmetric axial maps. Together with Nakaoka's description of the cohomology ring of symmetric squares, this allows us to compute both TC numbers in the case of 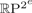 ${\open R}\hbox{P}^{2^{e}}$ for e≥1. In particular, this leaves the torus S1×S1 as the only closed surface whose symmetric (symmetrized) TCS (TCΣ) invariant is currently unknown.
${\open R}\hbox{P}^{2^{e}}$ for e≥1. In particular, this leaves the torus S1×S1 as the only closed surface whose symmetric (symmetrized) TCS (TCΣ) invariant is currently unknown.
Keywords
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 61 , Issue 4 , November 2018 , pp. 1087 - 1100
- Copyright
- Copyright © Edinburgh Mathematical Society 2018
References
- 1
- Cited by




