The past five years have witnessed an explosion in archaeological publications from all corners of the world employing Bayesian chronological modeling (Bayliss Reference Bayliss2015), a practice that has been in place in the United Kingdom (especially in England through the work of Alex Bayliss and others at English Heritage/Historic England) for over 20 years. The body of well-sampled and well-dated sites subjected to Bayesian modeling in the United Kingdom is quite large, allowing for the first time generational narratives for many periods of British prehistory (Bayliss Reference Bayliss2015; Hamilton et al. Reference Hamilton, Haselgrove and Gosden2015). Much of this work has been undertaken in collaboration with a small group of archaeological specialists experienced in constructing robust chronologies (Bayliss Reference Bayliss2015). In many cases, they have produced chronologies of a higher accuracy, transparency, and reproducibility than those created through informal interpretation. The adaptation of Bayesian frameworks has also allowed for the estimation of detailed settlement histories and precise evaluations of the timing and tempo of social change.
The adoption of Bayesian chronological modeling outside Britain has occurred more slowly, but the method is now used regularly in many areas throughout Europe, Asia, and other parts of the world (Bayliss Reference Bayliss2015; Buck and Meson Reference Buck and Meson2015). The impact this work is beginning to have on European prehistory has been profound and has been referred to by some as a radiocarbon revolution (Bayliss Reference Bayliss2009). The majority of these applications are for site chronologies (Bayliss Reference Bayliss2015), but the method is also used to create environmental (Blaauw and Christen Reference Blaauw and Andres Christen2011; Bronk Ramsey Reference Bronk Ramsey2008; Dye Reference Dye2011), historical (Levy et al. Reference Levy, Higham, Ramsey, Smith, Ben-Yosef, Robinson, Münger, Knabb, Schulze, Najjar and Tauxe2010; Tipping et al. Reference Tipping, Cook, Mauquoy, Beresford, Hamilton, Harrison, Jordan, Ledger, Morrison, Danny Paterson, Russell and Smith2014), seriation (Denaire et al. Reference Denaire, Lefranc, Wahl, Bronk Ramsey, Dunbar, Goslar, Bayliss, Beavan, Bickle and Whittle2017; Whittle et al. Reference Whittle, Bayliss, Barclay, Gaydasrka, Bánffy, Borić, Draşovean, Jakucs, Marić, Orton, Pantović, Schier, Tasić and Vander Linden2016), and typological sequences (Conneller et al. Reference Conneller, Bayliss, Milner and Taylor2016; Garrow et al. Reference Garrow, Gosden, Hill and Bronk Ramsey2009; Krus Reference Krus2016).
The shift to chronological interpretation via Bayesian modeling has happened in large part because of the development of freely available computer programs, which provide user-friendly statistical modeling tools (Buck and Meson Reference Buck and Meson2015). The most widely used Bayesian chronological modeling software programs are BCal (Buck et al. Reference Buck, Andres Christen and James1999) and OxCal (Bronk Ramsey Reference Bronk Ramsey1998, Reference Bronk Ramsey2001, Reference Bronk Ramsey2008, Reference Bronk Ramsey2009a), and while the majority of applications are done in OxCal (Bayliss Reference Bayliss2015), other computer programs do appear (Jones and Nicholls Reference Jones and Nicholls2002; Lanos et al. Reference Lanos, Philippe, Lanos and Dufresne2016). Additionally, more specialized Bayesian chronological modeling software exists, primarily for age-depth modeling of paleoenvironmental sequences (Blaauw and Christen Reference Blaauw and Andres Christen2011; Haslett and Parnell Reference Haslett and Parnell2008). Nevertheless, the popularity of OxCal is due in large part to its capability for use in a wide range of applications.
The rapid growth in the implementation of Bayesian models within archaeology outside of the United Kingdom, combined with the dearth of practical learning materials, has led to confusion about the Bayesian process, the propagation of common myths, and in some cases outright skepticism. This story is familiar from a European perspective, even more so when examined from the perspective of bringing Bayesian modeling from England into standard archaeological practice in Scotland (which we have witnessed firsthand).
We believe it is both necessary and timely to provide a commentary on the state of Bayesian modeling in American archaeology to steer the discipline toward best practice approaches, especially since we have encountered skepticism and misconceptions in conversations with colleagues and in anonymous reviews, and because some of this is expressed in published literature. Many of these beliefs concern what is required to create proper and meaningful Bayesian chronological models, while others concern how to evaluate those models. Here we take to task six of these misconceptions.
We further provide a brief overview of the history of the use of the methodology in American archaeology. We describe in detail the Bayesian process, which is critical for understanding this methodology. We provide examples of the use of Bayesian chronological modeling in practice and a commentary on how Bayesian chronological modeling could be used in the future of American archaeology. Our goal in doing this is to bring a greater awareness of the key issues so that the practice can reach levels of quality comparable to that found in the United Kingdom and Europe.
The State of Affairs in the Americas
The first published studies using Bayesian chronological modeling in the Americas appeared in the 1990s, only several years after the first published applications in Europe (Bayliss Reference Bayliss2015). The exposition of the Bayesian method by Christen (Reference Christen1994) might contain the earliest published Bayesian chronological model for a site in the Americas—the Chancay culture of Peru—but it is the chronological modeling of Zeidler and colleagues (Reference Zeidler, Buck and Litton1998), with its discussion of contextual and taphonomic security and sensitivity analyses, that is more akin to the practice of chronological modeling that we outline in this article. While American applications of Bayesian chronological modeling continued to appear intermittently throughout the 2000s, only a handful of archaeologists used the procedures during that decade. From 2010–2015, there was an increase in the number of studies in American archaeology presenting applications, demonstrating that Bayesian chronological modeling in the Americas is on the verge of reaching critical mass (Figure 1, Supplemental Text 1).
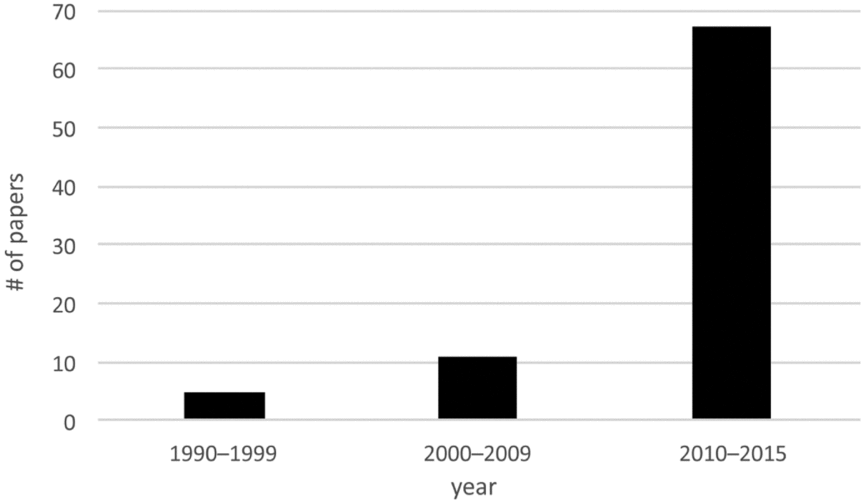
Figure 1. Histogram for the number of published Bayesian chronological modeling applications in American archaeology from AD 1990–1999, 2000–2009, and 2010–2015. See Supplemental Text 1 for a list of these references.
The rapid growth of Bayesian chronological modeling in American archaeology over the past several years and lack of formal training opportunities has led to plug-and-play applications, seemingly used by archaeologists without clear understanding of the Bayesian process (see Buck and Meson Reference Buck and Meson2015; Cowgill Reference Cowgill2015a:10). Likewise, there are problems with quality control of published studies due to a scarcity of qualified reviewers.
While there might not be a vocal demand for formal training opportunities, the need is clearly there. Whether they use Bayesian modeling or not, it is possible that over the next decade almost all archaeologists will see regional and site chronologies transformed from Bayesian modeling, and it is probably better that they be critically informed sooner rather than later. Some formal training opportunities we are familiar with in the Americas include a free online booklet about the basics of using OxCal (McNutt Reference McNutt2013), training courses that we have offered at various conferences, and a 2015 training course at the University of Arizona. Other resources often used for training are the OxCal Google Group (Google Groups 2017) and the OxCal online manual (Bronk Ramsey Reference Bronk Ramsey2017).
These training opportunities provide good introductions, but in many ways they barely scratch the surface. Becoming proficient in Bayesian chronological modeling takes a combination of training and experience, requiring a critical understanding of archaeology, methods used in scientific dating, and statistics. For many American archaeologists, training in how to use OxCal has come from self-learning, studying published literature, and discussing modeling with experienced American archaeologists. This has resulted in myths and misconceptions in the American literature about Bayesian chronological modeling.
Myths and Misconceptions
Misconception 1: Bayesian Statistics Is Overly Complicated Hocus-Pocus That Is Not Scientifically Objective
This belief is articulated by Stephen Lekson (Reference Lekson2015:166, 190–191) in several tongue-in-cheek comments in the second edition of The Chaco Meridian. For example:
Of course, there's a reason statisticians banned Bayes for a couple of centuries—and why Bayes’ heresies have been revived almost exclusively by the looser, weaker sciences (i.e., the social sciences). Bayes cheats: picking and choosing dates, modes, and so forth that fit one's preconceptions (or the statistical preconceptions built into OxCal) [Lekson Reference Lekson2015:191].
Contrary to Lekson's (Reference Lekson2015) claim, Bayesian statistics are widely used in the physical/natural sciences (see Supplemental Text 2 for an extensive but nonexhaustive list of relevant references). There is a degree of subjectivity in the Bayesian process. This is contained within our prior beliefs that combine to form the structure of the model. These beliefs are our interpretation of the archaeology and the inferences we make to relate the date of the death of a sample to the date of the formation of the deposit from which it was recovered. A “good Bayesian” does not pick and choose dates to fit one's preconception but rather rigorously defends their interpretation of the archaeology in a transparent manner to provide weight to the resulting date estimates. The central issue in this myth is the scientific objectivity of the process, which allows us to delve into the underlying mathematics, in brief.
While OxCal is a program with complex underlying algorithms, the fundamental mathematics of all Bayesian applications follow Bayes's rule (following Bayliss Reference Bayliss2009; Buck et al. Reference Buck, Kenworthy, Litton and Smith1991, Reference Buck, Cavanagh and Litton1996). Bayes's rule (also called Bayes's law or Bayes's theorem; Equation 1) was proposed by the English mathematician and Presbyterian minister Thomas Bayes in the 1700s (Bayes Reference Bayes1763; Kruschke Reference Kruschke2014):
 $$\begin{eqnarray}
\textit{posterior} &=& \frac{{{\rm{likelihood}} \times {\rm{prior}}}}{{{\rm{evidence}}}} = p\left( {\theta \left| D \right.} \right)\nonumber\\
& =& \frac{{p\left( {D\left| \theta \right.} \right) \times p\left( \theta \right)}}{{p\left( D \right)}}
\end{eqnarray}$$
$$\begin{eqnarray}
\textit{posterior} &=& \frac{{{\rm{likelihood}} \times {\rm{prior}}}}{{{\rm{evidence}}}} = p\left( {\theta \left| D \right.} \right)\nonumber\\
& =& \frac{{p\left( {D\left| \theta \right.} \right) \times p\left( \theta \right)}}{{p\left( D \right)}}
\end{eqnarray}$$
Where: ![]() $p( D ) = \mathop \sum_\theta p( {D| \theta } )$
$p( D ) = \mathop \sum_\theta p( {D| \theta } )$
The equation provides a model for estimating the probability of a belief after the collection of data that can test the belief. The key factors of a model that follows Bayes's rule are the belief (θ) being tested, the prior, the likelihood, the evidence (D), and the posterior. In Equation 1, p(θ) and p(D) are probabilities for observing these two events independently of one another, whereas p(D|θ) and p(θ|D) are conditional probabilities of observing the first event given the second event is true.
It is too early in the article to lose readers, so a simplified depiction of Bayes's rule is shown in Equation 2, where the relationship of the likelihood and evidence is simply referred to as the “standardized likelihood” (Buck et al. Reference Buck, Kenworthy, Litton and Smith1991:811).
This is further refined into terms recognizable to archaeologists with the “standardized likelihood” equivalent to our “dates” and our “prior,” which equates to date probabilities in a chronological model (Equation 3).
 $$\begin{eqnarray}
&&{\rm{Posterior}}\,{\rm{Beliefs}}\nonumber\\
&&\quad = \,{\rm{The}}\,{\rm{Dates}}\,\left( {{\rm{Standardized}}\,{\rm{Likelihood}}} \right)\nonumber\\
&&\quad {\rm{ \times }}\,{\rm{Archaeological}}\,{\rm{Data}}\,\left( {{\rm{Prior}}\,{\rm{Beliefs}}} \right)\nonumber\\
\end{eqnarray}$$
$$\begin{eqnarray}
&&{\rm{Posterior}}\,{\rm{Beliefs}}\nonumber\\
&&\quad = \,{\rm{The}}\,{\rm{Dates}}\,\left( {{\rm{Standardized}}\,{\rm{Likelihood}}} \right)\nonumber\\
&&\quad {\rm{ \times }}\,{\rm{Archaeological}}\,{\rm{Data}}\,\left( {{\rm{Prior}}\,{\rm{Beliefs}}} \right)\nonumber\\
\end{eqnarray}$$
Lindley (Reference Lindley1985) provides a good overview of Bayesian inference for the non-statistician, while Kruschke (Reference Kruschke2014) is accessible to the mathematically minded reader. The Bayesian process is very much like the way that we intuitively learn as humans and change our beliefs to improve our individual understandings. We start with our prior beliefs about how and why things and events happen. Then through our life experience, we modify our beliefs to suit what we have experienced. If our experience confirms our beliefs, then they are supported. If our experience is contrary to our beliefs, then our beliefs may change.
Radiocarbon and other scientific chronological information are used in Bayesian chronological modeling to calculate the standardized likelihood and are modeled in different ways to reflect the prior strength of our beliefs about the functional relationship of the data (Bayliss Reference Bayliss2009). The posterior probabilities estimated by OxCal serve as posterior probabilities for functions specified in the model such as individual radiocarbon calibrations and model boundaries. To do this, OxCal (version four and above) uses a Markov chain Monte Carlo (MCMC) and Metropolis-Hastings algorithm to generate random draws from a target distribution and produce a range of posterior probabilities (Bronk Ramsey Reference Bronk Ramsey2009a; Gelfand and Smith Reference Gelfand and Smith1990; Gilks et al. Reference Gilks, Richardson and Spiegelhalter1996). Bronk Ramsey (Reference Bronk Ramsey1998, Reference Bronk Ramsey2001, Reference Bronk Ramsey2009a) describes the finer details about the algorithms used for this process.
It is critical that users of Bayesian modeling software understand the Bayesian modeling process, the mathematics of the software packages used, and how to avoid “black boxing” the presentation and interpretation of their models. If careless modeling is published due to lack of a critical evaluation, then the results should be treated skeptically. Analytical transparency is key for evaluation but also for expanding upon the modeling in the future. Bayliss (Reference Bayliss2015) and Buck and Meson (Reference Buck and Meson2015) describe in detail what “good” Bayesian modeling studies should include.
Misconception 2: Old Radiocarbon Measurements with Large Errors Should Be Ignored
Occasionally, we come across the belief that legacy radiocarbon dates with large standard errors are of little interpretative value because of their greater imprecision. For example, Connolly (Reference Connolly2000) rejects radiocarbon measurements with errors > 100 years in an analysis of dates from Poverty Point. Additionally, it may be questionable if a legacy radiocarbon date is even an accurate measurement. For example, calibrations of dates from Alaska made by the Dicarb laboratory have been noted in some cases to be too young (Reuther et al. Reference Reuther, Wu, Craig Gerlach, Wang and Zhou2005).
It is easy to understand why someone might want to exclude these measurements. If the aim of the Bayesian model is to improve chronological precision, then the removal of measurements with large errors gives the immediate appearance of increased precision. This is because the “traditional” methods of evaluating radiocarbon dates (e.g., summed probabilities or “eyeballing” calibrations) will be significantly affected by the addition of these results; however, not only can a Bayesian model handle these data effectively but these dates may actually have the most secure connection between sample and event (e.g., charcoal in a hearth or animal burial). Despite their issues, legacy dates with large standard errors can be informative data for a Bayesian model (see Bayliss et al. Reference Bayliss, van der Plicht, Bronk Ramsey, McCormac, Healy, Whittle, Whittle, Healy and Bayliss2011; Jay et al. Reference Jay, Haselgrove, Hamilton, Hill and Dent2012; Krus et al. Reference Krus, Cook and Hamilton2015). We admit that modeling these older radiocarbon dates can be difficult; it is sometimes unclear exactly what was dated and what dating methods were followed (a problem sometimes associated with legacy dates of smaller errors as well). Finding this information can involve much research, including contacting the original submitters and laboratories, but this is necessary to fully evaluate the accuracy of the data and to decide how to include them in a Bayesian model. In cases where legacy dates are questionable, they could be cross-checked by redating the original samples or contemporaneous material.
Additionally, one should consider alternative models or sensitivity analyses, which are key elements in Bayesian chronological modeling (Bayliss et al. Reference Bayliss, van der Plicht, Bronk Ramsey, McCormac, Healy, Whittle, Whittle, Healy and Bayliss2011; also see Kruschke Reference Kruschke2014) but which are often missing in archaeological applications. With a sensitivity analysis, we amend the prior information to determine which of the model components are most critical in estimating the posteriors. Bayliss and colleagues (Reference Bayliss, van der Plicht, Bronk Ramsey, McCormac, Healy, Whittle, Whittle, Healy and Bayliss2011) praise the strength of this technique and emphasize that it is useful for demonstrating the robusticity of a preferred model.
Misconception 3: Stratigraphic Relationships between Samples Are Needed to Make a Bayesian Chronological Model
Following this belief, Bayesian chronological modeling is not possible in circumstances where there is little-to-no stratigraphy between radiocarbon samples. On the contrary, there are numerous models from radiocarbon data that are not constrained by stratigraphic relationships (e.g., Bayliss et al. Reference Bayliss, Bronk Ramsey, van der Plicht and Whittle2007; Hamilton and Kenney Reference Hamilton and Kenney2015). This is possible because these models use a uniform prior distribution (UPD) that assumes that any event in the model is equally likely to have occurred in any individual year covered by the data (Bronk Ramsey Reference Bronk Ramsey1998:470). Whereas stratigraphic relationships are an informative type of prior information, uniform prior distributions are an uninformative belief that structure data as a continuous period of activity (Bayliss and Bronk Ramsey Reference Bayliss, Bronk Ramsey, Buck and Millard2004:33; Bronk Ramsey Reference Bronk Ramsey2009a:354). It is only justifiable to use a UPD if the dated activity is believed to be continuous, whether it be for a short or long time or at a slow or fast tempo.
A couple of recent American studies have approached modeling without stratigraphy by placing dates in a sequence from oldest to youngest (e.g., R. Cook et al. Reference Cook, Ascough, Bonsall, Derek Hamilton, Russell, Sayle, Marian Scott and Bownes2015; Lekson Reference Lekson2015:190). Unfortunately, this informative prior information is unsubstantiated. One should not use priors that do not reflect the archaeology. Even if they help provide more precise posterior probabilities, the underpinning assumptions are unfounded (Buck and Meson Reference Buck and Meson2015:571).
Misconception 4: The Date for a Diagnostic Prehistoric Artifact or Expected Time Range of Activity Should Be Included in the Model to Provide a Chronological Constraint
Calendar dates can be used in a Bayesian model to constrain the model results by specific years. For example, a site containing an abundance of artifacts of a presumed date could be modeled to constrain independent dates from the site to this specific period. However, results will then conform to this expectation, such that you build a model to ensure you never learn something new!
Including calendar years within a model can only be justified if they reflect the known time of a historic or geological event strongly related to the archaeology. Otherwise, this practice becomes fuzzy, especially where the evidence is diagnostic artifacts not obviously linked to specific calendar years (e.g., pottery versus coins). If applied loosely, this practice results in a tautological loop, where the scientific dates should produce independent estimates but are modeled to fit the preconceived beliefs about the timing of the associated artifacts. Further, there are taphonomic considerations and the final (re-)deposition of diagnostic artifacts may be greatly removed from the timing of their creation, such that their incorporation into a model often only provides a terminus post quem (TPQ; limit after which) for the formation of the deposit from which they were recovered. If calendar years are used to constrain the model, then a sensitivity analysis should be used to show how the results change when calendar year constraints are removed.
Misconception 5: The Agreement Indices in OxCal Are a Useful Tool for Determining Which Competing Model Is More Probable
We occasionally see papers and presentations where agreement indices are misinterpreted as values indicating a most probable model (e.g., Riede and Edinborough Reference Riede and Edinborough2012). OxCal's agreement indices are like Bayes factors, which is a type of calculation used to compare the probability of Bayesian models (Gilks et al. Reference Gilks, Richardson and Spiegelhalter1996; Kruschke Reference Kruschke2014). Importantly, OxCal's agreement indices are not actual Bayes factors, but rather pseudo Bayes factors, and should only be used to determine if a model is consistent or inconsistent (Bronk Ramsey Reference Bronk Ramsey1995:427–428, Reference Bronk Ramsey2001:355). The indices are numerical values for the agreement between the OxCal model and data. Values less than 60 indicate the chronological data and model are inconsistent, while those greater than 60 indicate consistency (Bronk Ramsey Reference Bronk Ramsey1995:427–428), with the value of 60 similar to the 95% probability in a chi-square test. Amodel provides a value for the agreement of the entire model, and Aoverall is a function of agreement indices of the individual dates.
Misconception 6: Bayesian Modeling Is Not Necessary if You Have a Widely Accepted Site/Regional Chronology
The final misconception is that Bayesian modeling is not necessary for a site or region where a chronology is already established through diagnostic artifacts or perhaps other forms of scientific or historic dating. The reality is that it is impossible to know the results from Bayesian modeling if not attempted. If the modeling produces the same interpretation as preexisting chronological beliefs, then that is a noteworthy finding as it makes those beliefs stronger. If the modeling has a different interpretation, that too is important. If it is between reaffirming older interpretations and forging new ones, then the application of Bayesian modeling should result in a discussion worth having.
The Bayesian Process
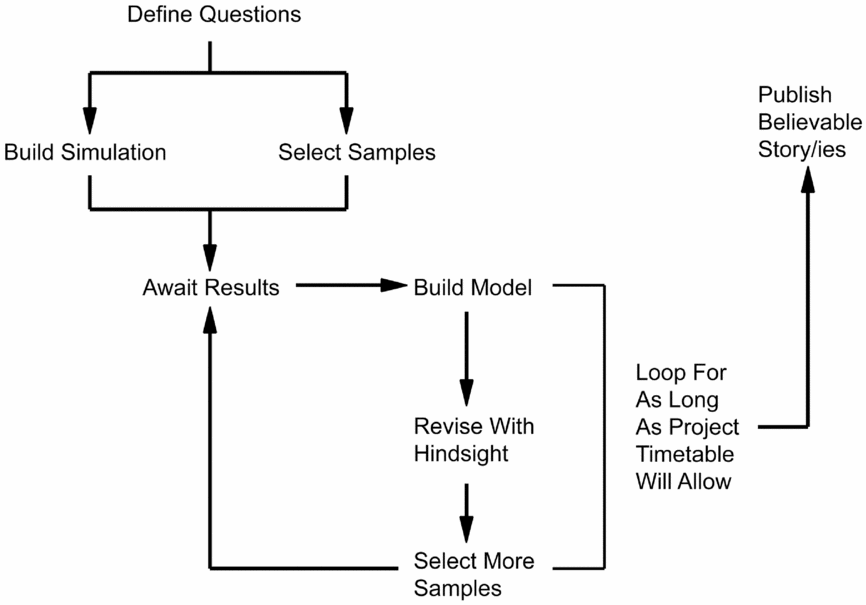
In the previous section, we tied the major misconceptions regarding Bayesian modeling directly to a lack of fundamental understanding regarding how the process works both in theory and in practice. Here we wish to lay bare the process to make clear that there is both objectivity and scientific rigor inherent in the choices made throughout the chain. The modeling approach can be distilled into the schematic shown in Figure 2, which is derived from and described in more practical detail by Bayliss and Bronk Ramsey (Reference Bayliss, Bronk Ramsey, Buck and Millard2004).
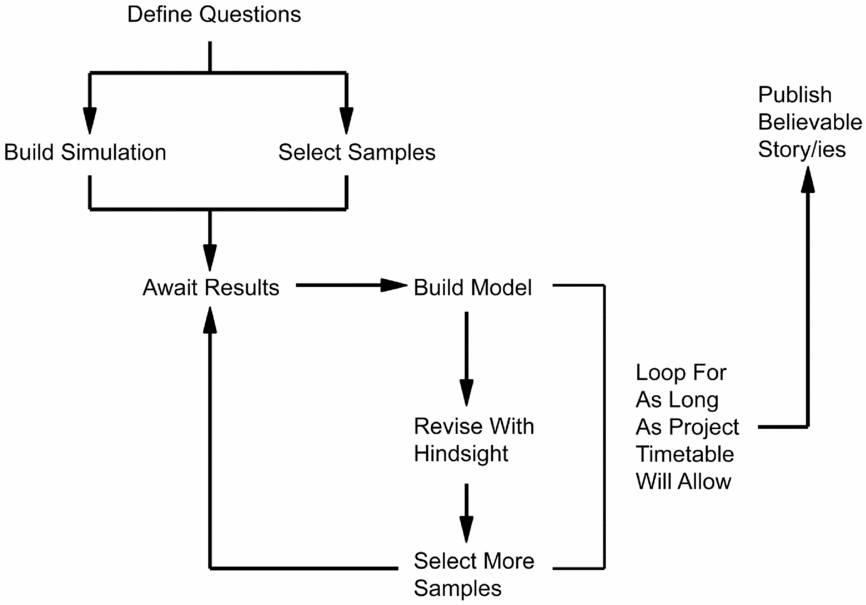
Figure 2. The Bayesian method in practice (after Bayliss Reference Bayliss2009:Figure 9; Bayliss and Bronk Ramsey Reference Bayliss, Bronk Ramsey, Buck and Millard2004:Figure 2.2).
Assess Existing Data and Knowledge
“Existing data and knowledge’” refers primarily to legacy dating, but other forms of chronological information should be noted (e.g., probable date based on artifacts), as these can also be useful to help inform some of the decisions made further along. Any legacy radiocarbon dates—old dates that a project has inherited from other archaeologists—will need to be thoroughly critiqued. Many archaeologists who have developed, or acquired, large radiocarbon databases have recently been undertaking some form of “data cleansing” prior to analysis and interpretation, but this can be an exercise (i.e., if error > 100, then reject radiocarbon age) that misses the importance of holistically understanding the sample, context, and date. At the very least, it is necessary to have a description of the dated sample, the specific laboratory methods, and the sample's provenience in relation to the archaeological features. As mentioned above, this process can be very laborious. Recently, we were faced with a series of radiocarbon dates from the SunWatch site near Dayton, Ohio, that were not chosen by us but that we wanted to model (Krus et al. Reference Krus, Cook and Hamilton2015). One of the dates (M-1965) had contradictory information. While the Michigan date list indicated the sample was made up of “small pieces of charcoal from 6 or 8 of 20 refuse pits excavated” (Crane and Griffin Reference Crane and Griffin1970:166), a reevaluation of the site archive by Cook (Krus et al. Reference Krus, Cook and Hamilton2015) made it clear that this sample is most likely from a single refuse pit, Feature 6/8. The unidentified nature of the charcoal was still problematic, since there could conceivably be fragments that would otherwise incorporate an old wood offset, but at least we were confident that the material came from a single feature and was not a composite from many different features!
In critiquing legacy dates, the aim is to produce a commentary of reasons why each date accurately reflects the date of the deposit within which its sample was found, and furthermore, to provide clear explanations for the scientific and/or taphonomic issues associated with any dates that are deemed to provide unreliable dating evidence for the formation of its context. The connection between a sample, its context, and the event under consideration is the most critical and tenuous link in the Bayesian modeling process (Dean Reference Dean and Schiffer1978). Not only does it apply to how we critique our legacy dates but it also informs which samples are suitable for dating and, ultimately, the types of chronological questions we can approach.
Define Problems
The most basic and common problem or question pertaining to site-based models concerns the timing and span of activity; for many sites, in many periods, these can be answered satisfactorily with as few as a dozen well-chosen dates and no stratigraphy. As the archaeology and models become more complex, more nuanced chronological questions might arise, such as the date when a specific transformation of the site (e.g., building of a palisade or digging of a ditch) or internal event (e.g., construction of a house) occurred. Where there are multiple rebuilt houses or re-dug ditches, we might be able to delve into the realm of the tempo of change and search for temporal regularities to activity that might be interpretable within the scale of a single human lifetime.
Site-based questions can be scaled up to consider the timing of events and temporality of processes at regional, or even continental, scales. Regional chronologies are constructed in many ways, but the Bayesian approach almost invariably starts with an evaluation of the dates on a site-by-site and context-by-context basis. The types of models that are not wedded to site-based models are usually concerned with the currency of an artifact type, whereby dating an artifact directly (e.g., bone comb) or organic material in direct association with the artifact (e.g., organic residue on a pot) provides the required connection between sample, date, and question.
Identify Samples
Armed with the questions you want to answer, it is time to identify the contexts that contain samples suitable for dating, thereby giving you the best chance at success. Bear in mind that just because problems have been defined, samples suitable to achieve a satisfactory solution may not be available, so that the availability of suitable samples can dictate the range of possible questions.
This is usually the point where we would consider a sort of hierarchy of sample types, but to rank the samples on a ladder is potentially misleading, as a high-ranking sample might have low utility for some questions (cf. Bayliss Reference Bayliss2015). The general point about ranking your samples is to have samples that you can demonstrate, or argue, provide an accurate date for the deposit from which they were recovered. This does not mean that simply because a deer femur was recovered from a ditch fill, it dates when the ditch was open or infilling. In many instances, a disarticulated animal bone provides a low level of confidence, especially the smaller ones that easily can be bioturbated or anthropogenically redeposited. However, if part of a deer was recovered in articulation (e.g., foot bones) from this ditch, then we could argue that it went into the ground soon after the death of the animal and should accurately date when that deposit formed. Our disarticulated femur provides, at best, a TPQ for the infilling of the ditch.
In addition to articulated remains, samples functionally related to their deposit are usually a sound choice. Here we might select charcoal or charred grain from a hearth or oven, where we can confidently infer that the material in the feature had recently died and burned in situ. We might also extend this to a discrete dump of burned material in a pit or ditch interpreted as possible hearth waste. While there is likely an unknown lag between when the wood was collected and used and when the hearth was cleaned out, this offset is almost certainly negligible, and in this example likely not to be even a year.
Build Simulation Models, Submit Samples, and Assess Results
With a solid understanding of the questions to be tackled and a list of the suitable samples available, it is time to construct simulation models and assess the possible results given these inputs and our current archaeological knowledge (see Bayliss et al. Reference Bayliss, Bronk Ramsey, van der Plicht and Whittle2007; Steier and Rom Reference Steier and Rom2000). This stage of the process is very much about trying to understand how the number of dates available (constrained either by physical suitable samples or finances), the relevant area of the calibration curve, and such information as the relationship between samples or shape of the prior probabilities applied to the dates all combine to produce an answer. This stage of “getting a feel for the data” is critical in the Bayesian process; it is the point where the modeler becomes so familiar with how the priors and data work together that they can intuit how a change to one part of the model might affect the outcomes (Buck and Meson Reference Buck and Meson2015).
Guided by the simulation results, samples are submitted. The role of the simulation is to optimize the sample selection process, but only a portion should be submitted in the initial round. Most dating programs following a Bayesian approach will have several rounds of dating. After receiving the results, we go back to our pool of potential samples and begin to simulate the results for adding radiocarbon results from another round of dating and loop the process. By going through a series of simulations before submitting each round of samples, we can see what effect results from additional samples in specific areas of the model will have, thereby enabling us to problem solve at each stage and manage expectations.
Finalizing Models
Developed simulations should lead to the construction of the primary model. If there are multiple readings of the archaeology or other prior information that can be added to the analysis, then additional models will be constructed for a sensitivity analysis. Further, as part of the modeling process, it is always important to undertake quality assurance in the form of replication of some of the dates. Replication might include submission of two samples of the same type (e.g., charcoal of different species) or different types (e.g., grain and animal bone) from the same context as a means of checking the security of the deposit or to look for offsets. In some cases, it may be desirable to split a sample and send it to two different laboratories as a means of independently verifying the results. While there is no hard rule on the level of replication one should undertake, we would suggest replicating somewhere on the order of 10% of the dates, with more replication occurring where there is greater uncertainty in the taphonomic security or general overall quality of the samples.
Publish Results and Interpretations
After all the work in dating samples and developing models, the results and interpretations are written up for publication. It is at this stage all the assumptions and choices that went into constructing the models should be put forth in an accessible manner, allowing the reader to properly critique the work. Oftentimes, the necessary level of transparency is lacking. While this article is neither a how-to manual for Bayesian modeling nor a set of best practice guidelines, the following are a few tips that will be helpful for a reviewer/reader:
1. Clearly define the model structure in the publication and link the “death” of the dated sample to the formation of the deposit or archaeological event of interest. If a radiocarbon date does not fit expectations, explain why and determine the reason for the misfit (e.g., contamination, insecure context, lab error, or statistical outlier).
2. Include the full model figure that shows the structure that has been described (e.g., the OxCal brackets and keywords). This should allow other researchers to re-create the model precisely, for all but the most sophisticated solutions. Consider including the raw code used to create the model as supplemental data. Similarly, consider including any prior probabilities that are not clearly defined.
3. Where durations are given in the text (e.g., span of an occupation, time between two events), include a figure of that probability. This is especially useful to demonstrate that a span might be skewed to a younger or older range.
In addition, there are a few conventions for reporting the modeled probabilities that may reduce readers’ confusion:
1. Round modeled probabilities outward to five years. This is not a “rule” by any means, but the IntCal13 calibration curve is constructed using a five-year random walk algorithm, and much of the data underpinning the curve are from decadal tree-ring samples. In addition, the rounding often accounts for slight differences in results from the different runs of a model and is easier for most people to retain in their heads.
2. Make certain to refer to any modeled or calibrated dates as “cal BC/BCE” or “cal AD/CE” (or “cal BP”).
3. Italicize modeled dates to set them apart from simple calibrated dates and inform the reader that you have done so because they are the result of an interpretative model.
A final note: uncalibrated radiocarbon ages are given as means and standard errors, thus approximating a normal distribution, making reference to 1- and 2σ ranges perfectly acceptable. However, calibrated radiocarbon dates and modeled probabilities are in no way normally distributed, and so their ranges should be referred to by the percent of the area of the probability represented below the curve (i.e., 68.2% or 95.4%). Oftentimes, when rounding the date ranges, the precision of the percent beneath the curve can be found to be truncated simply to 68% or 95%.
The Bayesian Practice
While a discussion of the Bayesian process, as abstracted above, will sit well with many readers, we present here briefly an example of the process in practice. We consider a site consisting of negative (i.e., cut) features, with a rectangular post-built structure with central hearth, a few pits, and an enclosure ditch. The aim with this hypothetical example is to elucidate the thought process of the Bayesian modeler, while highlighting those areas of the modeling process that can be especially challenging. In this example, we use the terminology implemented in the OxCal program, but the ideas remain the same whether using OxCal, BCal, or other programs. For ease, we use boldface font to denote the specific OxCal commands.
Defining the Problem
The first thing is to define the archaeological questions. In this case, we might want to know (1) when did activity begin, (2) when did activity end, and (3) for how long did this activity take place? These are the most basic questions asked of any site-based model because they refer to the broadest level of chronological inquiry. We cannot stress enough that these questions are almost never answerable by a single radiocarbon date but are estimates derived from a chronological model that is composed of dates related to the activity that occurred between the actual start and end date at the site. While there may be instances that the modeled probability for a specific radiocarbon date is important or interesting (e.g., a burial, material associated with a specific artifact), more often than not it is the “events” that occur before, after, and between the archaeological residues, which form the sampled material, that have particular meaning.
The two main building blocks of models are the ordered (Sequence) and unordered (Phase) groups. Thinking of the site described above, we might feel safe in assuming it is all a single period of occupation (there may even be artifactual evidence from across the site to suggest that it is all broadly contemporary). We have no defined relative ordering (e.g., stratigraphy) between any of the features, and so we can begin thinking about our radiocarbon dates “existing” as an unordered group—a Phase. Given our assumption that the features are all related to a single period of activity, we can progress and add two elements in the form of a “start” and “end” Boundary, and situate these three elements within a Sequence. By doing this, we have explicitly instructed the computer program that at some point in time in the past, for which we do not have a date, activity began on the site. The activity went on for some unknown duration, and then it ended. Furthermore, we have also defined that activity began before it ended.
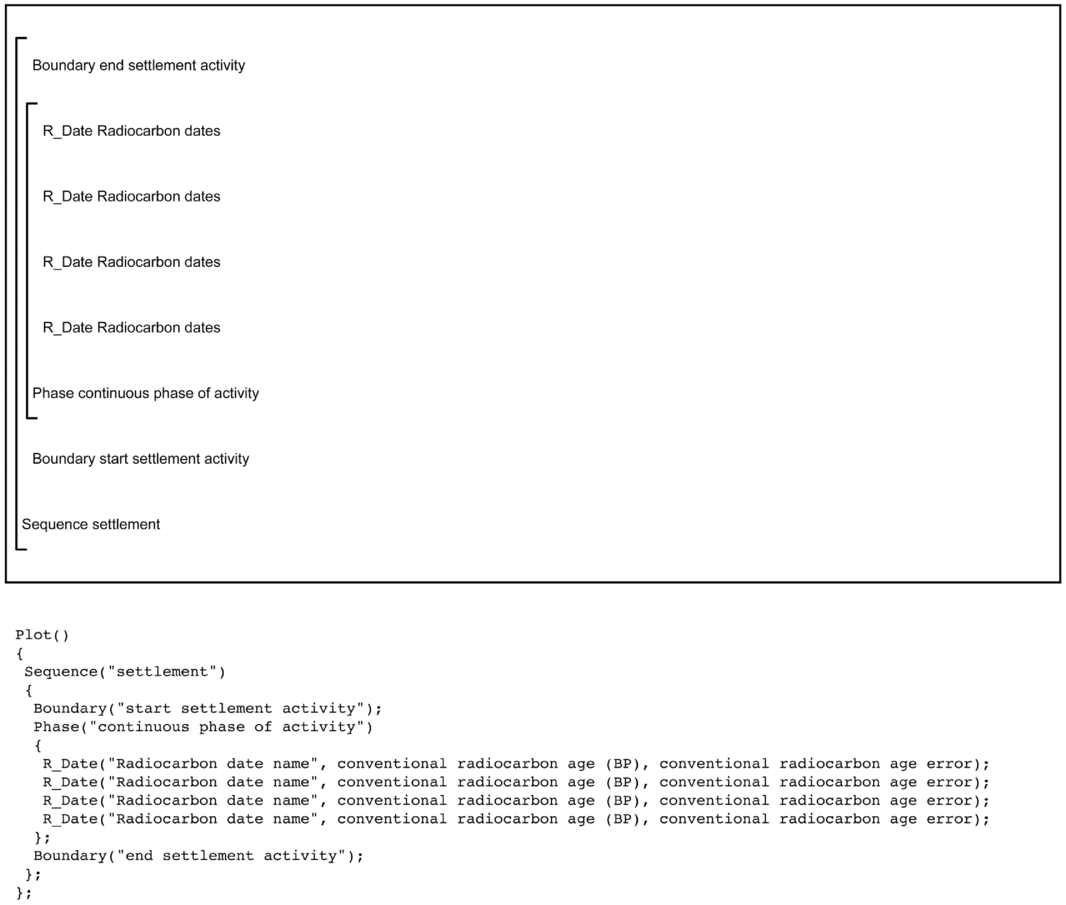
At the most basic level, a Boundary defines the time that the dated activity begins and ends (Bronk Ramsey Reference Bronk Ramsey2001; Steier and Rom Reference Steier and Rom2000). They are placed within a Sequence as this sets up the necessary ordered relationship that activity begins, material that can be dated is deposited, and activity ends. Often boundaries are used to represent that start or end of activity at a settlement or of a phase of discrete activity within a settlement. Crucially, the time of a Boundary is estimated in a Bayesian chronological model, which provides archaeologists probabilistic estimates for events (such as the start of activity at a settlement) that cannot be directly dated. Figure 3 visually demonstrates how Boundary, Phase, and Sequence are incorporated into a simple Bayesian chronological model for an archaeological settlement with no dates from intercutting features. Algebraically, this model can be expressed as αsettlement > Θsettlement > βsettlement, where Θsettlement is the set of dated events θ 1 . . . θ n from the continuous phase of settlement activity, represented by the radiocarbon-dated samples.
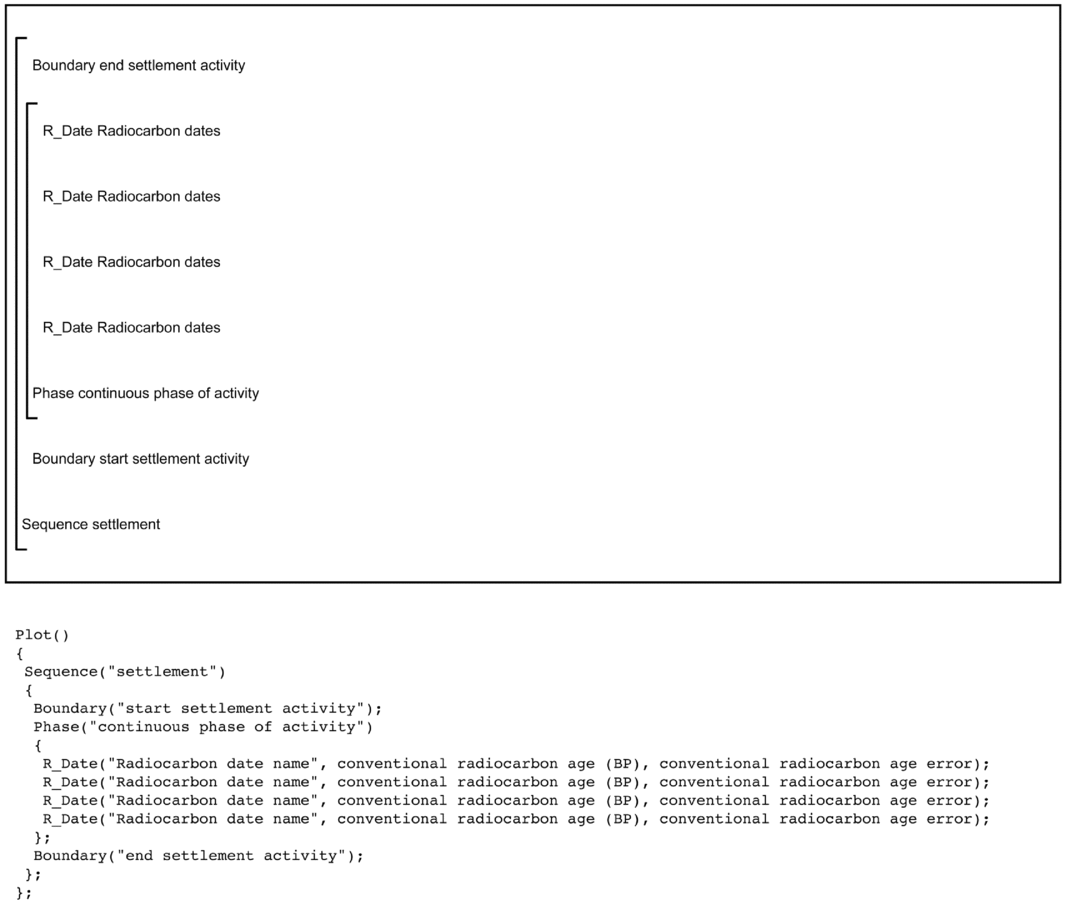
Figure 3. Bayesian chronological model structure demonstrating the use of radiocarbon measurements within Boundaries, Sequence, and a Phase. The large square “brackets” along with the OxCal keywords define the overall model exactly. The OxCal script for the model is shown below the model structure.
When using the standard Boundary parameters in OxCal, the program will apply a uniform prior distribution (UPD) to the radiocarbon dates contained within the Phase. The UPD essentially indicates that activity goes from nil to maximum intensity, stays at maximum intensity for some time, and then switches back to nil. This is the simplest form of chronological model, with the UPD being an uninformative prior, helping to constrain the dates based on the statistical scatter within the group. There are different “boundaries” that can be used, enabling the start and end to be modeled as a steady or steep ramp, thereby altering the prior distribution being applied to the dates (Lee and Bronk Ramsey Reference Lee and Bronk Ramsey2012). Despite the ability to alter the prior that is applied to the group of dates, the UPD is extremely flexible and robust (Bayliss and Bronk Ramsey Reference Bayliss, Bronk Ramsey, Buck and Millard2004), and we suggest that in most cases, if alternative priors are used, that the UPD be run as a sensitivity analysis so that it is possible to see the effect that different boundaries have on the final results.
The simple model described above is often referred to as a “Phase model” or “Bounded Phase model” and takes its name from the OxCal command that is similarly named Phase. It is important to stress here that this is in no way similar to a traditional archaeological phase based on such things as ceramic or projectile point typologies. This type of model is extremely versatile and finds use in any situation where there is no relative ordering between samples (e.g., series of pits or the posts from a house).
The Sequence is especially powerful, with the temporal relationship it sets up between dates acting as an informative prior. Like the Phase, the Sequence can form the basis of the model structure, such as with a series of dates from an environmental core. But its versatility lies in the ability to function as a building block within a more complex model structure. Thinking of our hypothetical site, if we dated sequential charcoal lenses in the ditch, then we could place those dates into a Sequence within the overall unordered group of dates within the Phase. The informative prior only affects those stratigraphically related dates but allows them to contribute to the mathematics applied to the overall group.
Not only can Sequences exist within a Phase, but a Phase can exist within a Sequence. This nesting of ordered and unordered groups of dates allows the construction of complex models from complex archaeological sites. This level of model complexity is beyond the scope of this article, but we direct the reader to the work of Harris (Reference Harris1989) for a discussion of single-context recording and the production of Harris matrices, as well as Dye and Buck (Reference Dye and Buck2015) for discussion of the use of matrices and diagrams for developing models and displaying their structure.
Creating models using the building blocks (Phase and Sequence) is a straightforward exercise since often what is being modeled are the relationships observed or inferred between samples or dated contexts. However, the ease of this element of the process can have the deleterious effect of leading people to take a plug-and-play approach to chronological modeling instead of focusing on the most tenuous element of the entire chain: the relationship between the date of the sample and the date of the context.
Selecting the Samples
As the prior information becomes more informative (e.g., stratigraphic relationships are included), it becomes increasingly important to minimize the time lag between the date of the death of the sample and the date of the formation of the deposit. This is where the notion of the hierarchy of samples, alluded to above, becomes a useful device. While there is no strict best or worst sample, our goal in almost every case is to select a sample whose radiocarbon date is the same as the date it was buried in the context from which it was recovered. Taphonomic understanding is critical for understanding how the dates of the two events (sample death and context formation) are related, and for this reason, bone that is recorded as articulated during excavation, or noted as likely having been articulated when undergoing post-excavation analysis, is often considered to be the gold standard for site-based models. These samples are unlikely to have remained intact for any long duration before burial. Unfortunately, these samples are a rarity on most archaeological sites, and so many of the modeled samples will either have a functional or inferred relationship made between the sample and formation of its context.
Defining a functional relationship between a sample and context is not a difficult task, and one that archaeologists regularly do as part of the excavation process. Arguably, the most ubiquitous sample from a site is charcoal, and if that charcoal comes from a hearth, it is possible to define this functional relationship to explain both how and why that sample was recovered from that feature. Another sample that has a clear functional relationship is a charred food residue on a sherd of pottery, the date from which should reflect the date of the foodstuff that was burned (this is barring any potential reservoir offset in the date).
The next tier sample is where the relationship to the context can be inferred, and here we are referring to things such as discrete dumps of charred material that may be interpreted as the debris cleaned out from a hearth or charred debris from the use of a structure that has filtered down into the posthole that forms as an internal post decays. In all cases, it is important that the relationship be defined, and the more tenuous the link, the more rigorously the taphonomic relationship must be defended. Turning back to our hypothetical site, we would look first and foremost for samples such as articulated/ing animal bone in the pits or ditch or short-lived samples of charcoal or charred cereals in the hearths, and finally for similar charred debris in the postholes of the houses or as discrete fills in the ditch.
Dealing with Age Offsets, Outliers, and Misfits
Even after defining realistic problems and selecting and submitting secure samples for dating, it is likely that some of the dates will not conform to prior expectations. The results can be either older or younger than expected, and as a rule of thumb, all samples should be considered residual (i.e., redeposited) until otherwise demonstrated. Beyond reevaluating the probable taphonomic history of a sample, we should consider other potential sources for error, including the possibility for an in-built age offset or sample contamination.
In-built age offsets describe instances where the radiocarbon age is older than would be expected, given the date the organism died. Generally, when dealing with samples that have not been mishandled or undergone any form of conservation, there are two primary age offsets that we must consider: (1) old wood offset, and (2) reservoir offset, commonly in the form of a dietary offset.
Demonstrated old wood offsets in charcoal are often used as a reason to discount archaeologically unacceptable radiocarbon results. The reality is that all wood samples that are not bark or the final ring will have a radiocarbon age that is a weighted mean (by mass) of the radiocarbon content of all the rings in the sample. By selecting short-lived species, or twiggy pieces of wood from a sample, the offset is minimized, and when the models also include animal bone and seeds, the minor offset in the charcoal samples will be negligible to the model results. Where there is some confusion, or lack of documentation, about what charcoal was dated, rather than exclude a date from a model, it is completely acceptable to include the result as a TPQ for the formation of the deposit. Furthermore, formalized statistical tools are available in OxCal that allow for an old wood offset in charcoal to be modeled, in the form of a Charcoal Outlier Model (Bronk Ramsey Reference Bronk Ramsey2009b). This form of model can be especially useful when attempting to achieve very high precision and nearly all the samples are on charcoal (see Hamilton and Kenney [Reference Hamilton and Kenney2015] for a worked example), as the dates in the model most likely to be outliers have their effect on the results downweighted.
The second offset we consider is a result of the carbon in the sample not being in equilibrium with the terrestrial biosphere, a reservoir offset. This commonly occurs through a marine reservoir effect (MRE), with the global average marine offset equivalent to approximately 400 years, but can also take the form of a freshwater reservoir effect (FRE), usually the result of dissolved geologic carbon (e.g., radioactively “dead” in terms of 14C) in a freshwater lake or stream. When plants photosynthesize in these environments by taking in CO2 from the water, they incorporate this age offset, which propagates along the food chain. While MRE and FRE add a layer of complexity to analyzing and interpreting radiocarbon dates, it is possible to accurately model the dates of species from the marine environment (e.g., fish, seals, whales) and even model the dates from omnivores that received all or part of their dietary protein from marine species (G. Cook et al. Reference Cook, Comstock, Martin, Burks, Church and French2015). Correcting for FRE is slightly more difficult as it requires calculating the FRE for a specific place and time, with the correction made to the uncalibrated radiocarbon age. Using new Bayesian tools to “unmix” the contribution of terrestrial, marine, and freshwater protein to an individual's diet, it is possible to robustly model the dates of individuals who consumed animals with both an MRE and FRE (Sayle et al. Reference Sayle, Derek Hamilton, Gestsdóttir and Cook2016).
After considering these forms of offset and error, it is important to remember that even radiocarbon laboratories can make mistakes. While labs have stringent internal quality assurance protocols, there are instances where a date is simply incorrect with no indication of what went wrong. This is one reason why replication is important, and if possible, the replication should be made using a second laboratory as the additional check. Finally, it is important to remember that the radiocarbon dating process is a statistical one, where the result received from the laboratory is a probabilistic statement—a measurement mean and standard error—that at 2σ (95.4% probability) should contain the real radiocarbon age. Therefore, we should expect one in 20 radiocarbon ages to fall outside of the 95.4% probability range and can only hope that it is not so far outside that range as to make our interpretations importantly wrong.
Conclusion
Many American archaeologists are now aware of studies employing Bayesian chronological modeling and are either experimenting with applications for the first time or working with collaborators. Recently, in a Latin American Antiquity forum essay, Cowgill (Reference Cowgill2015b) strongly encouraged American archaeologists to adopt Bayesian chronological methods. In addition to the published literature, this interest is evident from the increasing number of presentations making use of Bayesian chronological models that we see each year at the Society for American Archaeology meeting and regional conferences in the Americas.
We hope this article brings a wider awareness to the noted issues and that journal editors and grant proposal reviewers familiarize themselves with these issues and the best practice methods provided in Bayliss (Reference Bayliss2015) and Buck and Meson (Reference Buck and Meson2015). We further recommend that anthropology departments and regional archaeological organizations offer more courses and other training activities that cover the fundamentals of Bayesian chronological modeling, because these methods will soon be considered part of the standard American archaeological tool kit.
It is especially important that archaeologists using these methods always consider that results with low precision are likely accurate and that preexisting beliefs, while sometimes very precise, might be inaccurate. Like Michczyñski's (Reference Michczyñski2007) conclusions regarding best practice for interpretations of probabilistic radiocarbon calibration, it is also important that 95% and 68% posterior probability ranges receive the most interpretative weight, even when the model results are largely imprecise. It is also important that archaeologists understand how calibration curve wiggles, such as the Hallstatt plateau and others, affect the precision of their modeled results. Poor awareness of calibration curve wiggles can lead to misinterpretations (Baillie Reference Baillie1991; Guilderson et al. Reference Guilderson, Reimer and Brown2005; Krus et al. Reference Krus, Cook and Hamilton2015). While imprecise modeling results are unfortunate, conclusions can still be drawn from those situations and can include discussions of the future scientific work to produce finer chronologies. Importantly, experiments with simulated radiocarbon data should be run in Bayesian chronological modeling software to precisely estimate the number of radiocarbon dates needed to produce precise and accurate models, which is a highly effective practice for determining the number of dates that are needed to overcome calibration curve wiggles.
Finally, it is important that American archaeologists understand that Bayesian chronological modeling is both a scientific and a theoretical revolution for our discipline (Bayliss Reference Bayliss2009). Future work in the Americas has the potential to improve our understandings of lived experiences, temporality, and cultural change derived probabilistically from posterior probabilities. When discussing the future of Bayesian chronological modeling, Buck and Meson (Reference Buck and Meson2015:577–579) emphasize that radiocarbon simulations have thus far been underused as a tool for improving the research designs of chronology-building programs and that these simulations are enormously useful for informing the selection of radiocarbon research designs. Similarly, at the 2017 Society for American Archaeology meeting, we noticed that most of the presented chronological modeling dealt with the analysis of legacy dates, with almost no discussion about how the Bayesian process will be used to inform the selection of new data.
We hope this article brings a greater awareness of how the Bayesian process can be used to shape all aspects of an archaeological research design, from the initial formation of a data collection strategy to the publication of results. While this article can be read as an introduction, we encourage readers to review the literature in the references cited section to learn more, and to contact established individuals who are publishing Bayesian models for practical advice.
Acknowledgments
We would like to thank Charles McNutt and Tim Rieth for reading drafts of this article and providing very useful comments and suggestions that have helped us to identify those areas where more detail might be necessary for new Bayesians. We are also indebted to the three anonymous reviewers whose comments were an immense help to refining the content and providing clarity to new Bayesians. Finally, we would like to give a special thanks to Águeda Lozano Medina for providing us with a Spanish translation of the abstract.
Data Availability Statement
No original data were presented in this article.
Supplemental Materials
Supplemental materials are linked to the online version of the manuscript, accessible via the SAA member login at https://doi.org//10.1017/aaq.2017.57.
Supplemental Text 1. The references for the papers in Figure 1 not cited in text.
Supplemental Text 2. Some references for the use of Bayesian statistics in the physical/natural sciences not cited in text.