Research Article
Principal polarizations of abelian surfaces over finite fields
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-4
-
- Article
-
- You have access
- Export citation
First Chern class and holomorphic tensor fields
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 5-11
-
- Article
-
- You have access
- Export citation
On the module structure of a p-extension over a
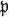 -adic number field
-adic number field
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 13-23
-
- Article
-
- You have access
- Export citation
On the integer ring of the compositum of algebraic number fields
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 25-31
-
- Article
-
- You have access
- Export citation
Completeness of two theories on ordered abelian groups and embedding relations
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 33-39
-
- Article
-
- You have access
- Export citation
On a conjecture of M. P. Murthy
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 41-45
-
- Article
-
- You have access
- Export citation
Moduli spaces of the stable vector bundles over abelian surfaces
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 47-60
-
- Article
-
- You have access
- Export citation
Some properties of weakly normal varieties*)
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 61-74
-
- Article
-
- You have access
- Export citation
On differential invariants of holomorphic projective curves
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 75-87
-
- Article
-
- You have access
- Export citation
Invariant subrings which are complete intersections, I: (Invariant subrings of finite Abelian groups)
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 89-98
-
- Article
-
- You have access
- Export citation
A contribution to the theory of formal meromorphic functions
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 99-106
-
- Article
-
- You have access
- Export citation
Hyperbolic affine hyperspheres
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 107-123
-
- Article
-
- You have access
- Export citation
Formal meromorphic functions and cohomology on an algebraic variety
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 125-135
-
- Article
-
- You have access
- Export citation
Finite arithmetic subgroups of GLn, II
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 137-143
-
- Article
-
- You have access
- Export citation
Weil type representations and automorphic forms
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 145-166
-
- Article
-
- You have access
- Export citation
Some examples of integral definite quaternary quadratic forms with prime discriminant
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 167-175
-
- Article
-
- You have access
- Export citation
On the composition series of principal series representations of a three-fold covering group of SL(2, K)1)
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 177-196
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 77 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f6
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 77 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation

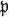 -adic number field
-adic number field
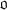 be the ring of all integers in
be the ring of all integers in 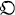 of all integers in
of all integers in 
 and if
and if 