Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-19T16:45:55.354Z Has data issue: false hasContentIssue false
  • English
  • Français

On the supports of Gauss measures on algebraic groups

Published online by Cambridge University Press:  24 October 2008

M. McCrudden
M. McCrudden
Affiliation:
Department of Mathematics, University of Manchester
Get access Rights & Permissions [Opens in a new window]

Extract

For any locally compact topological group G let M(G) denote the topological semigroup of all probability (Borel) measures on G, furnished with the weak topology and with convolution as the multiplication. A Gauss semigroup on G is a homomorphism t→ μt of the strictly positive reals 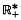(under addition) into M(G) such that

(i) no μt is a point mesaure,

(ii) for each neighbourhood V of 1 in G we have

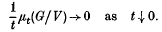
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 96 , Issue 3 , November 1984 , pp. 437 - 445
Copyright
Copyright © Cambridge Philosophical Society 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Heyer, H.. Probability measures on locally compact groups. Ergeb. Math. Grenzgeb. 94 (Springer-Verlag, 1977).CrossRefGoogle Scholar
[2]Humphreys, J. E.. Linear Algebraic Groups. Graduate Texts in Mathematics 21 (Springer-Verlag, 1975).CrossRefGoogle Scholar
[3]McCrudden, M.. On the supports of absolutely continuous Gauss measures on connected Lie groups. Monatsh. Math, (to appear).Google Scholar
[4]McCrudden, M. and Wood, R. M.. On the support of absolutely continuous Gauss measures on SL (2, it). In Probabilities on Groups, Proc. Conf. Oberwolfach, April 1983, Lecture Notes in Mathematics, vol. 1064 (Springer-Verlag, 1984).Google Scholar
[5]Siebert, E.. Absolute continuity, singularity and supports of Gauss semigroups on a Lie group. Monatsh. Math. 93 (1982), 239–253.CrossRefGoogle Scholar
[6]Springer, T. A.. Linear Algebraic Groups. Progress in Mathematics, 9 (Birkhauser, 1981).Google Scholar
[7]Yamabe, H.. On an arcwise connected subgroup of a Lie group. Osaka J. Math. 2 (1950), 13–14.Google Scholar