Research Article
3-transpositions in infinite groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 371-377
-
- Article
- Export citation
Soluble-by-periodic skew linear groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 379-389
-
- Article
- Export citation
Unsound ordinals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 391-411
-
- Article
- Export citation
A new proof for the residual set dimension of the apollonian packing
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 413-423
-
- Article
- Export citation
Generic 1-parameter families of caustics by reflexion in the plane
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 425-432
-
- Article
- Export citation
The existence of sextactic points
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 433-436
-
- Article
- Export citation
On the supports of Gauss measures on algebraic groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 437-445
-
- Article
- Export citation
Badly ordered orbits of circle maps
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 447-451
-
- Article
- Export citation
Holomorphic and abstract inducing
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 453-468
-
- Article
- Export citation
A note on unknotting number
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 469-471
-
- Article
- Export citation
On invariant knots
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 473-475
-
- Article
- Export citation
Best L∞-approximation of measurable, vector-valued functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 477-481
-
- Article
- Export citation
Complex strict and uniform convexity and hyponormal operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 483-493
-
- Article
- Export citation
On ∧-Mackey convergence in locally convex spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 495-500
-
- Article
- Export citation
Mean values and classes of harmonic functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 501-505
-
- Article
- Export citation
On the limit distributions of lightly trimmed sums
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 507-516
-
- Article
- Export citation
Limit theorems for sums of general functions of m-spacings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 517-532
-
- Article
- Export citation
Uniform ε-independence and the convergence in distribution of randomly indexed sequences
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 533-542
-
- Article
- Export citation
A classification theorem for planar distributions based on the shape statistics of independent tetrads
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 543-547
-
- Article
- Export citation
Boundary conditions and reducibility of differential operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 549-553
-
- Article
- Export citation

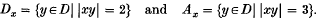
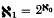 then the least unsound ordinal is exactly
then the least unsound ordinal is exactly 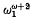 but that if ω
but that if ω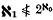 the least unsound ordinal, assuming one exists, is at least
the least unsound ordinal, assuming one exists, is at least 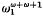 . Arguments due to Kechris and Woodin are presented showing that under the axiom of determinacy there is an unsound ordinal less than ω
. Arguments due to Kechris and Woodin are presented showing that under the axiom of determinacy there is an unsound ordinal less than ω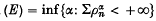 proved by Boyd
proved by Boyd 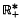 (under addition) into
(under addition) into 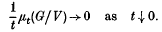
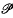 ,μ) be a probability space, and let
,μ) be a probability space, and let 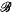 be a sub-sigma-algebra of
be a sub-sigma-algebra of 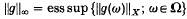
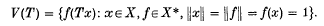
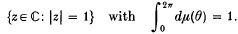

 , | ξ | =
, | ξ | = 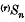 be
be 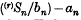 coverages in distribution to
coverages in distribution to