Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-17T16:42:14.601Z Has data issue: false hasContentIssue false
  • English
  • Français

Homological finiteness conditions for modules over strongly group-graded rings

Published online by Cambridge University Press:  24 October 2008

Jonathan Cornick  and
Peter H. Kropholler
Jonathan Cornick
Affiliation:
Centre de Recerca Matematica, Institut d'estudis Catalans, Apartat 50, E 08193 Bellaterra, Spain
Peter H. Kropholler
Affiliation:
School of Mathematical Sciences, Queen Mary and Westfield College, Mile End Road, London E1 4NS
Get access Rights & Permissions [Opens in a new window]

Extract

Throughout this paper, k denotes a commutative ring. We will develop a theory of homological finiteness conditions for modules over certain graded k-algebras which generalizes known theory for group algebras. The simplest of our results, Theorem A below, generalizes certain results of Aljadeff and Yi on crossed products of polycyclic-by-finite groups (cf. [1, 11]), but also applies to many other crossed products in cases where little was previously known. Before stating the results, we recall definitions of graded and strongly graded rings. Let G be a monoid. Naively, a G-graded k-algebra is a k-algebra R which admits a k-module decomposition,

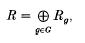
in such a way that Rg Rh ⊆ for all g, h ∈ G. If R is a G-graded k-algebra and X is any subset of G, then we write Rx for the k-submodule of R supported on X; that is

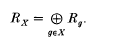
Note that if H is a submonoid of G then RH is a subalgebra of R.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 120 , Issue 1 , July 1996 , pp. 43 - 54
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aljadeff, E.. Serre's extension theorem for crossed products. J. London Math. Soc. 44 (1991), 47–54.CrossRefGoogle Scholar
[2]Benson, D. J. and Carlson, J.. Products in negative cohomology. J. Pure Appl. Algebra 82 (1992), 107–130.CrossRefGoogle Scholar
[3]Brown, K. S.. Cohomology of groups (Springer, Berlin, 1982).CrossRefGoogle Scholar
[4]Cornick, J. and Kropholler, P. H.. Homological finiteness conditions for modules over group rings, preprint, QMW, University of London (1994).Google Scholar
[5]Dade, E. C.. Group graded rings and modules. Math. Z. 174 (1980), 241–262.CrossRefGoogle Scholar
[6]Goichot, F.. Homologie de Tate-Vogel équivariante. J. Pure Appl. Algebra 82 (1992), 39–64.CrossRefGoogle Scholar
[7]Kaplansky, I.. Fields and rings 2nd ed. (University of Chicago Press, 1972).Google Scholar
[8]Kropholler, P. H.. On groups of type, FP∞. J. Pure Appl. Algebra 90 (1993), 55–67.CrossRefGoogle Scholar
[9]Kropholler, P. H. and Talelli, O.. On a property of fundamental groups of graphs of finite groups. J. Pure Appl. Algebra 74 (1991), 57–59.CrossRefGoogle Scholar
[10]Mislin, G.. Tate cohomology for arbitrary groups via satellites. Topology and its Applications 56 (1994), 293–300.CrossRefGoogle Scholar
[11]Yi, Z.. Homological dimension of skew group rings and crossed products. J. Algebra 164 (1994), 101–123.CrossRefGoogle Scholar