Research Article
On a class of aperiodic sum-free sets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 01-05
-
- Article
- Export citation
Countable partitions of Euclidean space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 07-12
-
- Article
- Export citation
The elliptic Mahler measure
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 13-25
-
- Article
- Export citation
Representation of an element in SL(2,
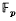 ,) as a short word in two generators
,) as a short word in two generators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 27-29
-
- Article
- Export citation
On the lengths of Koszul homology modules and generalized fractions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 31-42
-
- Article
- Export citation
Homological finiteness conditions for modules over strongly group-graded rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 43-54
-
- Article
- Export citation
Horizontal partitions and Kleshchev's algorithm
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 55-60
-
- Article
- Export citation
Hyperkähler metrics associated to compact Lie groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 61-69
-
- Article
- Export citation
A characterization of generalized Hughes complexes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 71-85
-
- Article
- Export citation
Localization of modular lattices, Krull dimension, and the Hopkins-Levitzki theorem (I)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 87-101
-
- Article
- Export citation
Invariant theory and Steenrod operations – maps between rings of invariants
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 103-116
-
- Article
- Export citation
Continuity of functions operating on characteristic functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 117-125
-
- Article
- Export citation
Dehn surgery and essential annuli*
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 127-146
-
- Article
- Export citation
The Haagerup invariant for tensor products of operator spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 147-153
-
- Article
- Export citation
Compact tripotents in bi-dual JB*-triples1
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 155-173
-
- Article
- Export citation
Converses for the Dodds–Fremlin and Kalton–Saab theorems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 175-179
-
- Article
- Export citation
Limits of commutative triangular systems on real and p-adic groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 181-192
-
- Article
- Export citation
Front matter
PSP volume 120 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 120 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

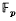 ,) as a short word in two generators
,) as a short word in two generators
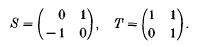
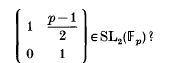
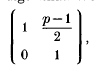
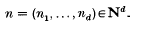
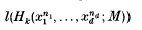
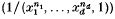 in
in 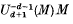 a polynomial in
a polynomial in 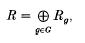
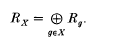
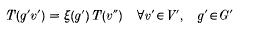
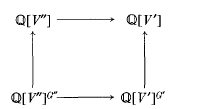
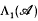 and
and 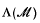 for
for  and von Neumann algebras
and von Neumann algebras 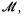 , based on appropriate forms of the completely bounded approximation property defined below. These definitions have obvious extensions to operator spaces and dual operator spaces respectively, and in [16] we established the multiplicativity of A on the ultraweakly closed spatial tensor product of two dual operator spaces
, based on appropriate forms of the completely bounded approximation property defined below. These definitions have obvious extensions to operator spaces and dual operator spaces respectively, and in [16] we established the multiplicativity of A on the ultraweakly closed spatial tensor product of two dual operator spaces 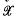 and
and 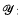 :
: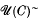 consisting of the partially ordered set
consisting of the partially ordered set 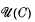 of tripotents in a JBW*-triple
of tripotents in a JBW*-triple 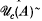 of
of 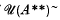 consisting of the set
consisting of the set 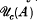 of tripotents
of tripotents  where B is a Banach space such that
where B is a Banach space such that