Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
NILSEN, MAY M.
and
SMITH, ROGER R.
2001.
APPROXIMATION PROPERTIES FOR CROSSED PRODUCTS BY ACTIONS AND COACTIONS.
International Journal of Mathematics,
Vol. 12,
Issue. 05,
p.
595.
Meng, Qing
2023.
Exel’s approximation property and the CBAP of crossed products.
Filomat,
Vol. 37,
Issue. 18,
p.
5943.




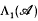 and
and 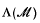 for
for 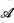 and von Neumann algebras
and von Neumann algebras 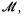 , based on appropriate forms of the completely bounded approximation property defined below. These definitions have obvious extensions to operator spaces and dual operator spaces respectively, and in [16] we established the multiplicativity of A on the ultraweakly closed spatial tensor product of two dual operator spaces
, based on appropriate forms of the completely bounded approximation property defined below. These definitions have obvious extensions to operator spaces and dual operator spaces respectively, and in [16] we established the multiplicativity of A on the ultraweakly closed spatial tensor product of two dual operator spaces 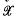 and
and 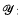 :
: