Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-17T18:13:50.013Z Has data issue: false hasContentIssue false
  • English
  • Français

On non-wellfounded iterations of the perfect set forcing

Published online by Cambridge University Press:  12 March 2014

Vladimir Kanovei
Vladimir Kanovei*
Affiliation:
Moscow Center of Continuous Mathematical Education, Bolshaya Cherkizovskaya St, 9, Kor. 4 KV. 94, Moscow 107392, Russia E-mail: kanovei@math.uni-wuppertal.de, kanovei@mech.math.msu.su
Get access Rights & Permissions [Opens in a new window]

Abstract

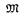We prove that if I is a partially ordered set in a countable transitive model of ZFC then 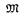can be extended by a generic sequence of reals ai, i ∈ I, such that 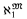is preserved and every ai is Sacks generic over 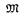[〈aj: j < i〉]. The structure of the degrees of -constructibility of reals in the extension is investigated.

As applications of the methods involved, we define a cardinal invariant to distinguish product and iterated Sacks extensions, and give a short proof of a theorem (by Budinas) that in ω2-iterated Sacks extension of L the Burgess selection principle for analytic equivalence relations holds.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 64 , Issue 2 , June 1999 , pp. 551 - 574
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Baumgartner, J. E. and Laver, R., Iterated perfect set forcing, Annals of Mathematical Logic, vol. 17 (1979), pp. 271–288.CrossRefGoogle Scholar
[2] Budinas, B. I., The selection principle for analytic equivalence relations does not imply the existence of a total A2 wellordering of the continuum, Jatematicheskiĭ Sbornik, vol. 120 (1983), pp. 164–179.Google Scholar
[3] Burgess, J., A selection principle for equivalence relations, Michigan Mathematical Journal, vol. 24 (1977), pp. 65–76.CrossRefGoogle Scholar
[4] Groszek, M., Applications of iterated perfect set forcing, Annals of Pure and Applied Logic, vol. 39 (1988), pp. 19–53.CrossRefGoogle Scholar
[5] Groszek, M., ω1* as an initial segment of the c-degrees, this Journal, vol. 59 (1994), pp. 956–976.Google Scholar
[6] Groszek, M. and Jech, T., Generalized iteration of forcing, Transactions of the American Mathematical Society, vol. 324 (1991), pp. 1–26.CrossRefGoogle Scholar
[7] Sacks, G. E., Forcing with perfect closed sets, Axiomatic set theory, Part 1, Proceedings of Symposia in Pure Mathematics, no. 13, American Mathematical Society, Providence, 1971, pp. 331–355.Google Scholar
[8] Solovay, R. M. and Tennenbaum, S., Iterated Cohen extensions and Souslin's problem, Annals of Mathematics, vol. 94 (1971), pp. 201–245.CrossRefGoogle Scholar