Research Article
Anti-admissible sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 407-435
-
- Article
- Export citation
Some remarks on the partition calculus of ordinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 436-442
-
- Article
- Export citation
The largest countable inductive set is a mouse set
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 443-459
-
- Article
- Export citation
A jump operator for subrecursion theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 460-468
-
- Article
- Export citation
Countable filters on ω
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 469-478
-
- Article
- Export citation
Cut-elimination for simple type theory with an axiom of choice
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 479-485
-
- Article
- Export citation
Frege's theorem in a constructive setting
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 486-488
-
- Article
- Export citation
Generalized cohesiveness
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 489-516
-
- Article
- Export citation
Explicit mathematics with the monotone fixed point principle. II: Models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 517-550
-
- Article
- Export citation
On non-wellfounded iterations of the perfect set forcing
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 551-574
-
- Article
- Export citation
Universal classes of simple relation algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 575-589
-
- Article
- Export citation
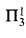 sets and
sets and 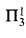 singletons
singletons
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 590-616
-
- Article
- Export citation
Tensor product and theories of modules
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 617-628
-
- Article
- Export citation
Prime e.c. commutative rings in characteristic n ≥ 2
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 629-633
-
- Article
- Export citation
Constructing strongly equivalent nonisomorphic models for unsuperstable theories, Part C
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 634-642
-
- Article
- Export citation
The cupping theorem in R/M
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 643-650
-
- Article
- Export citation
A decidable variety that is finitely undecidable
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 651-677
-
- Article
- Export citation
Transfering saturation, the finite cover property, and stability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 678-684
-
- Article
- Export citation
Common knowledge logic and game logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 685-700
-
- Article
- Export citation
Unions of rectifiable curves in Euclidean space and the covering number of the meagre ideal
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 701-726
-
- Article
- Export citation



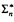 real is in
real is in 
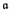 (
(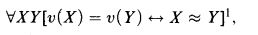
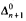
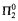 2-cohesive set. We show that the
2-cohesive set. We show that the 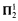 comprehension. [14] showed that T
comprehension. [14] showed that T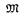 of ZFC then
of ZFC then 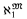 is preserved and every
is preserved and every 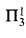 sets and
sets and