Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-19T10:51:34.145Z Has data issue: false hasContentIssue false
  • English
  • Français

On characterizing Spector classes

Published online by Cambridge University Press:  12 March 2014

Leo A. Harrington  and
Alexander. S. Kechris
Leo A. Harrington
Affiliation:
State University of New Yorkat Buffalo, Amherst, New York 14226
Alexander. S. Kechris
Affiliation:
Massachusetts Institute of Technology, Cambridge, Massachusetts 02139
Get access Rights & Permissions [Opens in a new window]

Extract

We study in this paper characterizations of various interesting classes of relations arising in recursion theory. We first determine which Spector classes on the structure of arithmetic arise from recursion in normal type 2 objects, giving a partial answer to a problem raised by Moschovakis [8], where the notion of Spector class was first essentially introduced. Our result here was independently discovered by S. G. Simpson (see [3]). We conclude our study of Spector classes by examining two simple relations between them and a natural hierarchy to which they give rise.

The second part of our paper is concerned with finding structural characterizations of classes of relations on the reals in the spirit of Moschovakis [7]. Our main result provides a single abstract characterization for the class of 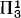relations on the reals and the 2-envelope of 3E, the first one being valid if projective determinacy is true, the second if V = L is true.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 40 , Issue 1 , March 1975 , pp. 19 - 24
Copyright
Copyright © Association for Symbolic Logic 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Addison, J. W. and Moschovakis, Y. N., Some consequences of the axiom of definable determinateness, Proceedings of the National Academy of Sciences, U.S.A., vol. 59 (1968), pp. 708–712.CrossRefGoogle ScholarPubMed
[2]Harrington, L., Contributions to recursion theory on higher types, Ph.D. Thesis, M.I.T., Cambridge, Massachusetts, 1973.Google Scholar
[3]Harrington, L., Kechris, A. S. and Simpson, S. G., 1-envelopes of type 2 objects, Notices of the American Mathematical Society, vol. 20 (1973), A–587.Google Scholar
[4]Kechris, A. S., The theory of countable analytical sets, Transactions of the American Mathematical Society (to appear).Google Scholar
[5]Martin, D. A., The axiom of determinateness and reduction principles in the analytical hierarchy, Bulletin of the American Mathematical Society, vol. 74 (1968), pp. 687–689.CrossRefGoogle Scholar
[6]Moschovakis, Y. N., Elementary induction on abstract structures, North-Holland, Amsterdam, 1974.Google Scholar
[7]Moschovakis, Y. N., Structural characterizations of classes of relations, Generalized recursion theory (Oslo, 1972) (Fenstad, J. and Hinman, P., Editors), North-Holland, Amsterdam, 1973.Google Scholar
[8]Moschovakis, Y. N., Axioms for computation theories—first draft, Logic Colloquium '69, North-Holland, Amsterdam, 1971, pp. 199–255.CrossRefGoogle Scholar
[9]Sacks, G. E., F-recursiveness, Logic Colloquium '69, North-Holland, Amsterdam, 1971, pp. 289–303.CrossRefGoogle Scholar