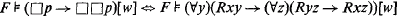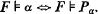Research Article
A new look at the interpolation problem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-13
-
- Article
- Export citation
Lawvere's basic theory of the category of categories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 14-18
-
- Article
- Export citation
On characterizing Spector classes
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 19-24
-
- Article
- Export citation
Weak liberated versions of T and S41
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 25-30
-
- Article
- Export citation
A counterexample in the theory of model companions1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 31-34
-
- Article
- Export citation
First-order definability in modal logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 35-40
-
- Article
- Export citation
On models of arithmetic—Answers to two problems raised by H. Gaifman
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 41-47
-
- Article
- Export citation
A large power set axiom
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 48-54
-
- Article
- Export citation
A note on modal formulae and relational properties
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 55-58
-
- Article
- Export citation
Descending sequences of degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 59-61
-
- Article
- Export citation
Skolem reduction classes
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 62-68
-
- Article
- Export citation
The word problem for free fields: a correction and an addendum
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 69-74
-
- Article
- Export citation
On partitions into stationary sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 75-80
-
- Article
- Export citation
Reviews
Corrado Böhm and Wolf Gross. Introduction to the CUCH. Automata theory, edited by E. R. Caianiello, Academic Press, New York and London1966, pp. 35–65. Reprinted in Pubblicazioni dell'Istituto Nazionale per le Applicazioni del Calcolo, ser. 11 no. 669, Rome 1966. - C. Böhm. The CUCH as a formal and description language. Formal language description languages for computer programming, Proceedings of the IFIP Working Conference on Formal Language Description Languages, edited by T. B. SteelJr., North-Holland Publishing Company, Amsterdam1966, pp. 179–197.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 81-83
-
- Article
- Export citation
J. W. de Barker. Recursive procedures. Mathematical Centre tracts, no. 24, Mathematisch Centrum, Amsterdam1971, viii + 108 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 83
-
- Article
- Export citation
Oliver Aberth. Analysis in the computable number field. Journal of the Association for Computing Machinery, vol. 15 (1968), pp. 275–299.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 84
-
- Article
- Export citation
Oliver Aberth. A chain of inclusion relations in computable analysis. Proceedings of the American Mathematical Society, vol. 22 (1969), pp. 539–548.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 84
-
- Article
- Export citation
Oliver Aberth. The concept of effective method applied to computational problems of linear algebra. Journal of computer and system sciences, vol. 5 (1971), pp. 17–25.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 84
-
- Article
- Export citation
Oliver Aberth. Computable analysis and differential equations. Intuitionism and proof theory, Proceedings of the summer conference at Buffalo N.Y. 1968, edited by A. Kino, J. Myhill, and R. E. Vesley, Studies in logic and the foundations of mathematics, North-Holland Publishing Company, Amsterdam and London1970, pp. 47–52.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 84
-
- Article
- Export citation
Oliver Aberth. The failure in computable analysis of a classical existence theorem for differential equations. Proceedings of the American Mathematical Society, vol. 30 (1971), pp. 151–156.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 85
-
- Article
- Export citation



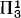 relations on the reals and the 2-envelope of
relations on the reals and the 2-envelope of