No CrossRef data available.
Article contents
A downward Löwenheim-Skolem theorem for infinitary theories which have the unsuperstability property
Published online by Cambridge University Press: 12 March 2014
Abstract
We present a downward Löwenheim-Skolem theorem which transfers downward formulas from L∞,ω
to 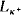 , ω. The simplest instance is:
, ω. The simplest instance is:
Theorem 1. Let λ > κ be infinite cardinals, and let L be a similarity type of cardinality κ at most. For every L-structure M of cardinality λ and every X ⊆ M there exists a model N ≺ M containing the set X of power ∣X∣ · κ such that for every pair of finite sequences a, b ∈ N
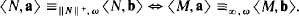
The following theorem is an application:
Theorem 2. Let λ<κ, T ∈ 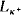 , ω, and suppose χ is a Ramsey cardinal greater than λ. If T has the (χ,
, ω, and suppose χ is a Ramsey cardinal greater than λ. If T has the (χ, 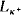 , ω)-unsuperstability property, then T has the (χ,
, ω)-unsuperstability property, then T has the (χ, 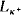 , ω)-unsuperstability property.
, ω)-unsuperstability property.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1988
Footnotes
I would like to thank John Baldwin for asking me a question which is the reason why I wrote this paper, and for his valuable remarks on the first draft. This research was partially supported by NSF grant DMS-8603167.


